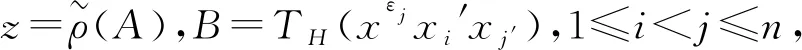无限维模李超代数H和SHO的阶化模

张华雁,徐晓宁

(1.辽宁大学 数学院，沈阳 110036；2.聊城颐中外国语学校，山东 聊城 252000)

0 引言

李代数是于19世纪由挪威数学家M.S.Lie创立李群的时候引进的数学概念。1974年Wess和Zumino为了建立物理学中相对的费米子和玻色子的统一理论而提出了超对称性，将普通时空满足的Poincare李代数(即非齐次Lorentz代数)扩充为超Poincare李代数。自此李超代数的研究便有了迅速发展。根据基域的不同，将李超代数分为特征为零的域上的李超代数和素特征域上的李超代数，即非模李超代数和模李超代数。

文献[1]研究了δ-李三系的广义导子。V.G.Kac在1977年完成了特征为零的域上有限维单李超代数的分类[2]。1998年，V.G.Kac将特征为零的域上无限维单的线性紧致李超代数进行了分类[3]。目前非模李超代数的研究已经取得了系统的研究结果[2-8]，但是模李超代数的研究结果尚少。1992年D.Leites，Y.Kochetkov和V.M.Petrogradski开始探究模李超代数[9-10]。Petrogradski还引入了(p,2p)-结构，限制型李超代数由此产生。1996年Farnsteiner又对限制型李超代数及Frobenius扩张做了进一步研究[11-12]。1997年，张永正构造出了4类Cartan型模李超代数W，S，H和K[13]。接着Cartan型模李超代数HO，SHO，KO和SKO也被构造出来[14-17]。同时，这八类单模李超代数的表示的课题应运而生[18-22,24-25]，本研究主要探究无限维Cartan型模李超代数H，SHO的阶化模。

1 基本概念

在本研究中总设基域F的特征p>2，为非负整数集，m表示中任意m个整数组成的集合，Z2表示整数模2的剩余类环。设U(m)是具有生成元集{xα|α∈m}的F上的除幂代数。用Λ(n)表示具有n个不定元xm+1,…，xs的外代数，其中s=m+n。令Λ(m,n)=U(m)⊗Λ(n)。显然，U(m)的平凡Z2-阶化与Λ(n)的自然Z2-阶化诱导了Λ(m,n)的一个Z2-阶化，使得Λ(m,n)成为一个超代数。设f∈U(m)，g∈Λ(n)，简记Λ(m,n)中的元素f⊗g为fg。于是在Λ(m,n)上的乘法运算可定义为

Di(x(α)xu)={x(α-ei)xu(i∈Y0),

x(α)·(∂xu/∂xi) (i∈Y1),

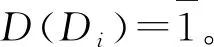
[aDi,dDj]=aDi(b)Dj-(-1)d(dDi)d(bDj)bDj(a)Di，

其中：a,b∈Λ(m,n)；i,j∈Y；Di,Dj∈DerΛ(m,n)。

设d=(d1,…,dm)∈m，记中元素xm+1,…,xm+n用X表示，Xi1,…，ir表示X删去因子xi1,…,xir所得到的元素。令θ=〈i1,…，ir〉，xθ=xi1…xir。首先定义Λ(m,n)上的一个Z-阶化为其中Λ(m,n)i=spanF{xαxu‖α|+|u|=i,α∈m,u∈B(n)}，同时这个Z-阶化可以诱导出W(m,n)的一个Z-阶化：其中

2 混合积及H的阶化模

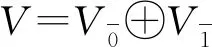
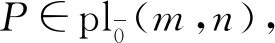
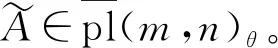
由于d(Eij)=τ(k)+τ(j)，所以

[Ekj,Eil]=Ekl-(-1)τ(k)+τ(j))(τ(i)+τ(l))Eij。

引理2.1[23]159若A∈W(m,n)θ，B∈W(m,n)μ，θ,μ∈Z2，设C=[A,B]，则有

下面介绍李超代数中的伸张。

[a⊗x,b⊗y]=(-1)d(x)d(b)ab⊗[x,y],a,b∈Λ(m,n),x,y∈pl(m,n),

(A⊗1)(a⊗x)=A(a)⊗x,a∈Λ(m,n),x∈pl(m,n),

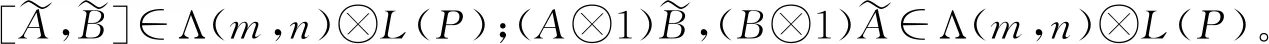
因此[A,B]∈Ω，则Ω是W(m,n)的子代数。仿照文献[23]我们称Ω为在W(m,n)中的P-伸张。当P为单位阵时我们称Ω为L在W(m,n)中的伸张。

显然W(m,n)就是pl(m,n)在W(m,n)中的伸张。

设ρ是pl(m,n)的子代数L(P)在Z2-阶化空间V上的表示，则将ρ扩充成李超代数Λ(m,n)⊗L(P)在Λ(m,n)⊗V空间上的表示ρ1。

ρ1(a⊗x)(b⊗v)=(-1)d(x)d(b)ab⊗ρ(x)(v) (a,b∈Λ(m,n),x∈L,v∈V)。

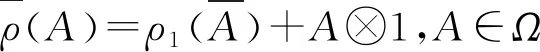
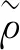
定义李超代数H(m,n)，要求m为偶数，设m=2k，令

定义线性映射DH∶Λ(m,n)→W(m,n)使得对∀f∈hg(Λ(m,n))有

其中：

fi=σ(i′)(-1)τ(i′)d(f)Di′(f),∀f∈Y。

(1)

显然，d(fi)=d(f)+τ(i′),∀i∈Y，由式(1)可得

Di(fj′)=σ(i)σ(j)(-1)τ(i)τ(j)+(τ(i)+(τ(j))θDi(fi′)=0,

其中i,j∈Y。令H(m,n)=spanF{DH(f)|f∈hgΛ(m,n)}。可证得H(m,n)是W(m,n)的无限维子代数。

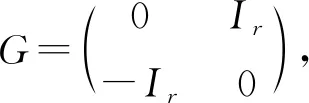
则I是pl(m,n)的一个子代数。

置

Y1={Eij′-σ(i)σ(j)Eit′|1≤i≤j≤m}，Y2={Eij+Eji|m+1≤i≤j≤s}，

Y3={Eij-σ(i)Eji′|1≤i≤m,m+1≤j≤s}，

引理2.4[23]164对于i,j∈Y,定义ψ(DH(xixj))=σ(j)(-1)τ(j)Tij′是一个线性算子。则ψ是H(m,n)0到L的李超代数同构。

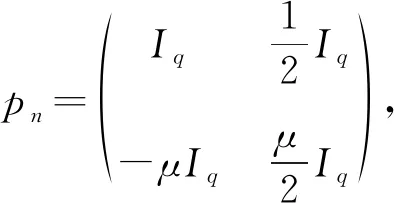
引理2.5[23]165H(m,n)是L在W(m,n)上的P-伸张。

由引理2.5可得下述推论：

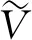
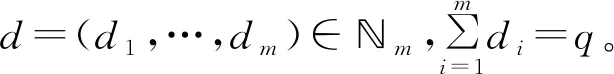
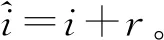
它的素根系为

L={Λ1-Λ2},…，(Λq-1-Λq),(Λq-1+Λq),(Λn+1-Λn+2),…，(Λn+r-1-Λn+r),(Λn+r-Λ1},

其中:Λi(i=1,2,…，q,n+1,…，n+r)是〈Ell,…，Ess〉的线性函数，使得Λi(Ejj)=δij。其基本权为

(2)

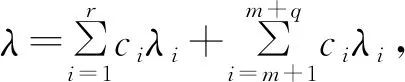
令E1=E1t-Et′1′，E2=E1t′-Et1′，E3=E1t′-Et′1，E4=E1t-Et′1′，通过计算可得以下等式

(3)

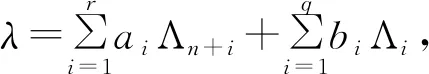
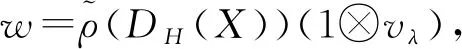
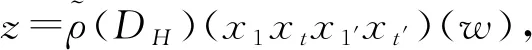
z=(-1)n2X⊗ρ(P(E1t-Et1)P-1)ρ(P(E1′t′-Et′1′)P-1)vλ-
(-1)n2X⊗ρ(P(E11′-E1′1)P-1)ρ(P(Et′t′-Et′t′)P-1)vλ+
(-1)n2X⊗ρ(P(E1t′-Et′1)P-1)ρ(P(Et1′-E1′t)P-1)vλ。

(4)

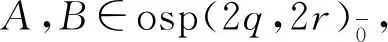
(-1)n2X⊗(μ2b1btvλ)=(-1)n2bt(1+b1)X⊗vλ。

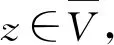
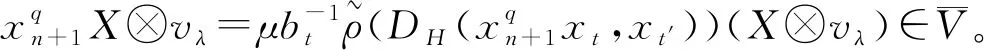
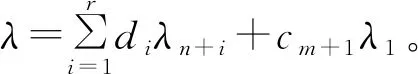
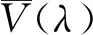
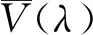
(5)

首先证明

(6)

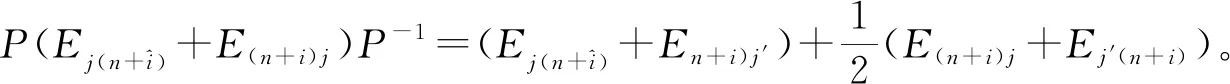
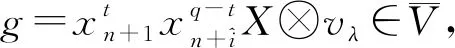
所以有

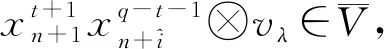
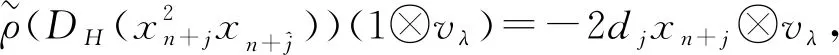
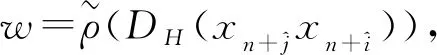
由以上定理2.8和定理2.9可得以下定理。

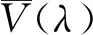
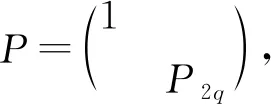
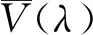
3 SHO的阶化模

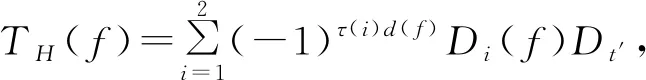
HO(n,n)={TH(F)|f∈Λ(n,n)}，

这里α∈Z2，可得HO(m,n)是一个单李超代数。令HO(m,n)i=spanF{xαxu‖α|+|u|=i+2,α∈n,u∈β(n)}，则是一个Z-阶化的李超代数。

对i∈Y，定义线性算子div(f(Di))=(-1)τ(i)d(f)Di(f)，这里fDi∈W(m,n)，则div是W(n,n)的超导子。置

S′(n,n)={fDi∈W(n,n)|div(fDi)=0}。

则S′(n,n)是W(n,n)是的一个Z-阶化超导算子，并且其导代数是一个单李超代数。定义

SHO′(n,n)=HO(n,n)∩S′(n,n),

SHO(n,n)=[SHO′(n,n),SHO′(n,n)]。

SHO(n,n)i=HO(n,n)i∩SHO(n,n)。

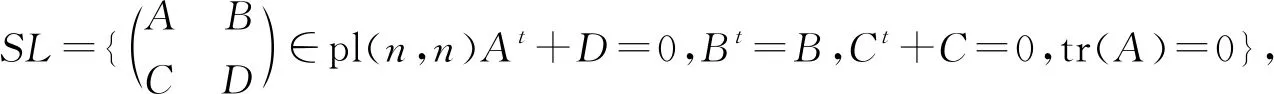
令

SJ1={Eij-Ej′i′,Eii-Ei′i′-Ell+El′l′|i,j,l∈Y0,i≠j}，

SJ2={Eij+Ej′i′|i∈Y0,j∈Y1},SJ3={Eij-Ej′i′|i∈Y1,j∈Y0},

则SJ1∪SJ2∪SJ3是SL的基。

引理2.13 对任意的i,j∈Y，定义线性映射ψ(xiDj)=Eij。则ψ是SHO0到SL的同构映射。

推论2.14HO∩S′是SL在W上的P-伸张。

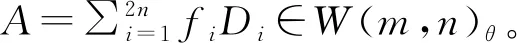
而Eij-(-1)τ(i)τ(j′)+τ(j′)Eji′∈SL,故有

因为Eij′∉SL，因此有

对i=j(其中i，j∈Y0),有Eij′∈SL。则-Di(fi′)+(-1)τ(i)Di(fi′)=-Di(fi′)+Di(fi′)=0。综上可得，Ω=SHO′。

易知SL的标准Cartan子代数为

SH=spanF{Eii-Ei′i′-Enn+En′n′|i∈Y0}，

SL的素根系为

SL={(Λi-Λi+1),(Λi+Λi+1)-(Λk+Λk+1),-(Λk-Λk+1)}，

其中：1≤i≤n-1，n+1≤k≤2n-1，Λi(Ejj)=δij。其基本权为

令A=TH(x2εiXi′)，则