基于UCT搜索算法的点格棋博弈系统研究
2021-05-11朱良双王静文李媛
朱良双 王静文 李媛
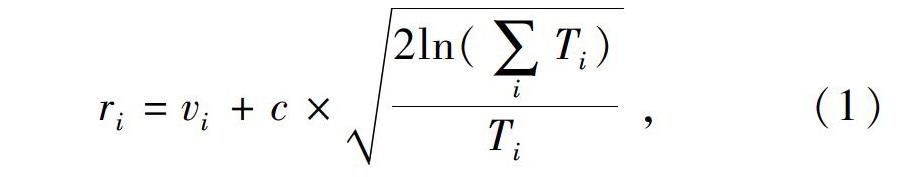
摘要:蒙特卡罗树搜索(MCTS)在许多完备的信息双人游戏中获得成功。本文给出了UCT(UpperConfidenceBoundApplytoTree)算法結合了UCB公式和蒙特卡洛树搜索算法,同时与局面评估相结合,根据点格棋长链和环的特点对算法进行了优化。有利于更快更准地找到当前局面的最优解。
关键词:UCT算法;估值函数;点格棋
【Abstract】MonteCarlotreesearch(MCTS)hasbeensuccessfulinmanyperfectinformationgames.Inthispaper,UCT(UpperConfidenceBoundApplytoTree)algorithmisproposed,whichcombinesUCBformulaandMonteCarlotreesearchalgorithm.Meanwhilecombinedwithsituationassessment,theselectionofnodesforevaluationbyUCBalgorithmisconducivetofindtheoptimalsolutionofthecurrentsituationfasterandmoreaccurately.
【Keywords】UCTalgorithm;evaluationfunction;DotsandBoxes
作者简介:朱良双(1999-),男,本科生,主要研究方向:计算机博弈;王静文(1965-),男,工程师,主要研究方向:人工智能和信息安全;李媛(1976-),女,博士后,教授,主要研究方向:人工智能和随机过程。
0引言
众所周知,点格棋是由数学家爱德华·卢卡斯提出的一种只需要在纸上就可以进行的游戏。与一般的传统游戏不同,点格棋的玩法是通过点与点之间的边来占领格子,再根据所占领区域大小来判定胜负,是一种将图论、数学等知识结合在一起的游戏。
在国内,自2011年起在全国大学生计算机博弈竞赛已将该项目作为竞赛项目之一,随着国内外各类机器博弈赛事的陆续举办,对于点格棋搜索算法的研究受到了越来越多的爱好者关注,在2020年的全国大学生计算机大赛中,点格棋的参赛队伍已达到27支,为历年最多。
1点格棋简介
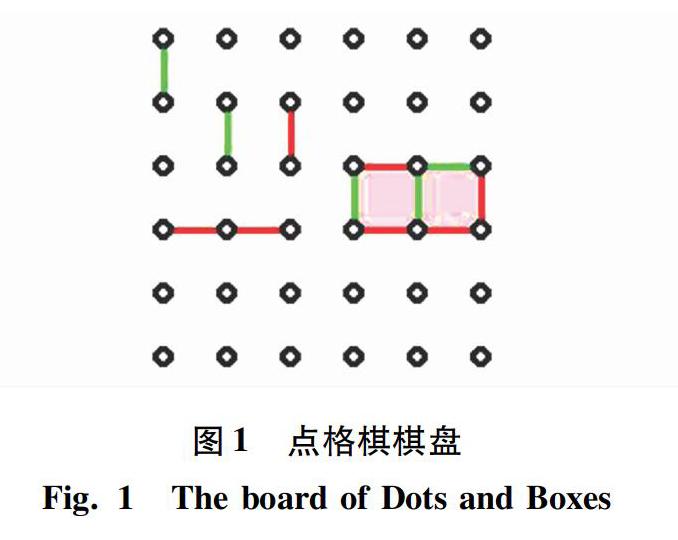
点格棋的棋盘大小可以根据情况进行设置,典型的点格棋棋盘由6×6的点围成的5×5的格子,如图1所示。
图1中,棋盘中共60条边,格子数为25,由于比赛胜负是按照双方所占格子数来确定,格子数为奇数时可以避免出现平局情况。
点格棋的基本规则如下:
(1)双方轮流在水平或竖直方向的相邻两点之间下棋。
(2)当每个格子四条边被占满时,这个格子被最后一条边的捕获者所占领。
(3)当一方占有格子后,必须在下一条边,直至不再占有格子。
(4)当格子全部围成后,根据格子归属统计得分,捕获格子多的一方获胜。
2搜索算法
点格棋博弈系统的构成要素主要由搜索算法和估值函数两个部分组成[1]。传统的搜索算法是以极大极小算法为基础并加以改进而来,UCT搜索算法是近几年在计算机博弈游戏设计被逐步采用的一种算法,具有时间可控、搜索效率高的特点。
UCT算法(UpperConfidenceBoundApplytoTree),即上限置信区间算法,是将蒙特卡洛树搜索(Monte-CarloTreeSearch,MCTS)方法与UCB公式结合,在超大规模博弈树的搜索过程中相对于传统的搜索算法有着时间和空间方面的优势,UCT的工作模式是时间可控的[2-3]。在算法执行过程中的任何时间突然终止算法,UCT算法可以返回一个理想的结果。当然如果允许更为充分的执行时间的话,算法结果会非常逼近实际的最优值。UCT算法的计算方法如下:
其中,vi表示以节点ni(非叶节点)为根节点的所有仿真结果的平均值,反映了根据目前仿真结果观察到的节点ni能提供的回报值的期望;Ti表示节点ni的访问次数,也是被树内选择策略选中的次数;c表示一个参数,用来平衡深度优先还是宽度优先。
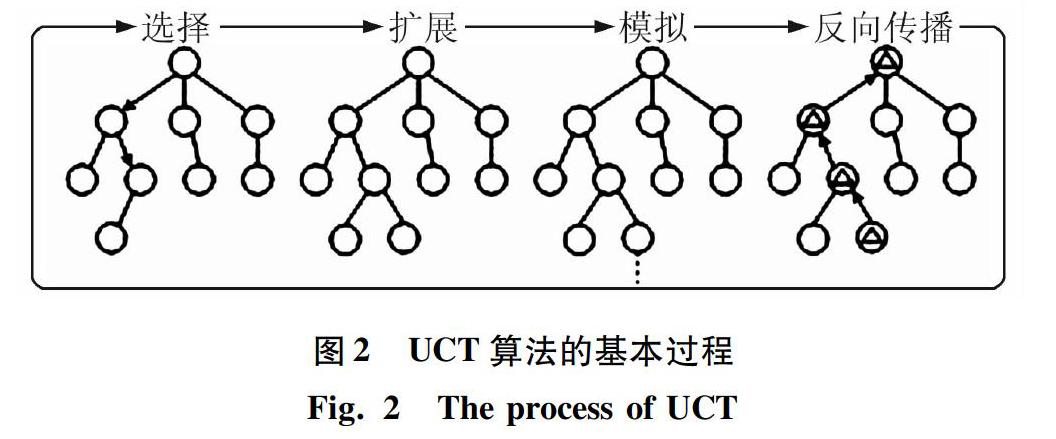
UCT算法的执行过程如图2所示。
这里,对UCT算法的4个过程的设计功能可分述为:
(1)选择:从根节点出发,用递归的方法对于每一个孩子节点进行选择,选择ri最大的节点作为下一次选择的开始,直到叶子节点。
(2)扩展:通过选择的节点,将所有合法的下法作为新的叶子节点加入到搜索树中,并正确初始化v值和T值。
(3)仿真:简单的仿真策略是对所有合法的下法,均匀地随机选择下一步,叶子节点的评估策略可以比较简单,例如:当己方获胜时为1,对方获胜时为0。通过若干次仿真后获得新的v值。
(4)反向传播:当叶子节点通过仿真获得新的v和T时,UCT算法通过结果回传更新搜索路径上的所有节点v和T的值,其计算公式为:
由式(2)、式(3)可知,父节点的访问次数T是所有叶子节点访问次数Ti之和,v是当前节点下所有叶子节点vi的加权平均值,权值为子节点的访问比例Ti/T。结果回传从叶子节点开始,沿搜索路径逐级向上更新,直到根节点。
点格棋是通过占边从而达到捕获格子的目的,而边的总数只有60条,数量相对较少,比较适合使用UTS搜索算法进行搜索。
将UCT算法结合到点格棋博弈系统中的伪码如下:
FunctionUCT(NoderootNode)
currentNode=rootNode
while(currentNode∈T)
lastNode=currentNode
currentNode=select(currentNode)//选择
lastNode=Expand(lastNode)//扩展
R=playSimulatedGame(lastNode)//模拟
while(currentNode∈T)//反向传播
currentNode=backPropagate(R)
currentNode.visitCount++
currentNode=currentNode.parent
returnbestMove
在搜索过程中,若仅采用基本的UCT搜索算法进行搜索,搜索的效率就比较低,特别是在搜索的初期,会产生大量的无效模拟,从而降低搜索效率。在采用UCT算法进行搜索过程中,引入估值,对节点的评估采用优化估值的方法进行,用以提高搜索效率和搜索的准确度。
3优化估值方法
点格棋的下法与一般棋类游戏的下法略有所不同,在完成一步下棋后,需要对是否捕获格子来做出判断,若捕获格子则要再继续下一步走棋,直到不再捕获格子为止,这个过程会导致一方连续捕获格子的情况。在博弈中后期,需要直接捕获局面,并且做出让格(中断捕获格子)、还是不让格的判断,所以在进行搜索前就要对当前局面进行评估和预处理,预处理由2部分组成,对此可阐释如下。
(1)当棋局出现死格时,直接捕获该死格。
(2)棋局中出现死树时,则对局面进行评估,根据连和环的定理判断是否留下最后两格。死格和死树的状态如图3所示。
对局面进行估值主要分为2方面。一方面是局面的控制估值,用于判断对棋局是否保持控制[4-5]。公式如下:
其中,G表示当前棋局局面[6];c(G)表示当前局面的控制值,即control_value(G);size(G)表示G中未被占领格子数;long_chain表示长链数;loops表示环的数目。tb(G)取值如下:
tb(G)=0,Ghasnochainsorloops;8,Ghasoneormoreloops;6,Ghasoneormoreloopsand3-chains;
4,otherwise.
另一方面,如果对手下边,当打开一个环,除去该环后的control_value(G)>2;或者打开一条链,除去该链后的control_value(G)>4,则己方应保持控制,否则放弃控制。
点格棋的局面估值的伪码如下:
Functionvalue()
ifcontrol_value≥2thenvalue=control_value.,
ifcontrol_value=0and
G=4l+(anythingexcept3+3),
thenvalue=0.
ifnumberof3-chains=0,orifnumberof3-chains=1
andsize(G)≡3mod4,then
ifcontrol_value+numberof4-loops≥2thenvalue=0,
1,2,3,4accordingtowhethercontrol_value≡0,±1,±2,±3,4mod8.
ifcontrol_value+4f<2then
ifGisoddthenv=1resp.3iffisoddresp.even.
ifsize(G)≡2mod4thenvalue=2.
ifsize(G)≡0mod4thenvalue=0resp.4ifnumberof
4-loopsisodd
resp.even.
inallothercases,value=1,2assize(G)isodd,even.
returnvalue
4实验与结果
在对比实验中,采用的博弈系统为相同的UCT搜索算法,节点的估值则分别采用UCB计算公式和优化估值进行计算。UCT搜索算法的時间限制分别设为:5.00s,10.00s,15.00s和20.00s。并分别设定先后手来进行对弈,得到的结果见表1。
通过表1分析发现,在采用相同的UCT搜索算法的情况下,运用估值函数的胜率要显著高于运用UCB值搜索的胜率。对于点格棋,各种局面的长链和环一般的估值并不适用。因此,该估值函数有显著优势,同时,随着每步搜索时间的增加,使用优化后的估值函数的搜索算法胜率更高。
5结束语
本文通过先后手多轮对弈比较,计算出运用UCB估值和最佳估值的不同胜率。通过胜率对比结果表可以看出,采用优化估值的方法对于局面的评估提供了一定的帮助,并能有效提高博弈胜率。
参考文献
[1]ALLCOCKD.Bestplayindotsandboxesendgames[EB/OL].[2021-02-04].https://doi.org/10.1007/s00182-020-00730-4.
[2]张宜放,孟坤.基于点格棋的UCT算法研究与分析[J].智能计算机与应用,2020,10(4):27-31.
[3]刘洋.点格棋博弈中UCT算法的研究与实现[D].合肥:安徽大学,2016.
[4]BERLEKAMPE.Forcingyouropponenttostayincontrol[J].PlosOne,2001,11(1).
[5]BREWKAG,HABELC,NEBELB.Anartificialintelligenceapproachtodots-and-boxes[C]//GermanConferenceonArtificialIntelligence:AdvancesinArtificialIntelligence.Berlin/Heidelberg:Springer-Verlag,1997.
[6]张雪峰,连莲,徐心和.基于有限自动机的“点点连格”机器博弈系统的建模与分析[J].沈阳建筑大学学报(自然科学版),2009,25(4):796-801.
