燕桥水文站水位～流量关系单值化研究与应用

一、基本情况

燕桥水文站位于江苏省徐州市铜山区三堡镇董山头村西侧灌沟河南支上，东经117°09′2.5″，北纬34°05′08″，属淮河流域奎濉河水系。2019年淮委水文局设立为省界断面水文站，系灌沟河由安徽进入江苏的省界控制站。

燕桥水文站监测断面位于燕桥上游170m 处，上游距苏皖省界700m，其间无支流汇入。河道自西向东流向，河宽33m，河道断面较规整呈U 形，河底高程27.2m，两岸地面高程31m。河段堤防较规整，左堤宽2.5m，高程33.8m，左堤外为农田；右堤宽3m，高程33.2m，右堤外为农田。

二、测流设施

土建设施：自记水位台及观测踏步、水尺桩、护岸、护坡等。

自动仪器设备：遥测水位、遥测雨量、雷达波流量计等。

人工流量监测：桥测ADCP 及流速仪法测流。

三、该站现行流量监测方法

1.桥测法

采用桥测ADCP 或桥上流速仪法测流，使用连时序法推流，工作强度大、运行成本高、时效性差、易出现人为误差。

2.雷达波流量计法

雷达波流量计属非接触式测速设备，2020年6月1日至7月22日进行人工实测流量与雷达波流量计监测的流量值同步比测。经初步分析该流量计较人工实测流量误差较大，相关关系散乱，见表1、图1。流量精度主要影响因素分析：

图1 燕桥站雷达波流量～人工流量相关图

（1）风速影响

在无降水、河道无径流情况下，由于受风速影响，雷达波流量计有较大流量数值记录，表1中第1～5 测次流量值达24.2m3/s，实际上河道流量值均为0。

（2）断面冲淤影响

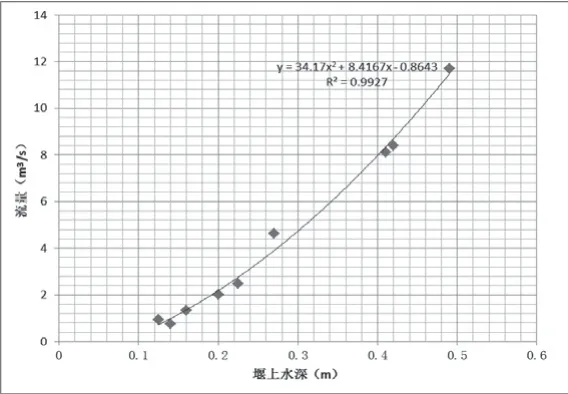
图2 燕桥站上游堰上水深～流量关系图

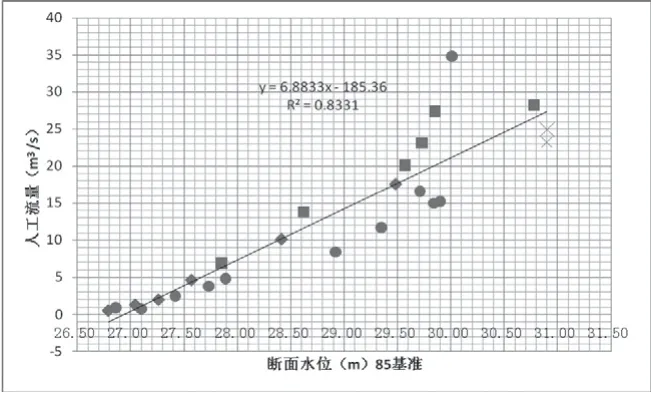
图3 断面水位～流量关系图

由于采用借用断面，当测流断面存在冲淤问题时，不能实时订正断面变化情况，导致推算流量值存在较大误差。

（3）其他因素影响

雷达波流量计识别小流速困难，表1所示第38～44 测次流量值在2～5m3/s 区间时，误差较大；特别是流量小于2.5m3/s 时，雷达波流量计流量值为0。

表1 燕桥站雷达波流量与人工流量对照表

四、流量单值化处理方法探讨

1.堰上水深～流量关系

根据该站监测河段水文特征及监测资料，测流断面以上700m 处京沪铁路桥下跌水落差2m，可消除下游支流及橡胶坝蓄水顶托等因素影响。在监测断面流量同时，同步观读堰上水深，建立堰上水深～流量关系，关系线的表达式为：

Y=34.17X2+8.4167X-0.8643，R²=0.9927，R=0.9963

根据上式可见，堰上水深～流量单一关系线趋势明显，测点离散度较小，见图2。由于该关系式系列较短，需完善大、中、小、涨落水流量实测数据，待完善资料系列、落实关系线定线与检验规范后，方可形成较为完整的流量单值化处理方法。从以上的初步分析结果看，利用堰上水深～流量关系法推算流量的方法，具备简便易行、监测强度小、精度高、成本低等优点，是较为理想的流量单值化处理方法。

2.断面水位～流量关系

相关公式Y=6.8833X-185.36，R²=0.8331，R=0.9127，相关性分析：

（1）断面水位～流量相关系数R=0.91 ＞0.80，具有较好相关性。

（2）断面水位＜28.5m 且流量＜10m3/s 时，呈单一关系。

（3）流量＞10m3/s 时关系较散乱，主要原因是受下游洪水涨落顶托、橡胶坝蓄水顶托及其他因素综合影响，导致测点的偏离较大，断面水位～流量关系呈非单一关系，见图3。

五、结论

综上所述，燕桥站流量单值化处理推荐方法有两个：

方法一：设京沪铁路桥下堰上水位监测设施，建立堰上水深～流量关系。由于燕桥站上游堰上水深～流量关系消除了下游河道洪水涨落、橡胶坝蓄水顶托等因素综合影响，具有良好的流量单一关系，因此，通过设堰上水位设施观测堰上水位，建立堰上水深～流量关系实现流量单值化。

方法二：布设燕桥下游水位监测设施，建立断面水位～流量关系。由于燕桥桥底板高出河底1m，水流存在纵向收缩，低水时易出现自由式堰流；燕桥系三孔拱桥，过水宽度14.7m，两岸河口宽度33m，具有纵向和横向收缩的量水堰特征，因此低水时该断面水位流量单一关系显著。中高水时由于受下游洪水涨落及橡胶坝蓄水顶托等因素影响，水位与流量关系离散较大，可通过布设燕桥下游水位设施，监测桥下水位，考虑桥上下游水位差影响，借以解决中高水时该站水位～流量单值化处理问题■