楔形耐张线夹-绞线有限元数值分析与优化

国网江苏省电力有限公司南通供电分公司 唐玉婷 王轶峰 李其军 南通大学 周昕恺 刘苏苏

钢芯铝绞线广泛运用于各种电压等级的架空输配电线路，耐张线夹是高压电网建设的关键金具，其对绞线的夹握力大小直接影响到输电线路的安装与铺设。楔形耐张线夹易于加工、安装方便，但仍存在握力不足的问题[1]。随着有限元法的数值分析理论和计算机技术的发展，使越来越多的复杂工程问题和结构分析用有限元法求解成为现实[2]。相比于实验法效率更高、成本更低，相比于理论分析，有限元能考虑到更多的影响因素。

为更好分析楔形耐张线夹对钢芯铝绞线的夹持性能，考虑到线夹-绞线存在的材料差异，线夹内部、绞线与线夹之间、绞线内部的复杂接触关系，以及边界加载等诸多影响绞线应力的因素[3]，建立了楔形耐张线夹-钢芯铝绞线的有限元模型。通过数值计算分析，获得到了线夹-绞线模型的应力应变分布规律，设计了正交试验，分析了楔形耐张线夹不同结构参数对线夹-绞线夹持性能的影响。

1 线夹-绞线有限元模型的建立

1.1 钢芯铝绞线模型的建立

本文以TACSR/AS-410/70钢芯铝绞线和NX-400型楔形耐张线夹为研究对象，建立其几何模型（图1）。工程运用中，各螺旋绞线层围绕中芯钢股分层顺序绞制，除中芯外相邻层绞线绞制方向相反。拉伸载荷作用下的绞线，当载荷较小时绞线处于弹性变形阶段，随着载荷的增加，铝股线的接触区域首先发生塑性挤压变形，当载荷进一步增大时绞线整体逐渐进入塑性变形阶段。为模拟绞线线材的弹塑性，建模过程中采用双线性等向强化模型，相应钢、铝材料参数为：弹性模量(GPa)180/60、切线模量(GPa)20/6、泊松比0.27/0.3、屈服强度(GPa)1.5/0.3、屈服极限(GPa)1.1/0.17、抗拉强度(GPa)1.8/0.35。

绞线模型中存在线接触与点接触，考虑到模型加载后接触位置的变形过程，且为便于接触设置，均采用面-面接触模拟绞线中的接触。由于所建实体模型为三维模型，故选用Solid185单元，目标单元TARGE170，接触单元CONTA173。

NX-400型楔形耐张线夹结构较复杂，内部包括上下楔块，外部包括2块抽匣、2块外壳、2块挂板及相应螺栓、螺母、销钉等连接件。此处对线夹结构进行了合理简化，由于线夹及绞线接触长度较长，如若完整复原其接触面会导致有限元网格划分后单元数量过多，运算时间过长，现只对部分线夹-绞线模型进行建模，减少模型尺寸长度，在保证网格划分精度的前提下降低网格数量，减少运算时间。其内楔、外楔的几何参数为：长度(mm)72/40、宽度(mm)34/50、高度(mm)12/50、楔形角度(°)2.5/2.5、线槽弧度直径(mm)28.5/6。

1.2 线夹-绞线模型的网格划分及求解参数设置

有限元模型的网格划分需兼顾计算精度和资源消耗。根据线夹相关几何尺寸及线夹内楔与绞线接触、内外楔之间接触，绞线股丝直径仅为3.5mm和4.5mm，而线夹尺寸远大于此，故在将绞线划分为细小单元时，其精度要求已大于线夹的精度要求；而在线夹与绞线的接触面上，线夹的材料硬度相比钢芯铝绞线外层铝股丝的硬度大，即内楔相较于绞线为不易变形部分。综合考虑以上两点因素，在线夹-绞线模型中划分绞线网格尺寸大小为1mm，划分线夹内外楔块网格尺寸大小为5mm。得到网格划分如图1。

图1 线夹-绞线几何模型及网格划分示意图

在线夹-绞线有限元模型中边界条件选择加载端加载方式。绞线间接触设定可将每层股丝表面节点定为一个整体，在相邻层之间建立接触对，其中少数面为目标面、多数面为接触面，摩擦系数0.3；同样设定线夹与绞线间的接触时，也将最外层铝股的表面设定为一个整体，铝股表面为接触面、内楔线槽弧面为目标面，摩擦系数0.8；内外楔线夹以小面为目标面、大面为接触面，摩擦系数0.1。设定增广拉格朗日算法，高斯接触点，设置法向接触刚度为0.01，允许侵彻系数为0.1。求解参数设定为采用3个载荷步每步迭代20次，以力为收敛准则。计算完成后，可分别查看线夹-绞线模型整体及每一零部件的等效应力、等效应变、轴向应力、剪切应力、接触应力云图及变形云图。

1.3 数值计算结果分析

根据上述线夹-绞线的有限元模型，完成线夹-绞线模型的有限元仿真分析，当绞线端面固定，线夹上施加沿绞线轴向5kN载荷时，模型整体的等效应力应变云图如图2所示。由图可知，绞线的直股钢芯和螺旋钢芯应力比外层铝股丝应力更高，但外层铝股丝对应线夹夹持位置的上下两部分股丝出现局部应力较大。这说明线夹夹持绞线时，外层股丝将受到的挤压力和摩擦力逐渐传递至内层股丝，中芯钢丝虽然承担绞线的主要张力，但由线夹直接夹持接触的部分外层铝股丝仍受到较大的挤压力和摩擦力。可看出模型整体应变分布与应力分布类似，由于外层铝股丝比内层钢股丝更软、更容易变形，绞线的股丝应力分布外层比内层大；由于线夹材料为钢材，比铝股丝更硬，故线夹整体应变比绞线大。

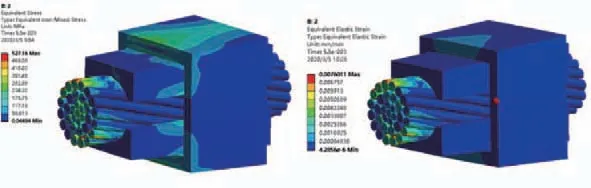
图2 线夹-绞线模型整体等效应力应变云图

绞线应力分布如图3，可看出绞线在被线夹内楔包夹的接触面上应力、应变比绞线侧面未被包夹部分应力、应变大，说明绞线在线夹夹持下，被内锲包夹的外层铝股丝将首先产生挤压变形。同时，绞线上对应线夹外楔末端位置处的应力、应变比绞线和线夹接触面其余位置的更大，说明此处为绞线受力薄弱点，这与实验所得结果相符合。

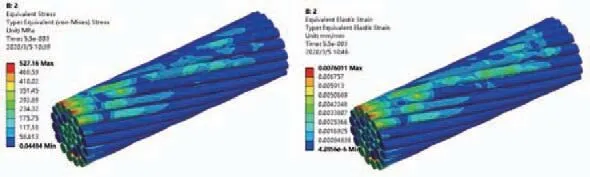
图3 绞线模型应力应变云图

线夹应力分布如图4所示，由图可看出，线夹外楔上应力、应变最大，这是由于外楔依靠其斜面结构给内楔施加压力，而外楔末端应力、应变比前端更大，是因为当绞线受到向外的拉力时外楔末端先受到挤压，且当变形量相同时末端变形比率更大，故线夹外楔末端应力、应变最大。

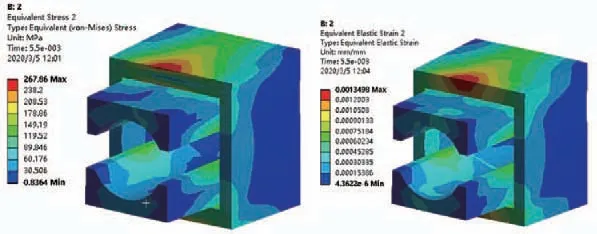
图4 线夹模型应力应变云图

2 楔形耐张线夹的结构优化设计与分析

通过对线夹-绞线有限元模型的数值仿真分析，探究线夹不同结构参数对线夹夹持性能的影响，为线夹的结构优化设计提供方向。

2.1 模型结构参数的影响

目前对线夹模型的结构参数调整从三个点来调整：线夹内、外楔的锲形角度；线夹内楔线槽的曲面半径；线夹内楔线槽的深度。对其拟定三个调整参数，分别为楔形角度(°)2.25、2.5、2.75；曲面直径(mm)28.5、28.5/30、28.5/31.5；深度(mm)7.25、7.75、8.25。为减少计算工作量，据此可将线夹结构参数可视为3因素3水平，按L9(34)正交表安排试验，通过9次试验得到与全面试验分析相同的结果，9次试验安排分别为：楔形角度(°)2.25/2.25/2.25/2.5/2.5/2.5/2.75/2.75/2.75、曲面半径(mm)14.25/15/15.75/14.25/15/15.75/14.25/15/15.75、深度(mm)7.25/7.75/8.25/7.75/8.25/7.25/8.25/7.25/7.75。

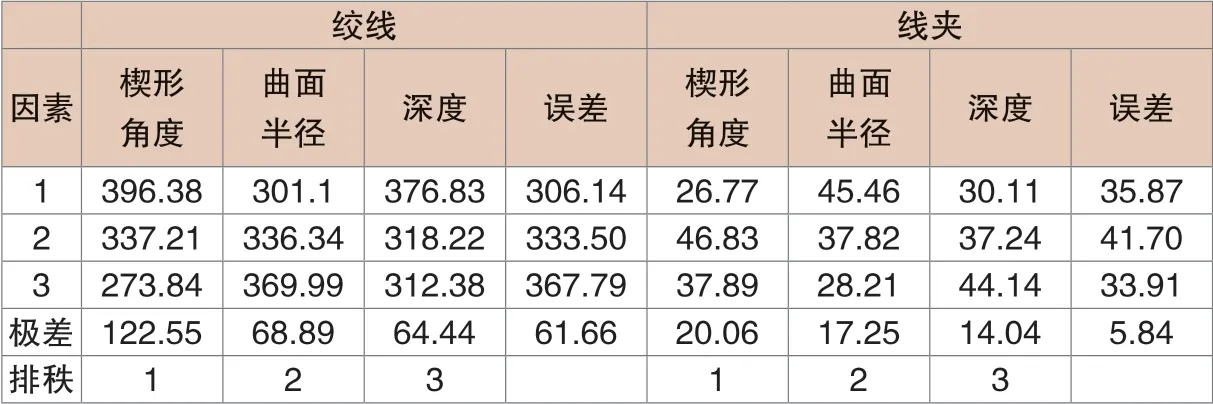
表1 绞线线夹应力极差分析

为得到线夹结构参数对线夹-绞线模型的应力影响，分别记录了9组仿真分析计算结果的绞线最大等效应力值和线夹最大等效应力值：绞线(MPa)373.02/377.01/439.12/316.89/284.64/410.09/213.39/34 7.37/260.75，线夹(MPa)26.708/32.045/21.544/51.9 51/53.179/35.36 /57.706/28.248/27.719。

对绞线最大等效应力和线夹最大等效应力分别进行极差分析，分析得出三个因素及误差对绞线应力影响比例。由表1可知，对绞线应力影响从大到小依次是楔形角度、曲面半径、深度，影响比例约为2:1:1，对线夹应力影响从大到小依次是楔形角度、曲面半径、深度，影响比例约为4:3.5:3；当楔形角度增大时绞线应力降低、线夹应力增大；曲面从圆变为椭圆，曲面半径增大、绞线应力增大、线夹应力降低；线夹内楔线槽深度增大，绞线应力降低、线夹应力增加，可发现当绞线应力降低时线夹应力增大，这说明线夹承担了一部分绞线上的应力，避免绞线因为应力过大而损坏。

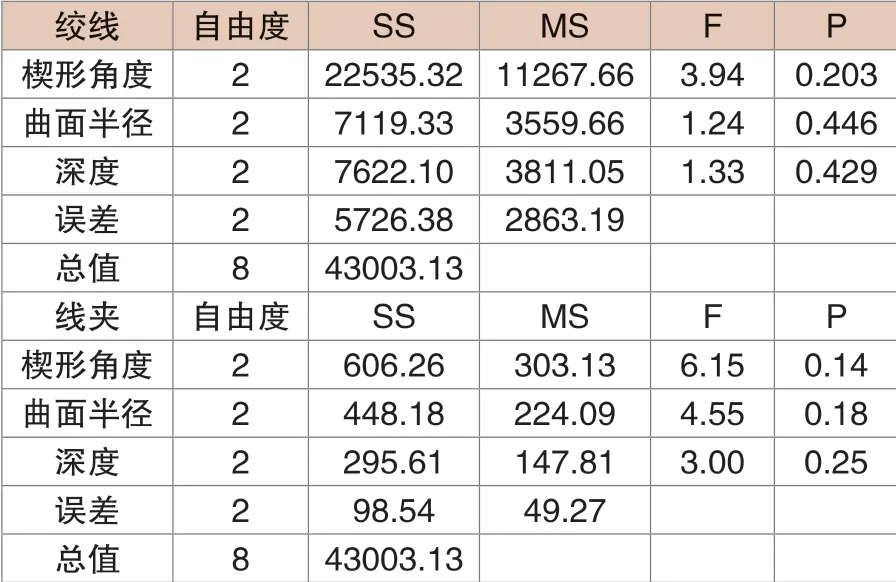
表2 绞线应力方差分析

进一步对绞线应力正交试验结果进行方差分析，由表2可知，楔形角度、曲面半径和线槽深度三个参数都存在一定显著性（F值），但其衡量显著性的指标（P值）较大，故三个因素都不是显著因素。由表1、表2可知，对楔形耐张线夹的3个结构参数进行正交试验极差分析和方差分析时发现，在正交试验结果中存在较大误差，三个因素都不是显著因素。推测在上述正交分析中，没有考虑到3个结构参数之间的交互作用，产生了模型误差，使分析结果不准确。

再次进行正交试验分析，考虑3个结构参数及参数间交互作用，依照L27二列交互作用表设计试验表头，如表3所示，其中B×C为线夹曲面半径和线槽深度的交互作用，由于交互作用自由度为4，占据两列表头。正交表进行5因素3水平正交试验，本次试验为全面试验，L27正交试验的27次绞线应力(MPa)试验结果为：208.85/235.08/242.98/254.79/241.91/227/225.63/209.87/206.75/192.89/200.97/1 86.67/210.56/211.66/200.69/252.49/235.24/231.84/218.62/191.35/153.28/204.85/175.36/191.15/217.05/213.48/203.69。

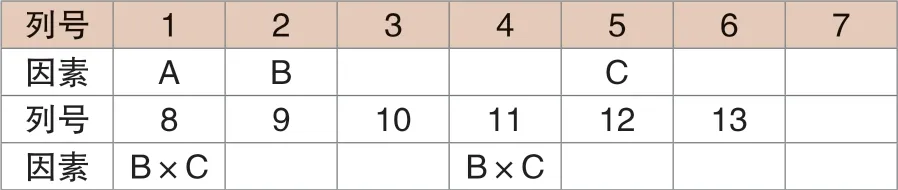
表3 L27正交试验表头

表4 绞线应力极差分析

表5 绞线应力方差分析

对L27试验结果进行极差分析和方差分析，分析结果如下表4和表5，从极差分析中可看出楔形角度、曲面半径、深度、曲面半径和深度的交互作用对绞线应力影响占比约为3.1:1.9:1.6:1，其中曲面半径增大时绞线应力增大，楔形角度和深度增大时绞线应力降低，与L9试验结果较为一致。从方差分析中可看出楔形角度是影响线夹夹持性能的显著影响。

2.2 线夹优化

根据上述正交试验结果，认为线夹楔形角度对绞线应力影响最大。楔形角度越大、曲面半径越小、线槽深度越深时绞线应力最小，选择一组最优解，楔形角度为2.75°，曲面半径14.25mm、线槽深度8.25mm时，有限元计算结果绞线应力为153.28MPa。

综上，本文以楔形耐张线夹夹持钢芯铝绞线为研究对象，建立了线夹-绞线的有限元模型并进行数值仿真分析，分析结果显示了线夹-绞线的应力应变分布规律。通过正交试验方法，分析了楔形耐张线夹锲形角度、内锲线槽深度等结构参数对绞线应力的影响，结果显示，锲形角度是影响锲形耐张线夹夹持性能的显著因素，为楔形耐张线夹的结构优化提供了依据。