基于三次元MFD和ARIMA模型的区域宏观交通状态预测方法

王 鹏 飞

(1 河北科技师范学院城市建设学院，河北 秦皇岛，066004；2 北京工业大学城市与工程安全减灾教育部重点实验室)

为了能够准确获知路网车流的实时运行状态，进而对交通流进行诱导与控制以缓解交通拥堵，工程师在道路网中布设了各式各样的检测器(线圈检测器，浮动车)。但是，管理者通过各路段上零散的交通信息想对路网整体的车辆运行状态进行预测和控制依旧十分困难，这是由于非线性的交通流现象与用户不可预测的路径选择行为相互作用的结果。为此，Daganzo[1]提出了可以表征路网总流量与路网车辆数关系的宏观交通基本图(Macroscopic Fundamental Diagram，MFD)，随后，Geroliminis and Daganzo[2]通过对日本横滨商业中心的检测器数据进行分析，验证了MFD在现实城市路网中的存在性。近年来，国内外学者以不同的城市高速公路网，或以不同的城市道路网为研究对象，对MFD的特性进行了诸多实证研究并取得了很多成果[3～6，7～11]。但这些研究所需要使用的数据均为数天的检测器数据，因此很难验证MFD是否具有良好的再现性。对此，在国外，Wang等[12，13]以日本仙台市、京都市作为研究对象，利用1年的检测器数据对MFD进行分析，发现在外部条件(工作日/节假日，天气状况等)相似的情况下，MFD的形状变化不大。换而言之，得出了MFD拥有良好再现性的结论。在国内，张南等[14]利用近2个月的检测器数据对路网中不同道路的基本图进行描绘，发现不同道路上的基本图的形状特征也相对稳定。

上述实证研究已经发现，MFD在一定条件下具有良好的再现性，而这是将MFD概念应用到实践的重要依据。在应用研究领域，目前以基于MFD的区域边界交通流控制策略研究为主，对此诸多学者已经取得了丰硕的成果[15]。笔者以MFD在一定条件下具有的良好再现性为基础，结合常用于时间序列分析的ARIMA模型构建可预测未来短时的路网宏观交通状态(路网总流量，路网车辆数)的模型。在以往的研究中，使用ARIMA模型或与其他模型相结合来预测某一条道路未来短时交通流量的研究并不少见[16～21]，但将ARIMA模型与区域交通历史数据相融合，结合三次元MFD来预测宏观区域交通状态的研究在国内外尚无先例。

1 宏观基本图描述方法

Daganzo[1]将MFD定义为路网总流量(Traffic Production，单位：辆·km/单位时间，即单位时间内通过路段的交通量与其所在路段长度的乘积求和)与路网车辆数(Traffic Accumulation，单位：辆，即单位时间内对各路段上存在车辆数求和)之间的关系(式(1)，(2))。

P(t)=∑iqi(t)li

(1)

N(t)=∑iki(t)li

(2)

其中，li为第i条车道(路段)的长度；qi(t)为第i个检测器在时间段t内检测到的交通流量(笔者采用t=5 min)；ki(t)为第i个检测器在时间段t内检测到的交通密度。P(t)为时间段t内的净车公里数，N(t)为时间段t内的路网车辆数。

2 预测模型构建

2.1 基本模型

在本次研究中，反映路网宏观交通状态的路网总流量与路网车辆数的预测值是由趋势项与随机项两个部分组成的(式(3)，(4))。其中，趋势项反应同一条件下的历史数据的实时变化趋势；而随机项则代表预测当天MFD形状特征的微小变动，笔者利用ARIMA模型进行计算。

(3)

(4)

2.2 趋势项

趋势项的定义为同一条件下和同一时刻的历史数据(路网总流量、路网车辆数)的算数平均值(式(5)，(6))。

(5)

(6)

其中，D为同一条件下的同一时刻的历史数据个数(即以天为单位的日数)，即文献[12，13]中所述的由层次聚类分析方法所得到的每一簇的元素个数。

2.3 随机项

随机项用于描述预测当天MFD相较于历史数据的波动情况，由ARIMA(m,d,q)模型计算得出。其中，m为AR模型的最高阶数，d为时间序列变为平稳时所做的差分次数，q为MA模型的最高阶数(详见文献[22])。式(7)与式(8)分别表示预测当天的路网总流量与路网车辆数相对于历史趋势项(式(5)，(6))的波动量。

(7)

(8)

2.4 模型评价

对于模型的预测精确程度，笔者采用相对误差(式(9)，(10))以及平均绝对误差(式(11)，(12))来进行评价。

(9)

(10)

(11)

(12)

其中，T为时间段数量。

3 实例分析

3.1 研究区域

那霸市是日本冲绳县首府，也是冲绳县最大的城市，人口约82万。路网中，单方向路段由1～3条车道组成，交叉口间距100～300 m，信号周期白天约为90 s，夜间约为120 s。笔者以日本冲绳县那霸市的商业中心路网(图1中虚线以内路网)为研究对象，在图1所示区域内共有133个地点布设有检测器，它们收集着每5 min的交通流量及车速。本次研究以2012年5月1日～ 31日的检测器数据为研究对象，对其中全天24 h均为晴的普通工作日的每30 min的区域宏观交通状态进行分析。

图1 日本冲绳县那霸市商业中心路网(来源：百度地图)

3.2 预测结果及分析

笔者使用层次聚类分析方法对2012年5月1日～5月31日历史数据进行分类，且从中找出全天24 h均为晴的簇(聚类分析结果的树状图见图2)。然后利用该簇中D-1 d的检测器数据对另外1 d的宏观交通状态进行预测，下文中首先对聚类分析结果进行详细说明。

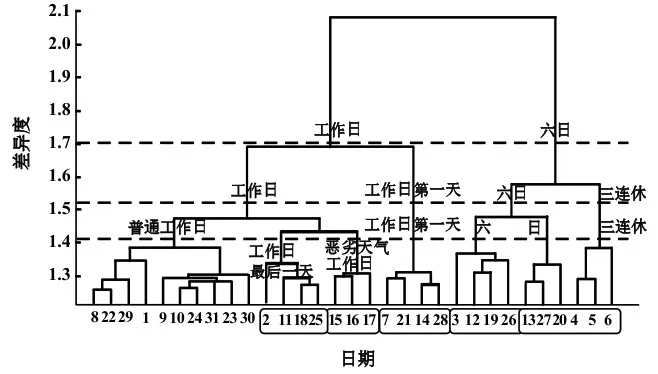
图2 基于层次聚类分析方法的3次元MFD的分类结果(2012-05)

3.2.1聚类分析结果由分类结果中可知，无恶劣天气的普通工作日{1,8,9,10,22,23,24,29,30,31}(无框)，工作日第1天{7,14,21,28}，工作日最后1天{2,11,18,25}，周六{3,12,19,26}，周日与法定假日{4,5,6,13,20,27}，较恶劣天气的普通工作日{15,16,17}是可以很清楚被区分的。由此可知，在宏观层面上，若外在条件较为相似，则MFD拥有良好的再现性。从微观上分析，这种结果是由大量用户的规律出行所导致的。例如：工作日第1天一般拥有明显早高峰和不突出晚高峰的特点；而工作日最后1天则往往相反。

由此可见，若单纯利用三次元MFD的再现性是可以对预测当天的区域宏观交通状态进行粗略估计的，但此方法对于MFD中常见的磁滞现象[23]或因突发事件所导致的路网总流量下降、进而产生大规模交通拥堵等现象却不能准确预测。因此，还必须结合常用于时间序列分析的ARIMA模型才能够实现更加精准预测。

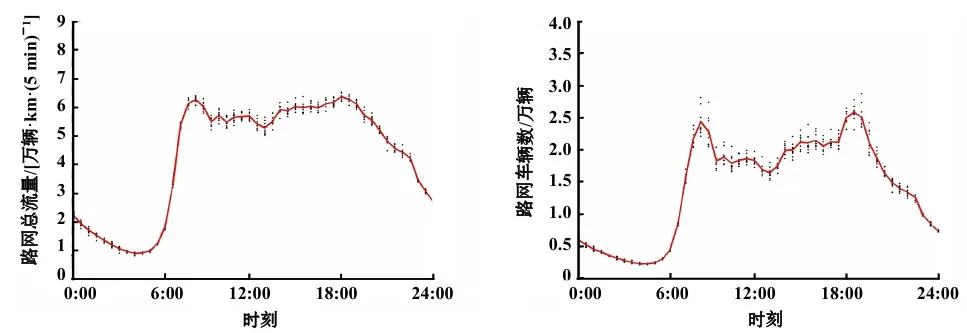
图3 趋势项的计算(2012-05)

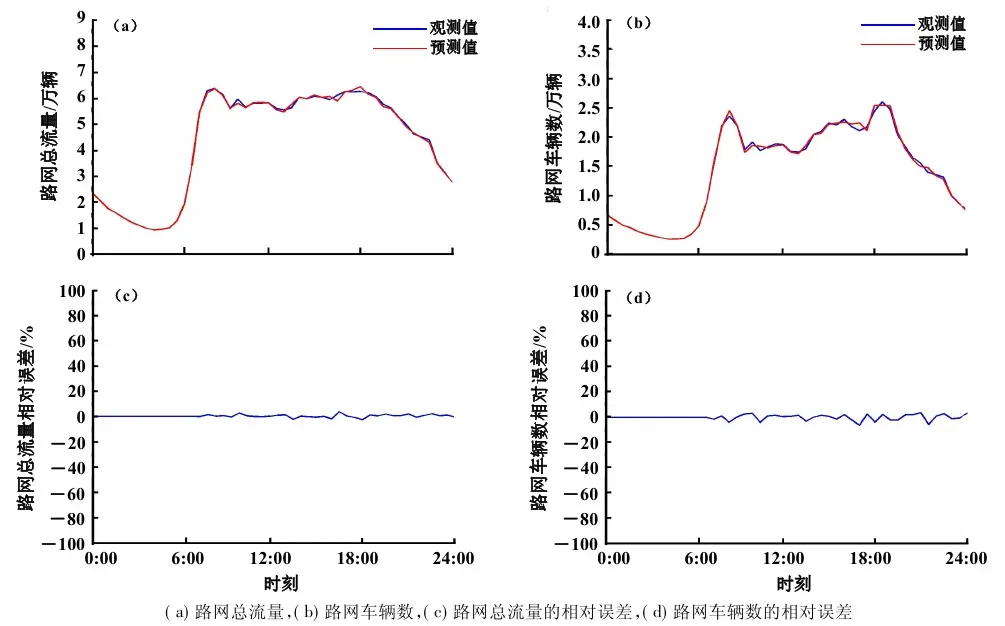
(a)路网总流量,(b)路网车辆数,(c)路网总流量的相对误差,(d)路网车辆数的相对误差图4 每30 min的预测结果及精度评价实例(05-10)

3.2.2区域宏观交通状态预测结果本研究首先以图2所示的一天24 h全部为晴的普通工作日，即集合{1,8,9,10,22,23,24,29,30,31}中的路网总流量，路网车辆数作为历史数据计算趋势项。其中，图3中所示的红线即为利用式(5)，(6)计算得到的趋势项。其次，以上述普通工作日的0:00～8:00的数据作为标记ARIMA模型参数的初始数据，而后通过式(7),(8)计算随机项。其中，5月10日的实时预测结果与相对误差如图4所示，5月所有日期的预测结果精准程度评价见表1。由此可知，利用三次元MFD与ARIMA模型相结合的方法可以以较小的误差，预测未来30 min的宏观交通状态。

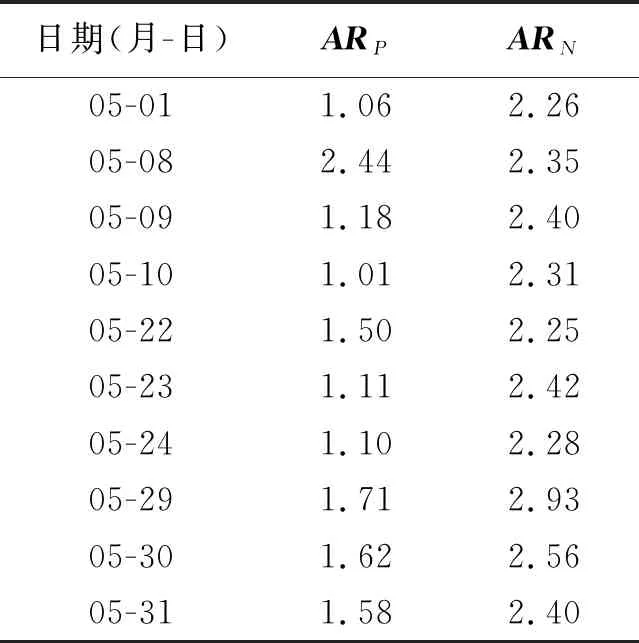
表1 绝对平均误差(2012-05) %

4 结论与讨论

本次研究通过对外界相似条件下的路网总流量、路网车辆数的历史数据与预测当日早高峰前的数据进行融合，提出了基于三次元MFD和ARIMA模型的路网宏观交通状态短期预测方法。而后，通过实例分析得出了此方法可以以很小的相对误差预测未来30 min的路网宏观交通状态的结论。在实践方面，道路管理者可考虑利用此方法向用户提供某个特定区域未来30 min的宏观交通运行情况，以便让用户在出行前就可以对出行目的地、出行方式等进行准确的选择。

此外，本次研究还存在若干可以拓展的方向：(1)若考虑更多影响MFD形状特征的因素，可将历史数据进行进一步的分类整理，进而计算得出更为精准的趋势项。(2)若将公共/共享停车泊位的预约制度或停车许可证制度[24～27]纳入到基于MFD的建模理论中，则道路管理者可以在用户出行前就掌握原本无法观测到的路网内部流入流出交通量，此组合策略将有望进一步提高对路网宏观交通运行状况的预测精度。(3)若将MFD与网络交通流分配理论相结合，则可能会进一步提高每条路段上交通流状态预测的精度[28]。