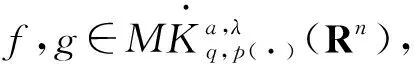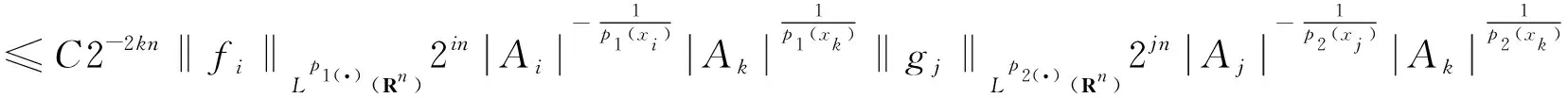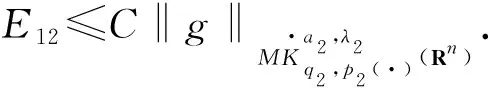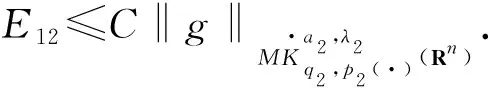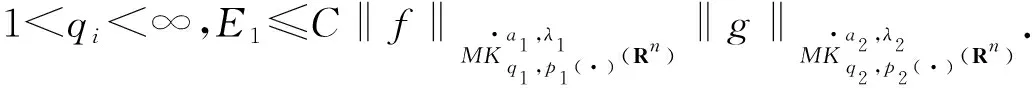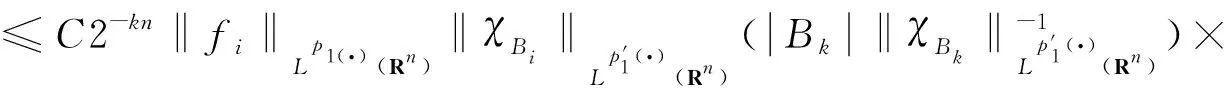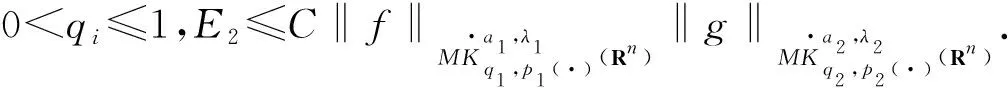多线性Marcinkiewicz算子在变指数Herz-Morrey空间上的有界性
2021-05-10叶晓峰
叶晓峰,韩 晶
(华东交通大学 理学院,江西 南昌 330013)
多线性算子的研究吸引着很多研究者,许多结果与经典算子的线性理论相似,但也发现了一些新现象[1].二十世纪九十年代一些学者开始研究变指数函数空间上的一些性质[2],近年来,变指数函数空间在调和分析中得到长足地发展[3-5].Izuki[6]引入了变指数Herz-Morrey空间,Lu等[7]研究了次线性算子在此空间上的有界性.Zhu等[8]研究了带可变核Marcinkiewicz积分算子变指数Herz空间上的有界性.受此启发,本文主要讨论的是多线性Marcinkiewicz算子在变指数Herz-Morrey空间上的有界性.
设B(x,r)={y∈Rn:|x-y|
1 定义
则根据上述多线性算子F定义多线性Marcinkiewicz算子μ为
μ(f1,…,fm)(x)=
定义2[2]设p(·):E→[1,∞)是一个可测函数.
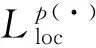
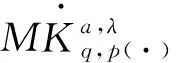
其中范数表示为
定义3[9]核函数K满足的尺寸条件定义如下:对所有的x,y1,…,ym∈Rn,且存在1≤j≤m,满足x≠yj,有
2 引理
引理1[10]当0 引理2[11]如果p(·)∈P(Rn)存在一个常数C>0,且对于所有球B在Rn中,下面不等式成立 引理3[10]如果p(·)∈P(Rn),存在常数0<γ<1和C>0,对任意的球B⊂Rn和对任意的可测子集S⊂B,有下面的不等式成立 这里隐含常数不依赖r且x∈R. 其中 设E是Rn中的开集,如果p(·)∈P(Rn)且满足下面2个条件: 则有p(·)∈B(Rn). 根据变指数Herz-Morrey空间的定义 从以上的四个等式中可看出E2和E3对称,则只要分析E1,E2,E4即可.根据核函数K满足尺寸条件和Minkowskiw不等式,可得到 肿瘤转移是癌症相关死亡的主要原因。转移前微环境的形成是肿瘤转移的关键步骤[1]。肿瘤转移研究领域先驱David Lyden教授发现原发肿瘤分泌的细胞因子为肿瘤细胞在转移灶的定植提供了有利的条件,并提出了转移前微环境的概念,彻底改变了人们对转移级联反应的认识[2]。目前已经可以确定的是,肿瘤细胞的远端转移器官不是循环肿瘤细胞(circulating tumor cells,CTCs)的被动接受者,而是转移扩散发生之前原发性肿瘤主动选择性修饰的“土壤”,以利于播种转移的“种子”[3]。 由中值定理可以得到 由E1得到i≤k-2,j≤k-2,|x-y1|~|x|~2k,|x-y2|~|x|~2k,其中x∈Ak,y1∈Ai,y2∈Aj. 则根据引理5和中值定理所得的上面式子可得 则根据上述分析可得到 由引理4可得 当0 由E2得j≥k-1,i≤k-2,且|x-y1|~|x|~2k,|x-y2|~|max{|x|,|y2|}|~max{2j,2k}.其中x∈Ak,y1∈Ai,y2∈Aj.当j≥k-1,有2种情况.当k>j时,B1,B2和E1中的B1,B2得到的结果一样,当k 注意到‖χi‖Lp(·)(Rn)≤‖χBi‖Lp(·)(Rn). 经上述分析可得到 ‖μ(fi,gj)(x)‖Lp(·)(Rn)≤C2-kn‖fi‖Lp′1(·)(Rn)‖χBi‖Lp′1(·)(Rn)‖χBk‖Lp1(·)(Rn)× 2-jn‖gi‖Lp2(·)(Rn)‖χBk‖Lp2′(·)(Rn)‖χBk‖Lp2(·)(Rn) 由引理2可得 由引理3可得 当0 当1 E223和E221的形式一样,E224和E222的形式一样,则用同样的方法估计不等式可得到 由E4可注意到i>k-1,j>k-1.分下面4种情况:当i 同E2中‖μ(fi,gj)(x)χk‖Lp(·)(Rn)的方法一样,用引理2和引理3可得 E41和E42的形式和E22的形式一样,则可得到 综上分析,证明了此定理.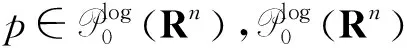
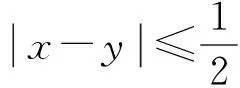
3 主要结果