基于深度神经网络的智能推送系统研究*
2021-05-10毕波,许静
毕 波, 许 静
(马鞍山师范高等专科学校1.软件工程系;2教师教育系,安徽 马鞍山 243041)
0 引 言
推送系统有利于提高用户对服务的参与度和总体满意度,在协助用户选择方面越来越受欢迎[1]。推送系统是信息和电子商务系统的重要组成部分,个性化推送系统的智能推送功能可以有效地从海量互联网数据中为用户提供有价值的信息。推送系统已被研究并应用于不同领域的在线服务中,例如音乐[2]、视频、社交、工作、职位[3]等。随着人工智能技术的发展,越来越多的智能产品被应用在日常生活中,并在各个方面为人们提供了便利。深度神经网络(DNN)在各个领域都取得了巨大的成功,一些研究人员最近提出了基于深度学习的推送模型,但是其中大多数模型都使用与应用有关的附加特征(例如文本内容和音频信息)来增强其性能。考虑到大多数推送系统可能很难获得上述信息,提出了一种基于深度神经网络的推送模型,该模型不需要用户和项目之间的交互,也不需要任何额外的信息。
1 特征表示模型
在本方法中,需要根据评分矩阵获得用户和商品的特征。在本节中,将讨论各种特征表示方法。
令n个用户对m个项目的用户项目评分矩阵为R。矩阵的元素Rij代表第j个项目的第i个用户的评分。如果不存在评分记录,则Rij等于0。此外,令用户的潜在特征矩阵为U,第i行的向量Ui代表第i个用户的特征。而项目的潜在特征由矩阵V表示。
(1)评级特征。评级特征是一种特征表示方法,其主要思想是将用户的评级数据直接视为用户的特征,即U=R,同样,项目的特征是V=RT。
尽管评级特征的方法简单有效,但也存在一些不足。评分矩阵非常稀疏,因此有许多丢失的数据。如果没有仔细处理丢失的数据,则结果模型可能不够准确,并且找到合理的方法来处理此类数据可能需要进行大量额外工作。
(2)ID特征。用户或项目的ID是唯一的,因此可以将其视为所需的特征。但是,ID是无法比较或无法进行其他数学运算的分类变量。因此,He等人[4]提出了一种称为神经协同过滤(NCF)的方法,如下所示:,
Ui=NN(OneHot(i))
(1)
Vj=NN(OneHot(j))
(2)
其中,OneHot(i)表示使用One-Hot方法对IDi进行编码,这将生成具有指定维数的零向量,并且该向量的第i个位置将设置为1。NN(x)表示当输入为x时神经网络的输出。
(3)奇异值分解。矩阵分解技术在减小尺寸和特征表示的情况下实现了强大的性能。因此,当需要从矩阵学习特征时,这是一个可行的选择。奇异值分解(SVD)算法是最著名的矩阵分解算法之一。 该算法将矩阵分解为三个矩阵,从而获得用户和商品的特征。SVD的表达式如下:
R=USVT
(3)
其中对角矩阵S的对角元素由矩阵R的特征值组成。此方法还需要预处理大量缺失值,由于在求解特征值时复杂度很高,因此在处理大规模数据时性能较差。
(4)概率矩阵分解。概率矩阵分解(PMF)算法[5]使用用户的潜在特征和项目特征的乘积来获得相应的评分。当最小二乘误差用作损失函数时,表达式如下:
(4)
其中参数λ1和λ2表示λ2常规参数。 由于存在缺失值,在计算损失时不应考虑这些缺失值,因此修改后的损失函数如下:
(5)
其中,当Rij为零时δij=0;否则δij=1。可以看出,PMF算法可以有效避免值丢失的问题。但是,该算法的基本假设是用户和商品的功能完全独立,而且不同功能之间可能存在一定的相关性。
(5)二次多项式回归。考虑到上述方法的缺点,提出了一种基于二次多项式回归(QPR)的特征表示方法,不仅避免了缺失值的预处理可能导致不准确的问题,还可以考虑特征之间的相关性。
在传统的二次多项式回归模型中,对于特征向量x,对应的监督值y由以下表达式表示:
(6)
其中参数l表示向量x的维数,z表示常数项的系数,w表示一阶系数,W表示二阶系数。因此,在提出的方法中,x=(Uu,Vv),和y=Ruv,于是有
(7)
令
(8)
(9)
然后可以看到,pu仅与用户u有关,而qv仅与项目v有关。因此,获得了最终模型:
(10)
与PMF算法一样,QPR的训练损失通过最小二乘法进行评估。 因此,有
(11)
通过优化方程 (11)来最小化L,可以获得需要的两个矩阵U和V。
2 深度神经网络模型与训练
2.1 深度神经网络模型
在本小节中,将介绍使用的深度神经网络模型,该模型将用户和项目的潜在特征作为输入,并使用前向传播算法来预测评分。根据本模型,在输入层中,输入向量x0由用户和项目的潜在特征连接在一起。因此,对于任意记录Rij,都有
x0=concatenate(Ui,Vj)
(12)
其中函数concatenate()用于连接两个向量。当x0穿过第一个隐藏层时,第一个隐藏层的输出可通过以下公式获得:
x1=activation(W1x0+b1)
(13)
其中W1是输入层和第一个隐藏层之间的权重矩阵,b1是偏置矢量,activation()表示激活函数,该函数旨在使神经网络模型非线性。在DNN模型中,常用的激活函数包括sigmoid、tanh和ReLU函数。在文中,选择ReLU作为模型的激活函数,因为它更有效并且更易于优化。
由式 (13),可以获得第l个隐藏层的输出:
xl=ReLU(Wlxl-1+bl)
(14)
在输出层,训练的目标是预测用户的评分得分Rij。再次使用One-Hot编码方法来获得监督值y。因此,需要通过softmax方法对输出结果进行变换,以获得y对应位置的预测值,即
(15)
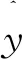
(16)
其中d表示向量y的维数,它等于输出层中神经元的数量。最后,本模型通过以下等式预测第j个项目的第i个用户的评分得分:
(17)
2.2 训练模型
在本小节中,将描述模型的训练细节。 首先,需要使用QPR模型来获取特征。使用梯度下降法求解问题(11),学习率设置为η,更新每个参数的规则如下:
(18)
(19)
(20)
(21)
(22)
(23)
其中,
(24)
讨论深度神经网络模型的训练方法。深度神经网络的训练主要基于权重矩阵W和偏置向量b的学习。定义Wl,ij为代表第l层的第i个神经元和第l-1层的第j个神经元之间的连接权重。第0层代表输入层,bl,i代表在第l层中的第i个神经元上的偏置。
使用梯度下降法对W进行求解,于是有
(25)
Wl,ij仅会通过神经元i影响损失ε,因此使用netl,i表示第l层中神经元i的加权输入:
(26)
于是有,
(27)
当l层是输出层时,
(28)
当l层是隐藏层时,
(29)
基于以上讨论,获得了以下规则来更新DNN模型中的参数:
(30)
(31)
3 实验评估
在实验评估中,使用真实的数据集来测试模型的性能。该数据集包含关于168个项目的943位用户的近100,000条评分记录,该数据集来自MovieLens网站。实验所采用的服务器配置有一个英伟达TITAN GPU,CPU是英特尔酷睿i7,内存为64GB,操作系统是Linux Ubuntu 16.04,深度学习框架为Tensorflow。采用均值绝对误差(MAE)方法和均方根均方根误差(RMSE)来评估模型的性能。
在深度神经网络模型中,隐藏层数设置为2。在输入层中,神经元数是34,第一个隐藏层中的神经元数是27,第二个隐藏层有12个神经元,输出层有5个神经元,学习率设置为0.001。随机选择数据集的20%数据作为测试集,其余80%作为训练集。
将验证本方法的预测精度,精度的MAE和RMSE如图1所示。其中,SVD为基于奇异值分解的方法,DsRec[6]是结合了矩阵分解和聚类的方法,PMMMF[7]是基于近似支持向量机的方法。本方法的MAE和RMSE指标下均实现了更好的性能,这意味着我们的模型获得了更高的预测准确性。从实验结果可以看出,在相同条件下,RMSE值大于MAE值,这意味着RMSE度量标准可以更好地反映算法性能。
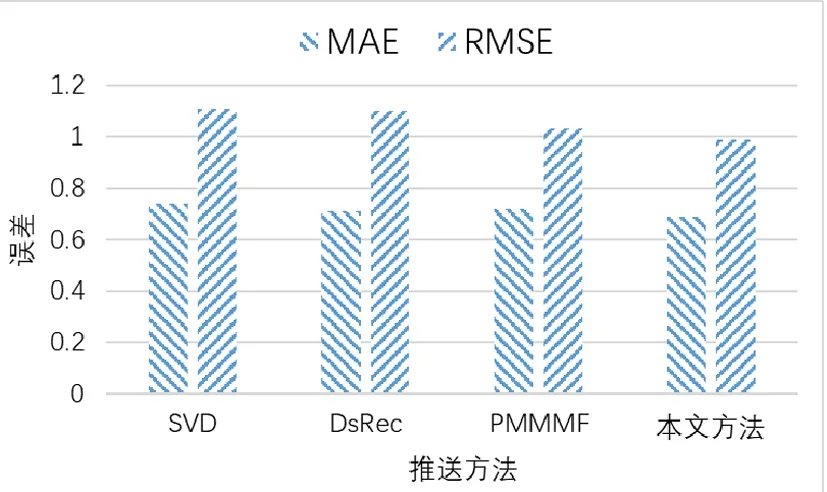
图1 推送方法误差对比
4 结 语
探讨深度神经网络模型在智能推送系统中的应用,提出基于QPR模型的特征获取方法,并将其与DNN模型结合起来。实验结果表明,提出的模型具有良好的预测性能。未来的工作将集中在构建更复杂的模型和使用其他深度学习方法。将研究其他深度学习技术的应用,例如卷积神经网络方法在推送系统中的应用,并尝试进一步提高其性能。
