卧式退火炉炉辊带钢张力研究

张 冉

(宝山钢铁股份有限公司硅钢部,上海 200941)

水平卧式退火炉,炉辊均以托辊形式控制炉内张力。为了提高退火炉张力控制的稳定性和精度,应从炉内传动的执行机构入手,分析各设备的工作原理和相关理论模型。通过理论解析和建模,分析影响张力控制的关键环节,并根据实际工业需求进行参数优化,以满足各种规格产品的生产能力,提高产品的性能参数,符合企业的精品战略。

1 异步电动机矢量控制模型

1.1 电动机等效电路分析

在异步电动机的研究领域,通常使用等效电路的方式对电动机参数进行辨识。通过矢量控制的原理,得到电动机工作状态下的各项旋转参数。工业自动化控制领域中,任何张力调节系统的最终目的,都是通过电动机的速度控制转化为电动机转矩的变化,以此形式调整张力的变化量。转速又通过控制电动机旋转的电流进行调节,因此需对电动机进行转速、转矩间的关联分析,研究两者与电流之间相互作用的控制模型[1]。电动机转动惯量方程如式(1):

(1)

式中:Telec为电动机电磁转矩;Tload为电动机负载转矩;J为电动机转动惯量;ω为电动机旋转角速度。

由式(1)可知,交流电动机由电动机旋转速度的变化产生电磁转矩[2]。矢量控制理论建立的原理依据,即将异步交流电动机的旋转状态进行运动坐标的变换,使异步交流电动机等效为直流电动机。励磁后调节输出电流的大小改变电动机转速,进而控制电磁转矩的输出[3]。

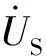
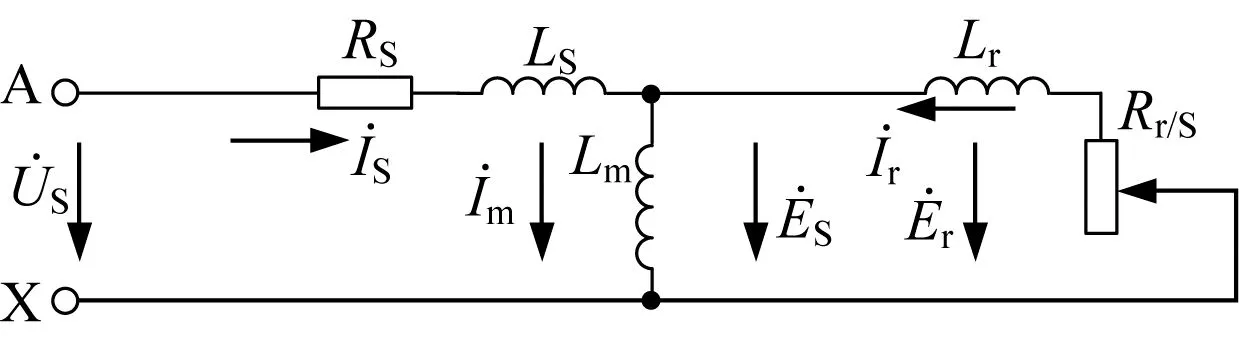
图1 异步电动机稳态等效电路图

稳态转矩Te为:

(2)

因ES可表示为ES=ωS·ψS,则转矩公式Te又可写作:

Te=pψSIS

(3)

式中:ψS为定子磁链;p为电动机极对数;ωS为输入电压角频率。

稳态下假定定子磁链ψS恒定,则转矩大小仅与定子电流IS的大小相关,IS可表示为:

(4)

式中:s为电动机转差率。

式(4)代入式(3)可得:

(5)

式(5)表明当三相异步电动机定子磁链ψS恒定时,输出转矩Te等效为直流电动机输出转矩,那么为使电动机磁链ψS恒定,需对电动机磁链进行如下计算。

转子磁链方程:

(6)

定子磁链方程:

(7)

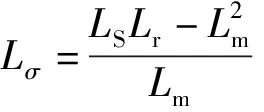
由等效电路可推导出异步电动机定子磁链方程:

ψS=LmISM

(8)

若定子电流的相位分量ISM恒定不变,磁链与电动机转矩可控[6]。因定子及转子磁链方程的耦合关系,控制炉辊电动机输出转矩需通过矢量空间方程继续研究定子电流与转子电流间相互作用的关系。

1.2 电动机定子和转子矢量方程

图2为三相异步电动机静止状态下的绕阻模型,A、B、C分别为定子绕阻坐标轴线,a、b、c为转子绕阻坐标轴线,电动机转子的旋转角速度ω,以矩阵形式对静止坐标系下的电动机状态方程进行表述。

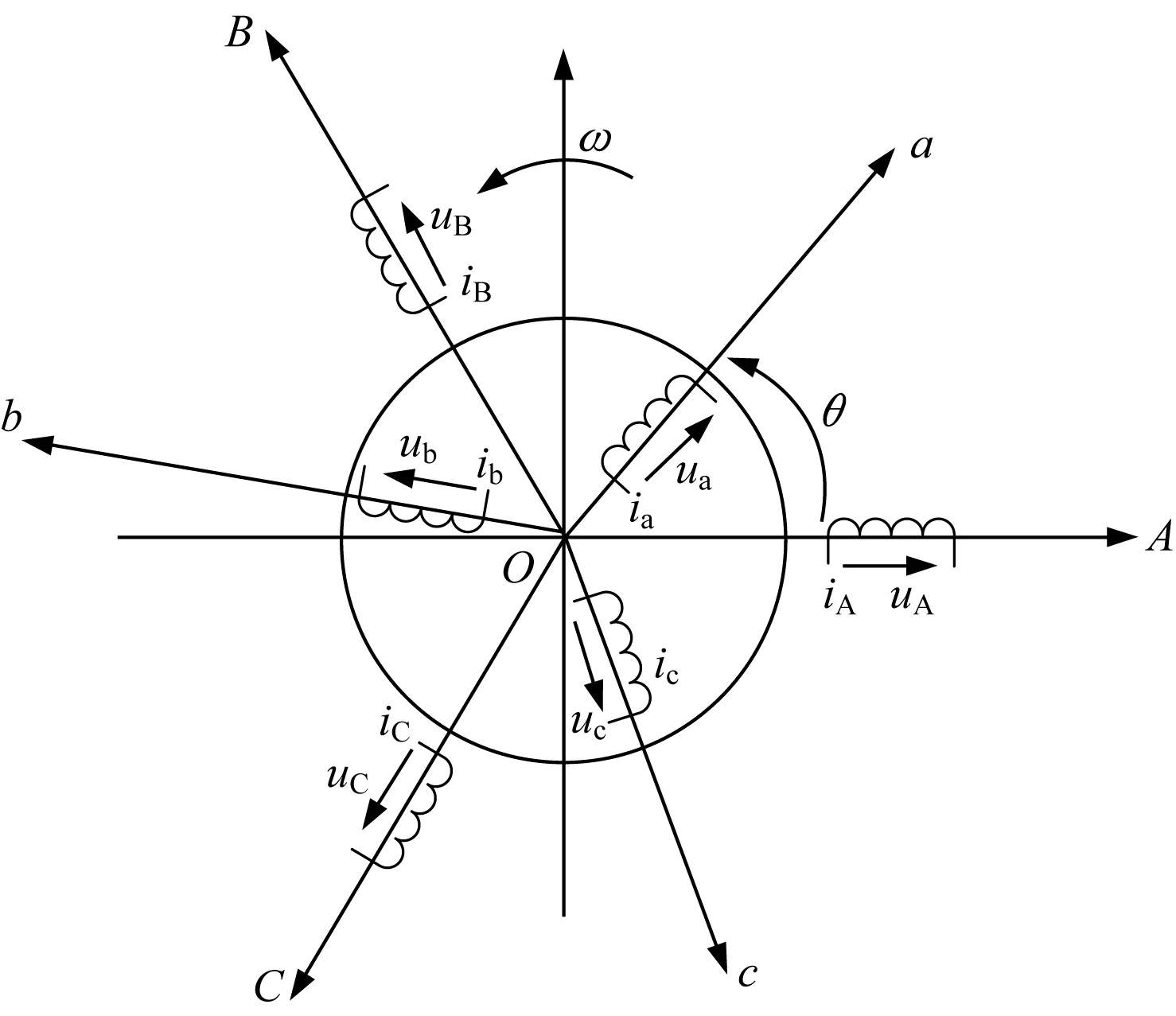
图2 异步电动机绕阻模型

电压方程:

u=R·i+ψ

(9)

电压向量:

(10)

电流向量:

(11)

磁链向量:

(12)

电阻矩阵:

(13)

式中:u为定子、转子瞬时电压值;i为定子、转子瞬时电流值;ψ为定子、转子磁链;R为电阻。

磁链方程为:

ψ=L·i

(14)

令ψ=[ψS,ψr]T,i=[iS,ir]T,磁链方程转为矩阵形式:

(15)

(16)

式中:LiS,Lir为定子、转子漏感;LmS,Lmr为定子、转子互感,假设定子、转子匝数、绕阻的互感磁阻相等,则Lmr=LmS;θ为定子、转子绕阻的空间角位移变量,对LSr和LrS矩阵进行互为转置。

根据能量守恒和电能转换原理,电磁转矩Te可表示为电磁转矩方程:

(17)

代入运动方程:

(18)

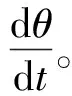
经电动机学中的空间坐标转换公式,最后分别得出不同空间坐标内转矩公式。

αβ空间:

(19)

dq空间:

(20)

mt空间:

(21)

mt坐标系中的转矩方程,定子电流分量为iSm、iSt,iSm与磁链ψr之间存在一阶惯性环节传递函数,与直流电动机励磁绕阻的励磁惯性环节类似。ψr的变化取决于定子电流分量iSm,同时iSm的变化量与Te成正比。在mt坐标系中解耦iSm及iSt分量,即可通过电流与电动机输出转矩间的函数计算值,控制电动机的转矩输出[7]。结合转矩矢量控制算法[8],调节炉辊电动机的输出转矩,对炉辊传动进行退火炉的张力控制。

αβ、dq空间坐标中的电动机力矩系统方程存在耦合关系,难以通过常规计算得出转矩与电流的关系。但两空间坐标系统均显示负载转矩TL对电动机输出转矩的影响,其变化量与控制性能的下降有直接关系[9]。优化负载转矩计算值的精确性,可有效减小退火炉张力的计算误差。

2 逆变单元的电压控制模型

炉辊的逆变单元采用矢量控制的方式,将整流器输出的直流母线电压转换为可变频率的交流电压。基于脉宽调制技术PWM,控制逆变电路内功率元件IGBT,输出等幅值电压脉冲控制电动机输出的转速、转矩[10]。其形式为使输出周期内含多个电压脉冲,构成正弦波目标波形。使正弦波中脉冲的等值电压均稳定且不含低次谐波,控制脉冲的宽度及频率,实现调整逆变电路的输出电压值及输出频率[11]。然而交流电动机调速的目的是得到相应的电磁转矩,该电磁转矩必须依靠旋转磁场才能得到。因此将电动机与逆变器合并为同一系统,通过旋转磁场中系统的状态动态调节逆变器的工作参数,输出控制电动机运转的等效电压。最终通过系统回路中的电感、阻抗等数据的计算,调节电动机的工作电流值及励磁磁链值[12],进而控制电动机转速与输出电磁力矩。

通过图3转子磁链的电压模型可观测到,电动机αβ空间坐标系中磁链ψ与电流分量i存在耦合关系,但电流分量可由磁链方程经电动势积分后带入消除,最终将逆变器电压与磁链关联,作为逆变单元的可控模型[13]。

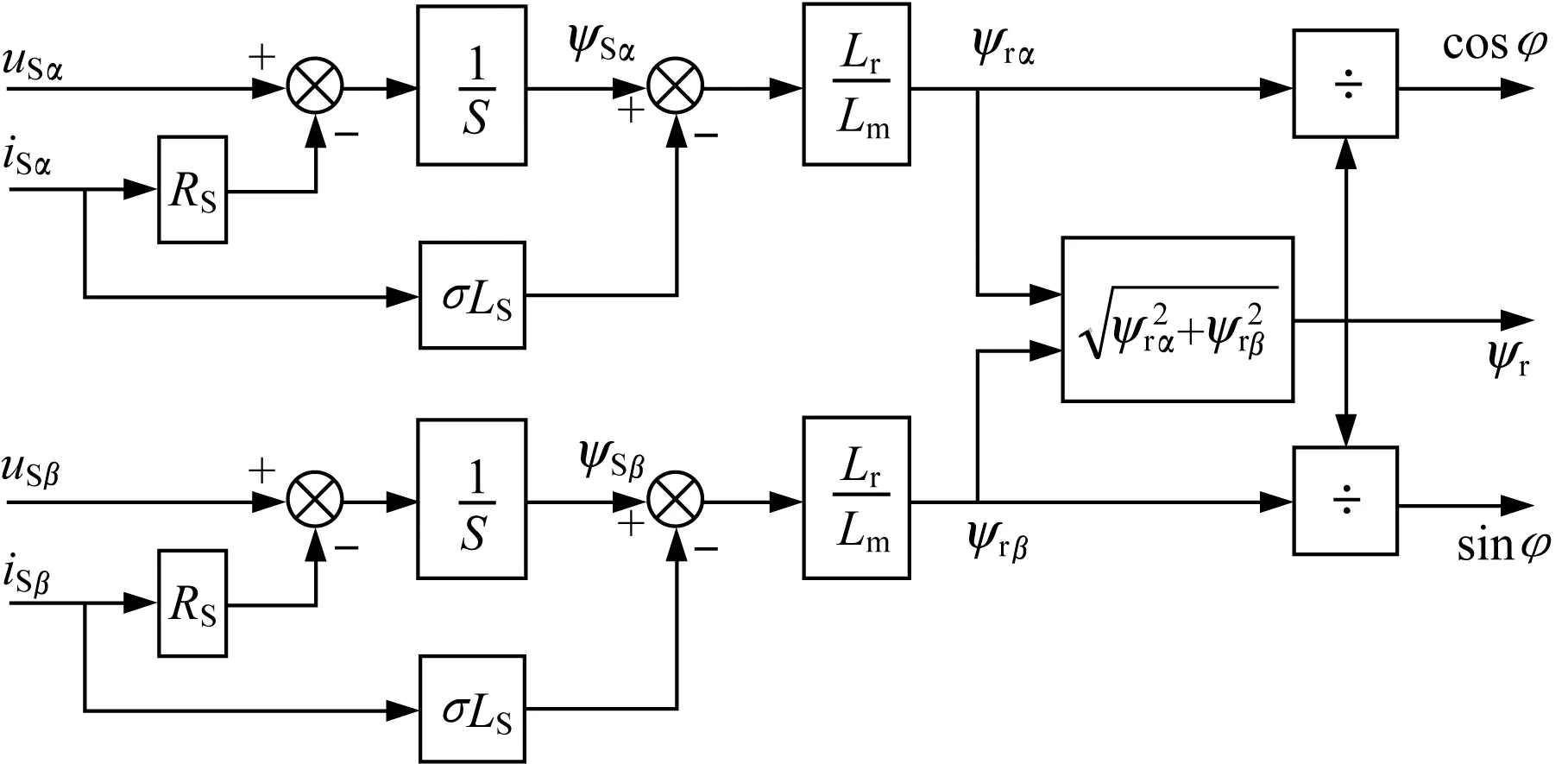
图3 转子磁链电压模型

该模型可转化为式(22):

(22)

式(22)中定子绕阻的阻值便于测量,在逆变单元静态识别的过程中即可完成。定子磁链与转子磁链可通过电压与电流值带入后进行计算,根据上节的推导将磁链带入运动方程得到电动机的输出转矩。该模型计算公式的积分环节也更适合中、高速电动机的转速控制,涵盖了炉辊电动机的工作参数。通过分析转子磁链的电压模型,可理解逆变单元控制电动机输出转矩的原理,为控制功能的实施提供了理论依据。

3 相邻炉辊间带钢受力

依据理论力学对相邻炉辊间带钢张力进行分析,力学基本定律中的胡克定律是现代物理学的重要理论,覆盖材料力学及弹性力学等多门学科。胡克弹性定律中定义[14]:弹力值ΔF等于倔强系数k与形变量Δx乘积:

ΔF=kΔx

(23)

推广至材料力学广义胡克定律,固体应力σ与应变ε成正比,比值系数为杨氏模量E,如式(24):

σ=Eε

(24)

其中,应变ε等于带钢t时间内长度变化量ΔL与初始时刻长度L0比值:

ε=ΔL/L0

(25)

假设两辊间应力σ0为0时,辊间带钢初始长度为L0,则当应力变化为σ时,带钢长度改变量为ΔL,综合上述两式可推导出:

σ=EΔL/L0

(26)

那么长度变化量:

ΔL=σL0/E

(27)

即带钢受力后长度变化量及受力大小,与初始长度及自身杨氏模量有关。那么炉辊间带钢张力大小,就应与炉辊间带钢初始长度、相邻炉辊沿带钢运行方向送入送出的带钢长度,即速度差相关。

继续换算相邻炉辊间带钢长度:

(28)

即相邻两辊间,带钢初始长度L0为:

(29)

沿带钢运行方向对于第n根及第n+1根炉辊间,初始距离及所受应力如下:

(30)

式中:Ln0为第n根和第n+1根炉辊不受外力下的带钢长度;Ln为当两辊间应力为σn时的长度。那么辊间带钢应力σn就应为:

(31)

(32)

式(32)反映应力变化量与该辊入、出口带钢长度变化量及入、出口应力相关,dLn=vn+1dt为第n辊出口长度变化量,dLn-1=vndt为入口变化量,式(32)可写成:

(33)

经整理得:

E(vn+1-vn)+vnσn-1-vn-1σn

(34)

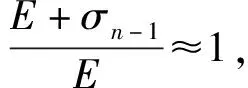
vn(t)σn-1(t)-vn-1(t)σn(t)

(35)

对式(35)两边进行拉氏变换:

(36)

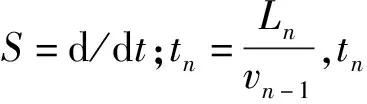
由式(36)继续推导,该段带钢单位张力为:

(37)

则转化为任意两相邻炉辊间带钢张力模型普遍式为:

(38)

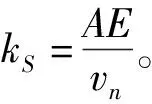
式(38)为相邻炉辊张力模型表达式,相邻炉辊n与炉辊n+1间带钢张力Tn为两辊线速度差值vn+1-vn与炉辊n入口张力Tn-1的一阶惯性环节输入量。增益系数kS为杨氏模量与带钢单位截面积乘积与炉辊n线速度比值。线速度反应炉辊转速,该系数可描述为炉辊n转速越大,向前输送带钢量越长,带钢松弛后炉辊出口方向张力越小。该模型改变了对辊类设备单独出力控制的方案,以相邻炉辊间张力为控制量,使相邻炉辊联动,提高张力调节的性能。图4为相邻炉辊带钢受力示意图。

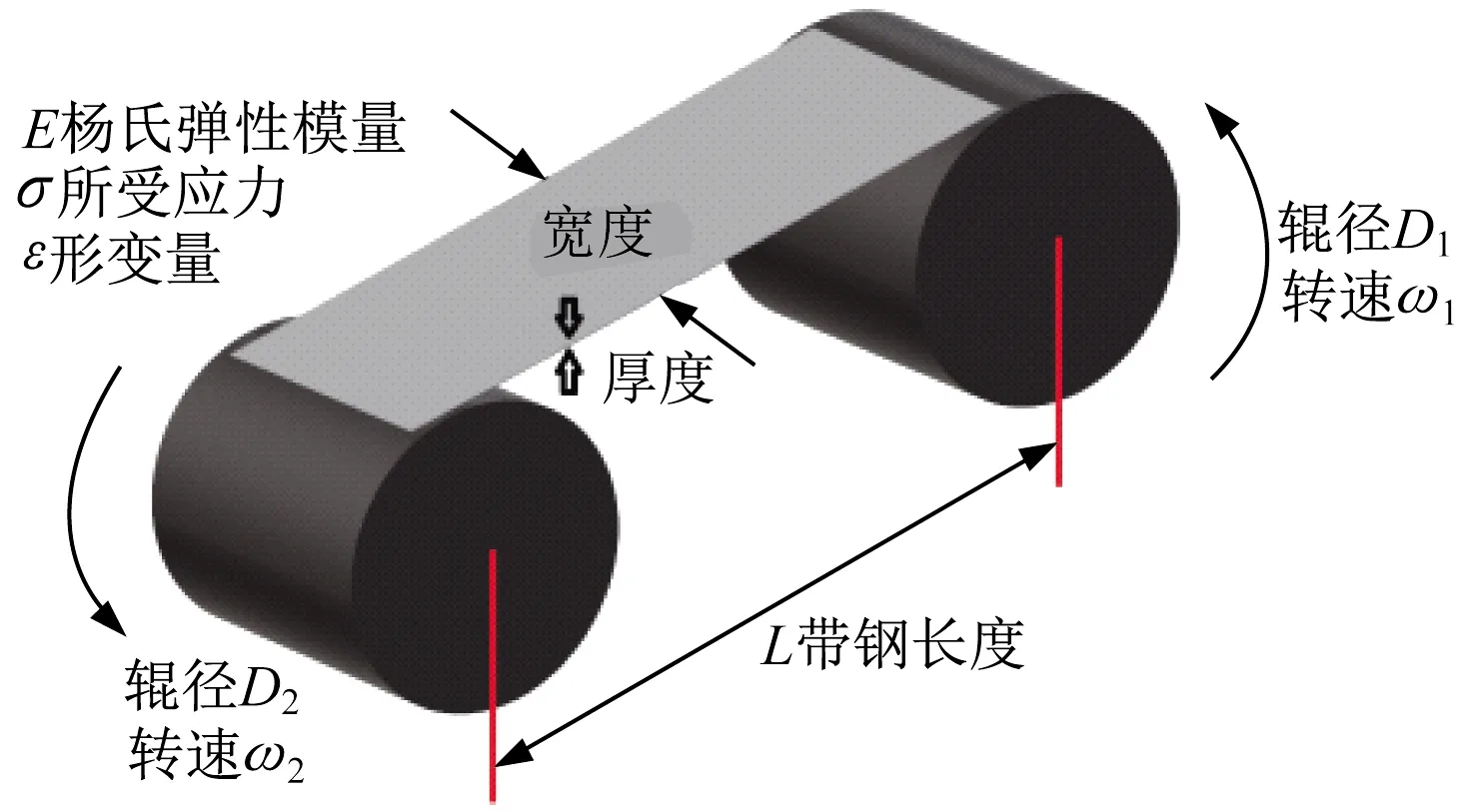
图4 相邻炉辊带钢受力示意图

4 结语

针对电气传动的控制与执行机理,结合张力产生的原理,借助交流电动机的等效电路,得到电流对电动机输出电磁转矩的作用。通过定子及转子矢量控制模型的研究,由空间坐标内的转矩方程,确认了定子、转子电流的耦合关系,以及负载转矩对电动机最终输出转矩的影响。在相邻炉辊间带钢受力模型中研究相邻炉辊转速速差与张力变化的关系,以及杨氏模量与退火炉温度变化的规律,为机组状态的维护提供了理论支撑。