基于集成学习算法的轨道几何状态短期预测模型

2021-05-09吕五一刘仍奎张秋艳吴霞

铁道建筑 2021年4期

吕五一刘仍奎张秋艳吴霞

（1.北京交通大学交通运输学院，北京 100044；2.中国铁道科学研究院集团有限公司电子计算技术研究所，北京 100081）

轨道几何状态是反映轨道质量的重要指标。轨道几何形位偏差过大会引起轨道不平顺，从而影响行车安全、行车速度和乘坐舒适性［1]。现阶段轨道交通运营企业对于轨道几何状态的管理比较粗放，维修管理模式主要以周期修、故障修为主［2]。通过科学的手段掌握轨道几何状态，准确预测其状态劣化趋势，可为管理者优化维修计划提供更智慧的决策支持，实现维修模式向预防修、状态修的转变。

轨道整体不平顺的评价方式为：采用轨检车每两个月对轨道的左右轨向、左右高低、水平、轨距和三角坑7 项轨道几何参数进行检测，计算每200 m 轨道单元的各单项轨道几何参数的标准差之和，即轨道质量指数（Track Quality Index，TQI）［3]。TQI 值越大表明轨道整体越不平顺，质量状态越差。各轨道交通运营企业的企业规范规定了相应的TQI管理值。如果某轨道单元区段的TQI 值低于相应的管理值，说明该区段整体轨道质量状态合格（TQI 合格），否则说明该区段整体轨道质量状态失格（TQI失格）。

目前，国内外对于轨道几何状态预测的研究主要可分为三大类，分别为机理类模型、统计方法类模型和机器学习类模型。

机理类模型主要是在轨道动力学等理论的基础上，通过室内模拟仿真试验研究车辆与轨道之间的作用关系来预测轨道几何状态。文献［4]建立了具有二系悬挂的车辆-轨道耦合动力学模型并与轨道下沉变形相联系，利用计算机仿真技术研究移动车辆荷载下轨道的累积下沉量和轨道状态变化来预测轨道不平顺的发展趋势。

统计方法类模型又可分为随机性统计模型和确定性统计模型。随机性统计模型将轨道几何状态劣化视为一个随机过程，通常基于轨道几何状态历史检测数据利用概率性方法构建轨道状态劣化预测模型。文献［5]考虑了影响轨道几何劣化的因素在轨道全生命周期内的不确定性，建立预测轨道几何劣化的贝叶斯模型。确定性统计模型通常利用回归分析等方法，基于轨道状态历史检测数据建立轨道状态与其影响因素之间的函数关系来预测轨道几何状态。文献［6]构建了轨道不平顺短期状态预测模型（TI-SRPM），对轨道单元区段相邻两次维修周期之间的未来一个轨检车检测周期内的各项轨道几何形位要素的每日峰值进行了预测。

随着大数据技术的发展，机器学习类模型被引入轨道交通基础设施管理研究领域。文献［7]利用主成分分析法分析了影响轨道几何状态的关键因素，并利用支持向量机（Support Vector Machine，SVM）、线性判别分析、随机森林等机器学习方法对轨道几何病害进行了预测。文献［8]利用人工神经网络和支持向量回归预测了直线和曲线上的轨距偏差值。

上述模型各有优缺点和独特的适用场景，由于影响轨道几何劣化的异质性因素较多，难以保证模型的普遍适用性。本文首先从概率分布方法、回归分析方法、机器学习分类方法三个不同的角度，分别利用Gamma 过程、二项logistic 回归、支持向量机构建三个TQI预测模型，然后利用Stacking集成学习算法将这三个模型进行组合，形成新的TQI预测集成模型。

1 建模思路

以200 m 轨道单元为研究对象，利用多次历史TQI 检测数据，预测其TQI 值是否会在下一次检测前劣化为失格状态。

集成学习的基本原理是构建并结合多个个体学习器来完成指定的学习任务。与单个学习器相比，集成学习器通常有更好的预测性能和泛化性能，即适用于新样本的能力。集成学习器预测效果的好坏取决于每个个体学习器的准确性和多样性。准确性是指个体学习器的预测精度。多样性是指各个体学习器之间应该存在一定的差异，即好而不同，从而实现不同个体学习器的强强联合及优势互补［9]。因此在构建集成模型时，选择概率分布方法、回归分析方法和机器学习分类方法来构建预测轨道区段不平顺质量状态的个体学习器，选择Stacking 集成学习法进行集成。Stacking 算法是Wolpert于1992年提出的一种集成学习算法［10]。不同于Boosting和Bagging等采用相同分类算法训练出单个学习器的集成学习算法，Stacking算法通过结合多种不同学习算法以保证个体学习器的多样性，往往具有更高的预测精度和更低的过拟合风险［11]。

模型整体结构如图1所示。

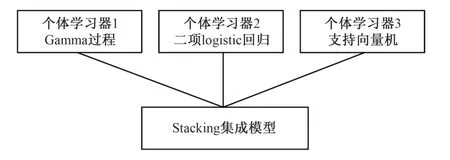
图1 模型整体结构

2 模型相关变量描述

为研究TQI 随时间的劣化程度，用变量ηT表示轨道单元区段检测时刻T时的TQI 合格或失格，变量ηT+1表示轨道单元区段检测时刻T+ 1 时的TQI 合格或失格，并根据轨道单元区段连续两次检测的TQI 值定义变量Y。ηT和Y的取值分别为

本文只考虑当前TQI 处于合格状态的某特定200 m 轨道区段是否会在未来一个检测周期内劣化为失格状态，Y=2 和Y=3 的情况不在本文研究范围内。因此，Y根据下一次检测时TQI合格或失格取值，即

处于不同位置的轨道单元区段，即使承受相同的列车荷载，其轨道几何状态的劣化规律也各不相同［1]。这是由于轨道几何状态的劣化受到众多因素的影响，包括轨道所在线路的地质类型、平纵断面、最大允许速度以及轨道的通过总重、轨道部件的规格型号等。以往的研究一般考虑异质性因素较少，例如只考虑通过总重等。本文为发挥机器学习处理高维数据的优势，在建模时充分考虑异质性因素的影响，选取曲线半径、最大坡度、道床类型、钢轨类型和是否处于加减速区段5种具有代表性的异质性因素作为轨道区段的特征属性，提高轨道几何劣化规律建模的准确性。

对于某200 m 轨道单元，设置模型构建所需的变量。

①X1：相邻两次TQI检测值的差。

②X2：当前TQI检测值与管理值的差。

③X3：轨道单元内最小曲线半径R的变换值。对于小半径曲线，即R≤800 m 时，取X3= 1-R/800；当R＞800 m时，取X3=0。

④X4：轨道单元内最大坡度G的变换值。X4=G/Gmax，Gmax为所有轨道区段中最大坡度值。

⑤X5：道床类型。对于整体道床，X5=1；对于碎石道床，X5=0。

⑥X6：判断钢轨是否为50 kg/m 钢轨，若是，则X6=1，否则X6=0。

⑦X7：判断钢轨是否为60 kg/m 钢轨，若是，则X7=1，否则X7=0。

⑧X8：判断轨道单元是否处于临近车站的加减速区段，若是，则X8=1，否则X8=0。

3 构建集成模型

3.1 Gamma过程预测模型

自1975年被引入可靠性研究领域以来，Gamma过程经常被用于描述严格单调的随机劣化过程，如磨损、疲劳、腐蚀等［12]。在本模型中，模型的输入变量为某200 m 轨道单元当前TQI 值与管理值的差X2，输出为下一次检测时失格（Y=1）的概率。

假设相邻两次TQI 检测值的差X1服从形状参数v＞0且尺度参数u＞0的Gamma过程{ }X1(t)，t≥0 ，t为TQI累积劣化时间，则其概率密度函数为

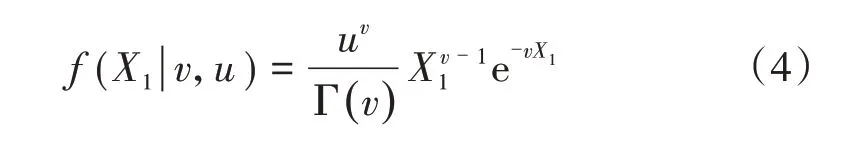
Gamma 过程{X1(t)，t≥0} 的均值和方差分别为E(X1) =v/u，V(X1) =v2/u。利用极大似然估计方法对参数v和u进行求解。假设X1的历史检测数据为x1k，k= 1，2，...，n，其似然函数Ln为

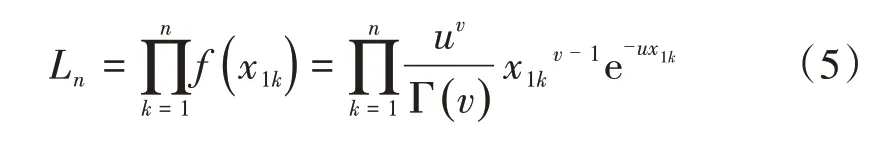
v和u的极大似然估计值由lnLn和lnLn解出。由此可以计算出当前状态为合格的某特定200 m轨道区段的TQI 在下一次检测时达到失格状态的概率P(Y= 1 )，即

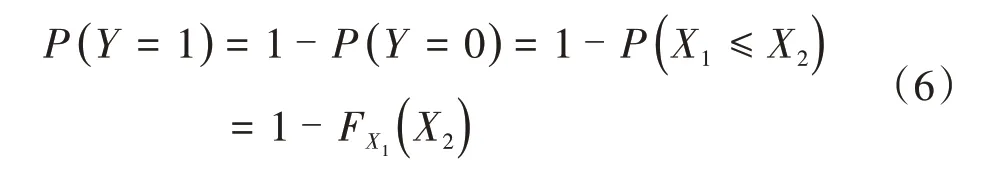
式中：FX1为Gamma过程的分布函数。

为构建集成模型，假设P(Y= 1)＞0.5时，Y=1。

3.2 二项logistic回归预测模型

二项logistic 回归模型属于概率型回归，作为广义线性回归模型的一类，主要用于描述和推断二分类因变量与一组解释变量的关系，在许多科研领域已得到非常广泛的应用［9]。利用二项logistic 回归输出0/1 值的特性构建logistic回归模型。模型输入为某200 m轨道单元的特征变量X2，X3，...，X8，输出为下一次检测时TQI合格或失格（Y）。模型表达式为

式中：β0为常数项；β2，β3，...，β8依次为变量X2，X3，...，X8的回归系数。

与Gamma 过程类似，利用TQI 历史检测数据采用极大似然估计法对logistic回归模型的参数进行估计。

3.3 支持向量机预测模型

支持向量机是在结构风险最小化原则和统计学习理论基础上提出的一种应用较为广泛的机器学习分类算法［9]。SVM的核心是要寻找最优的划分超平面(ω，b)，ω为划分超平面的法向量，决定了超平面的方向；b为位移项，决定了划分超平面与原点之间的距离，使得样本空间中距离超平面最近的训练样本到超平面的距离最大。当训练样本线性不可分时，SVM 可利用核函数将样本特征从原始空间映射到高维空间，使得样本在高维特征空间内线性可分，本文核函数采用径向基函数。为了有效避免过拟合，采用软间隔支持向量机模型以允许某些样本不满足约束。

模型的约束条件为

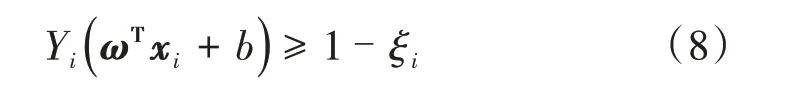
式中：xi为第i个样本的特征向量，xi=(X2，X3，...，X8)；Yi为第i个样本的标签

通过对训练样本进行学习，求解得出ω和b，而后输入X2，X3，...，X8，即可得到模型输出Y。

3.4 Stacking集成模型

Stacking 集成学习算法是一种常用的通过某个个体学习器来结合其余个体学习器的集成学习方法。被结合的个体学习器称为初级学习器，用于结合的个体学习器称为次级学习器。

Stacking 集成方法的基本原理是先利用初级学习算法和初始数据集训练出初级学习器，然后利用次级学习算法和初级学习器产生的新数据集来训练次级学习器。将初级学习器的输出作为新数据集中样例的输入特征，初始样本的标记仍然作为样例标记［9]。Stacking算法的伪代码参见文献［9]。

本文将Gamma 过程和SVM 作为初级学习算法，将二项logistic 回归作为次级学习算法，构建基于Stacking 的轨道几何状态短期预测集成模型。模型结构如图2所示。

图2 Stacking集成学习模型结构

4 实例分析

选取北京地铁1号线实测数据，对Stacking集成学习模型进行训练与测试。

北京地铁1号线上下行各31.04 km，共分为310个200 m 轨道单元区段。采集从2016年10月21日至2019年4月19日间的16 次TQI 检测数据和相应的线路设备数据，结合QB（J）BDY（A）XL003—2015《工务维修规则》规定的TQI 管理值（表1）对数据进行预处理，并剔除维修扰动的影响，得到4672 个样本。采用分层随机抽样，按照3∶1 的比例将样本划分成训练集和测试集。训练集包括3504 个样本，测试集包括1168个样本。

表1 轨道质量指数（TQI）管理值

模型的求解主要利用Python3.0 中的scikit-learn包来完成。选择分类正确率和接受者操作特性（Receiver Operating Characteristic curve，ROC）曲线下方的面积大小AUC 值（Area Under Curve）作为模型的评价指标。分类正确率表示被正确预测类别的样本数占样本总数的比例，体现模型整体的分类精度。AUC 值通常被用来判断二分类器的好坏，通过计算模型ROC 曲线下的面积得到。AUC 值综合体现出了模型的正例分类精度和反例分类精度，其取值一般在0.5 ～1，越接近1 说明学习器的分类效果越好［13]。利用训练集样本对所建立的模型进行训练学习，并对测试集样本进行预测，而后与实际历史数据进行对比，计算出模型预测结果的分类正确率和AUC 值。各模型的预测结果见表2。

表2 不同模型预测结果

从表2可以看出，Stacking集成模型的分类正确率和AUC值较其他模型均有显著提升。说明Stacking集成模型能够更加准确地预测TQI 变化趋势，同时具有更优的泛化性能。Stacking 集成模型能够较好地对短期的轨道几何状态进行预测，可以有效地辅助管理者针对安全风险高的轨道区段提前采取维修措施，从而保障轨道交通的安全平稳运行，为管理者更好地掌握轨道质量状态提供了一种新的思路。