西南山区铁路沿线反倾岩质边坡地震动力响应振动台试验研究

2021-05-09陈伟庚刘洋王栋岳茂张良

铁道建筑 2021年4期

陈伟庚刘洋王栋岳茂张良

（1.中国铁路广州局集团有限公司，广州 510000；2.中科（湖南）先进轨道交通研究院，湖南株洲 412000；3.中铁二院工程集团有限责任公司，成都 610031；4.西南交通大学土木工程学院，成都 610031）

西南山区铁路沿线地质构造复杂，地震活动强烈，由地震所引起的崩塌、滑坡等地质灾害频发。岩质层状边坡是铁路沿线分布极为普遍的边坡类型［1]。与堆积型边坡相比，该类边坡受到内部结构面的影响，稳定性较差，在地震作用下极易发生失稳破坏［2]，给西南山区铁路的工程建设及运营安全带来挑战。

国内外专家学者针对岩质边坡地震稳定性问题开展了大量研究。黄润秋等［3]结合现场实测成果建立了层状岩体失稳破坏模型，并通过大型振动台试验研究不同结构类型斜坡的破坏过程和地震响应特征；刘新荣等［4]针对三峡水库蓄水诱发的高频次微小地震，采用振动台试验与数值模拟相结合的方法，分析了不同动荷载、坡高等因素对顺倾层状岩质边坡的累积损伤和稳定性的影响；Fan 等［5]开展含泥夹层的顺层和反倾岩质边坡振动台试验，得到边坡动力破坏模式，并采用能量判识方法对边坡内部的震害损伤发展过程进行了分析。

以往文献对顺层岩质边坡的研究很多，对反倾岩质边坡的研究较少，并且这类边坡受岩土性质与内部构造的影响，在地震作用下的失稳破坏机制极为复杂。基于此，本文以西南山区铁路沿线典型的反倾岩质边坡为例，开展含结构面反倾岩质边坡的振动台试验，采用时频域分析方法研究输入不同峰值加速度地震波时该类边坡的地震动力响应特性，以供为西南山区铁路防灾减灾措施的制定提供参考。

1 振动台试验设计

1.1 模型参数的确定

本次试验以西南山区铁路一隧道出口处的反倾岩质边坡为原型，在信阳师范学院建筑与土木工程学院实验室开展振动台试验。该振动台为大型单向地震模拟振动台，振动台的台面尺寸为3 m × 3 m，台面结构为钢焊单层网格，台面最大承载量为10 t，最大振动速度为0.7 m/s，工作频率为0.1～50.0 Hz，位移范围为±125 mm，水平向最大加速度为15 m/s2。

根据相似理论，原型与模型的几何尺寸、土体重度和重力加速度的相似常数分别为10，1，1。通过Buckingham π 定理、量纲分析法［6]导出其余主要物理量的相似比，见表1。鉴于原型边坡岩性主要以石英砂岩夹板岩为主，参考模型试验常用的相似材料以及各种配合比相应的力学性能指标［7-8]，采用石膏、黏土、河砂和水作为原材料，岩层材料的配合比为石膏∶黏土∶河砂∶水=1.00∶5.38∶1.52∶0.27，结构面材料的配合比为黏土∶河砂∶水=1.00∶6.89∶0.25。通过密度试验、直剪试验以及三轴压缩试验，确定岩层材料的密度为1.908 g/cm3、黏聚力为15.5 kPa、内摩擦角为37.9°，结构面材料的密度为1.72 g/cm3、黏聚力为2.7 kPa、内摩擦角为41.7°。

表1 振动台试验物理量相似常数

1.2 模型制作及测点布置

模型箱由角钢、槽钢和钢板焊接而成，尺寸为2.0 m（长）× 2.0 m（宽）× 1.5 m（高）。为了便于观察边坡的变形破坏情况，模型箱两侧采用厚12 mm 的有机玻璃。同时，在有机玻璃与模型之间均匀涂抹凡士林，以减小模型与有机玻璃之间的摩擦。为了减少模型受边界效应的影响，在钢板与模型之间放置厚10 cm的聚乙烯泡沫作为减震层。

为了方便建立模型和试验分析，根据前期地质勘查结果将原型边坡简化为岩层平行的边坡，岩层倾角为35°，坡角为60°，按照岩层厚度6 cm、软弱夹层厚度1 cm 分层填筑夯实，填筑一层后静置一段时间后填筑下一层。填筑期间，将三向加速度传感器布置在坡体内部和表面，振动台的台面上也布置了加速度传感器。通过刚性支撑将拉线式位移计固定在模型箱上，用于测量坡面不同高度处的位移。

试验模型见图1，测点布置如图2所示，A1为坡肩测点；A2，A3，A4，A5 为坡体内部测点；A6，A7，A8 为坡体表面测点；A9 为台面测点，为计算边坡加速度峰值放大系数的参照点。

图1 试验模型

1.3 加载工况

在水平方向施加汶川卧龙地震波。施加前对地震波的峰值加速度进行归一化处理，持时按照原型和模型的相似关系进行调整。调整后的地震波加速度时程曲线及其傅里叶频谱见图3。峰值加速度从0.1g开始，按0.3g，0.5g，0.7g，0.9g，1.0g，1.2g逐级加载，并在每一级地震波加载前均对模型进行0.05g的白噪声扫描。

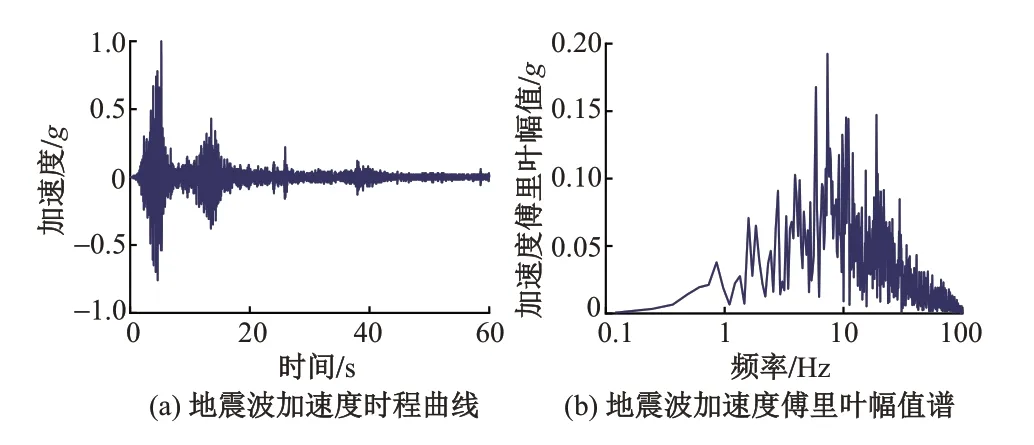
图3 调整后的地震波加速度时程曲线及其加速度傅里叶幅值谱

2 试验结果分析

2.1 反倾岩质边坡的加速度放大效应

将A1—A8 各测点的y向加速度峰值与振动台台面测点A9 的y向加速度峰值的比值定义为加速度峰值放大系数β。输入不同峰值加速度G的地震波时β值随边坡高度的变化情况见图4。可以看出：

1）对于坡内测点，输入G＝0.1g～0.9g的地震波时，测点A5—A4β值随高度增加而减小，测点A4—A1β值随高度增加而增大，特别是在2/3 高度（临界点A2）以上β值显著增大；输入G＝1.0g～1.2g的地震波时β值在临界点之前随高程增加而减小，在临界点之后β值显著增大。对于坡体表面测点，输入G＝0.1g～0.9g的地震波时β值随边坡高度增加一直增大；输入G＝1.0g～1.2g的地震波时测点A8—A7β值随高度增加而增大，测点A7—A6 呈减小趋势，在测点A8—A6变化幅度不大，但在临界点之后随高度增加又明显增大。可见无论是在坡内还是坡体表面，除局部β值随高度增加而减小，总体来看β值随高度增加而增加，表明地震动力响应具有高程放大效应［6]，且在坡肩处放大效应更明显。

图4 不同峰值加速度地震波作用下β 值随边坡高度的变化情况

2）在相同高度下输入不同G的地震波时，除了底部坡内测点A5 的β值大于坡体表面测点A8，其余同一高度的2 个测点均是坡体表面测点的β值大于坡内测点，反映出地震动力响应还具有趋表放大效应［6]。

3）坡肩测点A1 与临界点A2的β值相差较大。G＝0.9g时测点A1 的β值达到最大值，之后β值随G的增加而减小，可见加载到G＝0.9g时坡肩达到临界状态。此时坡体内部结构受到破坏，岩体中存在大量微裂缝，将边坡分割成松散块体，增强了边坡材料的滤波效应［9]。

2.2 反倾岩质边坡的加速度傅里叶幅值谱特征

对各测点的加速度时程曲线进行快速傅里叶变换（Fast Fourier Transformation，FFT），得到加速度傅里叶幅值谱。

输入G＝0.1g的地震波时反倾岩质边坡各测点加速度傅里叶幅值谱见图5。可见：在地震波作用下边坡坡内和坡体表面的加速度傅里叶幅值谱形态及分布基本一致。加速度傅里叶幅值主要分布在0～60 Hz，并在20，30 Hz 附近出现2 个峰值，并且幅值随边坡高度增加逐渐增大，表明地震波在向上传播过程中能量逐渐增大。

图5 输入G＝0.1g的地震波时反倾岩质边坡的加速度傅里叶幅值谱

对输入G＝0.1g的地震波时测得的台面测点加速度时程曲线进行FFT 变换，得到加速度傅里叶幅值谱。坡肩、坡内、坡体表面测点的加速度傅里叶幅值与台面测点的加速度傅里叶幅值的比值记为Spt［10]。

输入G＝0.1g的地震波时反倾岩质边坡的Spt变化曲线见图6。由图2 和图6 可知：①从A5 到A1，A8到A1，随着坡体高度增加，地震波穿越多个节理面，其频谱分布逐渐变得复杂，3个Spt峰值逐渐增大，高程放大效应明显。②坡肩测点A1 处Spt的峰值最大。这是因为坡肩为自由面，地震波在此处多次折射和反射使得SV 波（S 波为一种偏振波，其质点在竖直面内运动时称为SV波）与P波（纵波）发生了耦合效应。