膨胀土区桩承式路基土拱效应退化的数值模拟研究

2021-05-09徐子超何宗弈王一博田茂成郑亦轩潘高峰刘先峰

铁道建筑 2021年4期

徐子超何宗弈王一博田茂成郑亦轩潘高峰刘先峰，3

（1.西南交通大学土木工程学院，成都 610031；2.西南交通大学高速铁路线路工程教育部重点实验室，成都 610031；3.新疆工程学院土木工程学院，乌鲁木齐 830023）

膨胀土是一种高塑性黏土，具有吸水膨胀、失水收缩和反复胀缩变形特性。众多学者围绕膨胀土开展了大量的室内和现场试验。杨和平等［1]发现在首次干湿循环过程中，膨胀土会产生较大幅度的不可逆胀缩变形。陈伟志等［2]结合膨胀土土水特征曲线、渗透系数与吸力的关系曲线，采用线弹性PWP模型对路基的相对膨胀量进行了分析。Jiang 等［3]通过开展不同路基填高作用下膨胀土地基现场浸水和自然干燥试验，初步揭示了低矮路基作用下原状膨胀土地基的胀缩变形规律。杨果林等［4]对降雨作用下的微膨胀性路基膨胀行为进行了相关试验研究。

国内外不少学者对土拱效应的形态与发展、土拱所受影响因素亦进行了分析。庄妍等［5-6]通过数值模拟分析发现土拱效应受路基高度与桩间距的比值、土体性质等的影响。梁瑶等［7]通过自制土工试验仪模拟土拱效应证明了类似的结论，但其进一步发现在拱高的影响因素上，内摩擦角对其影响显著，黏聚力对其影响不大。桩土应力比也是评价土拱效应发展程度的一个重要指标。曹卫平等［8]均对桩土应力比的影响因素进行了研究，其中曹卫平通过试验研究发现桩-土相对位移在6～8 mm时，桩土应力比达到最大值。

以上研究对土拱效应与桩承式路基荷载传递的关系以及影响因素都进行了充分分析，但均未考虑膨胀土区土拱效应的演化过程。膨胀土地基在吸水膨胀、失水收缩的过程中会导致各种工程病害以及土拱形态的变化乃至退化的过程。

与非膨胀土区相比，膨胀土区桩承式路基荷载传递机理变得更为复杂，国内外学者对桩间土的膨胀模拟也仍较少，且对上拱规律的分析并不清晰。因此本文通过三维弹塑性有限元模型模拟桩间土体产生向上位移的方式探究土拱形态的演化规律，以期为后续模型试验提供指导，并对膨胀土区桩承式路基的长期稳定性和结构优化设计提供理论参考。

1 有限元模型

1.1 几何模型与参数选择

利用有限元分析软件ABAQUS 建立三维模型。地基土边界为1.1 m×1.1 m，厚度为0.4 m。路堤填土高1.05 m，共分7层填筑，每层厚度0.15 m。桩长0.4 m，地基土与路堤填土采用摩尔-库伦模型进行分析，桩采用线弹性模型进行分析。在桩与地基土、桩与路堤土、地基土与路堤土间建立接触面，法向接触设置为硬接触，切向接触设置为罚函数，罚函数中摩擦因数取0.445。各部分具体参数见表1。

1.2 模型的验证

将本文中路堤填料竖向应力随深度的变化曲线与文献［5]结果进行对比（图1），发现二者趋势相同，彼此平行。其中文献［5]的路堤高度为3.5 m，而本文填料高度仅为1.05 m，故竖向应力较小。这说明本模型是正确的。

表1 材料参数

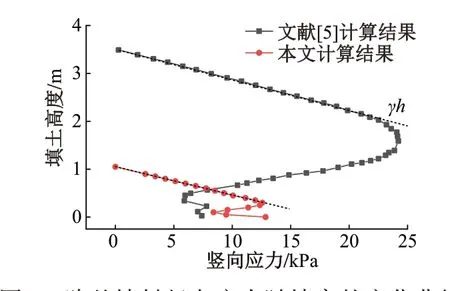
图1 路基填料竖向应力随填高的变化曲线

1.3 土拱退化模拟方法

分析过程主要分为两阶段，分别为土拱效应的形成阶段、退化阶段。为模拟膨胀土区4 m 填高的路基，在模型填筑阶段完成后在其上表面分步施加50 kPa的荷载。在土拱退化阶段，通过在模型底部施加向上的面位移的方式来模拟桩间膨胀土在膨胀过程中产生的向上位移，从而模拟土拱效应的退化过程。

2 计算结果与讨论分析

2.1 土拱形成阶段分析

2.1.1 基本数据

土拱形成阶段路基土分7层进行填筑。桩顶平面桩间土竖向应力与位移关系见图2。可知：距桩中心465 mm处，竖向应力随模型的填筑呈明显的阶梯形增加；距桩中心550 mm 处的桩间土竖向应力与沉降成正比。且距桩中心距离越远，竖向沉降越大，从距桩中心465 mm 至桩中心550 mm 处竖向沉降从0.089 mm增加至0.115 mm，增大了29.2%。

图2 不同位置桩间土竖向应力与沉降关系

填筑完成时桩中心剖面距桩顶不同位置处的沉降见图3。可知：在距桩顶0.15 m 处桩顶位移与桩间土沉降差异较大，差异沉降为0.02 mm。当距桩顶高度增加后，差异沉降逐渐减小。在距桩顶0.3 m 高度处，桩顶上方土体与桩间土上方土体沉降基本一致，即等沉面位置约在桩顶上方0.3 m 高度处。此高度为0.6倍桩间距，也就是土拱的高度。

图3 填筑完成时桩中心剖面竖向沉降

桩顶和桩间土竖向应力与差异沉降关系见图4（a）。可知，桩顶与桩间土的竖向应力与差异沉降成线性关系。将上述数据进行归一化处理后，得到图4（b）。其中，σs为竖向应力，δs为桩土差异沉降，γ为路堤填土重度，h为路堤高度，s为桩间距，a为桩径。桩间土竖向应力占自重应力的比值σs/γh表征了土拱效应的发挥程度。由图4可知：当路堤高1.05 m，桩间距0.5 m，形成完整土拱时，此时桩间土的竖向应力σs=13.978 kPa，桩间土差异沉降为δs=1.788 mm，此时σs/γh=0.75，δs/（s-a）=0.033。因此只需要较小的差异沉降就可以形成此工况下的土拱，使土拱效应充分发挥。

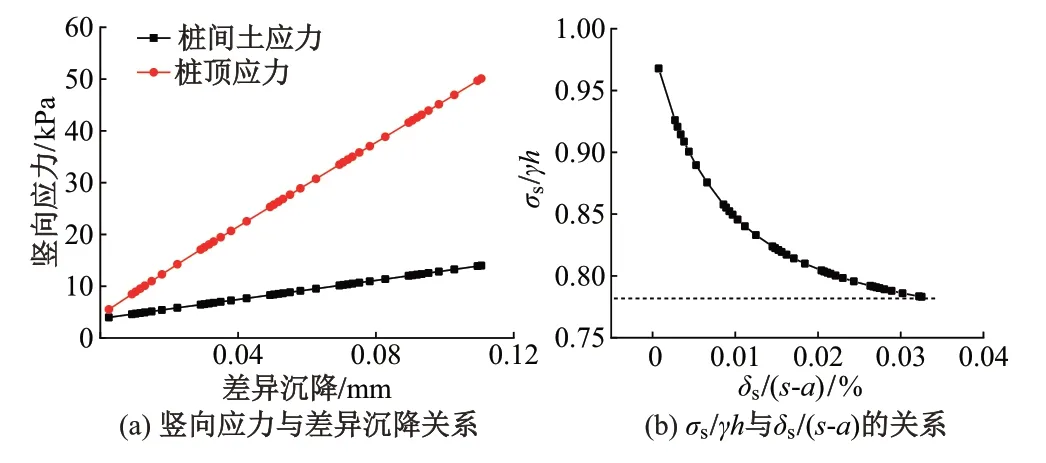
图4 竖向应力与差异沉降、桩间距的关系

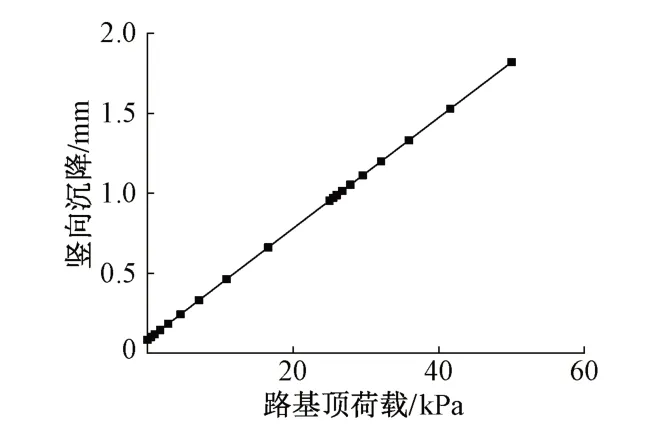
图5 路基顶面沉降与顶部荷载关系

填筑完成后，在模型顶部分级施加上覆荷载的过程中，路基顶面沉降与顶部分级施加荷载的关系见图5。可知：路基顶面沉降与顶部施加荷载成正比。当上部荷载施加至最大值50 kPa时，竖向沉降1.82 mm。

在模型顶部分级施加上覆荷载的过程中，桩间土、桩顶应力与顶部分级施加荷载的关系见图6。可知：当上部荷载施加至最大值50 kPa 时，桩间土竖向应力51.07 kPa，桩顶竖向应力为205.14 kPa。

图6 桩间土应力、桩顶应力与顶部荷载关系

2.1.2 土拱高度与土拱形成过程

为了解土拱高度，提取两桩平面中心线处的竖向应力，并与自重应力曲线进行对比。用竖向应力与自重应力曲线发生分离的位置确定土拱高度。中心线处竖向应力与自重应力的关系见图7。

图7 两桩中心处竖向应力分布曲线

由图7 可知：①竖向应力曲线大致可分为三个阶段。第一阶段，竖向应力沿填土顶面向下增加，在该阶段的初期，竖向应力的分布曲线与自重应力较为重合，曲线斜率为填土重度γ。第二阶段，竖向应力沿深度有所减小，减小的幅度越来越大。第三阶段，在曲线的末端，竖向应力又有所增加。这与文献［9]计算出来的土拱效应竖向应力规律相同。②在距离路堤顶面0.3 m 左右，竖向应力与自重应力开始分离，朝不同方向发展，因此判断此工况下土拱的高度为距离桩顶0.3 m处。

加载阶段桩中心剖面、距桩顶0.1 m 高平面处竖向应力见图8。可知：随着上覆超载的增加，应力云图逐渐相接，土拱效应逐渐显著。

图8 加载阶段桩不同位置平面的竖向应力

2.2 参数敏感性分析

2.2.1 桩间距对土拱效应的影响

参考文献［5]中桩间距与桩径之间的关系，本文中选取5 种桩间距进行分析，以探究不同桩间距对于土拱高度的影响。5 种桩间距分别为0.45，0.50，0.60，0.75，0.85 m。

根据不同桩间距的计算结果，绘制土拱高度随桩间距的关系，见图9。可知：随着桩间距的增大，土拱高度逐渐增加，桩间距从0.45 m 变化至0.85 m 的过程中，土拱高度H0增加了0.307 m，变化率为106%。这说明桩间距是影响土拱高度的重要指标。

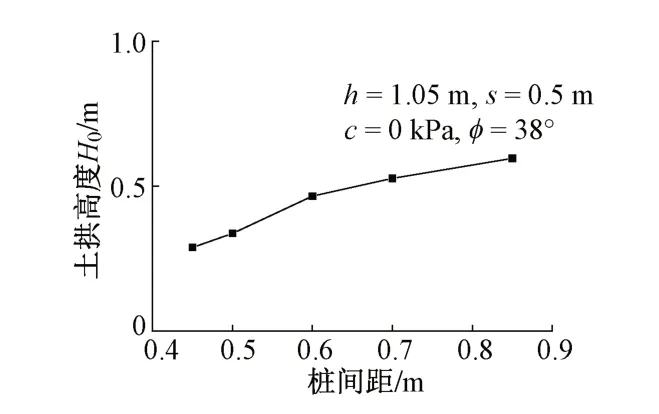
图9 桩间距对土拱高度的影响

2.2.2 填土强度指标的影响

土拱效应发生在上部路基填土中，因此要判断上部填土的强度指标对于土拱高度的影响。观察填土不同内摩擦角（20°，24°，30°，38°，45°）、黏聚力（0，30.0，45.0，58.9，100.0 kPa）的情况下的土拱高度，绘制摩擦角、黏聚力与土拱高度的关系，见图10。

图10 内摩擦角、黏聚力与土拱高度的关系

图10（a）给出了在路基高度h= 1.05 m，桩间距s=0.5 m 的情况下，土拱高度H0与内摩擦角的关系曲线。在选取的3 个内摩擦角的计算结果中，土拱高度随内摩擦角的变化较小，从20°至45°的过程中，土拱高度略微减小，土拱高度从0.361 m 减小至0.323 m，减小量为10.5%。图10（b）中也可看出随着路堤填土从无黏性土逐渐向有黏性土的变化中，即黏聚力从0 kPa增大至100 kPa 的过程中，土拱高度的变化同样并不明显，土拱高度仅从0.348 m 下降至0.343 m，变化率仅为1.7%。由此可以判断，虽然填土强度会对土拱效应产生一定的影响，改变填土强度指标会改变土拱高度，但不是影响土拱高度的最重要的指标。

2.3 土拱退化阶段分析

采用前文所提及的在模型底面施加面位移的方式进行土拱效应退化阶段的模拟。对高度h=1.05 m，桩间距s= 0.5 m 的路基，讨论了在全过程（路基分层填筑、上部加载、模型底部施加反向位移）中土拱效应的演变、桩土应力比与差异沉降的变化关系。

2.3.1 土拱效应的演变

在填筑阶段随着填土高度增大，土拱效应逐渐产生，桩间土压力逐渐减小，桩逐渐承担上部荷载。因此σs/γh较好地描述了土拱效应的发挥程度。δs/(s-a)为桩土差异沉降的归一化处理，将桩土差异沉降与净桩间距（桩间距减桩径）对比，讨论σs/γh与δs/(s-a)的关系。根据土拱效应发挥阶段，σs/γh与δs/(s-a)的比值逐渐减小，推断在土拱效应退化阶段，桩间土竖向应力占自重应力的比值应不断增大，即σs/γh的值将增大，故σs/γh与δs/(s-a)的值应逐渐增大。但这只是初步的判断，因此本文提取σs/γh与δs/(s-a)的值绘制关系曲线，讨论土拱退化阶段二者的关系。

全过程阶段σs/γh与δs/(s-a)的关系见图11。可知：分层填筑阶段与施加上部荷载的阶段，当σs=51.07 kPa时，土拱效应充分发挥作用且达到稳定，σs/γh最终稳定在0.75，说明此时桩承担了大部分上部荷载，土拱效应充分发挥。随着模型底部面位移的施加，σs/γh最终为0.96。证明在模型底部施加面位移后，桩间土所承担的荷载逐渐增加，土拱效应发生退化。

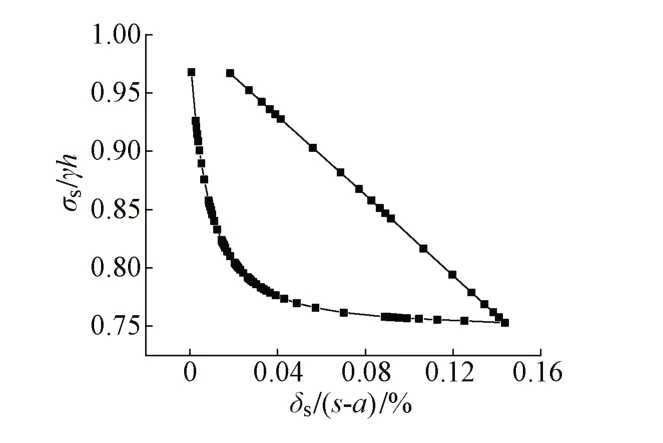
图11 全过程阶段σs/γh与δs/(s- a)的关系曲线

2.3.2 桩土应力比随差异沉降之间的关系

桩土应力比是衡量土拱效应发挥程度的重要指标。全过程阶段桩间土应力、桩顶应力与差异沉降的关系，以及桩土应力比随差异沉降的关系见图12。可知：①在填筑阶段与上覆荷载施加阶段，桩土应力比逐渐增加。当上部超载加至50 kPa 后，桩土应力比达到稳定，稳定值为4.02。说明土拱效应在这个过程中已经充分发挥作用。②随着模型底部面位移的施加，桩顶应力从205.14 kPa减小至80.33 kPa，桩间土应力从51.07 kPa 增大到65.58 kPa。此时，桩土应力比从4.02减小至1.22。说明由于位移荷载的施加，由桩所承担的荷载变为逐渐由桩间土承担，土拱效应发生弱化。

图12 竖向应力、桩土应力比与差异沉降的关系

2.4 土拱退化阶段分析

土拱退化阶段桩中心剖面竖向应力图与距桩顶0.1 m 高平面处竖向应力见图13。可知：随着底部反向位移的施加，桩顶上部土的应力逐渐减小，土拱逐渐消失，其作用逐渐减弱。

图13 土拱退化阶段桩不同位置平面竖向应力

由图12，图13可知：当反向位移逐渐增大后，桩土应力比逐渐减小。

将桩土应力比作为评价土拱效应的一个重要指标来描述土拱效应的退化程度。为讨论土拱效应的退化程度，定义退化比例的概念。计算施加不同反向位移值时桩土应力比大小，将路基顶部荷载施加完成时桩土应力比作为初始值，计算不同桩底位移值工况下的桩土应力比，将两者差值与初始值的比值作为土拱效应的退化比例，其中桩土应力比初始值为3.58，见表2。

由表2 可知：当模型底部位移为0.9 mm 时，桩土应力比减小至1.22，桩土应力比的退化比例为65.9%，此时土拱效应大幅减弱。