习题变式在小学数学中的应用
2021-05-08李继辉
李继辉
【摘 要】 在日常教学中发现,教师使用的习题较为单一,缺乏层次性和创新性,习题的内涵和功能的开发较不足,习题与知识本身的联系也比较单薄,未能达到提升学生思维的效果,本文结合具体习题变式案例,阐述了习题变式的作用,创新的题型有助于拓宽学生的思维空间,加强知识与习题之间的联系,提升学生的思维能力,培养学生的创新思维。
【关键词】 习题变式 思维提升 创新能力 应用
习题是日常教学中师生每天都要接触的教学用具,学生通过习题进行巩固和提升,教师通过习题了解学生对新知识的掌握程度,从而调整教学进度和改变教学方法,但从平时的教学中发现师生对于习题的应用上存在以下现状:
1. 学生就题练题,只着眼于题目的解答,对题目中考察的知识没有进一步的理解,对于知识的内涵没有更深层次的思考,思维定势较为明显;
2. 教师对习题的使用普遍较单一,基本以课本或练习册的习题为主导进行讲练,习题缺乏灵活性,教师没有对习题进行深层次的挖掘,忽略了习题的价值;
3. 习题的创新性不足,导致学生的思考范围过于狭隘,对习题与知识的联系理解不透彻,从而弱化了习题的功能。
从以上存在的现状可以看出,习题变式在小学数学教学中是非常有必要的,通过习题变式可以为学生呈现类型迥异的题型,提供给学生不同的解题思路以及思考方向,帮助学生感受习题与知识的关系。本文将从以下两点阐述习题变式的应用:
一、计算习题要重视算理的渗透
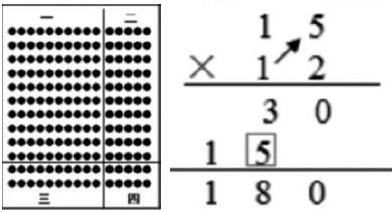
计算教学是小学阶段“数与代数”领域中最为重要的环节,计算教学是小学数学教学的基础,新课标降低了对一些运算的复杂性、技巧性和熟练程度的要求,反而更重视学生对算理的理解,因此对于计算教学,我们不能只停留在算法上的讲解,还应在习题上渗透算理,使学生通过习题掌握算法,理解算理。例如在人教版三年级下册两位数乘两位数的教学中,常见的习题大多是笔算:23×34、78×82,纠错题的形式,或者从解决问题中进行计算训练,这几种习题的练习基本上只包含了算法的训练,完全忽略了算理的渗透,我们需要对这种题型进行变式,如下题:一包糖果有15颗糖,小明妈妈买了12盒,一共有几颗糖果?在以下图中,方框中的5与点子图对应的部分是( )。
A. 一
B. 二
C. 三
D. 四
以上习题的题型是选择题,载体则是解决问题,主旨是不再让学生过分的注重算法的训练,通过习题引导学生对算式和点子图进行分析,在计算教学中要重视算理的内化,通过习题变式,将算理渗透在习题当中,帮助学生理解算理,从而巩固算法。
二、运算定律习题要注重思维的提升
运算定律是小学阶段“数与代数”的重要组成部分,新课标要求学生要学会探索规律,发现规律,而不是死记结论、死套公式和法则,因此,我们在教学中,除了要在课堂教师中让学生充分参与课堂,探究运算规律,也要对课后习题进行变式,让学生通过习题感受运算定律的原理,提升学生运用定律的灵活性。例如在四年级下册乘法运算定律的教学中,对于乘法分配律的教学,习题设计大多以熟练使用定律为主,如简便计算:99×38+38,17×23-23×7,88×125,類似的题目大多以运用乘法分配律为主,容易导致学生针对题型进行死记硬背,将几种特殊的简便计算进行记忆,从而死套公式,因此我们需要对习题进行变式,例如:
小明在计算两位数乘两位数时,先算45×8=360,再算45×20=900,最后计算360+900=1260,小明计算的这道题是( )。
A. 45×82 B. 45×20
C. 45×28 D. 25×48
通过简单的变式,将乘法分配律隐藏在题目的条件当中,学生做题时需要将乘法分配律从题目中剥离出来,发现两位数乘两位数的计算过程就是乘法分配律的使用过程,突出前后知识的联系,从而让学生切实感受到知识与习题之间的联系,提高习题的巩固作用。
再如:小明在用计算器计算49×78时,但是按键“9”不灵了,还可以这样算( )。
A. 78×50-1 B. 78×40+78×9
C. 78×7×7 D. 50-1×78
此题将乘法运算定律与计算器的使用结合,体现数学知识与生活实际的紧密联系,新课标强调通过现实情境使学生体验、感受和理解“数与代数”的含义,通过习题变式,我们能够很好的将生活实际与数学联系起来,让学生在习题中感受生活中处处存在着数学,数学不是独立而枯燥的学科,从而提升学生学习数学的兴趣。数学习题的设计应注重习题的层次性,通过提升习题的思考量,为学生提供思考的空间,进而提升学生的数学思维。
创新意识是新课标中十大核心概念之一,也是学生数学能力中最难培养的。创新意识不仅要在数学课堂中培养,也要在学生的课后练习中渗透,而这样的渗透便需要教师的习题引导,教师对习题的创新能够带动学生的思考,间接的影响学生的数学思维,潜移默化的提升学生的创新能力,因此,作为教师,我们需要精心设计习题,在习题中培养学生的数学综合素质,提升学生的应用能力。
