考虑不确定性的并网型微电网容量优化配置

郭 宇, 吕红芳, 王冰昆

(上海电机学院 电气学院, 上海201306)

微电网[1-2]是结构为源 储 荷构成的一个相对独立的小型供电系统,具有自治功能。它是解决分布式电源接入大电网,且最大化实现能源利用率的方法之一。微电网容量优化[3-4]是根据用户所在地的地理位置和条件、气象资料、负荷情况、分布式电源工作特性、供能需求及系统设计要求等数据确定微电网各组成部分的类型和容量。

容量优化会很大限度地影响微电网内各微电源之间是否协调工作、微电网系统功率是否保持平衡,而且很大程度上决定整个系统的供电质量和经济收益。因此,微电网容量优化配置研究是在微电网设计和建设之前就应关注的问题之一。关于并网型微电网的容量配置优化问题。文献[5]结合可再生能源的随机性和符合预测的随机误差构造微电网的不确定性模型,采用混合整数规划法实现各分布式电源和储能系统的容量配置,保证微电网设计成本最低的目标。文献[6]通过SCK 鲁棒线性优化方法将不确定性模型转化为确定性模型,采用NSGA-II求解多目标优化配置问题。文献[7]将韦布尔分布和MLE-ER 方法结合,提出新的风电出力概率密度函数,并以此为基础研究了风机机组的组合方式。

并网型微电网作为研究主体,上述众多研究中还存在的问题是需要巨大的样本数据,才能使估计出的结果与真实分布存在较小偏差,而这又会带来巨大的计算量。因此,本文通过多状态建模的方法,仿真出风机、光伏系统出力和负荷可能发生的所有状态。仿真结果作为描述风机输出功率、光伏输出功率和负荷随机性的数据。通过并行遗传算法求得考虑不确定性因素的容量配置结果,与没有考虑不确定性因素的配置结果在随机场景下进行对比,验证本文所述方法的合理性和有效性。

1 并网型微电网多状态建模

本文的研究主体是风光储并网型微电网,其中风速和光伏受自然环境影响,具有强不确定性的特点。风机和光伏系统能以不同的输出功率状况运行,按其输出功率可以将其分为多个不同的性能状态,而负荷可以将其当作是输出功率为“负”的电源。因此,并网型微电网内各分布式电源工作过程中会存在不同的性能水平,再加上负荷的波动性,使得整个系统呈现出多种状态特征。对于这种因为不确定性所呈现出的多状态系统,本文采用多状态理论对风、光和负荷不确定性进行建模,针对性地考虑系统中可能出现的不确定性因素。

1.1 风力发电功率的多状态建模

风速的概率密度分布满足韦布尔分布,当风速介于切入风速vci和额定风速vcr之间时,将此区间的风速分为NW个状态,通过最优离散划分方法分得风速概率分布的最优分位点ni(i=1,2,…,NW),则

式中:r为矩阵阶数;f(v)为风速的概率密度函数。

当风速小于切入风速vci或大于切出风速vco时,记为第NW+1个状态,此时风机出力为0;当风速介于额定风速vcr和切出风速vco时,记为第NW+2个状态,此时风机出力为额定功率。各状态下发生的概率为

式中:FW(i)为第i个状态发生的概率。

综上可计算出每个仿真时刻风力发电系统各状态下的输出功率和其相对应的状态概率。

1.2 光伏发电功率的多状态建模

太阳辐照度的概率密度分布满足贝塔分布,当辐照度介于最低辐照度Gmin和额定辐照度GS之间时,将此区间的风速分为NG个状态,通过最优离散划分方法分得太阳辐照度概率分布的最优分位点g j(j=1,2,…,NG),即

式中:f(G)为太阳辐照度的概率密度函数。

当辐照度小于最低辐照度Gmin时,记为NG+1个状态,此时光伏发电的功率为0;当辐照度不小于额定辐照度GS时,记为第NG+2个状态,此时光伏发电系统以额定功率输出。各状态下发生的概率为

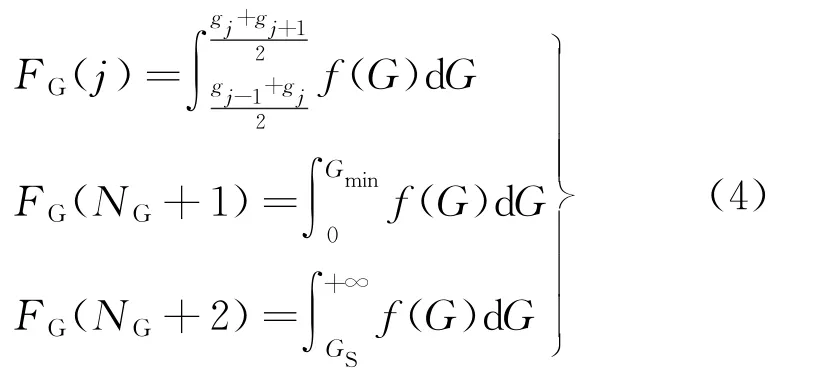
式中:FG(j)为第j个状态发生的概率。

综上可计算出每个仿真时刻光伏发电系统各状态下的输出功率和其相对应的状态概率。

1.3 负荷功率的多状态建模

负荷分布近似服从正态分布,而正态分布的范围据研究约99.73%的数值在距离平均值3个标准差之内,故假设各个时刻的负荷分布在距离该时刻负荷平均值的3个标准差之内,即

式中:PL(t)为t时刻的负荷功率;μL(t)为t时刻的负荷平均值;σL(t)为t时刻的负荷标准差。

利用最优离散划分方法得到负荷的最优分位点c k(k=1,2,…,NL,NL为负荷区间内的状态数量),对应状态发生的概率为

式中:f(PL)为负荷的概率密度函数;FL(k)为第k个状态发生的概率。综上可计算出每个仿真时刻内负荷各状态的大小和与之相对应的状态概率。

分别对各个状态进行仿真,包含风机、光伏和负荷可能发生的所有状态。将风、光、负荷连续的不确定性状态按照其分布规律处理为多个离散的确定性状态,这样既能避免冗杂的计算,也能避免预测所带来的误差。

2 并网型微电网的容量配置优化模型

2.1 目标函数

系统的年平均经济成本Cc由平均每年设备购入成本Cb、平均每年运维费用Co和平均每年设备更换费用Cch三部分组成,即

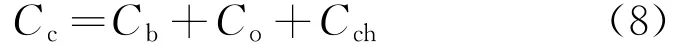
平均每年设备购入成本是指微电网内各电源设备购入总费用乘以资金回收系数[8]ηcrf 之积,即

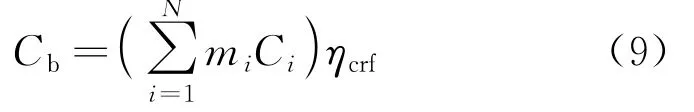
式中:i=1,2,3分别对应微电网中风机、太阳能电池板和储能装置;Ci为各类微源设备的单价;m i为各类微源的数量;ηcrf 为资金回收系数,指在预定的回收期内,按复利计息的条件下,每年回收额相当于投资额的比率。

微电网各微电源的运行维护费用一般分为固定成本和可变成本。其中固定成本Cf是指设备的人工成本,而可变成本Cv是指可变的维护费用,平均每年运维费用可以和第一年的运维成本形成一定的关系,即

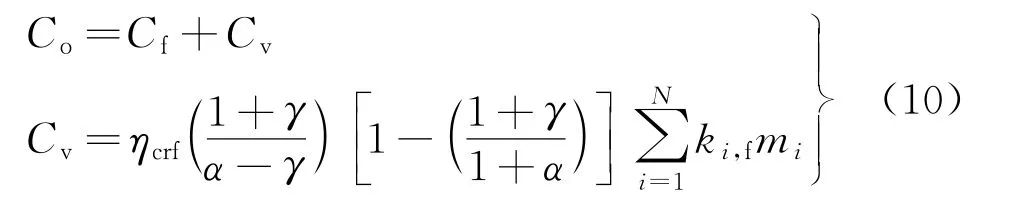
式中:γ为年通货膨胀率;α为实际利率;k i,f为各类微源的运维成本费用系数。

平均每年设备更换费用与各类微源的设备使用寿命有关,即

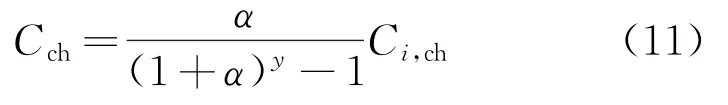
式中:y为系统的设定使用年限;Ci,ch为第i种分布式电源的单个置换费用。

考虑了不确定性因素后,利用条件风险价值(Condition Value at Risk,CVaR)将微电网的运行风险转化为平均风险损失,加入上述年平均经济成本函数中。微电网的运行风险主要指风光负荷的不确定性导致微电网可能出现的缺电损失概率和负荷损失,通过CVaR建立风险度量模型Q(λ,x,ζ(i)),结合年平均经济成本,建立考虑风光、负荷随机性的不确定性容量优化模型。基于多状态建模的不确定性容量优化模型的目标函数为

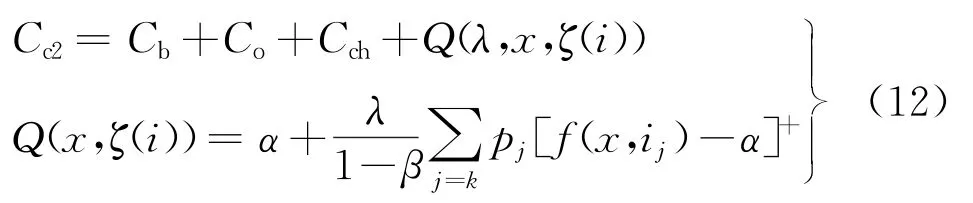
式中:λ为风险系数,数值越大表示考虑风险成本越多;x为决策变量,即微电网中各微电源的数量;i为随机变量,即风速、辐照度和负荷;ξ(i)为各随机变量对应的概率密度函数;β为置信度,取值范围为[0,1];α为置信度是β时的风险价值VaR值;[x]+=max([0,x]);f(x,i j)为随机变量i的状态j;p j为状态j发生的概率。

2.2 约束条件

(1) 各类微电源安装数量约束。在进行优化配置时,安装各类微电源须考虑系统的占地面积约束,即

式中:Nwt、Nwt,max为风机数量和最大安装数量;Npv、Npv,max为太阳能电池板数量和最大安装数量;Nb、Nb,max为储能电池数量和最大安装数量。

(2) 系统功率平衡约束为

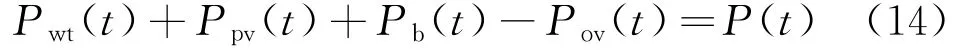
式中:Pwt(t)、Ppv(t)、Pb(t)分别为风机、光伏和储能电池在th的输出功率;Pov(t)为微电网系统在th内的溢出功率。

(3) 蓄电池能量约束为

式中:S(t)为电池的荷电状态;Pdg、Pcg、PN分别为蓄电池放电功率、充电功率和额定功率;η为电池转换效率,取0.2;Smin、Smax为蓄电池荷电状态的上下限,取0.2和0.8。

(4) 系统容量缺额率约束。为使微电网系统能抵消风光、负荷的随机性带来的波动,保证供电可靠性,需要设置容量缺额率进行约束,即

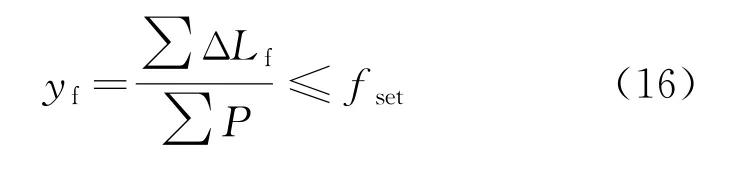
式中:ΔLf为运行时间内的电量缺额;fset为系统设定的容量缺额率限制;P为当前输出功率。

2.3 模型求解

并行遗传算法[9](Parallel Genetic Algorithm,PGA)是将遗传算法的天然并行性和计算机的高速并行计算相结合,具有良好的并行搜索能力和收敛精度。不确定性框架下的容量优化模型所需处理的数据庞大复杂,PGA算法可有效解决这些问题。因此,本文对算法的初始种群数目设定为50,目标函数最大连续不下降次数选取20,最大迭代次数选取500,精度要求Δ≤e-15,求解流程如图1所示。

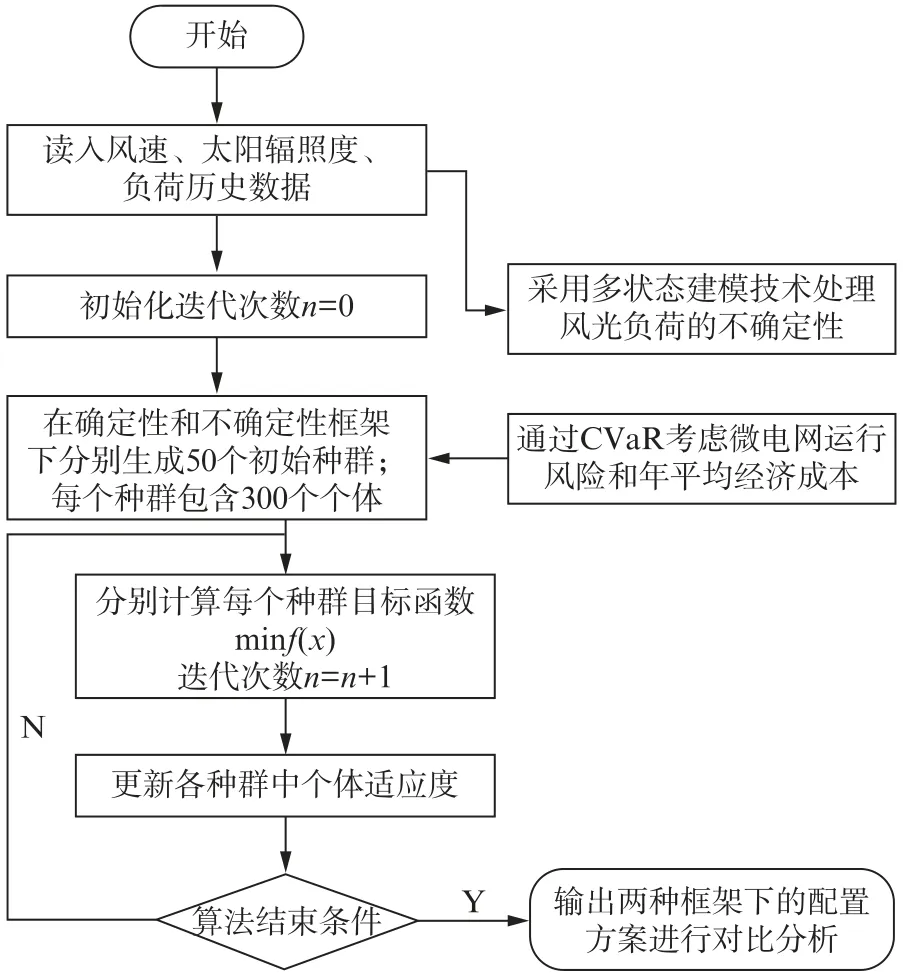
图1 求解算法流程

3 算例仿真和结果分析

3.1 原始数据

本文并网型微电网优化配置的气象模型采用的是全年每小时的气象数据,数据从中国气象数据中心获得。以某地2018年风速、日照度和负荷作为输入数据,其中风速测量间隔为每3 h,观测高度为5.5 m;日照度测量间隔为天;负荷测量间隔为每小时,记录时间为全年8 760 h。

2018年该地区的总用电量约为1138.37 kW·h,选取风光储能并网型微电网,各分布式电源分别为风机(WT)、光伏电池(PV)、全钒液流电池(VRB),具体参数[10]如表1所示。

表1 各电源设备参数

3.2 评价指标

本节将介绍负荷损失风险指标和自平滑率这两个指标,以便更直观地比较不同配置方案之间的不同。

(1) 负荷损失风险指标(Load Loss Risk,LLR)。描述负荷损失的发生概率和负荷损失的严重程度[11],即

在现实情况中,切除过多负荷或功率缺额过大证明了微电网的可靠性不高,即LLR值越高可靠性越低。因此,LLR 值与微电网的可靠性呈反相关趋势。

(2) 自平滑率δ。描述并网型微电网的运行过程中,公共连接点(PCC)上功率的波动情况,可以反映在不确定性因素影响下导致的功率波动,对电网稳定性的影响[12-13],即

式中:n为系统运行总时刻;Pli为第i个时刻PCC节点处的功率;为运行周期内PCC节点处的平均功率。

在运行过程中,δ越大,说明在该时刻公共连接点处有较大的功率波动。过大的功率波动会限制微电网接入大电网。

上述两个指标可以有效地描述考虑了风光、负荷随机性情况下的配置结果对微电网运行可靠性的影响。

3.3 不确定性容量优化模型的求解策略

首先选取并网型微电网中风机台数Nwt、光伏电池台数Npv和储能电池个数Nb为优化变量,然后将风速、辐照度和负荷进行多状态建模。分别以风速3 h、太阳辐照度1 d、负荷1 h为时间步长,每月份构造一个典型日,每个典型日取风速的多状态划分数量NW=8,太阳辐照度的多状态划分数量NG=6,负荷的多状态划分数量NL=6,进行多状态建模,通过仿真可以直观地看出风电、光伏和负荷不确定性的特点。

针对基于多状态建模的微电网不确定性容量优化配置模型,采用PGA 进行求解,得到相对最优解集A。为了验证多状态建模方法的合理性和有效性,针对同一算例,将目标函数Cc2中考虑不确定性运行风险的风险度量模型Q删除,得到确定性模型下的目标函数。设置相同的运行约束条件、控制策略和迭代方式进行仿真实验,同样采用PGA 算法进行求解,得到另一个相对最优解集B。最后将两个解集在10个随机场景下进行验证,对比其负荷损失风险指标LLR值和自平滑率δ。

3.4 构造随机场景

系统实际运行时的风速、太阳辐照度、负荷与历史数据相比,必定存在着误差。为了比较分析考虑不确定性因素和未考虑不确定性因素下配置方案的区别,需要对两种方案在不同的风光出力场景下进行对比,因此本节采用拉丁超立方采样方法[14](Latin Hypercube Sampling,LHS)模拟出多个风光出力场景,然后通过同步回代削减得出具有代表性的随机风光场景。

首先通过LHS方法分别对风力和光伏发电两种场景进行随机抽样,抽样规模共计N=2 920个数据(全年8 760 h,每3 h采样一次),共有N2个数据场景;然后通过同步回代的方法,去除所有数据场景中差异度小的场景;最后保留10个有明显区分度的数据场景,得到的随机场景1的第1周的风速和第1个月的辐照度与历史场景对比如图2所示。

3.5 结果分析

在Matlab平台上验证本章所提出的不确定性容量配置模型的有效性和合理性。通过LHS方法和同步回代方法设定最后得到的随机数据场景数量为10。风险系数[15]λ在[0,1]之间表示不同的风险情景,本节只考虑两种模型在一般情况下的配置结果对比分析,故λ取0。

采用PGA 算法分别对微电网不确定性容量优化模型和确定性优化模型进行求解,其配置结果如表2所示。其中方案1为考虑了不确定性的配置方案,方案2为确定性框架下的配置方案。

就配置结果来看,方案1中风机和光伏电池的安装数都多于方案2,而储能电池的安装数量少于方案2。不确定性电源的容量增加,有更大的冗余度来填补风光负荷波动所带来的电量缺口。相比在确定性配置框架下,若风光、负荷发生随机波动时,需要更多地依靠储能系统和外部电网来满足功率缺额,这会大大增加设备的使用频率,增加维护和更换费用等。

在随机数据中验证两种配置方案下的运行性能,比较两种配置方案优劣的指标如表3所示。

从LLR指标来对比两种方案,可见从确定历史场景到随机场景,方案2的LLR值总是比方案1要大,说明方案2在面对风光负荷的不确定性波动时,微电网系统所要承担的负荷损失概率也越大或者负荷损失更为严重。由此可知,考虑了不确定性的优化配置方案在面对风光负荷的波动时,所需承担的停电概率更小,表明方案1具有较强的鲁棒性和供电可靠性。

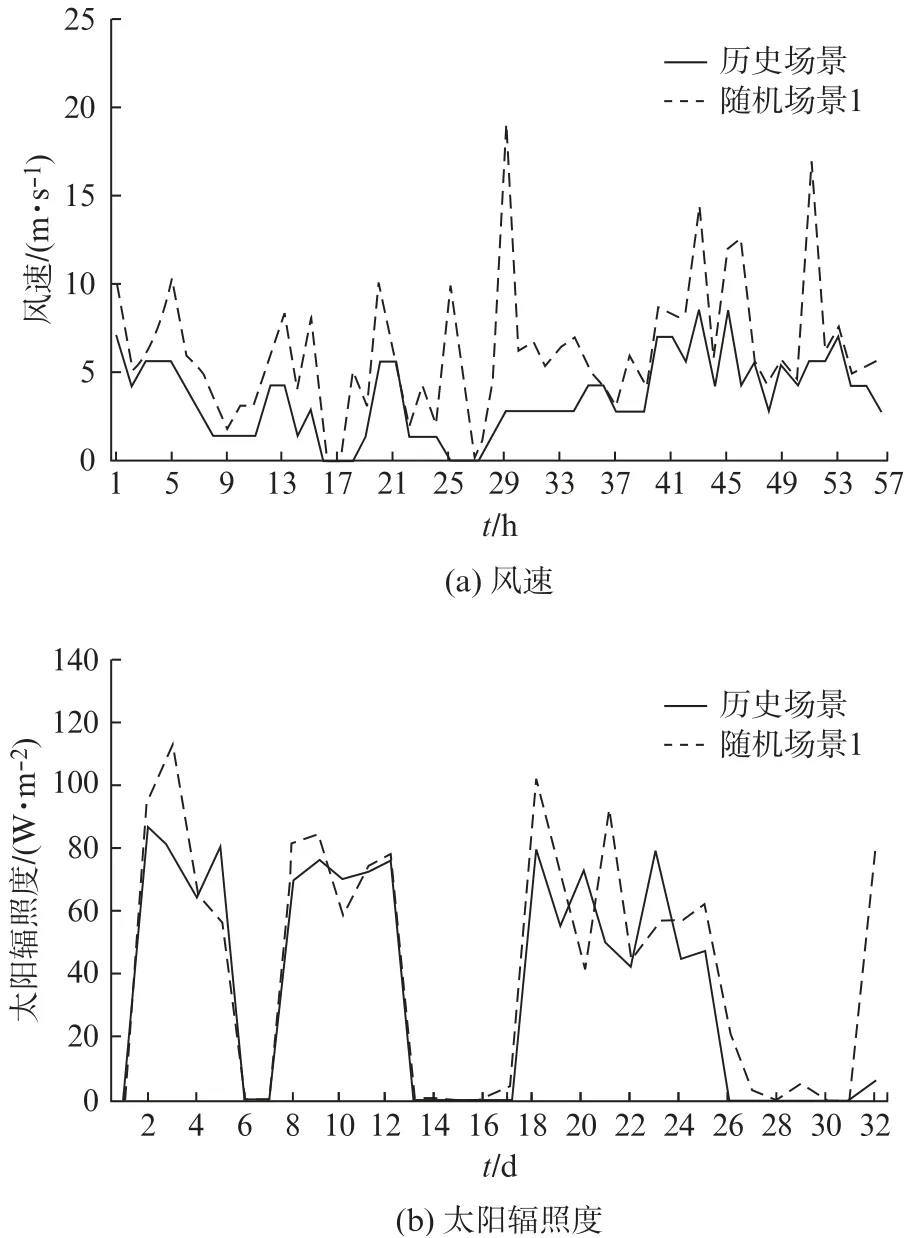
图2 历史场景与随机场景1的风速、辐照度对比

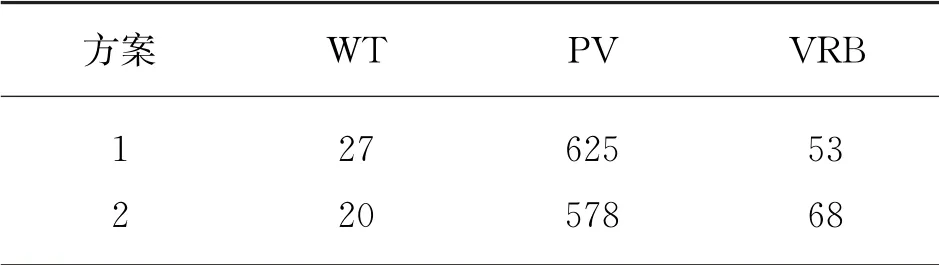
表2 两种模型的配置结果

表3 两种方案在随机场景下的运行指标对比

从自平滑率指标来对比,同样地,方案2的自平滑率值总比方案1的大。该指标描述的是功率的波动情况,数值大,说明在确定性配置方案下面对风光负荷的波动时,因为没有足够的冗余度,需要靠储能系统来抑制功率的波动,所以带来的结果较差。而方案1因为可再生能源有足够的冗余,所以在面对波动时,能够有效地减少系统本身所带来的功率波动影响。

综上所述,从系统运行可靠性和微电网并网能力出发,方案1下的优化模型得到的配置结果可以在面临多个突发情况下都能保证良好的供电可靠性,并且不会对大电网产生较大的波动,因此,考虑了不确定性因素的配置方案的鲁棒性更高,在实际运行过程中抗干扰能力更强。

4 结 论

本文利用多状态建模理论处理风、光、负荷的不确定性,考虑不确定性带来的运行风险,建立以经济成本最低为目标函数的数学模型,通过PGA求解得到相对最优配置方案。将其与确定性优化模型下的配置方案在不同的随机风光场景下进行对比分析,验证了考虑不确定性因素所得到的容量优化配置方案具有更高的鲁棒性,可削弱随机波动对微电网系统本身带来的可靠性影响。