考虑SVC 和储能接入电网的多目标协同经济调度

高林， 成龙， 张聪， 唐海国， 邓威， 任磊， 罗波

(1.湖南大学， 湖南 长沙410082；2.国网湖南省电力有限公司电力科学研究院， 湖南 长沙410007；3.国网湖南省电力有限公司检修公司， 湖南 长沙410004)

0 引言

近年来， 随着能源危机和环境污染问题日益突出， 可再生能源发电得到迅猛发展， 其中以风电技术的发展最为迅速。 由于风力发电易受自然环境和时间等因素的影响， 其功率输出具有较大的波动性和间歇性， 因而大规模风电场并网给电力系统的运行、 调度以及控制等带来一系列的影响。 而储能系统(energy storage system， ESS) 能量响应速度快，可以快速吸收或者释放电能， 能够有效地平抑分布式风电的波动性[1-2]， 从而提高电力系统对分布式能源的消纳能力。 因此， 利用储能系统平抑风电功率波动的经济调度的研究具有重要的意义。

国内外学者在ESS 参与风电并网的经济调度方面已开展了大量的研究， 并已逐渐受到学者的重视。 文献[3] 建立了考虑风电波动并能跟踪电网调度要求的经济调度模型， 并采用NSGA-Ⅱ算法进行求解， 综合评估系统的总成本、 能量缺失率和功率的波动量； 文献[4] 为平抑可再生能源输出功率的波动， 提出了一种储能动态充放电控制策略； 文献[5] 提出了一种基于经验模态分解的储能经济调度优化模型， 并通过仿真验证其具有平滑风电功率波动的作用。 以上文献是基于储能减小风电功率随机波动进行的经济调度的研究， 对于风电并网引起的系统电压稳定和电压波动问题没有考虑在内。

静止无功补偿器(static var compensator， SVC)能快速灵活地对系统进行无功补偿， 有效控制电压波动， 同时改善电压稳定性[6]。 文献[7] 通过在电网中加装SVC 提高风电并网系统的运行经济性和电压质量， 以网损效益、 投资维护费用和电压偏移为目标函数， 采用遗传算法求解； 文献[8] 建立了综合污染气体排放量、 配电网总费用和系统电压偏差的多目标模型， 并利用自适应多目标粒子群算法求解； 文献[9] 提出了配合无功优化的经济调度模型， 采用理想点法将多目标优化问题转化为单目标优化问题， 有效降低线损和发电成本； 文献[10] 采用SVC 对风电场进行无功补偿优化， 研究风电场并网点处配置SVC 最佳补偿量问题； 文献[11] 提出了以一种SVC 最优选配方案， 以有功能耗费用、 SVC 安装费用、 柴油发电机无功生产费用为目标函数， 确定各状态下SVC 最优安装位置，目标函数中没有考虑电网的安全运行指标。

在以上研究的基础上， 为兼顾电网的安全性和经济性， 通过在电网中加装SVC 和储能装置来减小系统的综合运行成本以及改善系统的电压质量。本文充分考虑风电和储能系统的运行特性， 引入SVC， 建立兼顾电网安全性和经济性的多目标经济调度模型， 对有功调度和无功调度进行协同优化[12-13]， 获取使系统电压偏差、 网损和运行成本均为最小的最优解， 最后与权重系数法分析获得的Pareto 前沿面进行对比分析， 验证所建立模型的可行性。

1 SVC 的工作原理

SVC 是柔性交流输电系统 (Flexible AC Transmission Systems， FACTS) 中典型的并联补偿装置， 其基本功能是从电网吸收或向电网输送可连续变化的无功功率， 使装设点的电压保持在一定范围内[14-15]。 SVC 的种类多种多样， 但基本元件离不开晶闸管投切的电容器 (thyristor switched capacitor， TSC) 和晶闸管控制的电抗器(thyristor controlled reactors， TCR)[16]。

SVC 只能交换无功功率， 不能交换有功功率，因为其内部只包含无源元件。 在稳态情况下， SVC的电源型等值电路[17-19]如图1 所示。 SVC 的电源型等效电路是由可控电压源和输入导纳串联组成。

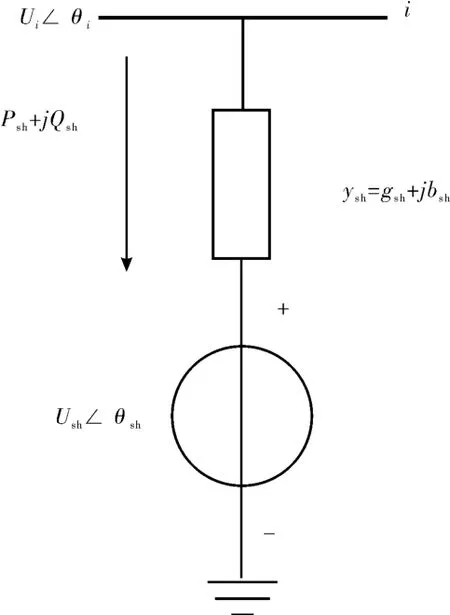
图1 SVC 的模型

当SVC 接入系统时， 此时的潮流方程形式如式(1) (2):

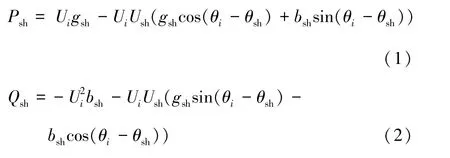
式中，Psh为SVC 的内部有功功率；Qsh为SVC 装置提供的无功补偿； Ui为SVC 接入节点i 的电压；Ush为SVC 的内部可控电压源的等效电压； ysh为SVC 内部的等效输入导纳， 且ysh=gsh+jbsh， 其中gsh和bsh分别为输入导纳的实部和虚部； θi为节点i 的电压相角； θsh为SVC 内部可控电压源的电压相角。

考虑SVC 内部交换功率时自身不消耗有功功率， 应附加SVC 内部的有功功率等式约束以及其他约束条件:

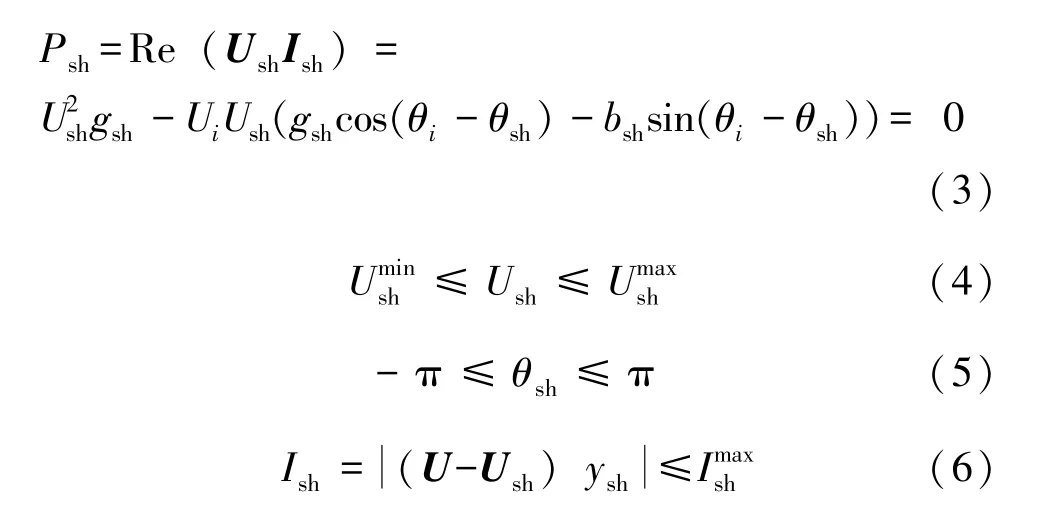
本文利用SVC 灵活地向电网提供无功补偿的原理， 实现控制母线电压的恒定， 即:

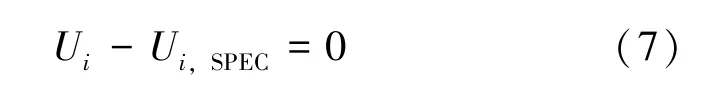
式中， Ui，SPEC为在节点i 装设SVC 的指定电压幅值。

2 考虑SVC 和储能装置接入的多目标经济调度模型

风电出力和负荷的波动性是影响电力系统稳定性的重要因素， 为保证配电网的安全稳定运行， 考虑SVC 和ESS 参与配电网运行调度系统降低综合运行成本， 同时改善配电网的电压质量和减小网损， 建立基于上述目标的经济调度多目标优化模型， 可以为配电网的调度运行提供经济、 技术上的双重评判标准。

2.1 考虑储能系统接入的有功调度优化模型

由于储能系统在促进风电消纳、 平抑风电波动和削峰填谷具有较好的效果， 因此为提高电力系统消纳风电和减少环境污染， 风电接入电网后的经济调度模型应在传统的电力系统经济调度模型基础上考虑减小弃风成本和环境污染费用。 因此， 含风电场的有功经济调度目标函数为:

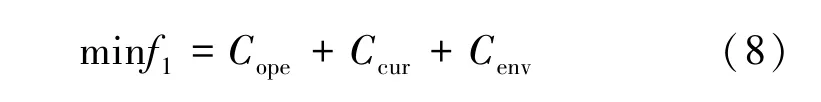
经济目标包含发电机组的发电成本、 弃风惩罚成本以及环境污染费用。 配电网运行的总费用f1计算公式为:

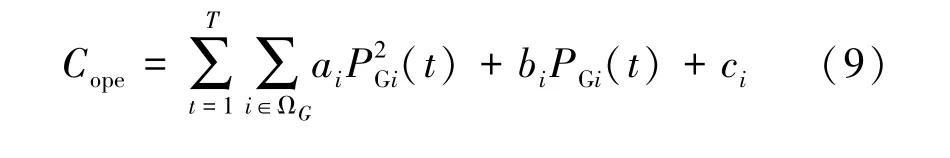
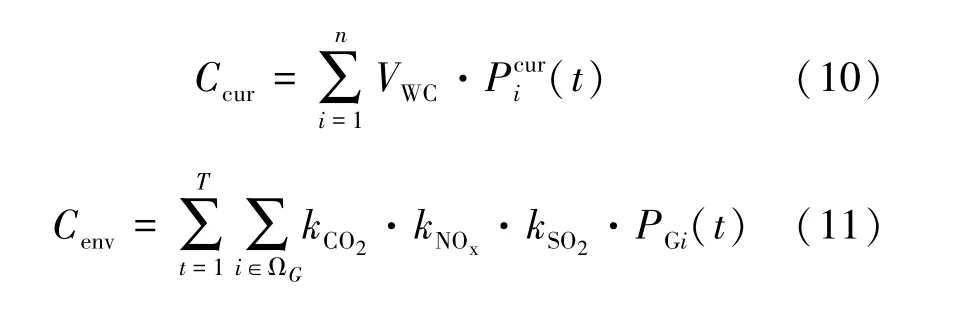
式中， T 为当前调度的时段数； ΩG为发电机组集合；Cope为配电网的日运行成本； Ccur为弃风成本；发电机组的发电成本和机组出力为二次函数关系，其中ai、 bi和ci分别为第i 台机组的成本系数，PGi(t) 为第i 台发电机t 时段的有功出力；VWC为弃风惩罚系数，为弃风功率； Cenv为环境污染费用[20]； kCO2、 kNOx和kSO2分别表示二氧化碳排放系数、 氮氧化合物排放系数以及二氧化硫排放系数， 单位均为元/MW。

2.2 考虑SVC 提高电网安全运行的无功优化模型

无功优化是假设发电机有功出力和负荷已知，考虑单一调度时段或某一时间断面电网无功资源分配和电压控制， 通过调节相关控制变量包括变压器变比、 无功补偿和发电机端电压， 保证电网稳态运行安全和电压质量最高。 模型如下:

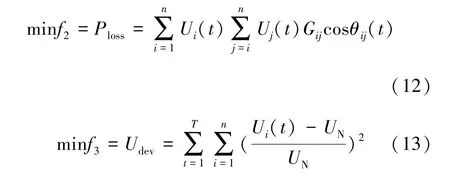
式中，Ploss为系统的网损； Gij是节点导纳矩阵第i行、 第j 列的实部；θij(t) 为t 时段节点i、 j 间的相角差；Udev为电压偏差； Ui(t) 为第i 个节点t 时段的电压幅值； UN为额定电压。

2.3 多目标经济调度模型的约束条件

多目标经济调度模型需要考虑的约束条件包括系统功率平衡约束、 潮流方程约束、 各机组出力上下限约束、 机组爬坡速率约束、 线路传输功率限制、 节点电压安全约束等。

1) 系统实时功率平衡方程

电力系统的发电和用电功率必须保持平衡， 功率平衡是维持电力系统安全稳定运行的基础。 一旦电力系统的功率失去平衡， 就会直接影响系统的电能质量， 因此必须设立功率平衡方程。

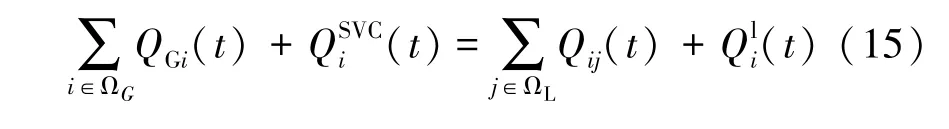
2) 潮流方程等式约束

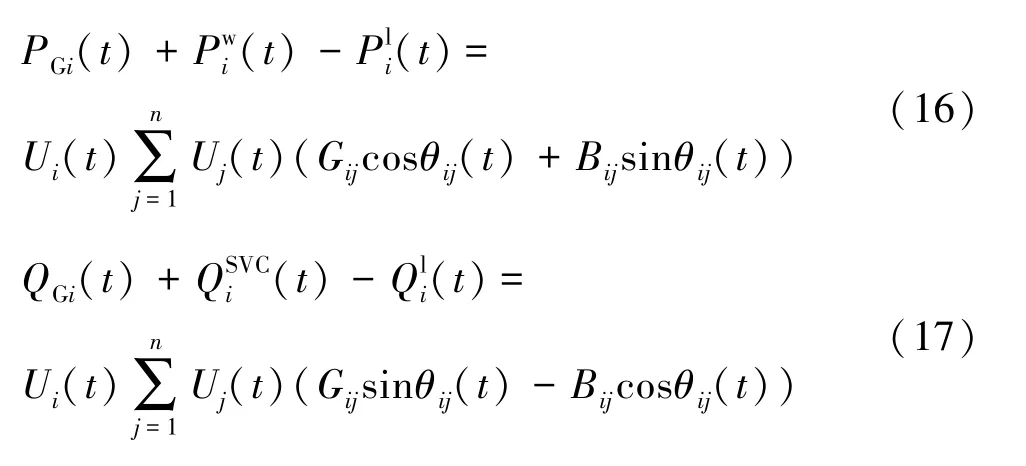
式中， Gij和Bij分别为节点导纳矩阵中的第i 行、 第j 列元素的实部和虚部。

3) 风、 火电机组出力上下限约束

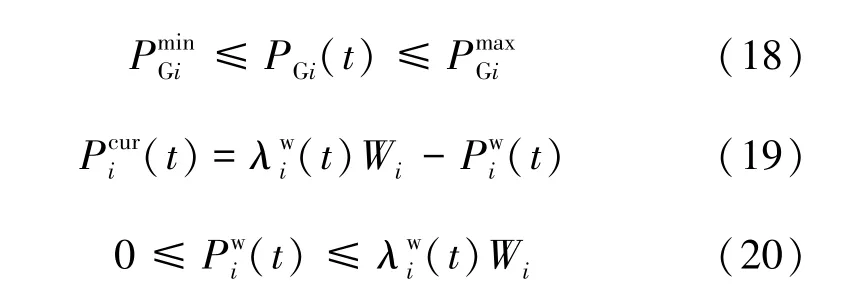
4) 发电机组爬坡速率约束

5) 输电线路潮流约束

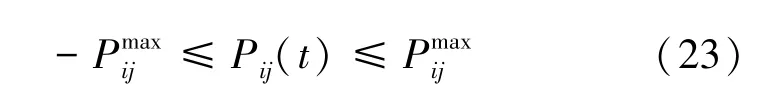
6) 电压上下限约束

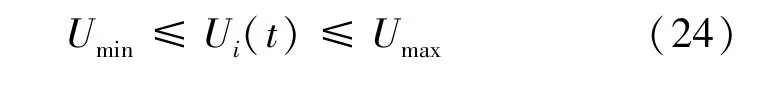
式中， Umin和Umax分别为节点电压幅值的下限和上限。

2.4 储能系统的模型

储能电池装置在电网中应用广泛， 具有安装地点灵活、 能量转换效率高等优势[21]。 本文利用荷电状态(state of charge， SOC) 衡量电池储能系统的运行状态， 其模型表示为:

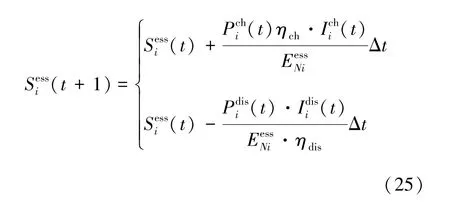
为避免充放电冲突， 储能充、 放电状态需要满足如下要求:

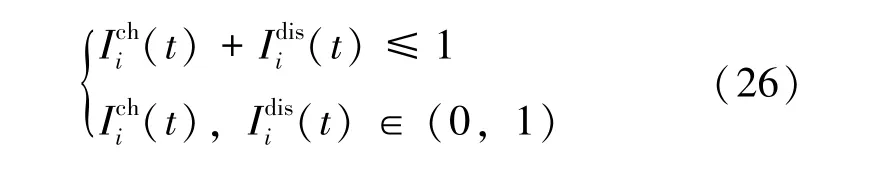
ESS 在运行过程中的功率和容量需要满足如下约束:

1) 储能系统充、 放电功率的限制

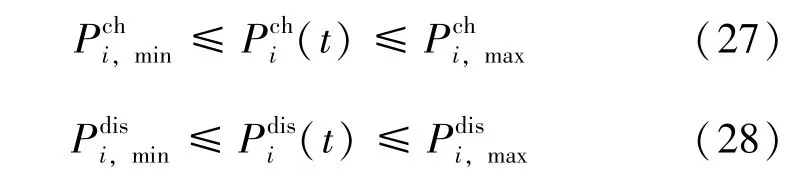
2) 储能系统的能量储存限制

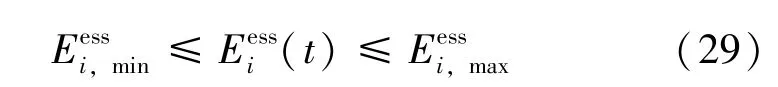
3) 储能系统的荷电状态约束

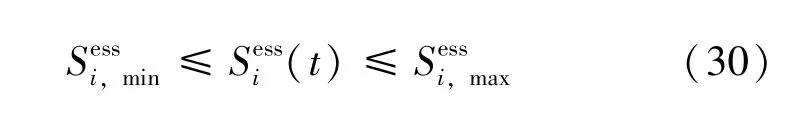
为保证储能电池的持续工作能力， 需要保证每天调度始与调度末的SOC 一致， 故优化过程还应满足如下约束:

将建立的多目标经济调度模型同储能以及SVC模型结合起来， 采用协同迭代方式[22]进行优化求解， 分析储能减小风电功率波动以及SVC 调整系统电压的作用。

3 多目标协同优化算法

多目标优化问题的模型一般可以表示为:

式中， x 为控制变量； fk(x) 为优化目标向量；gi(x)为不等式约束条件； hj(x) 为等式约束条件。

对于经济调度模型， 采用多目标协同优化算法进行求解， 算法步骤如下:

第一步， 设置迭代精确度ε 和最大迭代次数kmax， 并且令k=0；

第二步， 初始化发电机的机端电压和SVC 的无功补偿；

第三步， 进行有功调度的优化， 通过控制发电机组的出力以及储能系统的充放电功率， 优化系统运行成本f1；

第四步， 将上一步中有功调度优化所得到的各机组有功出力以及储能的输出功率作为无功优化的初始参数， 控制发电机的机端电压以及SVC 装置的无功容量， 进而优化系统的电压偏差f2以及网损f3；

第五步， 将第四步无功优化模型中计算的发电机机端电压和SVC 的无功补偿再次作为有功调度新的初始参数， 进行优化计算， 再次获得新的系统综合运行成本；

第六步， 将第五步获得的机组以及储能装置的输出功率， 再次作为无功优化模型的新输入参数，计算新的发电机组机端电压和系统网损；

第七步， 分别计算第三步和第五步的系统综合运行成本之差的绝对值， 即， 计算第四步和第六步的电压偏差之差的绝对值， 即；

多目标协同经济调度流程如图2 所示。

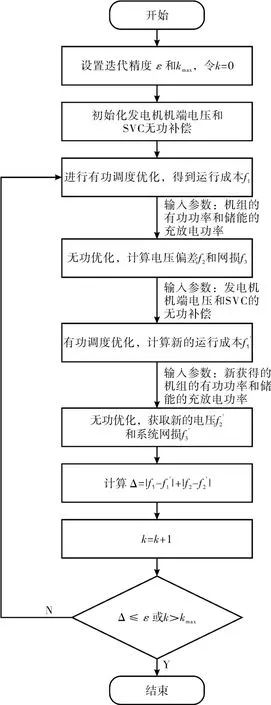
图2 多目标协同经济调度流程

4 算例分析

为了验证本文所提方法的可行性， 以IEEE RTS-24 节点测试系统[23]进行算例分析， 系统结构如图3 所示。 在系统中加入风电机组和储能装置，此系统包含24 个节点， 12 台发电机， 2 个风电场以及2 个储能装置， 在19 号和21 号处接入风电场， 电池储能系统位于节点19 和节点21。 接入系统的风力发电机容量均为200 MW， 设置其功率因数为cosφ = 0.95 ， 储能系统的额定容量为200 MW·h， 充电效率和放电效率分别为0.95 和0.9， 最大充、 放电功率为40 MW， SVC 的无功补偿容量为-15 ～30 Mvar。 将调度运行周期设置为24 h， 每个时段设为1 h， 并通 过MATLAB 调用GAMS 软件对此算例进行分析求解。 设各节点的电压幅值标幺值波动范围为0.95～1.05 p.u.。

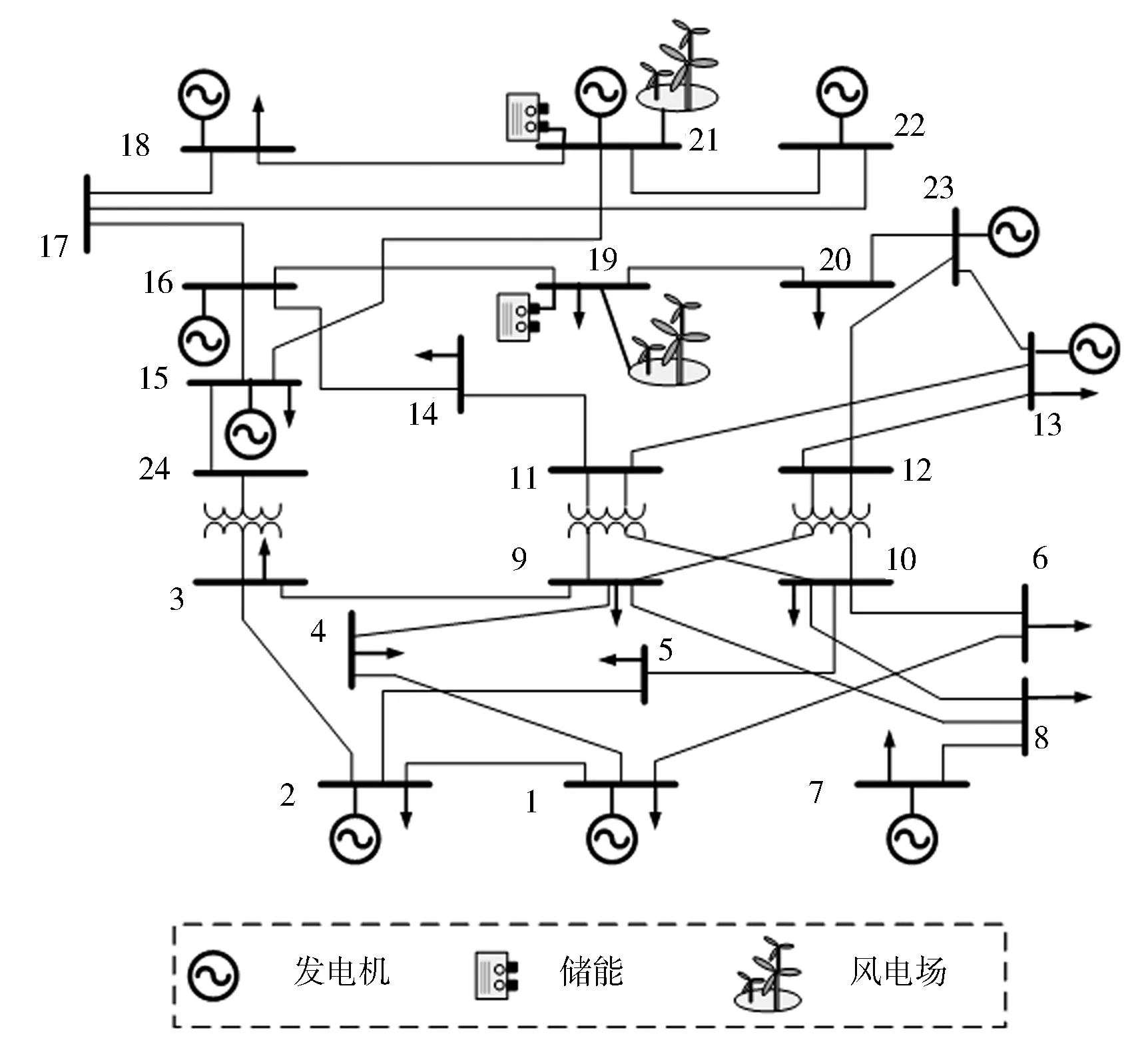
图3 IEEE RTS-24 系统

发电机的技术参数和编号见表1。 该可靠性测试系统峰值负荷为2 850 MW。 风电和负荷的预测曲线如图4 所示。

表1 发电机技术参数

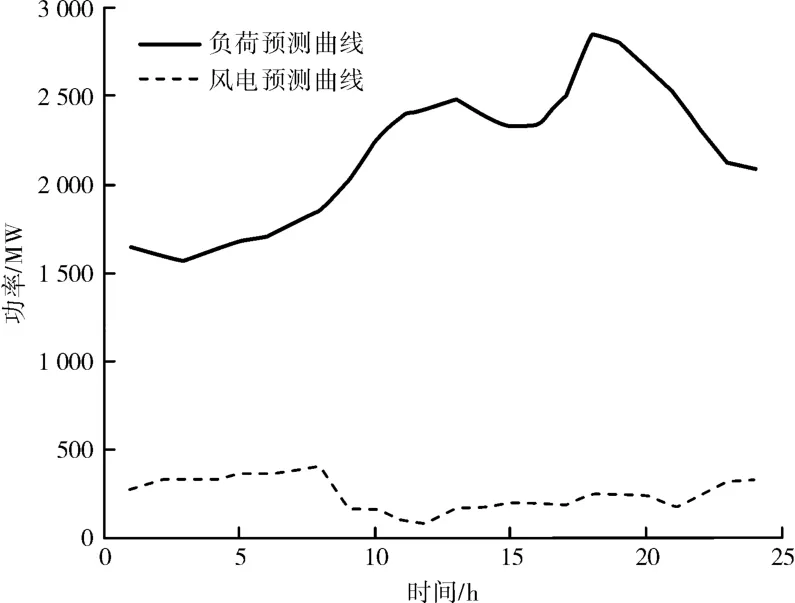
图4 负荷及风电预测出力曲线

设计四种案例: 案例1 在测试系统中只接入风电场， 计算在接入不同功率风电场下的弃风成本；案例2 在系统中接入风电场和储能系统， 利用储能实现减少风电场弃风， 提高系统对风电的消纳能力； 案例3 在系统中接入风电场和SVC， 利用SVC灵活向系统提供无功补偿， 分析其对节点电压的改善作用； 案例4 在含风电场的系统中考虑同时接入SVC 和储能设备， 利用协同算法对有功调度和无功优化模型迭代计算， 获取兼顾电网经济性和安全性的最优解。 将接入系统的风电场功率设置为120 MW到240 MW， 间隔10 MW 逐渐变化， 分别进行优化， 案例1 和案例2 在不同风电接入功率下的弃风成本情况如图5 所示。 从图中可看出， 案例2 中风电功率从120 MW 到160 MW 变化时， 系统的弃风成本都较小， 从170 MW 处开始， 随着风电功率的增加， 其弃风成本逐渐增加； 而案例1 的弃风成本始终比接入储能后的弃风成本大， 这说明储能系统促进了系统消纳风电， 减少了风电弃风。

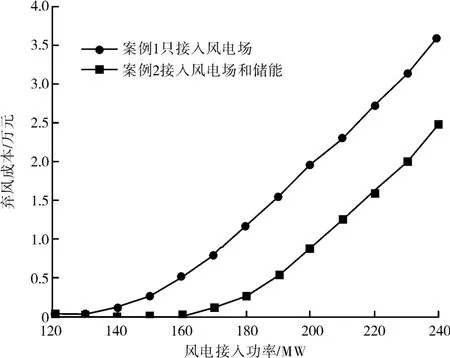
图5 案例1 和案例2 的弃风成本比较

在GAMS 中分别建立有功调度模型和无功优化模型， 经济调度以系统综合运行成本为优化目标， 控制变量为各机组的有功出力和储能的充放电功率， 设发电机的机端电压以及SVC 的初始无功补偿为常数(即初始值)； 在无功优化时， 以系统网损和节点电压偏差最小为目标函数， 其控制变量为发电机的机端电压和SVC 的无功补偿容量。 经过协同迭代后， 储能系统的充放电功率和SOC 变化情况如图6 所示。 由图6 可以看出: 储能系统主要集中在负荷高峰时段(18:00—22:00) 进行放电， 使得储能系统的容量不断减小； 而在负荷低谷时间段(1:00—8:00) 主要进行充电， 储能系统SOC 逐渐增大。

表2 给出了案例4 进行协同优化后的SVC 在各个时段的无功补偿情况。

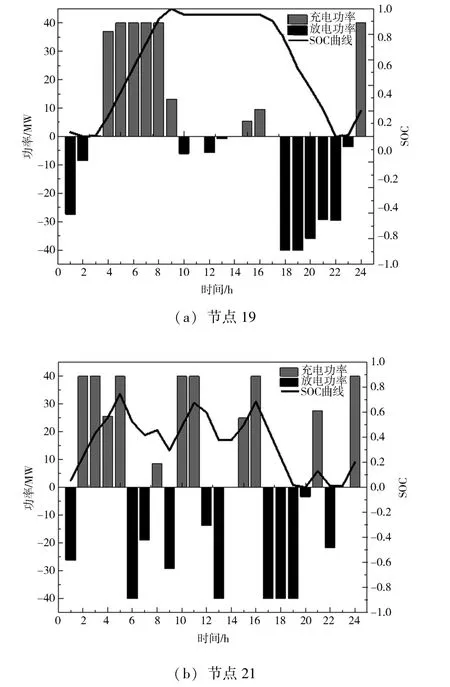
图6 储能系统的充放电功率以及SOC 变化曲线

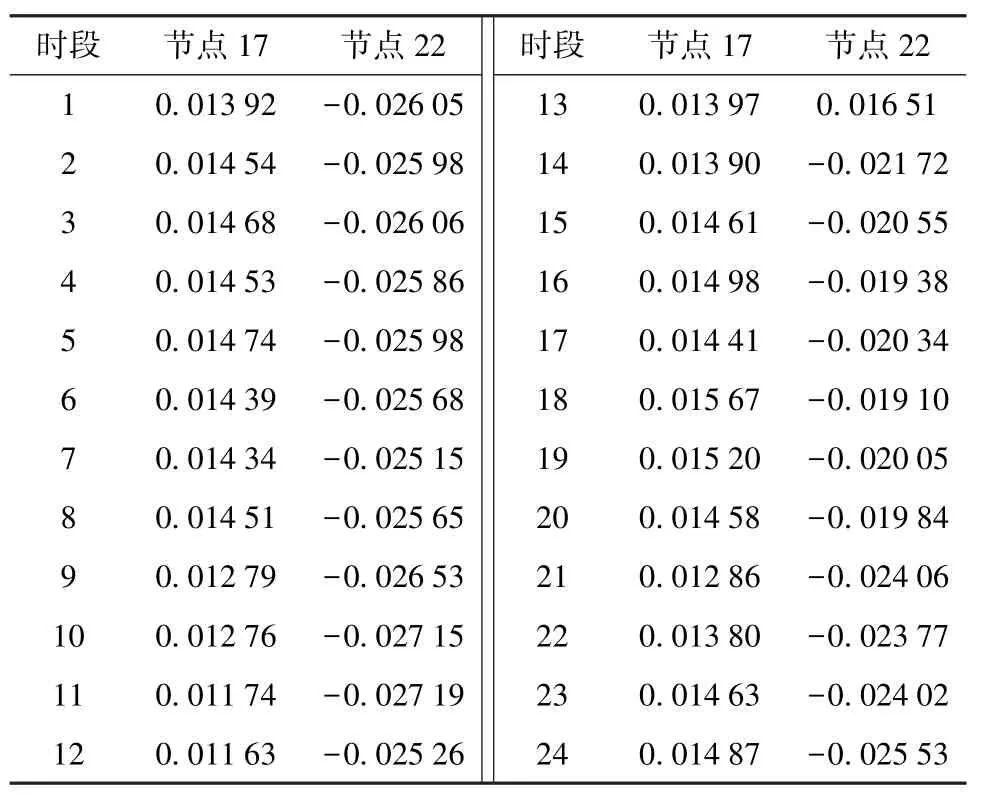
表2 协同迭代后SVC 的无功补偿情况 p.u.

图7 给出了案例2 与案例4 中未加入SVC 与加入SVC (均含储能系统) 优化后的系统节点电压波动情况。 从图中可以看出， 加入SVC 后系统的电压波动幅度进一步减小， 变得更加平稳， 明显提高了电网的电压质量水平。

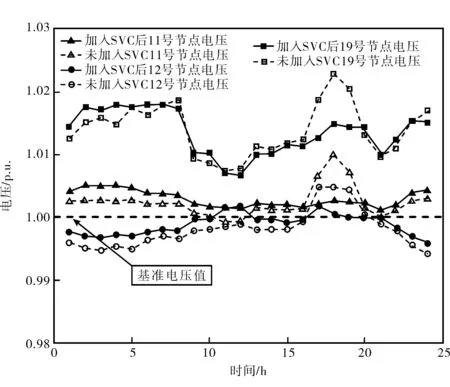
图7 加入与未加入SVC 的节点电压波动对比情况

表3 给出了案例4 与系统中分别只接入储能(案例2) 和只接入SVC (案例3) 时的有功-无功调度优化结果对比。

从表3 中的数据可以看出， 案例4 经过四次协同迭代后， 第三次和第四次系统综合运行成本之差的绝对值为0.001 2， 电压偏差之差的绝对值为0.000 2， 二者之和为0.001 4， 小于所预设的精度值， 故迭代结束。 通过对比发现， 案例3 中系统仅接入SVC 时出现了弃风成本， 这是由于SVC在系统中不能交换有功功率， 无法促进系统消纳风电； 案例2 中系统仅接入储能时， 系统的弃风成本降低至很小， 但系统的网损和电压偏差都比较大。 在案例4 中当同时接入储能和SVC 时， 系统的综合运行成本降低至54.020 3 万元， 其中系统的环境污染费用大大减少， 所以储能装置的接入可以提高系统的经济运行。 在无功调度方面， 通过协同优化后系统的电压偏差和网损为0.119 2 p.u.和56.708 6 MW。 因此将SVC 和储能结合起来运行，有利于保证电网的经济运行和安全运行。

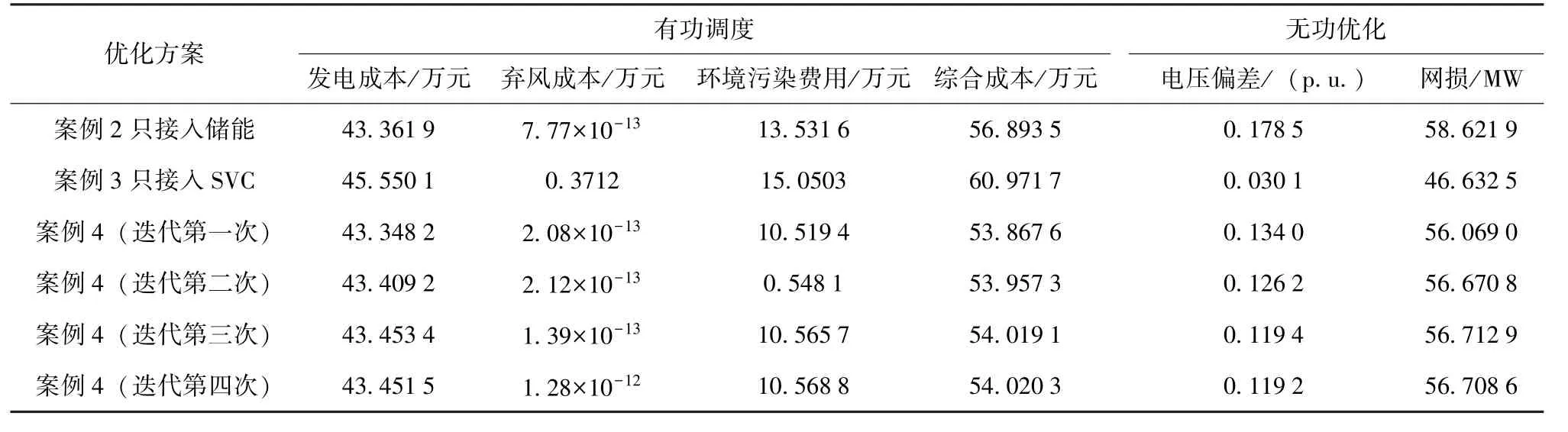
表3 协同优化迭代后的结果对比

图8 给出了选用权重系数法获得的真实Pareto前沿面与基于协同优化算法在文中所述的参数下所得到的Pareto 最优解的情况。 从图中可看出设置权重系数可以得到均匀分布的Pareto 前沿面， 经协同迭代优化所得的Pareto 最优解集很好的落在真实Pareto 前沿上。 在案例3 中系统仅接入SVC 时，系统的电压偏差很小， 故解的位置趋近于水平线；在案例2 中系统仅接入储能设备时， 可提升系统的经济运行， 但不能使得电压波动得到更好的改善。因此， 利用SVC 灵活向系统补偿无功量和储能促进系统消纳风电的特性， 可以获得兼顾电网安全运行与经济运行的最优解。

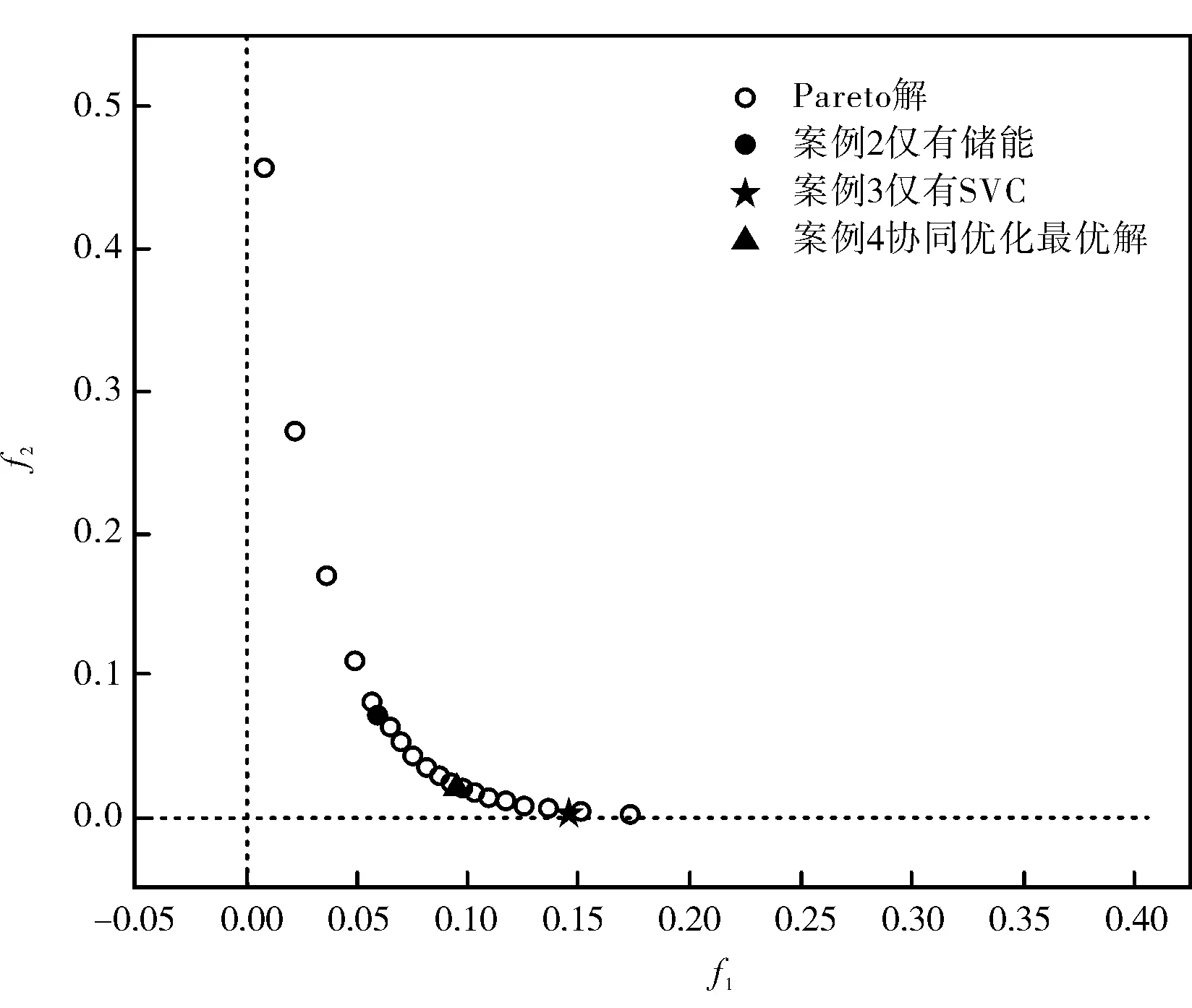
图8 权重系数下的优化结果

5 结论

本文综合考虑储能系统和风电模型， 将SVC装置应用于电力系统经济调度中， 构建了以系统综合运行成本、 系统网损和电压偏差最小的多目标优化调度模型。 在优化过程中， 首先求解有功调度模型， 再进行无功调度的优化， 寻求同时满足电网经济性和安全性的最优解。 通过算例分析， 利用SVC和储能进行协同优化的多目标调度模型， 可同时降低系统成本、 电压偏差和系统网损， 兼顾了提高风电接入后电网的安全性和经济性， 为电网的经济调度优化提供参考依据。