碳税政策下分销网络选址—路径问题的鲁棒优化

周愉峰，刘思峰，苏加福，李 志

(1.重庆工商大学 重庆市发展信息管理工程技术研究中心，重庆 400067;2.南京航空航天大学 管理科学与工程博士后流动站，江苏 南京 210016;3.重庆工商大学 电子商务及供应链系统重庆市重点实验室,重庆 400067)

0 引言

我国是CO2排放大国，正面临着与日俱增的节能减排压力。控制碳排放、促进可持续发展工作已成为政府重要的政策目标。目前，较为通行的碳减排调控措施为碳交易政策和碳税政策。我国较早进行了碳排放权交易政策的研究和实践。2013年，我国首次在7个省市启动碳排放交易试点。2017年12月，我国开始以发电行业为突破口启动全国碳排放交易体系。

碳税也是国际公认的碳减排促进手段。芬兰、丹麦、瑞典、加拿大、日本等国的实践证明了碳税征收对实现碳减排具有积极效用[1]。与基于数量控制的碳交易政策相比，碳税则侧重解决污染排放的价格问题[2]，具有直接有效、覆盖面广、公平性好、可操作性强、GDP损失率小、减排成本低等突出优势。未来，特别是在中短期内，随着环保税体系的逐步设立，以及碳减排和经济可持续发展的需要，碳税将在环境规制的政策层面发挥更加重要的作用[3]。

物流与供应链管理的若干环节都涉及CO2的排放[4]，如生产、运输、库存等流程。近年来，在选址、库存、路径等物流系统优化问题中权衡成本和碳排放量，研究绿色物流与供应链网络的优化问题，已成为研究者们关注的热点。在绿色设施选址问题(Facility location problem, FLP)研究方面，研究者们从以往仅关注经济因素，逐渐转向经济与环境因素并重。Zhang等[5]基于双层规划模型，同时考虑规模经济和碳税对物流网络设计的影响，研究了物流园区的最优选址及其规模确定问题;Elhedhli等[6]考虑CO2排放，研究了供应链网络设计问题。以上文献建立的模型为非凸优化问题，难以直接求解，为此，文献[6]设计了一种拉格朗日松弛算法，将原问题分解为若干单资源有容量约束的FLP进行求解，其计算误差小于1%;Xiao等[7]考虑碳排放因素,研究了四级逆向物流网络设计中的选址—分配问题，构建了混合整数线性规划模型，并利用Lingo软件求解模型;Diabat等[8]研究了考虑碳排放交易价格和采购成本的多级多商品FLP，并分析了不同碳交易价格对供应链成本和配置的影响;杨珺等[9]研究了4种不同碳排放政策下的多容量等级设施选址—分配问题，建立了相应的混合整数线性规划模型，并运用CPLEX软件对模型进行数值计算。

在绿色车辆路径问题(Green Vehicle Routing Problem, GVRP)研究方面，现有研究通常通过油耗模型或者计算交通排放和能源消耗的方法来刻画VRP建模时应考虑的环境因素。Kara等[10]最早扩展了有容量限制的车辆路径问题(Capacitated Vehicle Routing Problem, CVRP),研究了能耗最小化的CVRP，并将其描述为整数线性规划问题，采用了CPLEX求解;Andelmin等[11]将GVRP模型转化为集合划分问题，提出一种精确算法;Raeesi等[12]假设碳排放量与时间和负载相关，以车辆租赁成本最小、燃料消耗总量最小以及路径时间最短为目标函数，研究了带时间窗的多目标污染—路径问题(Pollution-Routing Problem, PRP);Ashtineh等[13]将距离、负荷、速度和传动比作为影响车辆排放的主要因素，通过建立混合整数规划模型研究了具有可替代燃料的VRP(vehicle routing problem)，其研究评估了VRP中替代燃料的经济性和环境绩效;Demir等[14]以耗油量最少和行驶时间最短为目标，研究了双目标PRP模型，并设计了相应的自适应领域搜索算法;Macrina等[15]将速度、加速度、减速、负荷等因素纳入综合能耗模型，研究了由电动车和传统内燃机车组成的混合车队绿色VRP模型，并设计了一种嵌入式大领域搜索启发式算法;Franceschetti等[16]考虑交通拥堵会显著限制车辆速度、增加碳排放，研究了时变速度的PRP;Fukasawa等[17]研究了求解PRP的分离凸规划方法;Dabia等[18]提出了求解PRP的分支定界算法。此外，文献[19-21]也从不同角度研究了GVRP。

选址—路径问题(Location-Routing Problem, LRP)是FLP与VRP的集成。FLP与VRP之间存在相互影响相互制约的关系，经典的LRP研究文献证明了通过两者的集成优化可以降低系统成本，促进决策的科学化[22]。目前，有关绿色LRP的研究较少，Govindan等[23]最早研究绿色LRP，以总成本和环境影响最小为目标，建立了带时间窗的双目标两级LRP模型，并设计了一种粒子群优化与自适应领域搜索相结合的混合多目标优化算法;Koç等[24]在系统成本中考虑燃料消耗和二氧化碳排放，研究了城市物流中的LRP，提出一种新的自适应大邻域搜索启发式算法;Toro等[25]提出一种计算车辆行驶路线温室气体排放的新模型，研究了考虑环境影响的有容量约束LRP,其研究表明，使用更多的车辆可以带来更大的燃油经济性从而减少排放，且在短路线上启用更多的车辆并优先考虑高需求的客户，也可以减少排放;Dukkanci等[26]在经典LRP与PRP的基础上研究了有容量限制的绿色LRP;唐金环等[27]研究了顾客有限“碳行为”偏好对选址—路径—库存联合优化的影响。

综上所述，已有不少文献对供应链运作优化中的碳排放问题进行了研究，取得了许多研究进展，但仍有一些问题亟待解决：

(1)在碳税日益成为政界和学界关注热点的背景下，碳税征收对供应链上企业的分销网络选址—路径决策具有哪些影响？政府应该如何制定碳税？在碳税影响下，企业如何决策更有利？现有研究对上述问题还缺少解答。

(2)以往对绿色LRP的研究均基于确定性优化或随机优化，随机优化比确定性优化更加符合实际情况，但也存在一些局限：①很难确定有代表性的情景及其概率，或者不确定参数的概率分布函数;②随机优化中最小化期望成本的决策目标难以体现决策者的风险偏好;③随机优化模型大多为非线性混合整数规划，需用启发式或者亚启发式算法求解，难以得到全局最优解。而鲁棒优化在一定程度上弥补了随机优化模型的局限。

现实生活中，分销网络运作的一些参数具有不确定性。例如，单位运费受交通拥堵、油价波动、人工成本变化等因素的影响，具有明显的波动性。因此，本文在传统供应链分销网络LRP基础上，引入box不确定集合与两类不确定水平参数来描述单位运费的不确定性，建立了考虑碳税政策与碳排放的多容量等级LRP鲁棒优化模型。基于强对偶理论，将非线性的混合整数规划模型转化为线性鲁棒等价模型，并采用GUROBI软件计算模型的最优解。最后，通过数值计算与关键参数的敏感性分析，得出一些管理启示，为政府与企业提供决策参考。

1 模型研究

1.1 问题描述

本文以一个三级分销网络为研究对象，该网络由若干工厂、配送中心和需求点组成，其中工厂的地点和规模是确定的，候选配送中心有容量限制且有多个容量等级可选。在多容量等级FLP中，除了设施位置的决策变量之外，容量等级也属于决策变量[9]。通过设施位置、数量和容量的整体优化，可以减少设施资源与客户需求匹配之间的不均衡问题。需求点的位置和需求已知，且其需求只由一辆车满足。车辆也有容量限制，每条巡回路径上只有一辆车，每辆车完成配送任务后需返回配送中心。分销网络中的碳排放来自配送中心选址碳排放，运营碳排放以及工厂—配送中心—需求点的运输/配送碳排放。碳税政策下，政府对企业排放的CO2进行征税。此时，企业实际的总成本需增加一项碳税成本。

需要作出以下决策：①确定开放配送中心的位置、数量和容量等级;②确定运输量的分配，包括工厂到配送中心的运输量、配送中心到需求点的运输量;③确定配送中心到需求点的配送路径。

1.2 参数与变量

(1)集合

I为配送中心集合；

M为工厂集合；

J为需求点集合；

V为运输车辆集合；

K为容量等级集合。

(2)参数

fik为在候选配送中心i建设容量等级为k的配送中心的建设成本分摊，∀i∈I,k∈K；

hj为需求点j的需求量，∀j∈J；

γik为在备选点i建设等级为k的配送中心单位运营成本，∀i∈I,k∈K；

cik为在备选点i建设等级为k的配送中心的最大容量，∀i∈I,k∈K；

dmi为工厂m到配送中心i的运输距离，∀m∈M,i∈I；

bmi为从工厂m到配送中心i的单位产品单位距离的运费，∀m∈M,i∈I；

blj为从节点l到需求点j的单位产品单位距离的运费，∀l∈(I∪J)，j∈J；

c为单位距离的车辆空驶成本；

c0为单位车辆的固定出车成本；

dlj为从节点l到节点j的运输距离，∀l∈(I∪J)，j∈J；

capv为车辆v的最大运载能力，∀v∈V；

H为一个大数；

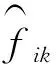
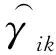
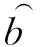
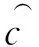
∂为碳税率。

决策变量：

qmi为从工厂m到配送中心i运输的产品数量，∀m∈M,i∈I；

qlj为从节点l到节点j运输的产品数量，∀l∈(I∪J)，j∈J；

xljv为若车辆v从节点l开出后开向节点j为1，否则为0，∀l∈(I∪J)，j∈J，v∈V；

Xik为在i点建立容量等级为k的配送中心为1，否则为0，∀i∈I,k∈K。

1.3 单位运费的不确定性刻画

现实生活中，受拥堵、油价波动等因素的影响，单位运费bmi与blj具有明显的不确定性。考虑单位运费的不确定性，引入box不确定集来刻画单位运费bmi与blj[28]。

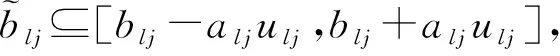
1.4 数学模型

运用鲁棒优化方法，建立碳税政策下分销网络优化设计中的LRP鲁棒优化模型[28]。由于不确定性仅存在于目标函数中，得到box不确定集LRP鲁棒优化模型Ⅰ。

模型Ⅰ:

(1)

s.t.

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

xijv=0,∀i∈I,j∈I,v∈V;

(14)

(15)

Xik∈(0,1),∀i∈I,k∈K;

(16)

xllv∈(0,1),∀j∈J,l∈(I∪J),v∈V。

(17)

目标函数是指系统总成本最小，其中：第1项为设施建设成本，第2项为配送中心的运营成本，第3项为车辆空驶成本，第4项为固定出车成本，第5项为配送中心到需求点的运输成本及其不确定波动成本，第6项为工厂到配送中心的运输成本及其不确定波动成本，第7项为碳税成本。约束(2)为车辆的容量约束;约束(3)表示保证任意需求点有且只有一辆车为其服务;约束(4)表示每辆车最多服务于一个配送中心;约束(5)表示车辆不能停留于某一个节点上;约束(6)表示运入配送中心的产品数量不小于从配送中心运出的数量;约束(7)保证了所有需求点的需求都能得到满足;约束(8)表示每个配送中心最多有一个容量等级;约束(9)与约束(10)为配送中心运入与运出两个方向的容量限制;约束(11)～约束(13)表示执行任务的配送中心必须开放;约束(14)表示车辆不能从一个配送中心驶向另一个配送中心，减少解空间的搜索规模;约束(15)表示每条路径开始并终止于同一个配送中心;约束(16)和约束(17)为0-1变量约束。

当Γ(Γ1,Γ2)=0时，box不确定集鲁棒模型Ⅰ等价于其名义模型。模型Ⅰ的目标式(1)含有两个内层最大化问题，可通过强对偶理论将其转换为更易于求解的鲁棒等价模型。以第一个内层最大化问题(18)为例：

(18)

考虑内层最大化的线性规划问题：

(19)

s.t.

(20)

0≤ulj≤1,∀l∈I+J,j∈J。

(21)

根据强对偶原理，问题等价为：

minρlj+Γ1θ1。

(22)

s.t.

ρlj+θ1≥aljdljqlj,∀l∈I+J,j∈J;

(23)

ρlj,θ1≥0,∀l∈I+J,j∈J。

(24)

其中ρlj与θ1为对偶变量。

综上所述，将式(18)和式(22)代入式(1)，可将第一个内层最大化问题予以转化，得到新的目标函数：

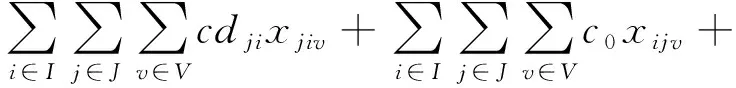
(25)

采用同样的方法处理另外一个内层最大化问题，得到两类不确定运费参数下LRP鲁棒优化问题的线性等价模型Ⅱ。该模型为线性混合整数规划模型，可用GUROBI、CPLEX等运筹学软件进行求解。

模型Ⅱ：

(26)

s.t.

τmi+θ2≥amidmiqmi,∀m∈M,i∈I;

(27)

τmi,θ2≥0,∀m∈M,i∈I。

(28)

同时，约束(2)～约束(17)，约束(23)，约束(24)成立。

2 数值计算与分析

2.1 参数取值

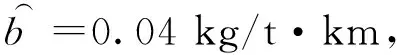
表1 不同容量等级配送中心相关参数

2.2 计算结果

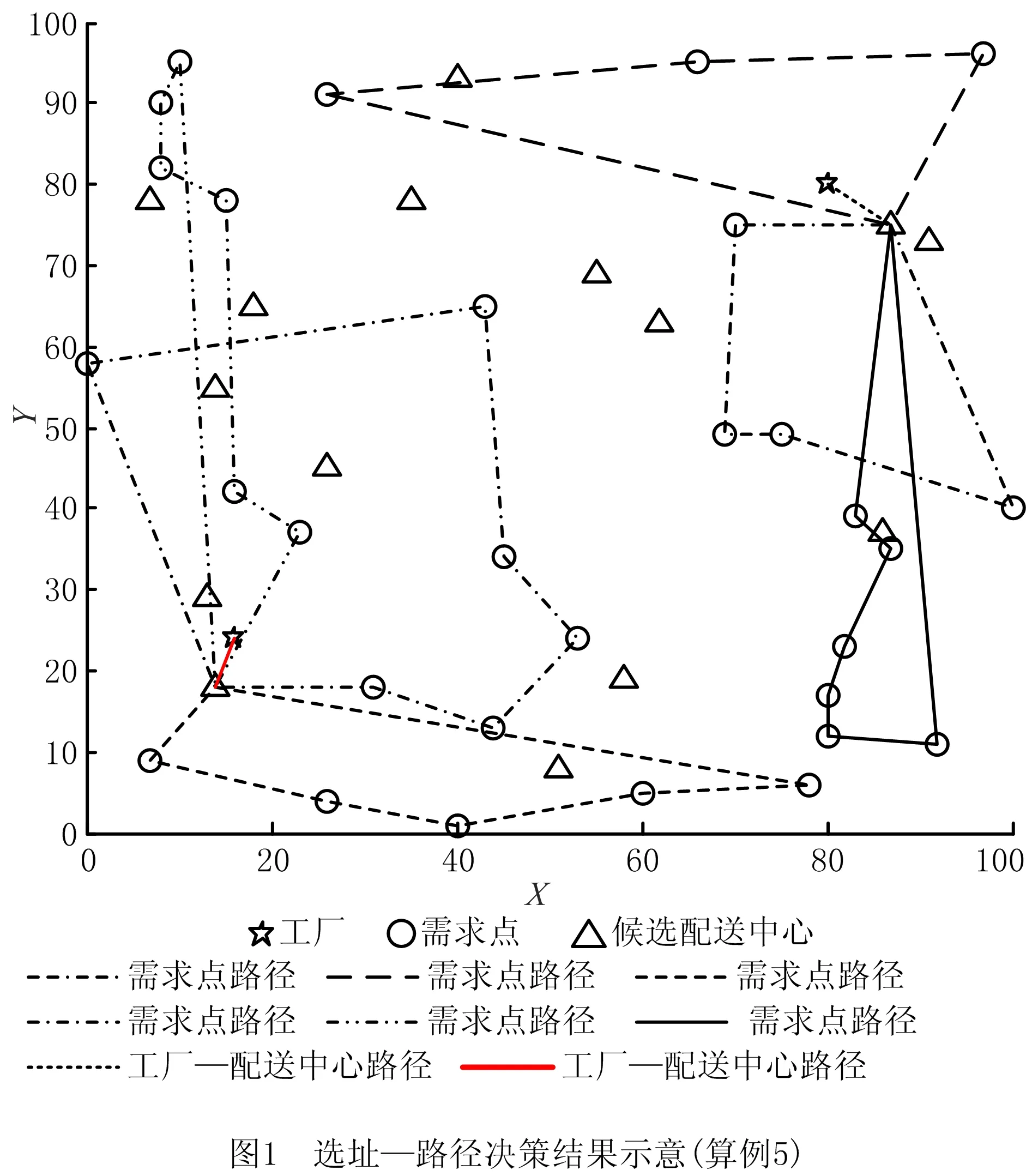
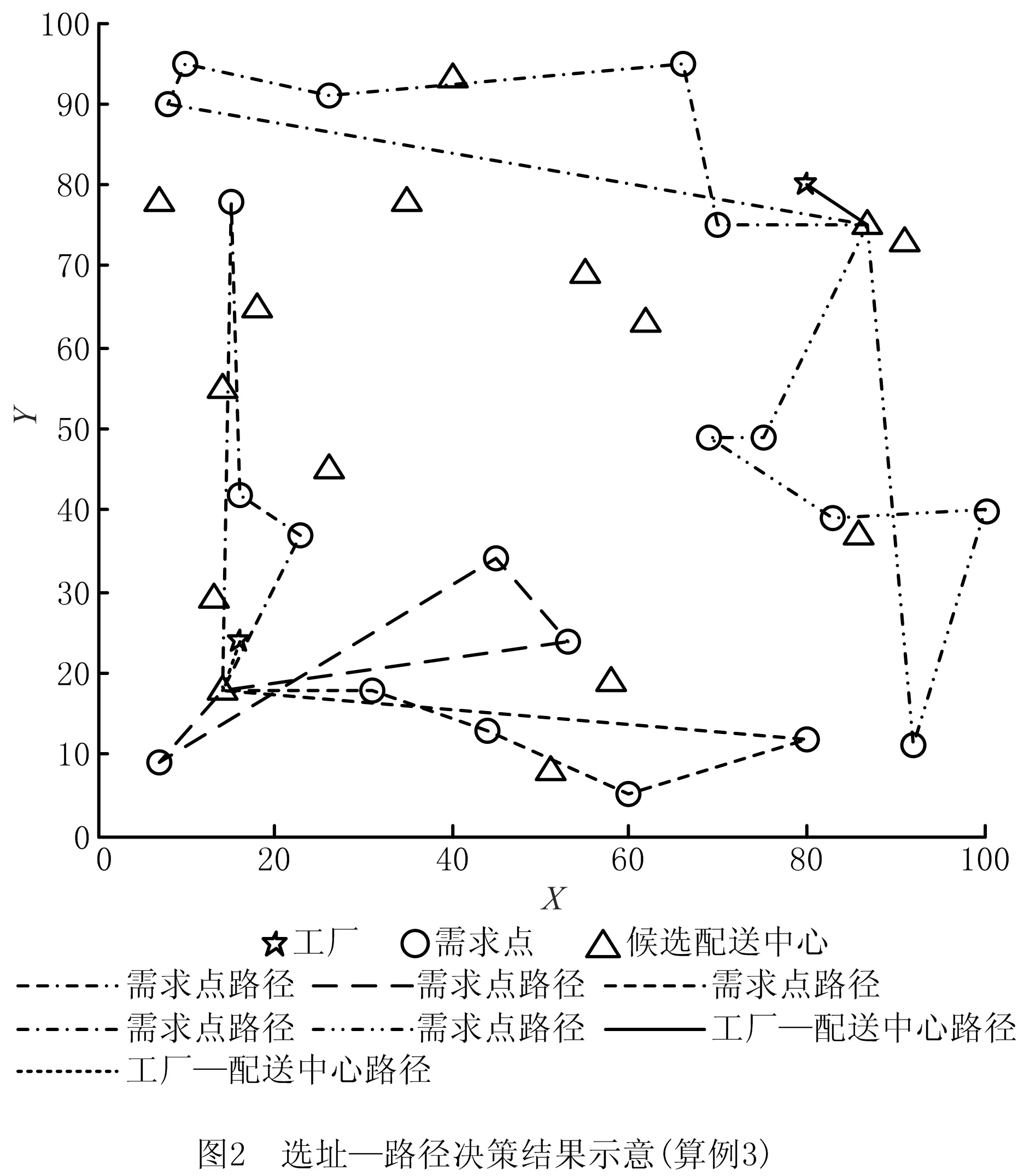
实验发现，影响目标值的主要网络结构参数是需求点数量。因此，根据需求点数量，设置5个不同规模的算例。采用运筹学计算软件GUROBI 8.0.1计算模型，得到5个算例的计算结果如表2所示，两个算例的选址—路径决策结果示意图如图1和图2所示。

表2 选址—路径决策结果

2.3 碳税政策对LRP决策的影响

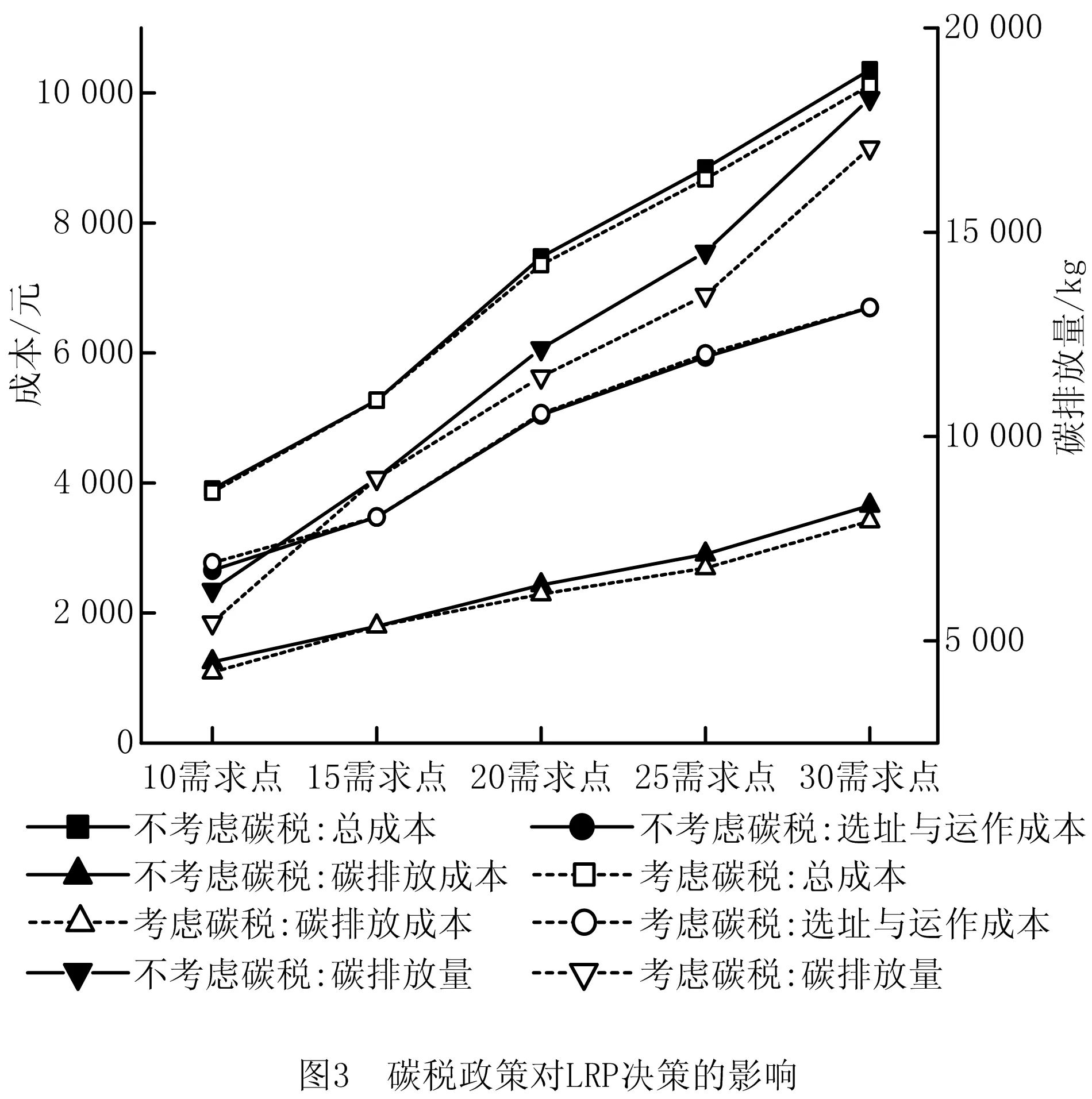
为了分析碳税政策对企业决策的影响，分别计算不考虑碳税政策的LRP(将模型Ⅰ的目标函数去掉运费波动成本与碳税成本即可)与考虑碳税政策但不考虑运费波动的LRP(将模型Ⅰ的目标函数去掉运费波动成本)，结果如表3与图3所示。本文将碳税成本定义为碳排放成本，碳排放成本以外的其他成本定义为选址与运作成本。需要说明的是：不考虑碳税政策的LRP计算结果本身不含碳排放量与碳排放成本。通过计算模型的最优解，再将其代入考虑碳税政策但不考虑运费波动的LRP得到该决策方案在碳税政策下的碳排放量、碳排放成本与实际总成本。5个算例的计算结果表明，多数情况下(4个算例)碳税政策可以有效降低企业的碳排放量，碳减排比例分别为12.77%、5.72%、7.25%与6.59%。因此，碳税政策具有减排效应。对政府而言，碳税是一种较为有效的碳减排调控措施。由表3和图3可知，对企业而言，虽然不考虑碳税政策的决策方案，其选址与运作成本更低，但由于忽略了碳税政策的影响，导致碳排放成本和总成本上升，总成本上升比例分别为1.18%、1.57%、1.88%与2.30%。因此，碳税政策具有明显的减排效应。对企业而言，在选址—路径运作决策中，考虑碳税政策的影响，可以降低系统总成本。

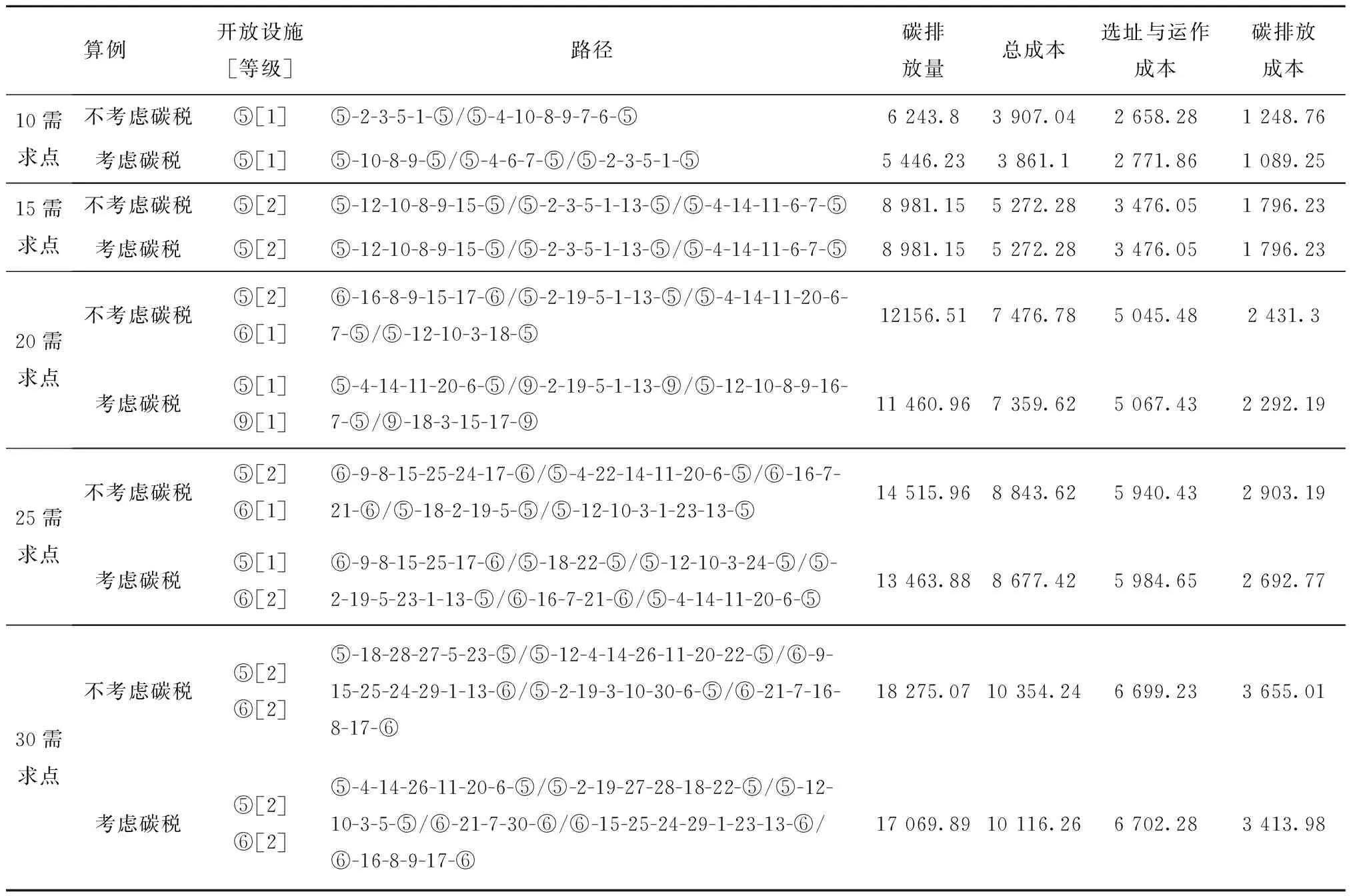
表3 不考虑碳税与考虑碳税政策的LRP决策结果比较

2.4 碳税率的敏感性分析

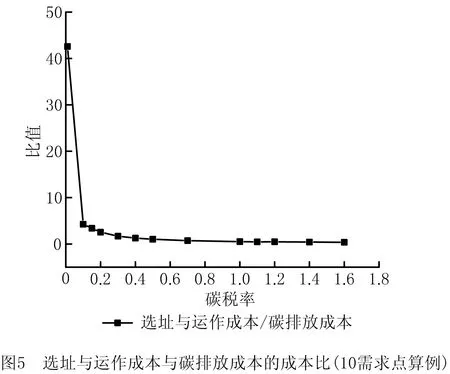
接下来分析碳税率变动对决策结果的影响。为了剔除运费变动对结果的影响，依然采用考虑碳税政策但不考虑运费波动的LRP模型对碳税率∂进行敏感性分析。以10需求点算例为例，计算结果如表4所示。随着碳税率的持续增加，系统总成本与碳排放成本显著增加，而选址与运作成本的增加不明显(如图4)。如图5所示，表现为选址与运作成本/碳排放成本的比值不断下降。显然，征收碳税将导致企业系统总成本显著上升，这是因为碳税率的上升会引起碳排放成本的快速增加，进而导致总成本上升，如图6中碳排放成本与总成本的快速增加;碳税政策也会引起选址与运作成本的上升，但上升幅度较小，且呈“阶梯式”上升趋势，如图6中选址与运作成本的阶梯式小幅度上升。

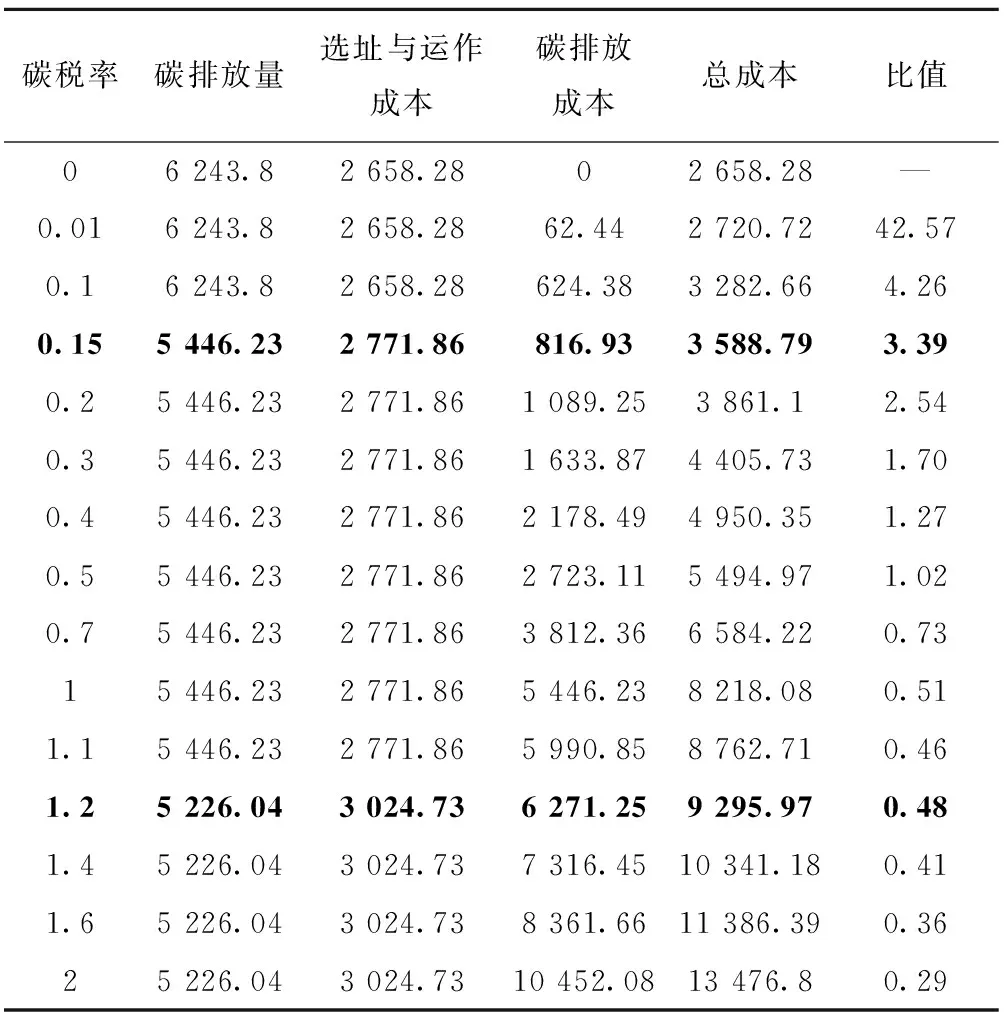
表4 碳税率∂的敏感性分析(10需求点算例)

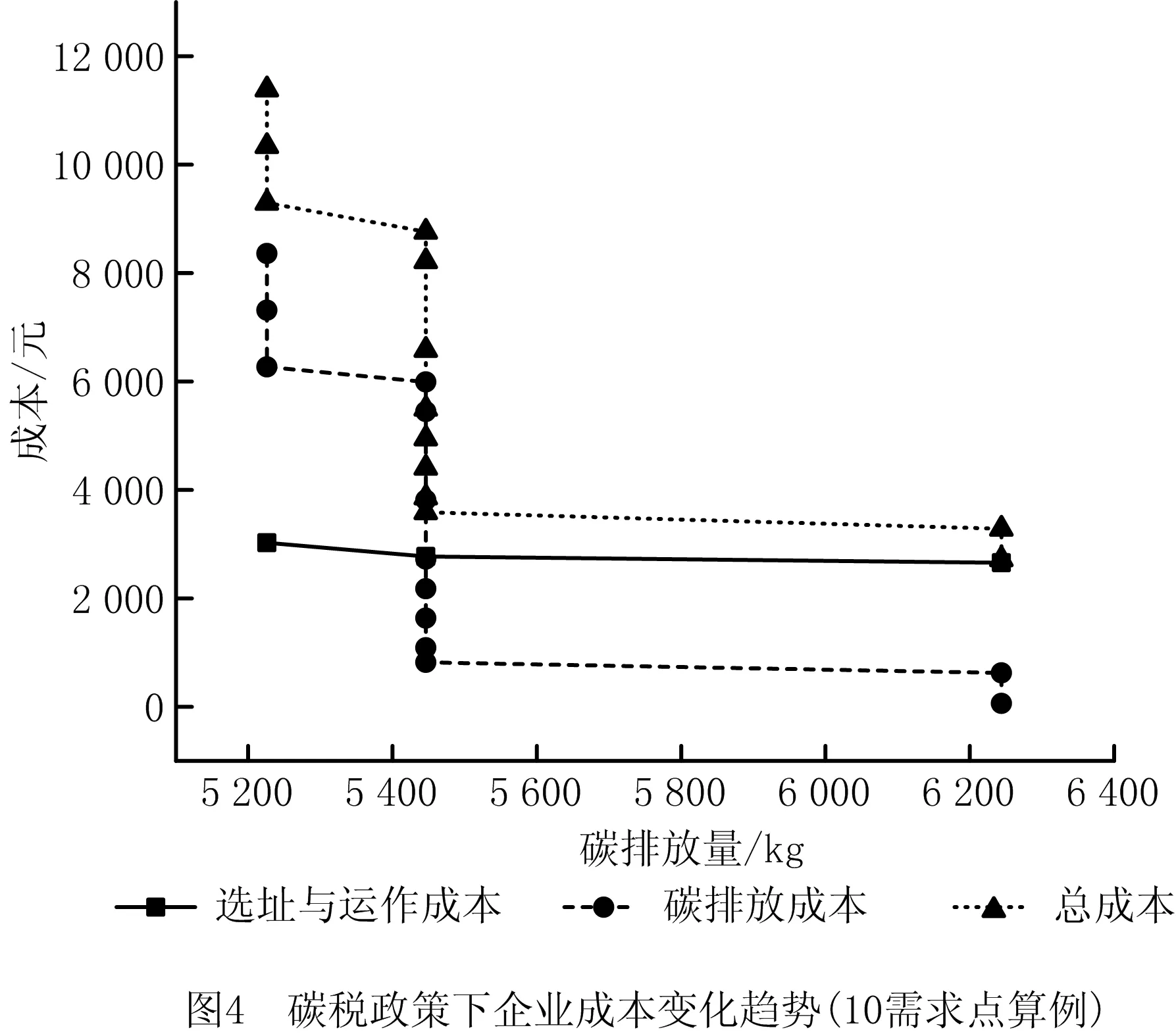
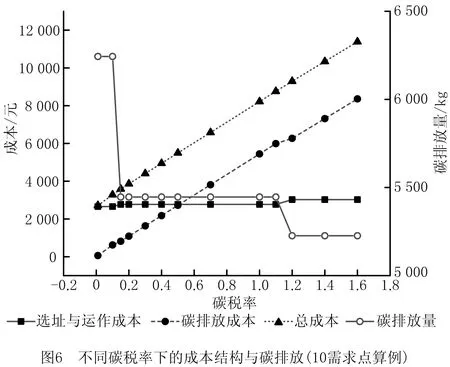
从表4、图4和图6可以看出，较高的碳税率可以约束企业降低碳排放。但随着碳税率的增大，碳排放量呈现出“阶梯式”下降的趋势。在碳税率很低时，即使碳排放量很高，但因为碳排放成本低，企业倾向于保持原有的最优决策。例如，碳税率由0增加到1%的时候，碳排放成本与总成本仅增加62.44，此时企业保持原有的最优决策，总成本还是最低的。而当碳税率增加到一定阈值时，碳排放成本显著增加，此时企业有必要调整最优决策，降低碳排放量与碳税成本，以实现系统成本的最小化。例如，当碳税率由10%增加到15%的时候，通过调整最优决策，选址与运作成本仅增加4.10%，碳排放量下降12.77%。当碳税率高于15%时，企业的最优决策在一定碳税率范围内保持不变，直到碳税率增加到约120%的时候才再次发生变化。在此区间内，即使碳税率增加，企业只会增加生产成本，不会减少碳排放量。该现象说明：虽然总体上碳税政策具有碳减排效应，但减排效应的效果受到市场中企业生产规模的影响。

因此，在宏观调控的视角上，政府应该根据市场规模与结构，设置合理的碳税率，在企业成本增加不多的情况下，促进企业改变最优决策、减少碳排放，以实现最优的减排效果。而在微观运作视角上，对企业而言，需找准当前状态下的碳税率阈值，在不超阈值的情况下，可以维持原有的最优决策，甚至适量增排，以减少选址与运作成本和系统总成本；反之，则应该追求低排放与低碳税支出，以降低总成本。

2.5 鲁棒控制参数的敏感性分析

最后对鲁棒控制参数进行敏感性分析。改变单位运费的不确定水平参数Γ1、Γ2，以及单位运费的扰动比例εl、εm，求解线性化的鲁棒优化模型V，得到不同鲁棒控制参数组合下的最优决策结果，如表5所示。表5中，黑色加粗部分表示最优的选址—库存决策结果发生了变化。结果表明，分销网络规模越大，鲁棒控制参数的取值对最优决策的影响越明显；且不确定水平参数与扰动比例越大，最优决策结果的变化越明显。例如，在10需求点算例中，不确定水平参数Γ=1，扰动比例ε分别取0.05和3；Γ分别取3和10，ε分别取0.05和3，最优决策结果不变；当鲁棒控制参数组合为Γ=1，ε=5时,才发生最优解的变化。在15需求点算例中，不断扩大Γ与ε的取值，直到Γ=10，ε=2时最优解才发生变化;而在20需求点算例与25需求点算例中，Γ与ε的较小波动也能引起最优决策结果的变化。此外，扰动比例的增加会引起系统总成本的增加。

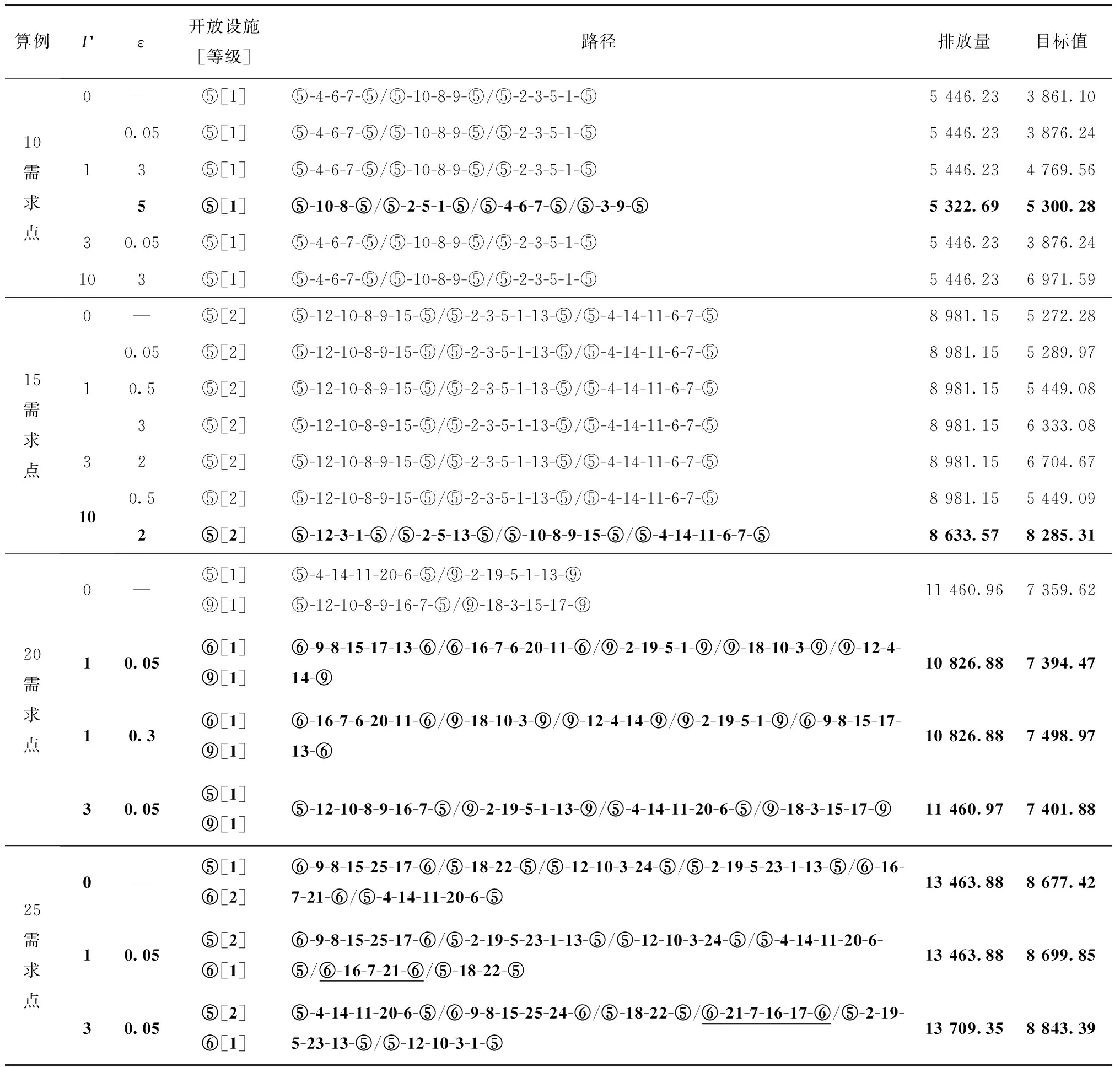
表5 不同鲁棒控制参数组合下的决策结果

因此，单位运费的不确定波动等因素会对企业的最优决策产生影响，且分销网络规模越大，参数的不确定性对决策结果的影响越明显。由于配送中心的多容量选址问题属于战略性决策问题，分销网络一旦建立，短期内难以改变。因此，企业在进行选址—路径集成决策时，需充分考虑单位运费等参数的不确定性，寻求更加稳健的决策方案。

2.6 路径解特征

分析表4和表5中的路径解特征及其数量可以发现：启用更多的车辆数可以减少排放；在短路线上启用更多的车辆，并优先考虑高需求的客户，也可以减少排放，如表3中25需求点算例，30需求点算例以及表5中10需求点算例的黑色加粗部分，均通过增加一台车辆缩短了平均路线长度，降低了碳排放量；再如表5中25需求点算例的两条下划线路径，通过先配送高需求客户点21后配送低需求客户点16降低了碳排放量。该结论与文献[24]结论相同。这是因为启用更多的车辆、减少路径长度且优先配送高需求客户，可以降低车辆行驶中的平均负载，在一定范围内可以减少碳排放。但显然，启用更多的车辆将增加运作成本。

因此，企业需要根据实际情况启用车辆以权衡运作成本与碳税成本：在碳税率较高或者即将超过当前碳税率阈值时，可考虑开启更多的车辆，并且优先配送高需求量客户点，以降低碳排放成本和总成本;反之，则应该启用更少的车辆，以更多地降低选址与运作成本。

3 结束语

本文在传统三级分销网络优化设计模型的基础上，纳入配送中心选址碳排放、运营碳排放，以及工厂—配送中心—需求点的运输/配送碳排放等分销网络中的碳排放因素，同时进一步引入box不确定集合描述单位运费的不确定性，建立了考虑碳税政策与碳排放的多容量等级分销网络LRP鲁棒优化模型。采用混合整数非线性规划构建了相应的数学模型。由于混合整数非线性规划模型的精确求解难度很大，本文采用强对偶理论将非线性模型转化为线性化的鲁棒等价模型，并采用GUROBI求解器进行了计算和数值分析，得出了若干结论与管理启示。实际工作中，决策者可以根据自己的偏好与风险厌恶程度选择适当的鲁棒控制参数值，确定分销网络的选址—路径决策方案。

未来，可以在LRP决策中集成库存决策，研究选址—库存—路径问题;也可考虑更多不确定参数，如需求、供应量等，研究多类不确定参数下的LRP鲁棒优化模型。