实例检索中基于关联函数和D-HS索引的改进与融合

赵燕伟，徐 晨，任设东，桂方志，朱 芬

(1.浙江工业大学 机械工程学院，浙江 杭州 310014；2.浙江工业大学 计算机科学与技术学院，浙江 杭州 310023)

0 引言

实现国家现代化的基础在于发展实体经济，制造业是其支柱和核心[1]。随着德国工业4.0及中国制造2025等战略的提出，智能制造已成为全球制造业发展的共同趋势与目标[2]，但在经济全球化的趋势下，制造业市场的竞争日趋激烈，用户对产品的个性化需求也越来越高[3]。在此背景下，产品设计周期变的越来越短，这给企业带来了繁重的产品开发任务，设计人员面临的压力与日俱增[4-5]。产品设计者在分析3种产品设计类型(变型设计、适应性设计和创新设计)时发现，变型设计和适应性设计占比较大，这意味着产品设计经常以原有设计为基础，适当进行修改。因此，根据用户个性化需求，在产品实例库中高效、准确地检索来获得相似实例是设计人员借助计算机辅助设计系统对现有实例进行修改和重用的关键[6-7]。

实例推理(Case-based Reasoning, CBR)[8-9]是指利用过去解决同类问题的方案和经验来获得当前问题解决办法的一项在人工智能领域兴起的技术。实例检索是实例推理系统的中心环节，其检索速度及精度关系着整个系统的质量[10]。因此，众多专家学者对该环节展开了深入的研究，文献[11-12]针对低碳设计中的实例检索问题，提出一种基于多维关联函数的多属性相似实例检索方法，并将其应用于螺杆空压机的低碳属性需求检索中；朱芳来等[13]将基于混合属性距离的相似性度量方法应用于实例检索中，以阀门概念设计中实例检索为例，验证了该应用对提高CBR系统的有效性和可靠性的帮助；蒋占四等[14]针对最近邻实例检索中实例属性相似度和权重的计算问题,提出了区间值属性相似度的计算模型和基于相似度离差信息的客观赋权方法；殷亮等[15]基于子空间法的实例分类，提出一种多级实例检索方法，将检索过程分为实例模板的检索和模板内的实例检索，并采用最邻近法计算实例相似度。

综合分析上述文献不难得出，如何衡量实例间的距离是实例检索的核心问题。关联函数、混合属性距、最近邻法及其改进研究等相继被提出，且在索引精度提升的基础上成效斐然。但实例检索是索引精度和索引速度这一对基本矛盾的有机结合，日趋复杂的计算方法在提高精度的同时带来了庞大的计算量，导致索引速度下降。此外，索引速度不仅受索引精度的制约，还受实例库内实例数目的影响，在实例库的构建过程中，为使实例知识尽可能丰富，设计者往往会不断地更新实例库。因此，实例检索中存在一部分影响索引速度且无益于索引精度的冗余计算，文献[16]称此为检索效用问题。

本文针对索引速度与索引精度间的矛盾问题，结合模糊数与关联函数，提出模糊关联函数的概念，并推导出相应计算公式，同时摒弃面对多属性产品时计算量庞大的全维关联函数计算方法，结合层次分析法建立单维关联函数组合相似性度量模型；此外，基于Sigmoid函数对D-HS索引进行改进，并融合改进后的D-HS索引和关联函数度量模型，避免了实例检索中的部分冗余计算，有效解决了检索效用问题。

1 相关知识

1.1 关联函数

关联函数[17-18]类比于模糊集理论中的隶属度函数，能够定量刻画事物属于某区间或者拥有某性质的程度，相较于传统欧式几何距方法、K最近邻(K-Nearest Neighbor, KNN)分类检索方法，将关联函数应用于实例检索能更为准确地反映产品间的相似程度[12]。关联函数k(x)的表达式如式(1)所示：

(1)

式中ρ(x,x0,X)和ρ(x,x0,X0)表示侧距，

(2)

式中：x,x0分别表示空间上某点及最优点;X表示空间中的范围约束；X1,X2分别表示点x与x0的连线与区间X边界的交点，其中X1为离x0较近的点；Ext(x0X1)表示沿直线x0X1并以X1为起点的射线，Ext(x0X2)同理；x=x0表示点x和最优点x0重合；-max{|x0M|}中M表示区间X各顶点，-max{|x0M|}意为取最优点x0与区间各顶点距离最大值的负数。侧距ρ(x,x0,X0)与侧距ρ(x,x0,X)仅在区间约束上存在差异，计算方法相同(即将X1,X2替换为x1,x2)，故此处略去其具体公式。D(x,X0,X)表示位值,

D(x,X0,X)=ρ(x,x0,X)-ρ(x,x0,X0)。

(3)

由式(3)可知，位值D(x,X0,X)等于以X为区间的侧距ρ(x,x0,X)与以X0为区间的侧距ρ(x,x0,X0)的差值。

1.2 D-HS索引

最高离散化相似度(Discretized-Highest Similarity, D-HS)[19-20]索引方法的核心思想是对实例库中实例的各属性值进行离散化处理，划定每个属性对应的区间长度及数目，判断实例库实例与目标实例是否落入相同区间并计算属性匹配度(计算方法如式(4))，提取出与目标实例存在共同区间的相似实例组成初步索引集SP，再对SP内元素按照属性匹配度的大小进行降序排序，最后剔除其中属性匹配度较低的实例，形成最终索引集SE。

(4)

式中:SA(ci,T)表示实例库实例ci与目标实例T的属性匹配度；vj(ci)和vj(T)分别表示实例库实例ci的第j个属性对应的属性值和目标实例T的第j个属性对应的属性值；当vj(ci)和vj(T)落入同一区间时Match(vj(ci),vj(T))取1，否则取0；M表示实例属性总数。

2 基于关联函数的相似性度量

由1.1节中关联函数和侧距的求解公式可知，直线xx0与约束X、X0间交点(即点x1、x2、X1、X2)的获取是问题的核心，也是计算工作量的关键部分，而交点的获取本质上是对线性方程组的求解，由参考文献[21]可知采用高斯消元法求解线性方程组的时间复杂度为O(n3)，其中n指代方程的个数(高斯消元法求解线性方程组可以分为消去过程与回代过程两个步骤，其中消去过程的计算工作量为[n(n+1)(2n+1)/6]-1，回代过程的计算工作量为n(n+1)/2，总计算工作量为n3+n2+2n/3-1，时间复杂度仅以最高次幂为代表，故记为O(n3))，即算法计算工作量与方程个数的立方成正比。因此传统的关联函数计算方法在面对高维检索时计算工作量较大，导致索引速度较低。

此外，线性方程组的求解仅为整个关联函数求解过程中的一部分，即线性方程组是关联函数的简化模型，在面对高维检索时，关联函数的求解比线性方程组的求解更复杂，因为简化模型略去了各方程的获取步骤、直线与约束所产生的冗余交点(约束外交点)的取舍步骤(检索维度越高，冗余交点越多)以及从交点到侧距再到关联函数的计算步骤等操作。

综合上述定量和定性分析，将关联函数应用于高维检索时存在效率低下的问题。针对该问题，已有部分学者展开了相关研究，文献[6]提出了基于改进BP神经网络的产品实例分类方法，该方法确实在很大程度上提高了索引速度，但是鉴于训练样本的不足，牺牲了一定的索引精度；文献[12]对此展开了关联函数计算的降维研究，提出了降维规则，但当构建的空间为超多面体时，降维规则仍需进一步完善。

此外，关联函数的计算为定量化计算，而产品属性可能存在多种表现形式，具体可以分为确定数值型、确定区间型、模糊数值型、模糊区间型和模糊概念型。因此，关联函数在面对模糊型参数时还缺乏有效的方法，导致索引精度不高。表1所示为某型号真空泵的部分属性，表中包括多种属性表现形式：抽气速率与运行功率分别为确定区间型和确定数值型，噪声为模糊数值型，环保性能为模糊概念型，故障率为模糊区间型。

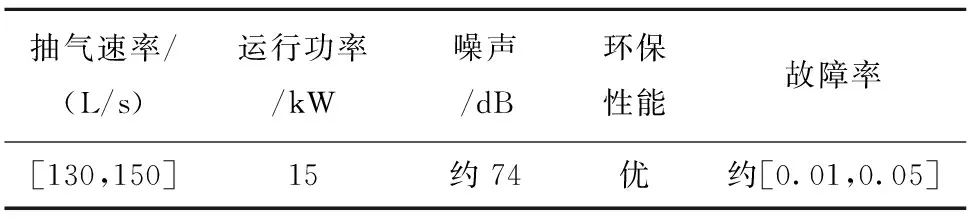
表1 某型号真空泵属性(部分)

针对上述问题，本文将模糊数和层次分析法分别与关联函数相结合，提出模糊关联函数的概念并建立单维关联函数组合相似性度量模型，具体将在第2.2节和第2.3节中展开。

2.1 确定型参数关联函数度量

当产品属性为确定数值型时，该数值即关联函数最优点x0，根据用户需求并结合设计标准，由最优点x0形成理想区间X0，再借鉴可拓学中可拓域与经典域的思想[17]，由理想区间X0外扩形成可行区间X；当产品属性为确定区间值型时，该区间即关联函数理想区间X0，由理想区间可获取最优点x0和可行区间X。根据获取的相关数据，代入式(1)～式(3)即可计算各实例对应属性的关联函数值。

2.2 模糊型参数关联函数度量

目前，关联函数对模糊型参数的度量尚处空白阶段，本文将模糊数的表达方式类比至关联函数计算三要素(最优点，理想区间，可行区间)，提出了模糊关联函数的概念和相关计算公式。

X2]，结合上述区间获取最优点x0。如图1所示为基于模糊数的关联函数计算图示。

(1)模糊数值型参数关联函数度量

根据图1a三角模糊数—关联函数的计算图示，再结合1.1节中侧距的计算公式，本文提出模糊数值型侧距ρ(x,x0,X)表达式如下：

(5)

式中：S△Qxx0表示三角形Qxx0的面积;S表示梯形Qx0xM的面积(其余同理)；-max{S△QX1x0,S△QX2x0}意为取三角形QX1x0面积与三角形QX2x0面积中的较大值，因本文规定X1为离x0较近点，故-max{S△QX1x0,S△QX2x0}=-S△QX2x0。如图2所示为式(5)对应图示。

关联函数需要分别计算可行区间X与理想区间X0的侧距，在面对模糊数值型参数时两者计算方法类似，即将可行区间X替换为理想区间X0，因此本文不再赘述侧距ρ(x,x0,X0)的表达式和计算图示。

将侧距ρ(x,x0,X)和侧距ρ(x,x0,X0)的计算结果代入式(1)与式(3)即可求得模糊数值型参数对应的关联函数值。

(2)模糊区间型参数关联函数度量

根据图1b梯形模糊数—关联函数的计算图示，再结合侧距的计算公式，本文提出模糊区间型侧距表达式如式(6)所示，图3所示为式(6)对应图示。

(6)

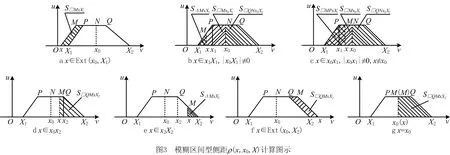
与模糊数值型参数不同，模糊区间型参数的两侧距计算方法并不相同，理想区间X0的侧距ρ(x,x0,X0)的表达式如式(7)所示，图4所示为式(7)对应图示。

(7)

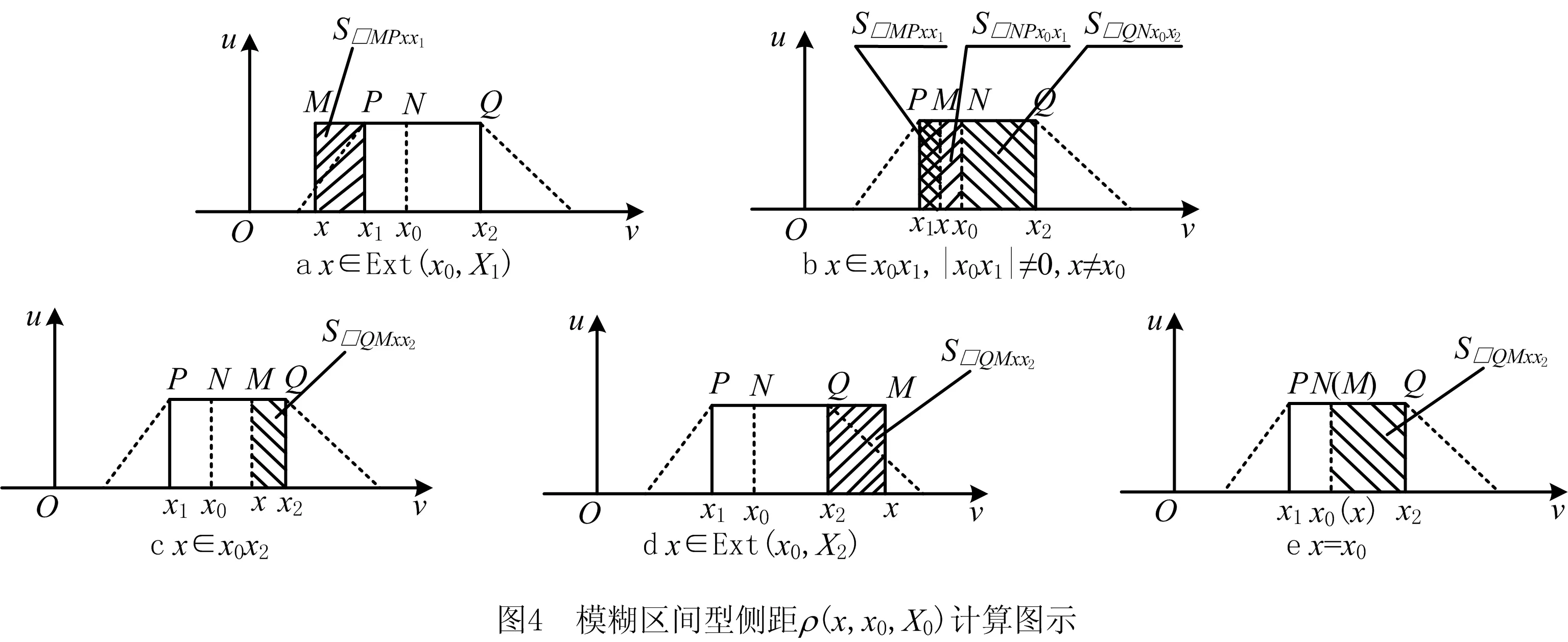
将侧距ρ(x,x0,X)和侧距ρ(x,x0,X0)的计算结果代入式(1)和式(3)即可求得模糊区间型参数对应的关联函数值。

(3)模糊概念型参数关联函数度量

针对模糊概念型参数，本文引入模糊语义转化表(如表2)对模糊语进行量化，再将量化后的值与模糊数值型参数相结合，即用三角模糊数进行表示，再根据对应公式即可求得关联函数值。

表2 模糊语义转化表

2.3 单维关联函数组合相似性度量

根据上文给出的式(5)～式(7)，可以求得不同类型参数间的侧距，然后将所得数值带入式(1)及式(3)中，即可求得实例间各维属性的关联函数值，再结合由层次分析法得到的各属性权重(层次分析法具体步骤可参考文献[22])即可获取目标实例与实例库实例的组合关联函数，以此刻画两者相似度，计算公式如下：

(8)

式中：k(A*)表示组合关联函数;k(Ai)表示属性i的关联函数，wi为对应权重。

因各维属性的关联函数相互独立且单独计算，故从简化模型的角度可得该算法的时间复杂度为O(n)，即算法计算工作量与检索维度成正比，如图5所示为本文所提方法与原方法的时间复杂度对比图。另外，单维关联函数在方程获取，其余计算步骤较全维关联函数简单，且无冗余交点出现，因此该方法在面对高维检索时能够大幅提高索引速度。

3 D-HS索引方法改进及与关联函数融合

第2章提出的模糊关联函数解决了模糊型参数间的相似性度量问题，提高了的索引精度，同时结合层次分析法的单维关联函数组合相似性度量方法提高了索引速度。但该方法在检索时仍需遍历全实例库实例，即检索效用问题仍然存在。鉴于此，本文对1.2节中介绍的D-HS索引进行了基于Sigmoid函数的改进研究，并对两种方法进行了融合。如图6所示为关联函数与D-HS索引的改进与融合图示。

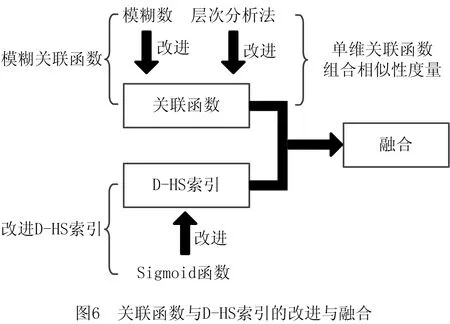
分析1.2节中D-HS索引原理可知，该方法是对实例库实例进行分区间存取，无需进行相似度计算，且受实例库实例数目影响较小，因此该方法不仅效率较高，还能有效避免检索效用问题，但是存在准确率低下问题，具体体现为以下两点：

(1)D-HS索引采用的离散化方法仅适用于属性值均匀或近似均匀分布的情况，当产品属性值非均匀分布时，各区间内实例数目会出现较大的差异，甚至会出现某区间内无实例的情况，该情况下索引准确率会大幅下降。

(2)属性匹配度指代实例库实例的属性与目标实例属性位于相同区间的个数。一般而言，实例间越相似，相同区间个数也会越多，因此属性匹配度可以从整体上反映实例间的相似度，但考虑到存在属性恰好位于区间边缘等特殊情况，若将其作为检索的唯一衡量指标，则存在严谨性不足问题，同样影响准确率。

3.1 基于Sigmoid函数的D-HS索引方法改进

针对实例库实例属性值的非均匀分布现象导致的索引准确率低下问题，本文利用Sigmoid函数对属性值进行非线性变换，该变换能够在不改变数据整体分布及排列情况的前提下，对数据稠密及稀疏区域分别进行扩大和压缩，提高数据的辨识性和划分层级的能力[23-24]。Sigmoid函数表达式为：

(9)

式中：系数β为样本数据的中位数;系数α=ln9/t，其中参数t为样本数据90%分位点及10%分位点到中位点的距离中的较小值。

D-HS索引区别于关联函数的定量化计算，因此当属性为模糊型时可以将其视为确定型。此外，属性为区间型时可以取区间中点代替对应区间进行非线性变换和属性匹配度的计算。

本文以真空泵关键属性—抽气速率为例，验证上述方法对提高属性值非均匀分布时D-HS索引准确率的优势。具体步骤如下：

步骤1调取某真空泵实例库中150种不同型号真空泵的抽气速率为原始数据。

步骤2对原始数据进行以自然对数e为底的对数处理，得到ln数据，再对ln数据进行降序排列。

步骤3根据ln数据计算式(9)中系数α与系数β的值，再将ln数据代入式(9)得Sigmoid数据。

步骤4为统一量纲，将原始数据和ln数据分别进行归一化，得到ln归一化数据和原始归一化数据，并与Sigmoid数据对比。

如图7所示为各组数据对比图，其中图7a～图7c分别代表原始归一化数据、ln归一化数据和Sigmoid数据的散点图和直方图。由上述对比可知，基于Sigmoid函数的非线性变换能够细化数据稠密区间，整合数据稀疏区间，对非均匀分布的数据有较好的处理能力。

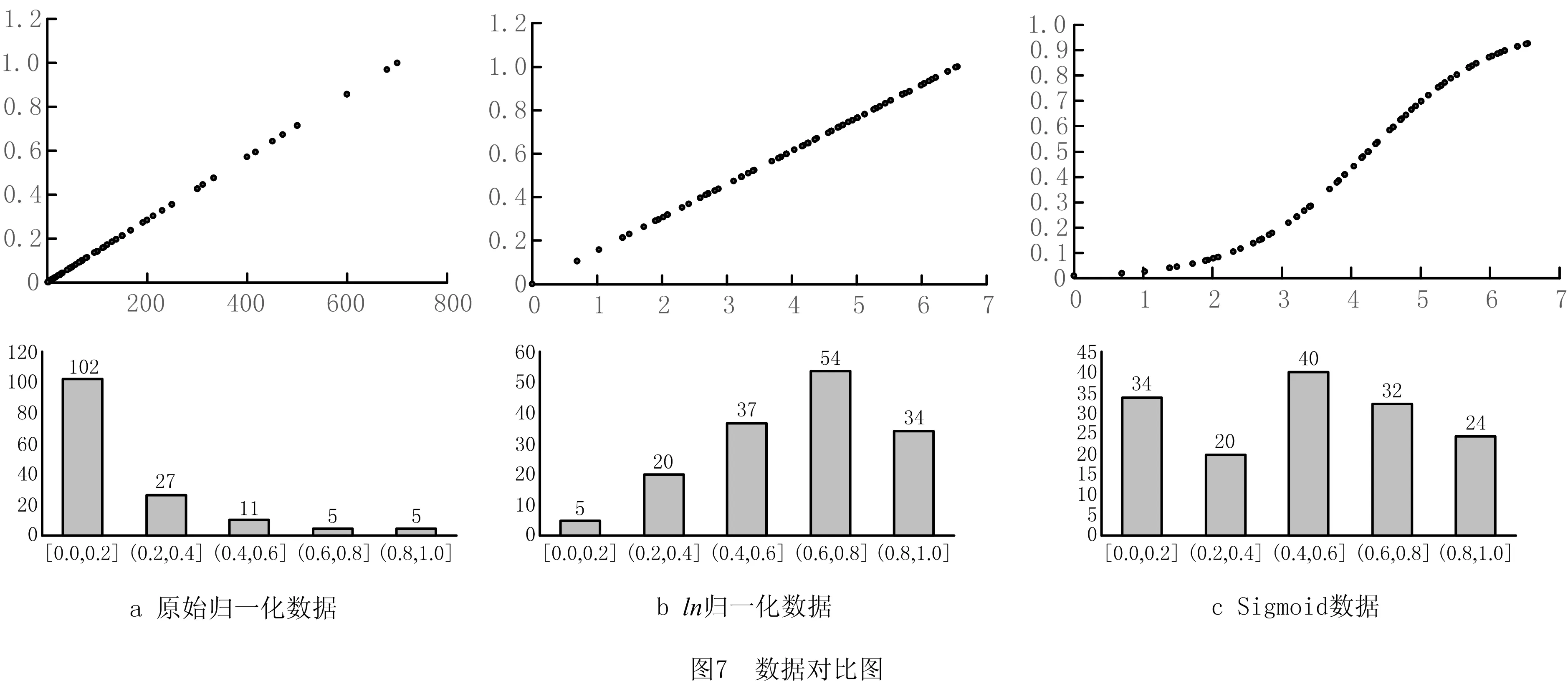
3.2 D-HS索引与关联函数的融合

针对D-HS索引中将属性匹配度作为实例检索的唯一指标而带来的严谨性不足、准确率低下问题，以及关联函数在检索时需遍历全实例库实例而造成的检索效用问题，本文将3.1节中提出的改进D-HS索引方法和第2章建立的结合模糊数和层次分析法的单维关联函数组合相似性度量模型相融合，如图8所示为两者融合示意图。

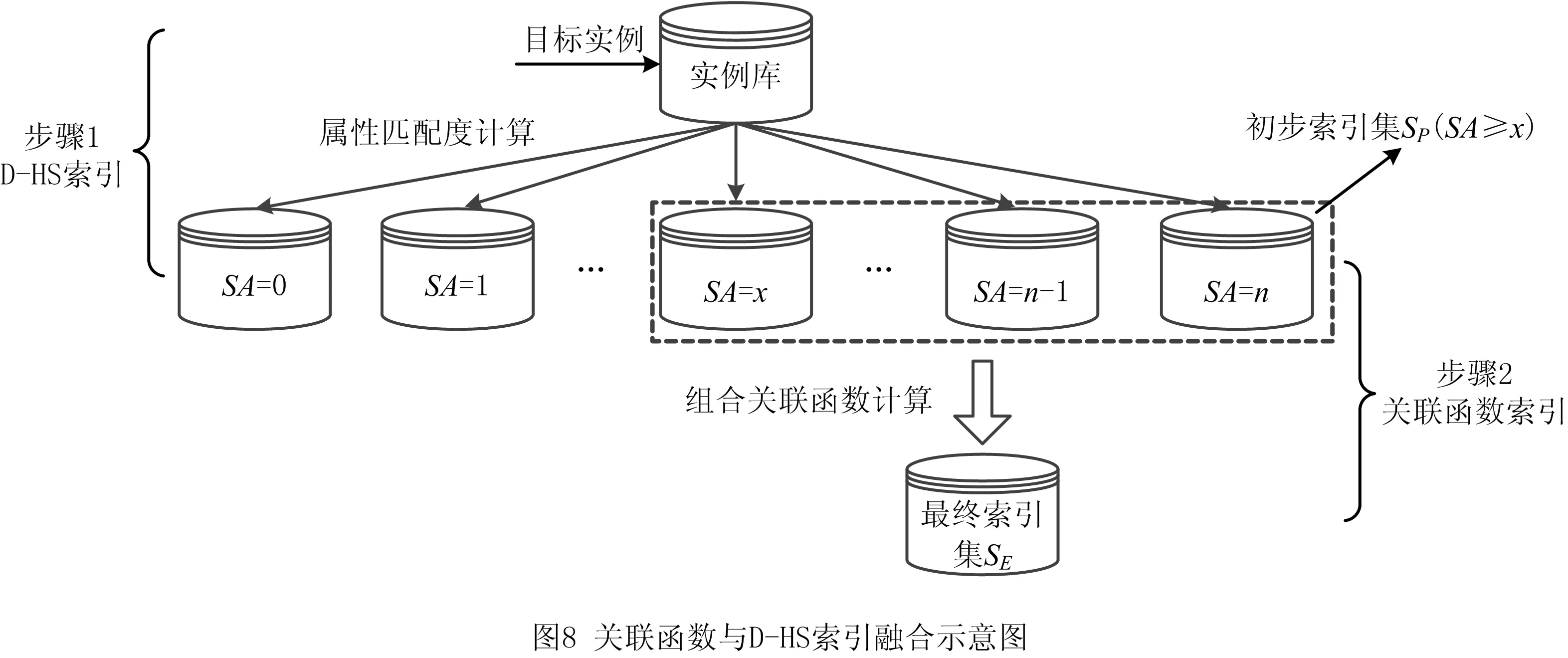
图8中由实例库至最终索引集SE的检索过程共分为两个步骤。步骤1为D-HS索引：根据目标实例计算实例库实例的属性匹配度SA，并分类形成各实例集(SA=0,SA=1,…,SA=n)，再取属性匹配度较高的实例集组成初步索引集SP(根据实例数目而定，一般剔除后60%～后80%，图8中取SA≥x)；步骤2为关联函数索引：根据本文所提的关联函数改进方法，计算SP内实例的组合关联函数，以此获取最终索引集SE。

融合后的检索方法无需计算实例库中每个实例的关联函数，可以在一定程度上避免检索效用问题，同时关联函数的应用解决了传统D-HS索引面临的严谨性不足、准确率低下问题。

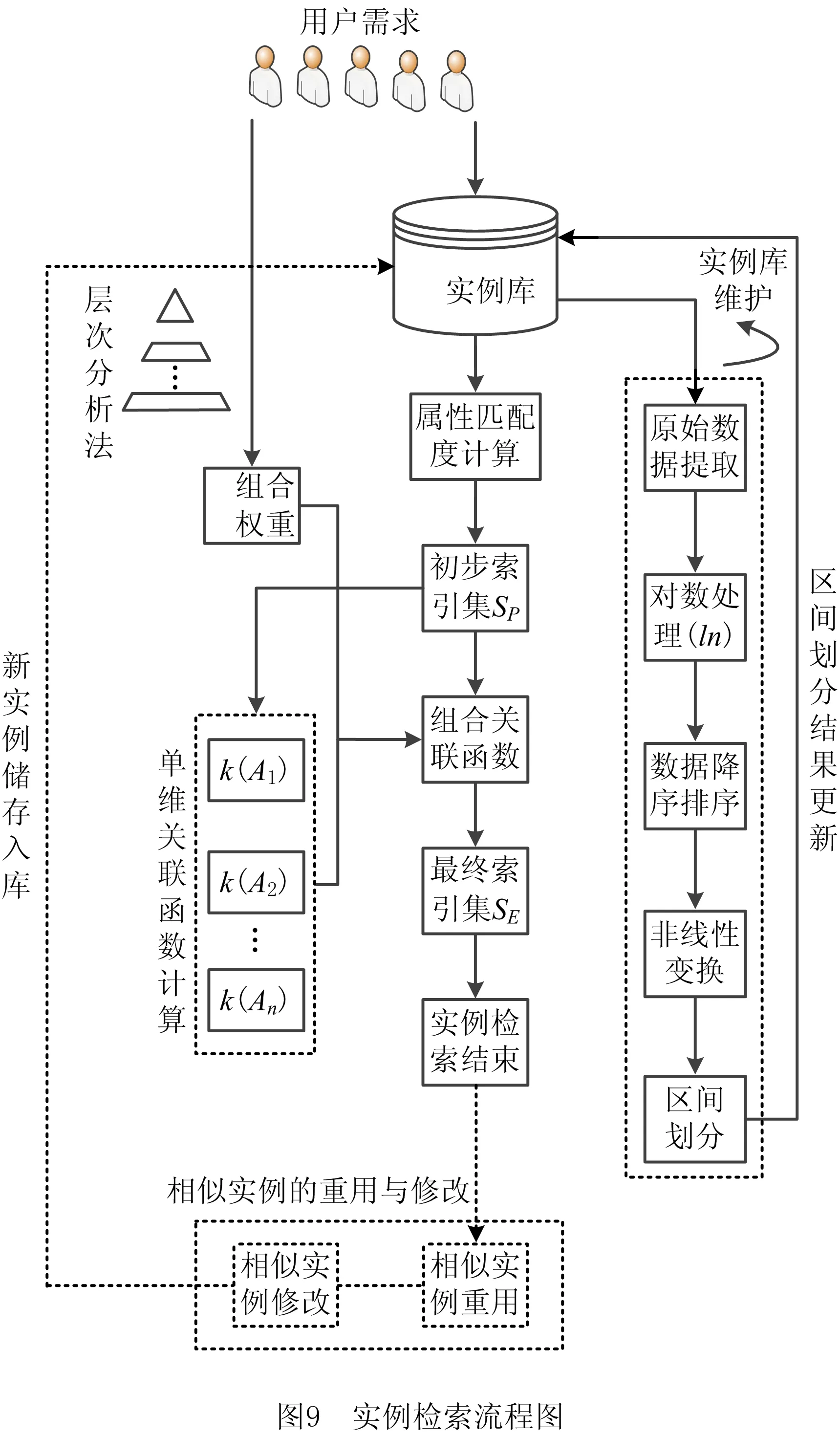
相似实例经检索、重用和修改后可作为新实例重新入库，故在此过程中实例库实例各维属性值的分布情况不断变化，属性值非线性变化后的分布情况亦随之不断变化，因此对应区间的划分不是一成不变的，而对于区间的划分操作可以在实例库更新维护时完成，不必在每次检索前进行。如图9所示为实例检索流程图。

4 实例验证与对比分析

4.1 实例验证

本文以面向用户需求的真空泵检索选型为例对所提方法进行了验证，首先从用户处获取目标实例的相关属性值，并结合层次分析法获取对应权重；然后从实例库中直接调取各型号真空泵的原始数据和非线性变换后的各区间划分情况;最后计算实例库中各实例相对于目标实例的属性匹配度。

表3列出了目标实例属性值及对应权重，其中区间型参数的Sigmoid数据为区间中点对应值。

表3 目标实例属性值及对应权重

图10所示为真空泵关键属性—抽气速率、运行功率和噪声对应的不同类型数据分布图(限于篇幅，未将所有属性全部列出)；表4所示为属性匹配度计算结果。

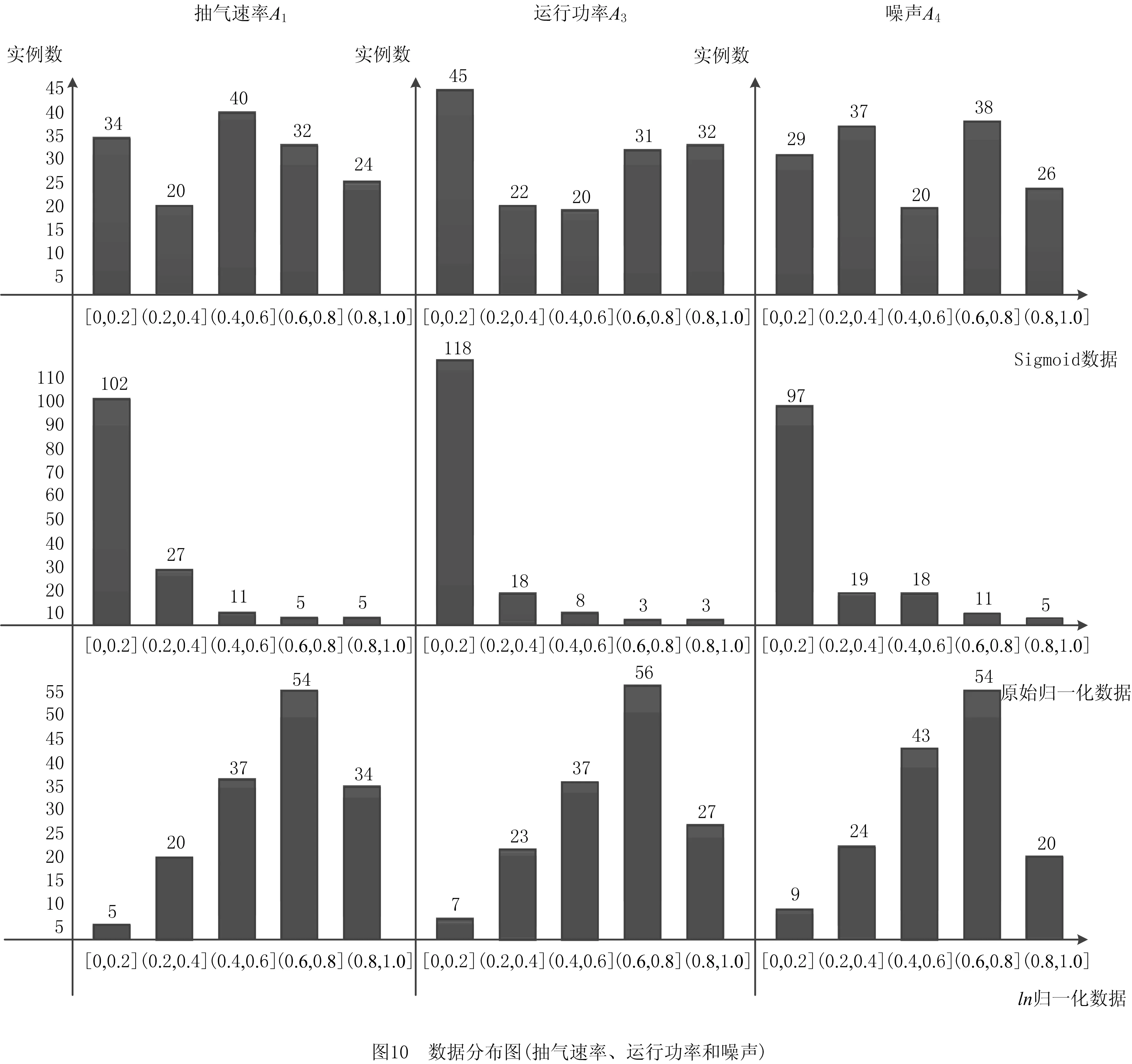
根据表4中各实例的属性匹配度分布情况，本文取SA≥4的相似实例组成初步索引集SP，并依照第2章提出的计算方法获得SP内实例各维属性的关联函数，再与对应权重结合即可求得组合关联函数。表5所示为SP内各实例的单维关联函数和组合关联函数计算结果。

表4 属性匹配度计算结果

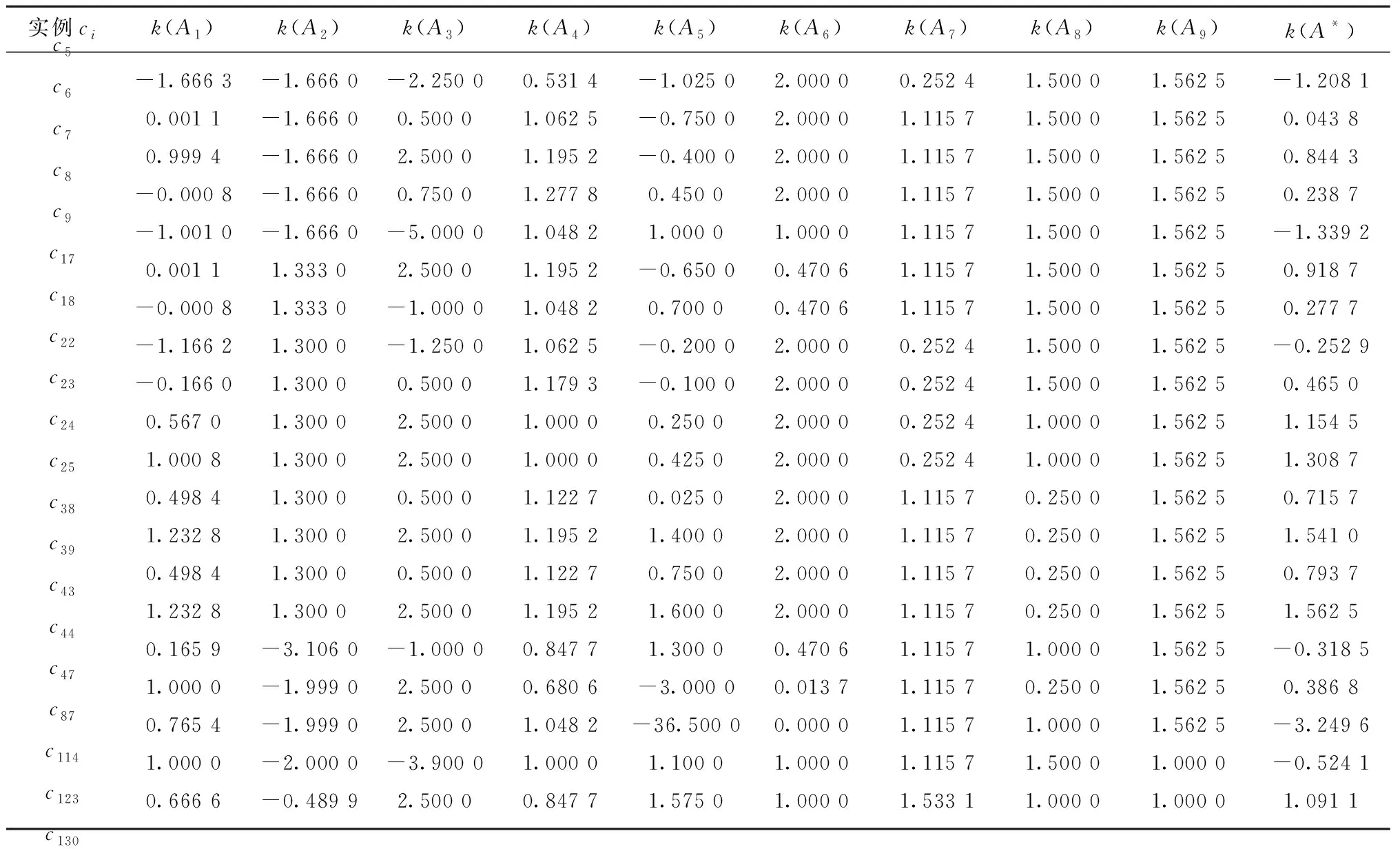
表5 单维和组合关联函数计算结果(初步索引集SP)

比较表5中的组合关联函数k(A*)可知，实例c39,c44与目标实例相似度最高，可优先作为后续实例重用和修改的对象。

4.2 对比分析

(1)模糊关联函数与关联函数

当产品的属性为模糊型时，该属性对应参数之间的差异往往较小，甚至会出现众多实例间无差异的情况，同时参数的分布也会集中在一个区域内，如图11所示为模糊关联函数与关联函数拟合图示。对比图11a与图11b可知，模糊关联函数的提出有助于扩大模糊数间的微小差异，即增加其区分度。

尽管确定型参数也存在部分实例集中的现象，但确定型参数往往分布较广，即参数上下限差距较大，导致可行区间X范围过大，没有实际意义，故无法用模糊关联函数对确定型参数进行相似性度量。此外，关联函数较传统欧式几何距方法、KNN分类检索方法的优势在文献[12]中已作详细讨论，本文不再赘述。

(2)属性匹配度与SP内外组合关联函数

本文提出将D-HS索引中的属性匹配度作为检索的初级指标，以此获取初步索引集SP，再计算其内实例的组合关联函数获取最终索引集SE。为验证该方法的优势，本文计算了全实例库实例的组合关联函数，并与属性匹配度结合做了相应的统计，统计结果如图12所示。

图12中，曲线LAVG表示对应属性匹配度的实例集中各实例组合关联函数平均值的连线(拟合后)。由图12可知：组合关联函数的均值随属性匹配度的增加而增加，因此属性匹配度可以从整体上反映实例间的相似度。

此外，本文对初步索引集SP内外组合关联函数进行了对比，表6所示为SP外部分实例组合关联函数计算结果。

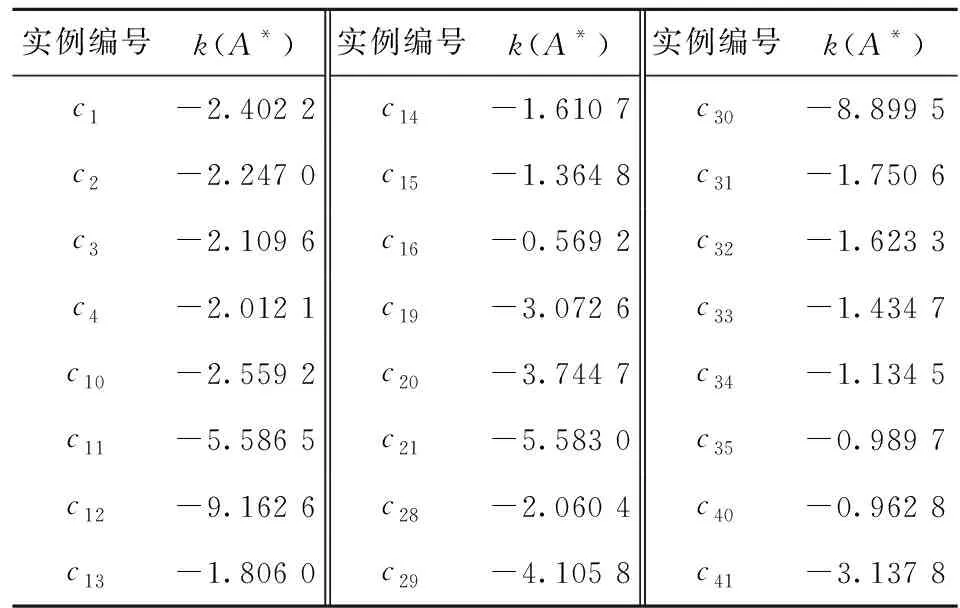
表6 SP外实例组合关联函数计算结果(部分)

对比表5与表6中数据不难发现，SP外实例的组合关联函数整体上小于SP内实例的组合关联函数，尽管表6中存在少数实例的组合关联函数大于表5中部分实例(如实例c35,c40)，但并不影响最终索引集SE的获取。综合上述对比可知，融合关联函数与D-HS索引的检索方法能够在保证索引精度的同时避免部分冗余计算，在一定程度上解决了检索效用问题。

5 结束语

本文将模糊数与关联函数相结合，提出了模糊关联函数的概念，扩大了模糊数间的微小差异，增加了相似实例间的区分度，提高了索引精度；同时结合层次分析法建立单维关联函数组合相似性度量模型，并从定量比较和定性分析的角度论证了所提方法在索引速度上的优势，相较于过去的全维关联函数计算方法，结合模糊数和层次分析法的关联函数在面对高维检索时既保证了索引精度又提高了索引速度。

利用Sigmoid函数对原始数据进行非线性变换，对数据稠密及稀疏区域分别进行扩大和压缩，提高了数据的辨识性和划分层级的能力，有效解决了传统D-HS索引中因数据分布不均导致的索引准确率低下问题。

融合关联函数和D-HS索引，提出根据属性匹配度获取初步索引集SP，再计算SP内组合关联函数获取最终索引集SE的检索步骤，融合后的相似实例检索方法提高了传统D-HS索引的严谨性和准确性，且在确保不出现相似实例遗漏现象的同时避免了关联函数需对全实例库实例进行相似度计算的繁琐，在一定程度上解决了检索效用问题。在检索到与目标最相近的相似实例后需要对该实例进行不同程度的变更，而在变更过程中势必存在变更风险同时带来变更矛盾。因此，后续将针对产品变更风险的预测以及产品变更矛盾的求解两方面做具体展开，以实现产品对市场的快速响应。