基于改进SPEA2算法的铸造并行车间主生产计划
2021-05-07李海龙陈发源计效园李建斌周建新
李海龙,陈发源,计效园+,李建斌,周建新
(1.华中科技大学 材料成形与模具技术国家重点实验室,湖北 武汉 430074;2.华中科技大学 管理学院,湖北 武汉 430074)
0 引言
随着全球制造业数字化、信息化、网络化的不断发展,铸造作为一种传统的高污染、高能耗制造行业面临巨大的挑战和机遇[1]。提升企业生产管理水平,快速响应市场需求,合理制定生产计划成为铸造企业可持续发展的关键。主生产计划是铸造生产计划管理的核心,当前国内铸造企业依靠人工方式制定主生产计划,完成铸造订单在多个相互独立的生产车间上的排产决策。然而现有人工主生产计划,难以在现实不确定生产环境下,综合考虑订单交货期、企业生产效率和生产车间负载均衡等多方面因素,解决具有同种生产工艺不同生产效益的铸造并行车间最优主生产计划问题。同时,人工主生产计划排产效率低下,排产结果缺乏科学性、合理性,严重制约着铸造企业主生产计划管理水平。对铸造企业而言,在保证订单按时交货的条件下合理安排各车间生产计划,既能提高企业生产效率,又能保证各车间生产任务分配的公平性,具有重要的现实意义。
铸造及相关行业的生产计划问题受到学术界和产业界的长期关注,国内外针对该问题已经做了广泛研究。叶虎等[2]研究了铸造热处炉次计划模型,提出了分类与遗传算法相结合的求解方案,有效提高了铸造热处理批计划效率;袁帅鹏等[3]针对炼钢—连铸生产调度问题提出了基于自适应网格择优的非支配排序遗传算法,有效降低了炉次间等待时间。当前铸造生产调度有关问题的研究以具体的铸造生产工序为主,如热处理炉次计划、造型熔炼计划等,而铸造主生产计划从宏观角度制定企业生产排产决策,因此本文考虑以铸造车间整体构建并行机调度模型,求解最优并行车间订单排产方案。毛永年等[4]建立了具有并行制造特征的自动化混流生产线混合整数规划模型,并通过大量随机案例验证了模型的性能;Karimi等[5]研究了多工厂批量供应链调度问题,并提出分支定界法优化排产运输成本和任务延迟成本;Lin等[6]采用线性规划和多级编码的遗传算法求解多工厂下的再生产制造系统的排产问题,并给出了相应的管理指导意见;Jia等[7]研究了以最小化完工时间和电力消耗为目标的并行批处理机调度问题,并采用多目标蚁群算法进行求解;Geyik等[8]提出一套专家规则来准确评价焊工焊接能力,采用启发式方法获得焊工工作负载均衡的焊接计划;孟磊磊等[9]研究了带有阻塞限制的混合流水车间调度问题,通过引入领域搜索改进回溯算法,求解最小完工时间的无关并行机调度。现有并行机调度问题的研究在面对多目标函数求解要求时,往往通过加权法或将其余目标函数转换成约束条件的方式,把多目标函数问题转换成单个目标进行求解。这种方式在实际应用中难以保证确定加权系数或约束条件边界的科学性与合理性。采用经典多目标优化算法解决该问题时,存在对较大规模问题求解效果不理想的问题,同时求得的最终结果为若干Pareto最优解构成的解集,不满足应用条件下希望直接给出最终推荐调度方案的需要。Abido[10]在采用多目标进化算法解决电力调度问题时,使用模糊优选法从求得的Pareto最优解集中挑选出了各目标函数取值折中的方案,这为解决该类问题提供了新的思路。基于这种思路,田启华等[11]采用改进的NSGA-Ⅱ算法(fast elitist non-dominated sorting genetic algorithm)求解产品开发任务调度问题,结合模糊优选法给出了开发成本和执行时间折中的执行方案。由此可见,多目标智能优化算法和模糊优选法相结合,是解决现实铸造复杂约束条件下多目标并行车间调度问题的一种新的途径。
考虑到实际铸造生产过程中的不确定性,往往不能准确给出完成一项订单所需的生产时间,这给主生产计划带来了新的难度。Rostami等[12]研究了模糊环境下带有工作恶化和学习效应的并行机调度问题,并提出了采用多目标分支定界方法进行求解;Liao等[13]研究了基于梯形模糊数的不确定环境下并行机调度问题,并对比了模糊大小对模糊数比较方法的影响;李尚函等[14]研究了基于三角模糊数的柔性作业车间调度问题,在深入分析Sakawa方法的基础上设计了新的排序准则。铸造订单在各车间完工所需的生产时间对主生产计划排产结果具有重要影响,其准确性不可忽略。为此,本文将订单生产时间用三角模糊数表示,以减少模糊生产环境对排产结果的影响,然后建立以订单提前/拖期惩罚成本、车间完工时间和工作负载均衡为指标的多目标整数规划模型,引入模拟退火机制优化强度Pareto进化算法(Strength Pareto Evolutionary Algorithm 2, SPEA2)外部集的环境选择操作和种群的更新方式,以提升其在较大规模空间搜索时的深度和广度,然后通过模糊优选法,从改进的强度Pareto进化算法(Improved Strength Pareto Evolutionary Algorithm 2, ISPEA2)求得的Pareto最优解集中确定出在各目标函数上折中的推荐排产方案,使所提出的模型和算法能够满足实际生产调度的需要。
1 铸造并行车间排产模型
1.1 问题描述
铸造并行车间主生产计划排产是铸造企业在多个生产工艺相同但生产效益不同的铸造车间之间进行订单生产任务分配的一种决策活动。车间的生产工艺一般固定,具有同种生产工艺的铸造车间构成并行车间组。并行车间组内的订单排产问题可以抽象为无关并行机调度问题,属于NP-hard问题。同时现实条件下的排产问题影响更为复杂。为此,本文在研究过程中对该问题模型进行了相应简化。

(1)
三角模糊数之间加减运算可转换为其内部确定值之间的加减运算,同时可以根据其隶属度函数完成如式(2)所示的去模糊化过程。
(2)
为进一步简化铸造并行车间排产模型,作如下问题假设:
(1)车间生产工艺固定,一个车间只能满足一种工艺类型的产品的生产要求;
(2)订单生产工艺固定,且不可拆分;
(3)所有订单必须分配给车间生产,但允许某些车间没有生产任务;
(4)车间生产过程连续且不可被抢占。
基于上述假设条件,可以将铸造生产车间按照工艺划分到不同的并行车间组,一个车间只能属于一个并行车间组。如图1所示为确定并行车间组的流程图。
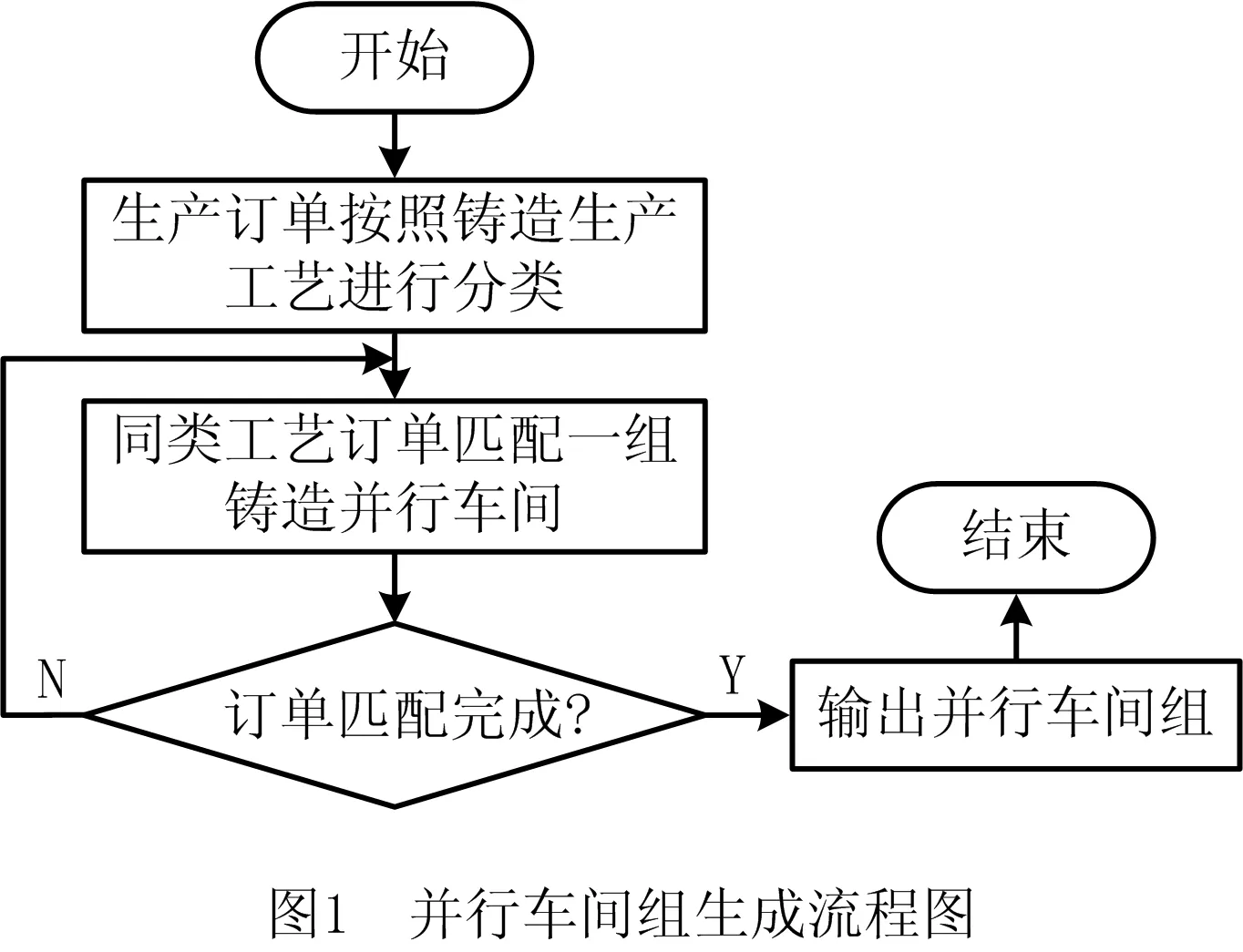
1.2 数学模型
(1)索引和参数
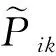
(2)决策变量
(3)
(4)
(3)目标函数与约束条件
(5)
minF2=max(C1,C2,…,CM);
(6)
(7)
(8)
(9)
(10)
j=1,2,…,N;i≠j;
(11)
i=1,2,…,N;i≠j;k=1,2,…,M;
(12)
(13)
(14)
式(5)~式(7)为目标函数,其中:式(5)为最小化订单提前/拖期惩罚成本,式(6)为最小化所有车间中最大的总完工时间,式(7)为最小化各车间完成本次分配的订单所需的时间的方差;式(8)和式(9)分别为计算订单提前或拖期完成时,提前或延误的天数;式(10)保证一个订单只被分配到一个车间中,并由该车间单独完成;式(11)用来决定分配给相同车间完成的订单之间的先后次序关系;式(12)表示订单i在车间k上的完工时间等于订单i之前的订单所需加工时间之和,加上订单i的加工时间和完成车间原有剩余工作所需时间;式(13)表示车间k的总完工时间等于分配给车间k所有订单加工时间之和加上完成车间原有剩余工作所需时间;式(14)为计算各车间完成本次排产所分配的订单需要的时间。
2 基于ISPEA2与模糊优选法的求解方案
SPEA2算法作为一种基于Pareto的元启发式算法,在求解多目标优化问题时具有良好的性能[15]。本文基于所提出的数学模型,设计了离散编码形式的ISPEA2算法,为提高其在离散解空间搜索的深度和广度,通过引入模拟退火机制改进算法外部集的环境选择操作和种群的更新方式,以一定概率接受适应度较差的解,控制外部集和种群的收敛速度,避免算法过早陷入局部最优,求解出并行车间订单排产的Pareto最优解集。Pareto最优解集中的任意一个解都不能在所有目标函数上完全支配其他解,在实际应用条件下,从中挑选合适排产方案的决策过程较为复杂。为此,本文采用模糊优选法,以Pareto最优解在各目标函数上的均衡优化程度为指标,计算并从改进后算法所求得的Pareto最优解集中选出一个在各目标函数上折中的解作为最终推荐排产方案,从而更好满足实际生产排产的需要。如图2所示为求解方案流程示意图。
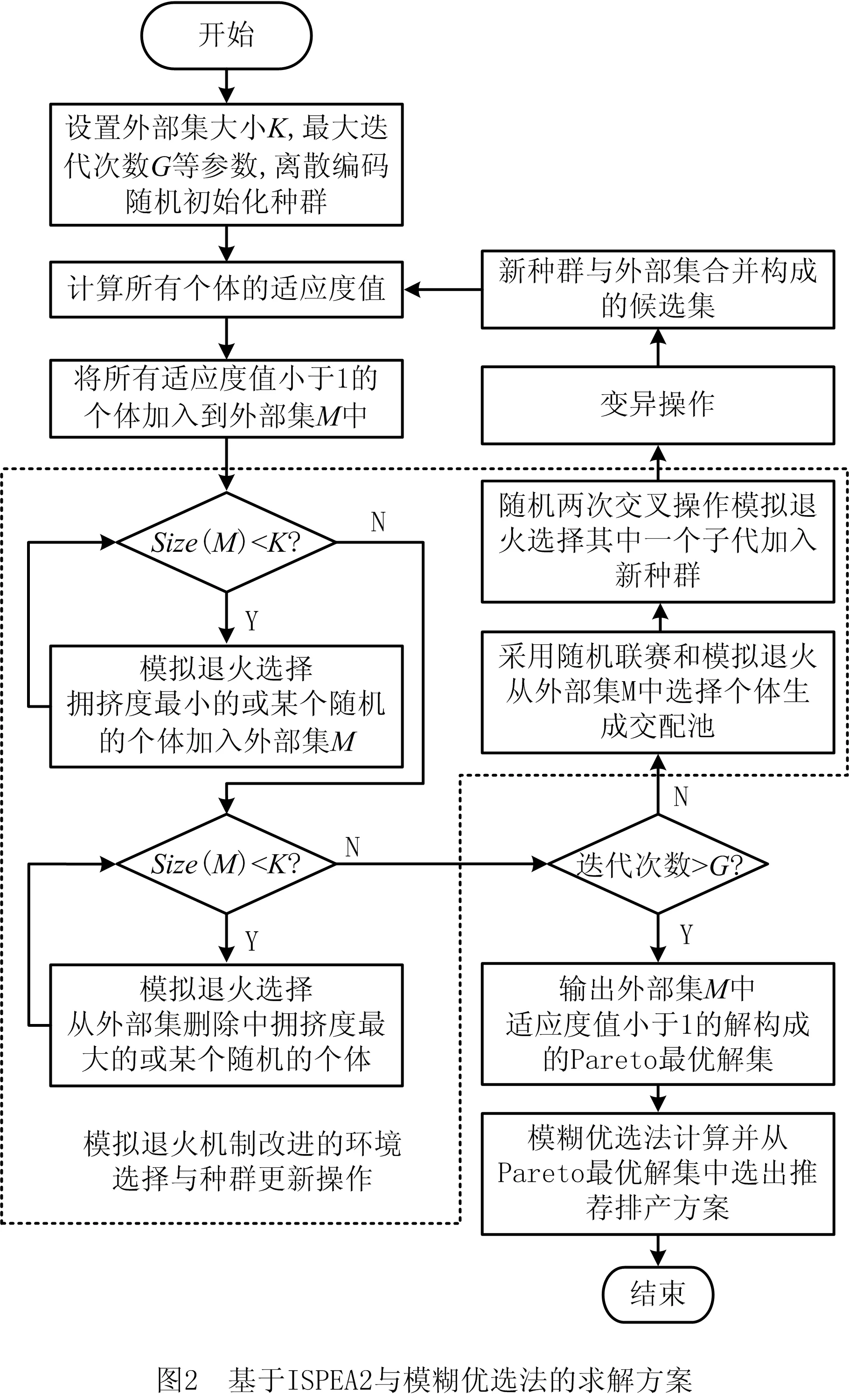
2.1 离散编码
ISPEA2算法中种群个体采用离散整数的形式进行编码,储存在一条由整数1~N和1~M-1个0组成的染色体向量中,其中1~N表示待分配的订单编号,0表示将左右两边的订单分配到不同的车间中。在解码过程中,分配给相同车间的订单的先后顺序由编码向量中从左到右的订单编号顺序决定。如图3所示为将10个订单分配给3个车间的排产方案编码和解码示意图。车间A依次完成订单6、3、8,车间B依次完成订单2、7、9、5,车间C依次完成订单10、4、1。
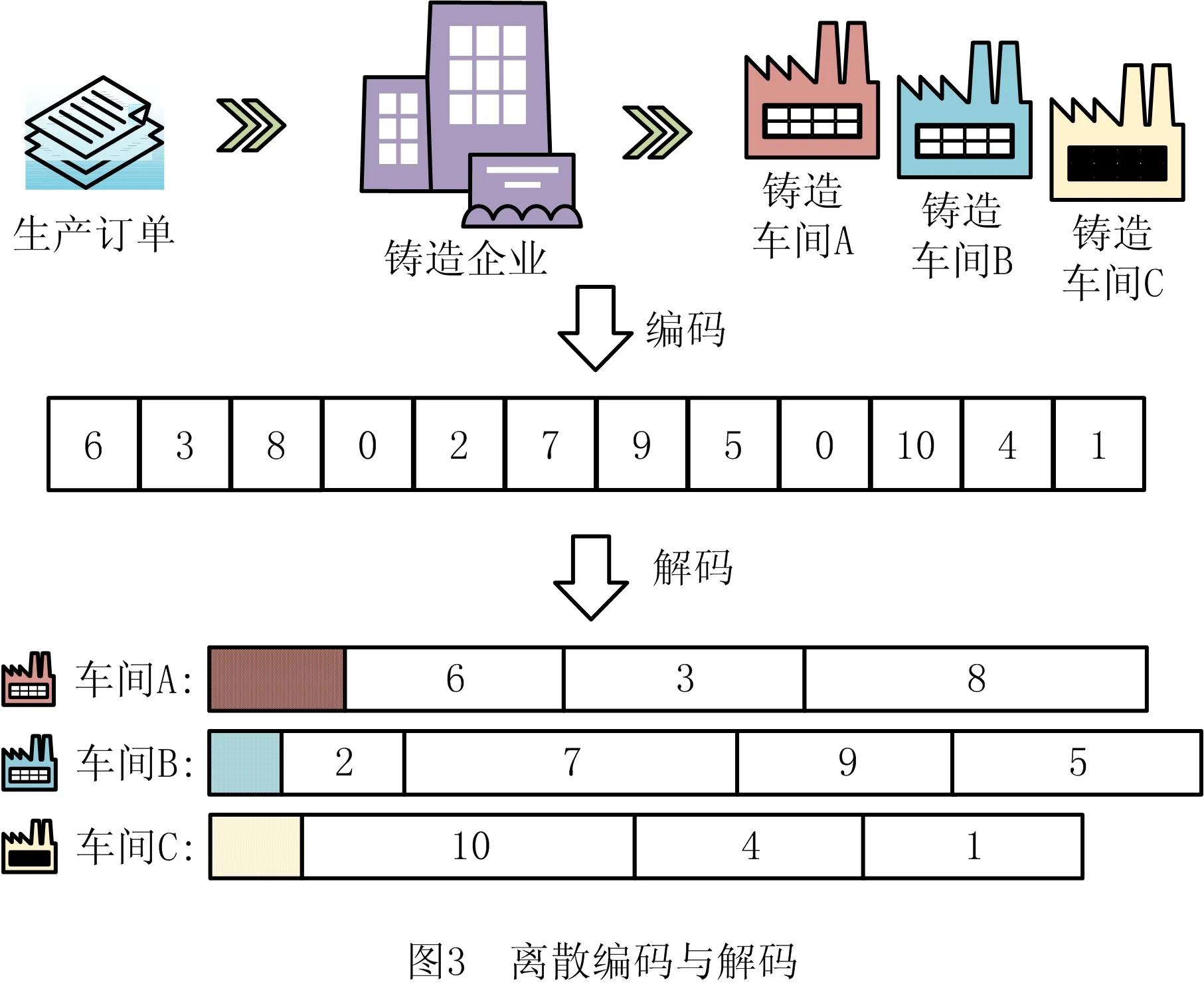
2.2 交叉变异操作
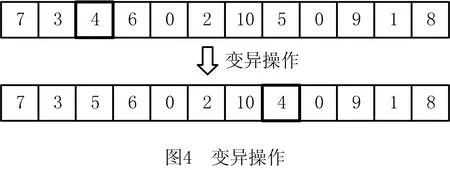
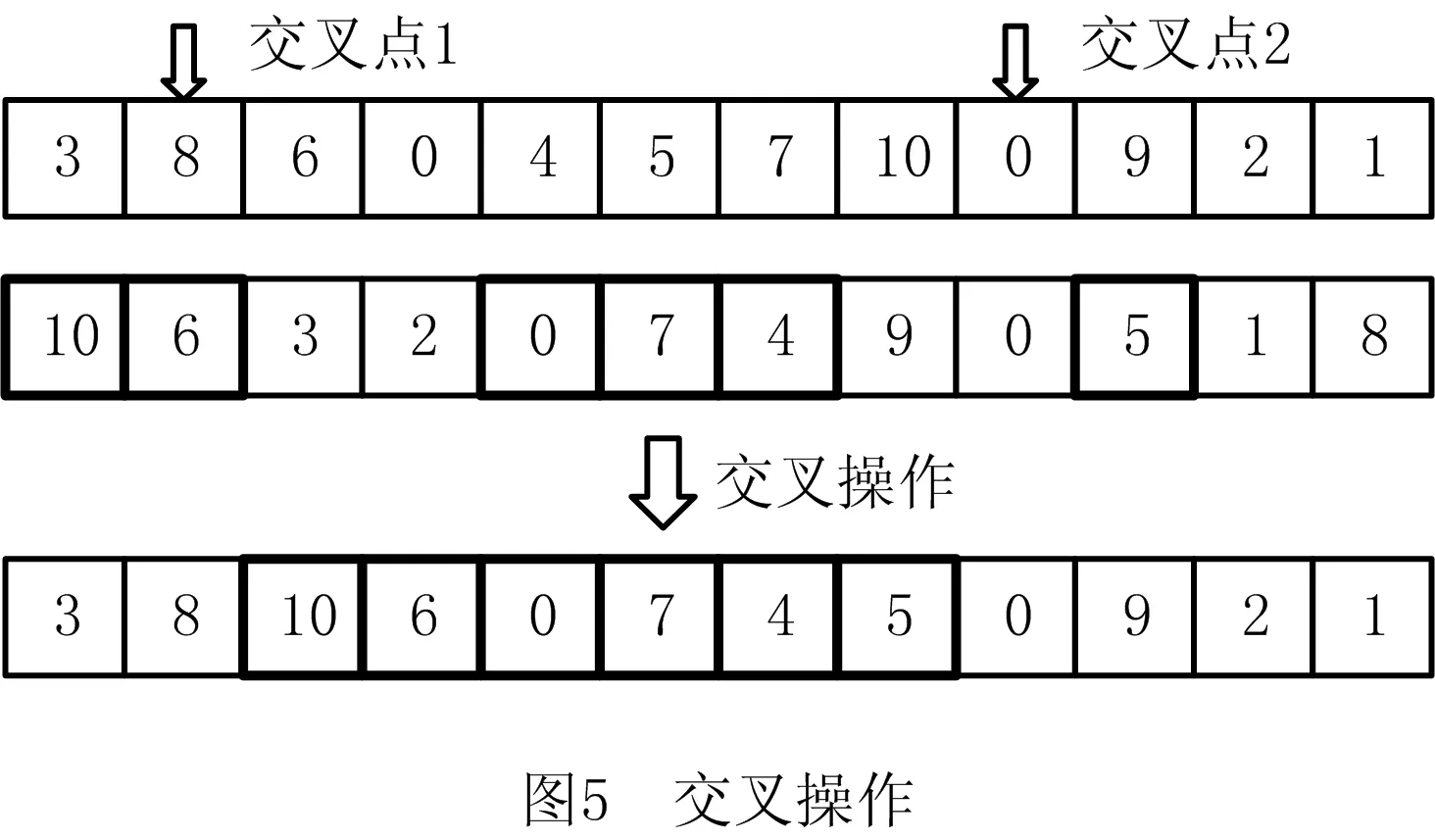
为保证ISPEA2算法在离散解空间的搜索性能,设计了如图4和图5所示的变异和交叉操作。在进行变异操作时,首先在原染色体向量中随机选取两个位置,然后通过交换这两个位置上的基因产生变异后的新个体。交叉操作首先在父本基因向量上随机选择两个交叉点,交叉点两端的基因将直接复制到孩子个体染色体向量中,剩余的基因将按照在母本染色体向量中的排列顺序依次继承到孩子个体染色体向量中。
2.3 模拟退火选择
在外部集中添加和删除个体、生成交配池以及交叉操作产生新种群过程中,需要在两个候选个体之间进行一次模拟退火选择。模拟退火选择步骤如下:
步骤1计算个体a和b的适应度值Fa、Fb。
步骤2判断Fa是否大于Fb。若否,则选择个体a。若是,则随机生成(0,1]上某个概率值p,转步骤3。
步骤3判断公式随机概率p是否满足式(15)和式(16)所示条件。若是,则选择个体a;否则选择个体b。其中:t和T分别为当前温度和初始退火温度,μ为退火速率,i为算法当前迭代次数。
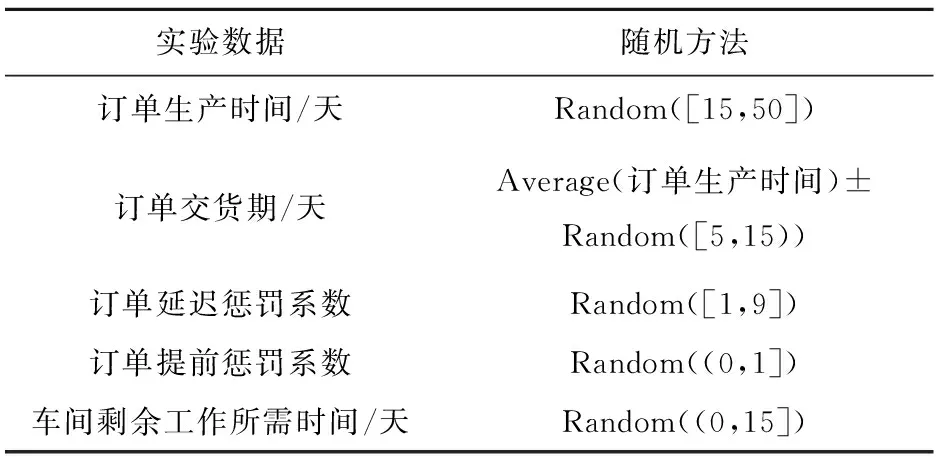
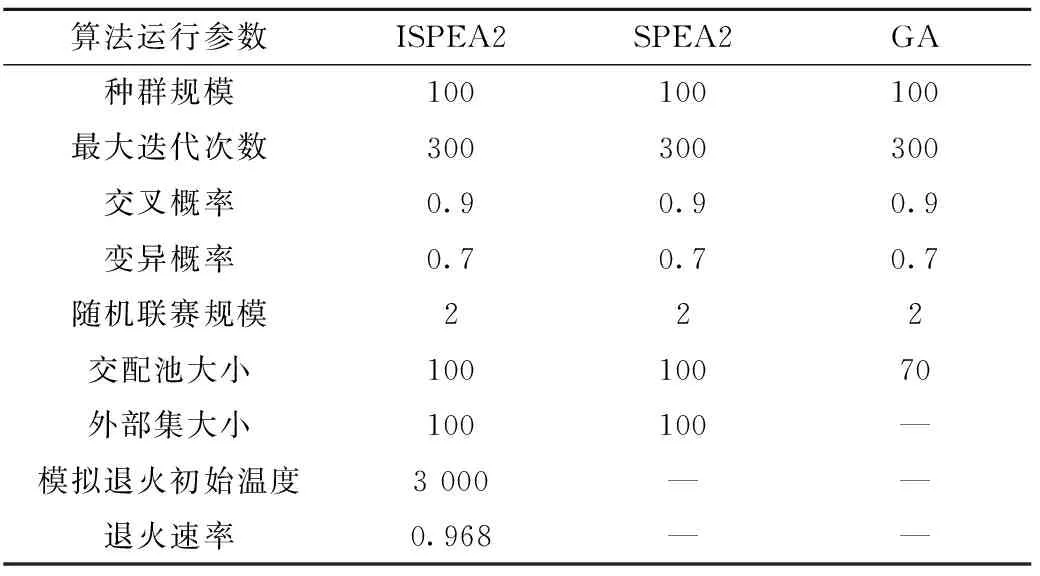
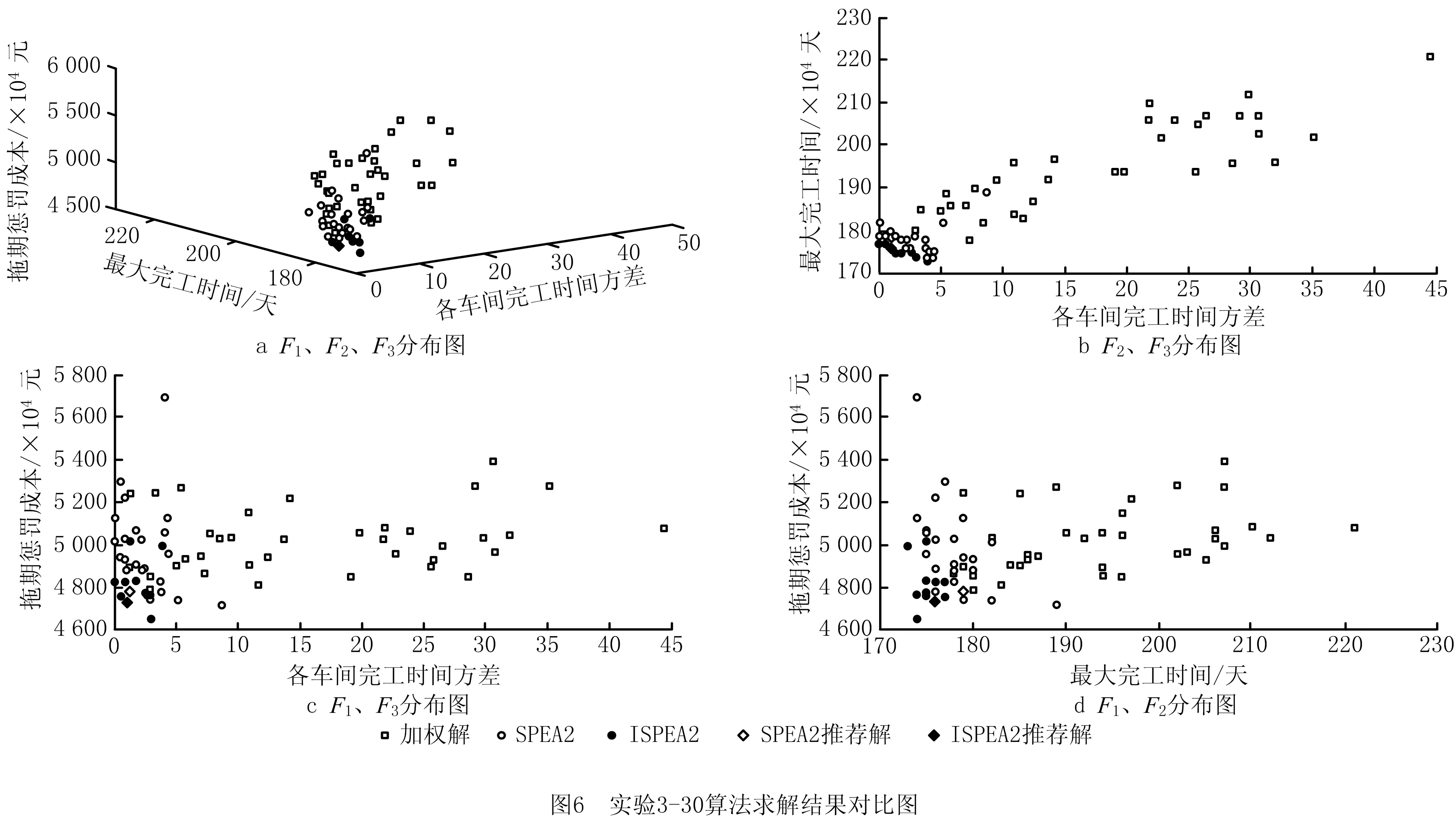
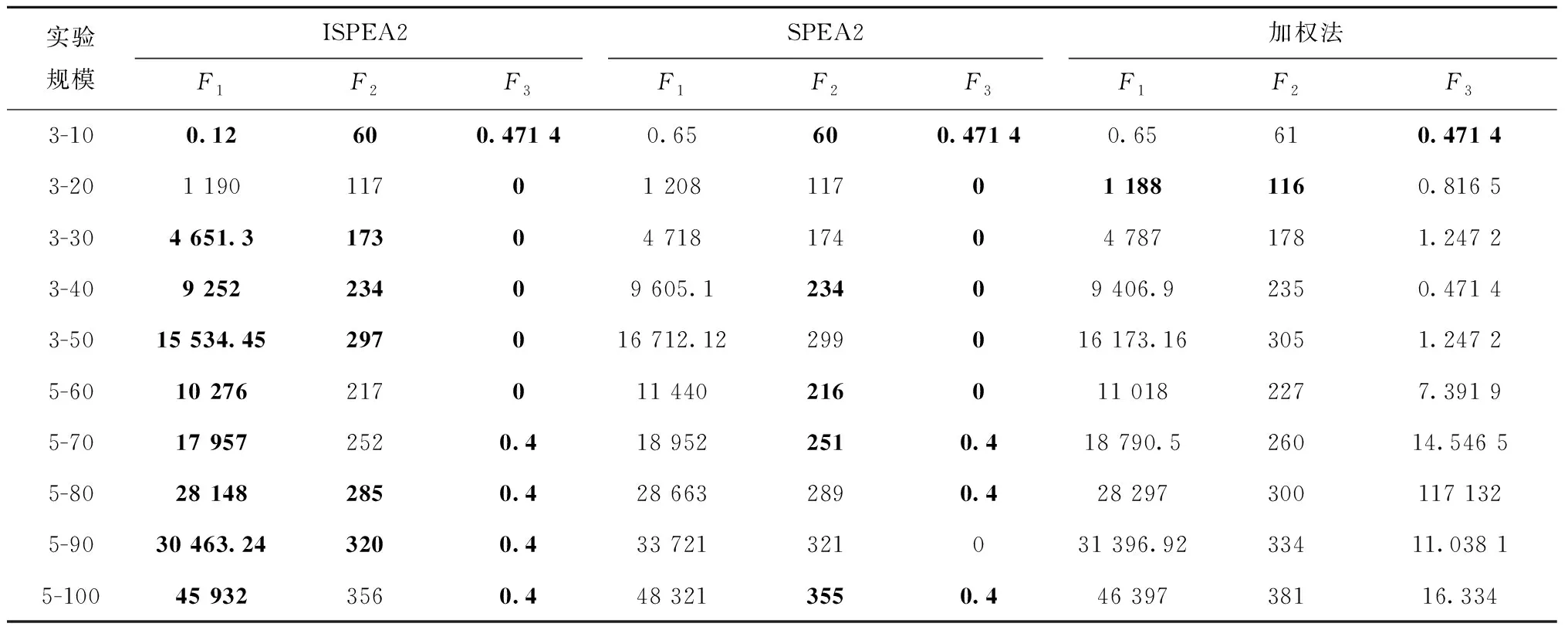
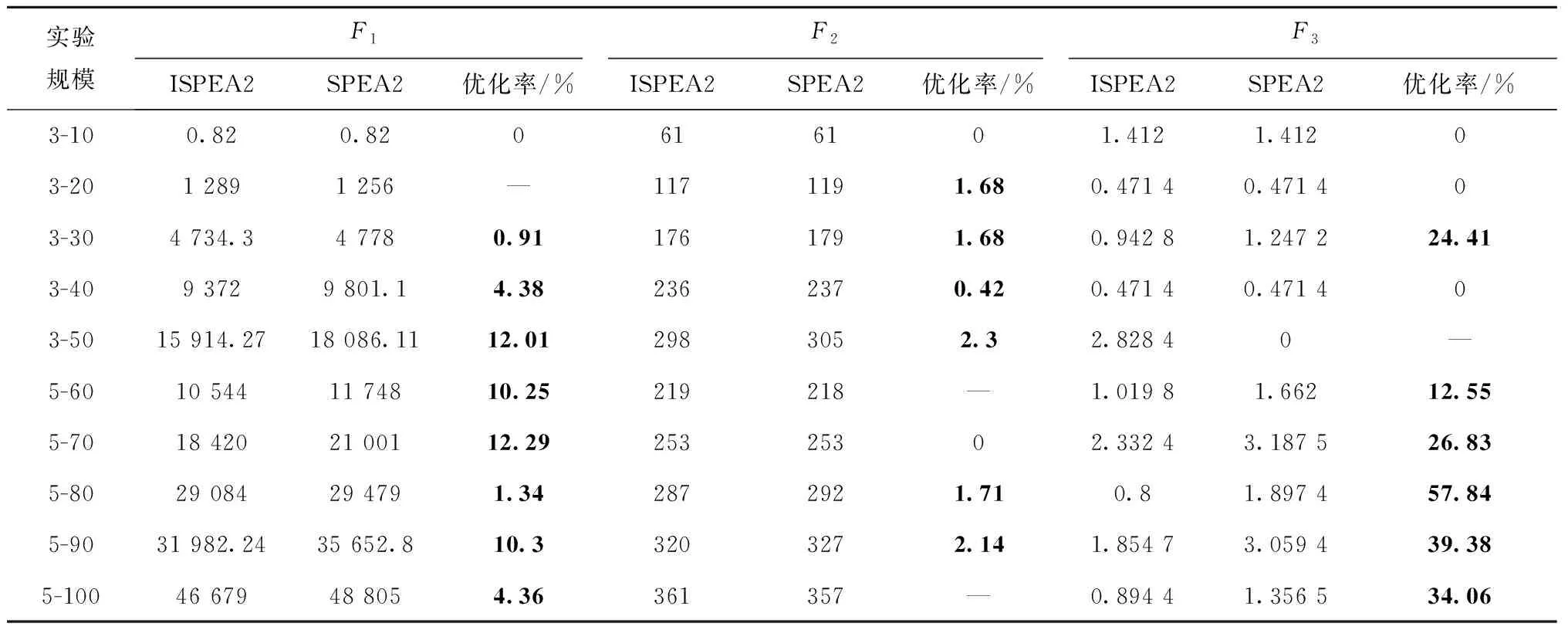
p (15) t=μi×T。 (16) ISPEA2算法求解结果为一个由若干互不支配的Pareto最优解构成的解集,为进一步从该解集中挑选出在各个目标函数上表现均衡的折中推荐排产方案,本文选用模糊优选法,通过计算Pareto最优解各目标函数值与Pareto最优解集中该优化目标上最优解和最差解的函数值的接近程度,作为各Pareto最优解的评价指标,从而判定其在各目标函数上的均衡优化性能,保证从Pareto最优解集中选出的推荐排产方案的科学性与合理性。具体计算方法如下:如式(17)所示,首先分别求出Pareto最优解集Ω中的解i在各个目标函数j上的比重δij,其中FjMIN和FjMAX分别为Pareto最优解集Ω在目标函数j上最优解和最差解的目标函数值。当解i在目标函数j上的函数值等于FjMIN时比重δij为1,等于FjMAX时比重δij为0。 (17) 然后,经过式(18)所示的标准化操作,计算得出Pareto最优解i的评价指标δi。评价指标δi越高,说明该解在各目标函数上的综合表现越好。因此,本文将Pareto最优解集中评价指标最高的解确定为最终推荐排产方案。 (18) 为验证所提出模型和算法的有效性,设计了10组不同规模的仿真实验,其中并行车间数和待分配的订单数分别为:3,10;3,20;3,30;3,40;3,50;5,60;5,70;5,80;5,90;5,100。仿真实验数据采用如表1所示的方法随机生成。将改进后的ISPEA2算法与改进前的SPEA2算法、加权法进行对比,算法的运行参数如表2所示。其中加权法采用遗传算法(Genetic Algorithm, GA)进行求解,3个目标函数分别与对应的权重λ1、λ2、λ3相乘,然后相加转化为单目标函数进行求解。其中,λ1、λ2分别取[1,8]、[1,9-λ1]内的整数,且λ1+λ2+λ3=10,组成较为全面覆盖目标函数权重可能分布的36个加权法解。 表1 仿真实验数据 表2 算法运行参数 为直观展示算法对比结果,选取规模为3-30、3-50、5-70和5-90的4组仿真实验数据绘制ISPEA2、SPEA2和加权法求解结果对比图,如图6~图9所示。 从三维空间和二维平面上解的分布可以看出,改进后的ISPEA2算法求得的Pareto最优解的分布更靠近坐标轴和原点,解的支配性明显优于SPEA2和加权法。随着求解问题的规模增大,这一趋势也更加明显。3种算法在10组仿真数据上运算结果对比如表3和表4所示。其中,表3对比了3种算法所求得的解集中的解在3个目标函数F1、F2和F3上所能取到的最小值,表4分析了SPEA2算法改进前后求得的推荐解在各目标函数值上的优化率。优化率ε根据公式(19)计算: ε=|FSPEA2-FISPEA2|÷FSPEA2×100%。 (19) 式中FSPEA2和FISPEA2分别表示SPEA2算法和ISPEA2算法推荐解的各目标函数值。 从表3可以看出,除了3-20、5-60和5-70实验中在部分目标函数上的最小值略高于3种算法所能求得的最小值以外,ISPEA2算法在其他实验规模的对比中均能取到最低值,进一步说明了其所求得的解相对于另外两种算法的支配性。从表4可以看出,改进后的算法求得的推荐解和改进前的算法相比,各目标函数值均得到有效优化,其中目标函数F2得到有效降低,目标函数F1、F3优化效果显著,最高减少了改进前算法的57.84%。 结合表3和表4可以看出,ISPEA2算法在较大规模问题上的求解效果与小规模问题相比更加明显。实验3-10、3-20中,由于问题搜索空间规模较小,3种算法均能有效的求得3个目标函数上的最小值,改进后的ISPEA2算法求得的推荐解优化效果不明显;随着问题规模增加,所提出的模拟退火改进策略有效避免了ISPEA2算法在搜索过程陷入局部最优,使求出的3个目标函数最小值明显小于另外两种算法,推荐解的优化效果也随之更加显著。从总体来看,改进后的算法所求得的解在完工时间目标上有所降低,而生产惩罚成本明显下降、车间负载均衡程度得到显著提升。 表3 三种算法在各目标函数上的最小值对比 表4 SPEA2算法改进前后推荐解目标函数值优化率 为合理制定模糊生产环境下的铸造企业并行车间主生产计划,将订单生产时间用三角模糊数表示,从订单交期准确率、车间工时利用率和负载均衡性3个方面综合考虑,建立了铸造并行车间订单排产多目标整数规划模型,提出了离散编码形式的ISPEA2算法,通过引入模拟退火策略改进算法外部集的环境选择操作和种群的更新过程,求解出并行车间订单排产的Pareto最优解集,然后通过模糊优选法计算,从中选出折中的推荐排产方案。通过多个规模的仿真实验验证了所提出模型和求解算法的有效性。实验结果表明,改进后的ISPEA2算法求出的Pareto最优解的支配性明显优于改进前算法和加权法所求得的解,同时,最终确定的推荐排产方案与改进前相比订单提前/拖期惩罚成本、车间完工时间和负载不均衡程度均有效降低。 铸造并行车间主生产计划未来可能的研究方向包括以下两点: (1)当前模型考虑的铸造车间只能生产一种工艺类型的订单,而实际情况下可能存在特殊车间能够完成多种不同类型的生产任务。考虑该特殊车间的并行车间排产问题更具挑战性。 (2)实现铸造主生产计划求解方案与铸造企业现行数字化信息化生产管理软件的集成,推动铸造行业智能化发展。2.4 模糊优选法
3 仿真实验
3.1 实验设计
3.2 实验结果与分析

4 结束语
