基于神经网络和再制造因子的再制造机床可靠性分配方法

杜彦斌，吴国奥，许 磊

(1.重庆工商大学 制造装备机构设计与控制重庆市重点实验室，重庆 400067；2.重庆工商大学 国家智能制造服务国际科技合作基地，重庆 400067；3.重庆工商大学 管理科学与工程学院，重庆 400067)

0 引言

再制造是循环经济再利用的高级形式，它将传统的“线性”制造模式转变为“闭环”制造模式。在当今环境污染和资源紧缺问题日益严峻的背景下，再制造产业的发展受到国内外的广泛关注[1]。作为发展中国家，我国的再制造产业虽然起步较晚，但发展政策和措施不断完善。2016年，国家工信部公布了包括工程机械、专用设备、机械、机床等领域的53家企业为第二批机电产品再制造试点单位，到2019年《再制造产品目录》已更新至第八批，涵盖了更多的产品名称及型号[2]。其中，机床再制造是指利用可再制造性分析、表面工程及再制造工艺、机床性能恢复与升级、再制造质量管理和控制等技术，充分挖掘废旧机床的剩余价值，使其经过再制造与综合性能提升后，在技术和性能指标上能够达到甚至优于新品的制造模式[3]。我国作为传统制造业大国，机床保有量已居世界第一位，每年有大量机床面临报废[4]。此外，改革开放以来，国内企业从国外引进了大量高端机床装备和生产线，这些高端机床大都价格昂贵，且经过多年服役，也陆续进入报废期。由此可见，我国发展机床再制造的市场前景广阔。

不同于传统制造，机床再制造的主要过程由废旧机床回收、拆解与清洗、检测与分类、再制造加工及机床整机再装配组成[5]。机床再制造过程中存在的时间、原料、路径与工艺等不确定性，给再制造机床质量管理带来了挑战。虽然我国机床再制造市场潜力巨大，但由于发展初期技术水平有限和管理制度不完善，部分质量不达标的产品流入市场，导致消费者对再制造产品的接受度一直不高[6]。确保再制造机床的可靠性是提升客户对再制造机床认可的有效途径，也是提高再制造企业综合竞争力的必要手段[7]。可靠性分配是指从系统角度出发，综合考虑各种影响因素，将可靠性指标自上而下地分配到各个零部件，从而实现系统整体可靠性的优化[8]。可靠性分配与优化是可靠性设计的关键环节，也是保障机床装备质量与可靠性的重要手段。

近年来，国内外学者围绕再制造机械装备的可靠性开展了研究。文献[9]研究了风力涡轮机运维过程中再制造与可靠性之间的关系，得出在产品使用终期(End of Use，EOU)阶段，可靠性高的设备再制造所需投入的成本更小，所需工艺更简单;文献[10]考虑了回收产品的失效形式，建立了再制造工艺规划的可靠性与成本模型，采用遗传算法对再制造工艺优化问题进行了分析与求解;文献[11]同时考虑了机床的几何误差和热致误差对于加工精度的影响，建立了几何误差—成本模型和几何误差—可靠性模型，并结合改进的遗传算法进行精度分配，可提升机床的加工精度及可靠性;文献[12]从失效分析和可靠性设计、再制造过程可靠性、再制造装备服役可靠性三大方面总结了机械装备可靠性的研究成果，探讨了机械装备可靠性研究存在的问题;文献[13]考虑到再制造工艺方案的不确定性，建立了一种基于改进T-S模糊神经网络的再制造工艺方案优化决策模型，并利用MATLAB仿真得到了最优的再制造工艺方案;文献[14]用可靠性来反映部件服役周期内性能衰退特征，并采用最小二乘法及平均秩次法拟合部件可靠性，得到其最优主动再制造时机;文献[15]针对偏心轴再制造涂层的优化与可靠性问题，基于响应面优化分析了设计变量对涂层性能的影响规律，并引入六西格玛分析方法以提高再制造设计方案的可靠性。

虽然已有许多学者从多个角度出发，对再制造机床的可靠性进行了研究，但目前的研究方向较为分散，针对再制造机床可靠性建模与分配的研究较少。再制造机床结构复杂，其可靠性受到诸多因素的影响。同时，各组成部件的可靠性提升也受不同再制造工艺影响，需要考虑的因素更多。而传统的可靠性分析优化方法不能较好地适应再制造机床结构复杂，以及再制造过程中的不确定性等特点。针对目前再制造机床可靠性提升的难题，为了完善机床再制造可靠性研究的相关理论，进一步推动机床再制造产业发展，本文引入故障树、神经网络等理论，提出一种基于神经网络与再制造因子的再制造机床可靠性逐级分配方法，为提升再制造机床可靠性提供理论支撑。

1 再制造机床可靠性分配的流程

再制造机床的可靠性分配是指综合考虑再制造过程对机床可靠性提升的影响，将再制造机床可靠性目标合理分配给构成再制造机床的各零部件。然而，再制造机床作为复杂系统，其结构复杂，整机往往由多个子系统构成(如变速机构、进给机构、主轴箱、刀架、数控系统、润滑系统、冷却系统等)，每个子系统又包含多个零部件[16]。同时，在再制造过程中，考虑不同子系统或零部件的剩余寿命，回收的零部件又被分为直接重用件、可再制造件、材料回收件、直接废弃件。不同回收零部件的再制造工艺不同，可靠性提升需要考虑的因素也更多，直接将总体可靠性分配至各个零部件较为困难。

针对再制造机床可靠性分配问题，通过分析再制造机床结构，将再制造机床系统划分为多个子系统及零部件。可靠性分配过程中，各层级可采取不同的分配方法，以适应再制造机床结构及再制造工艺特点。再制造机床可靠性逐级分配过程如图1所示，主要包括可靠性模型的构建、可靠性目标的决策、系统级—子系统级的可靠性分配以及子系统级—零部件级的可靠性分配4个步骤。

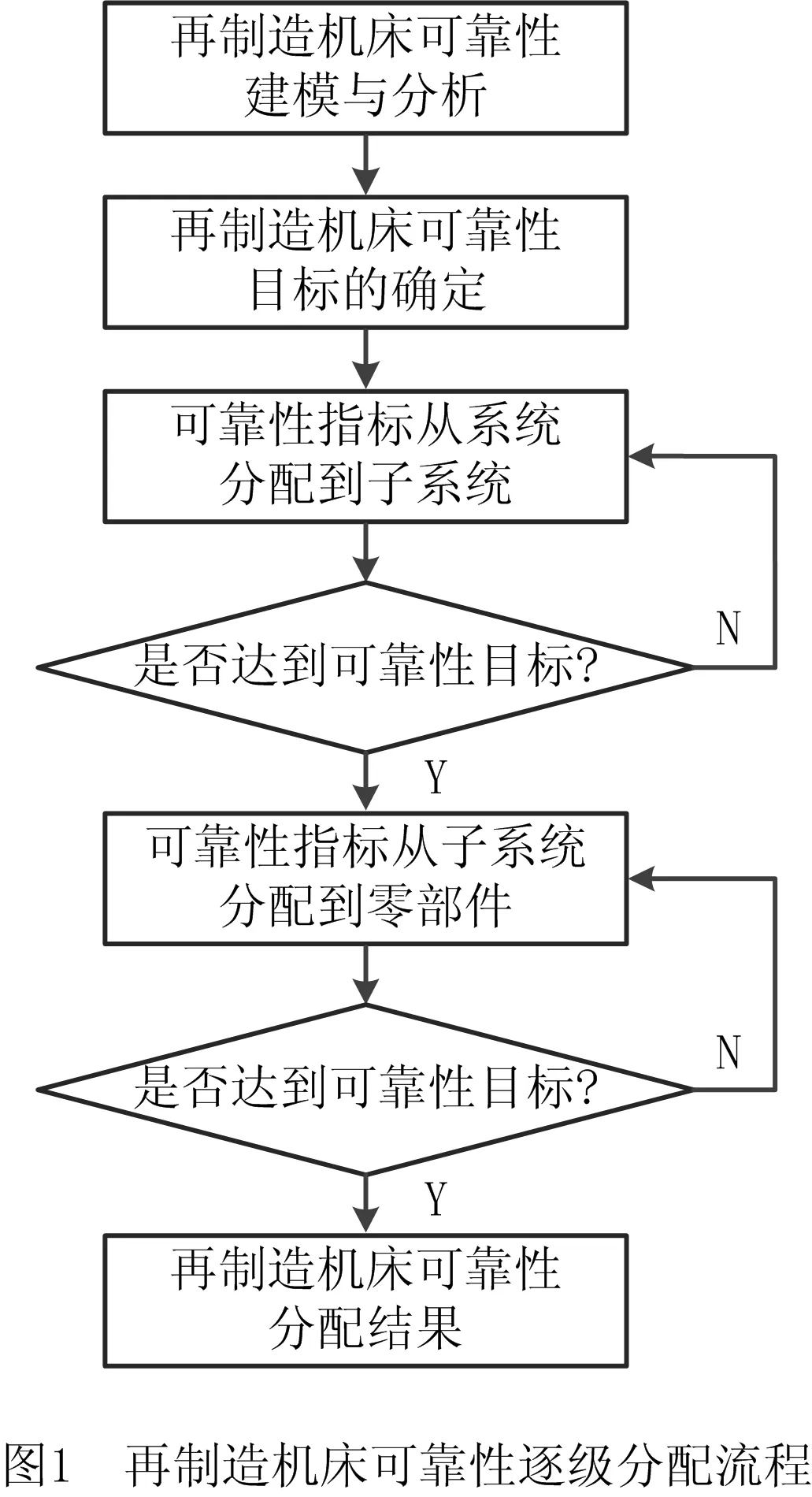
(1)可靠性模型的构建 基于可靠性逐级分配的思想，引入将故障逐级分解的故障树分析，建立再制造机床的可靠性分析模型。再制造机床的故障树模型可以直观地反映系统各零部件之间的功能关系。同时，将各零部件可靠性与系统可靠性间的逻辑关系用数学表达式进行直接描述，便于后续分析计算。

(2)可靠性目标的决策 结合再制造机床可靠性模型，按照客户的要求和企业再制造加工能力，确定再制造机床整机的可靠性目标。

(3)系统级—子系统级的可靠性分配 在系统级分配到子系统级时，利用少量的数据建立神经网络模型，直接得出各子系统的可靠性，有利于缩减成本和设计周期。验证分配结果是否满足系统可靠性要求，若满足，则进行下一级分配；否则，需要重新分配。

(4)子系统级—零部件级的可靠性分配 在子系统级分配到零部件级时，由于不同机床零部件级结构差异较大且服役后不同零部件的寿命区别较大，可采用模糊综合评价方法等完成可靠性分配，可充分利用专家经验考虑到重要零部件的再制造特性，并结合故障树分析中重要度的概念考虑各回收零部件的客观条件。可靠性目标由子系统级分配到零部件级，其结果必须满足系统的可靠性要求。如果不满足，就需要重新分配;否则，可输出可靠性分配结果。

为了简化可靠性分配的数学运算并保证严谨性，本文基于以下假设：不考虑组件之间的相互影响，即各个组件和子系统的故障是相互独立的；每个子系统由不同的零部件组成，即意味着某一零部件不可能存在于不同的子系统中；机床及其零部件的故障服从指数分布。

2 再制造机床可靠性建模与逐级分配方法

2.1 基于故障树的再制造机床可靠性建模与分析

故障树分析是一种图形化演绎方法，它通过自上而下逐级演绎分析，找出导致某一故障事件所有可能的原因，进而采取改进措施[17]。故障树逐级演绎的分析方法与可靠性逐级分配的思想高度契合，故采用故障树模型进行再制造机床可靠性建模与分析。故障树建模与分析的主要过程包括顶事件的确定、故障树模型的构建、定性分析、定量分析和改进提升[18]。

2.1.1 再制造机床故障树模型的建立

再制造机床由主轴系统、进给系统、数控系统等多个子系统构成，且每个子系统又由多个零部件构成。在可靠性分配过程中，根据逐级分配的思想，可将再制造机床整机故障作为故障树的顶事件，各子系统故障作为故障树的中间级事件，各零部件故障作为底事件。由于在设计阶段，可靠性指标只分配到零部件级，对零部件的失效模式不作进一步的探讨。基于以上分析，可以建立如图2所示的再制造机床故障树模型。

2.1.2 再制造机床可靠性分析

由故障树模型可知，再制造机床每个子系统及重要零部件的故障都会导致再制造机床整机的故障，故再制造机床是典型的串联系统。在此基础上，引入重要度分析，在再制造机床的可靠性分配过程中，初始可靠性是已知的，因此用概率重要度来度量由底事件的概率变化引起的顶层事件的概率变化程度[19]。其定义如式(1)所示：

(1)

式中：Ij为第j个故障事件的概率重要度；Fj为第j个故障事件的发生概率；Fs为顶事件的发生概率，表示每个基本事件发生概率的函数，即有n个基本事件，则有Fs=F(F1,F2,…,Fn)。根据串联系统可靠性的特点，再制造机床故障树模型中顶事件的发生概率及各事件的概率重要度可以表示为式(2)和式(3)：

(2)

(3)

其中Ri为第i个零部件的可靠度。

在后续可靠性分配中，根据故障树模型划分出的子系统和零部件，将可靠性目标从再制造机床系统分配到各个子系统，再从子系统分配到各个零部件。此外，各零部件的重要度也将作为可靠性分配过程中重要的参考指标。

2.2 基于神经网络的再制造机床系统级—子系统级可靠性分配

在可靠性目标从系统级分配到子系统级时，考虑到构成同类机床的子系统差异较小，且机床再制造属于新兴产业，投入使用的再制造机床数量较少、可靠性数据缺乏的特点，传统的专家评分法、经验法等没有大量历史数据支撑，主观性过大且成本较高。人工神经网络是处理非线性关系的有力工具，能够建立输入样本和输出样本之间的非线性关系[20-21]。大量研究表明，三层人工神经网络已有较强的映射能力[20]，故本文采用三层人工神经网络，利用收集到的可靠性分配成功的少量历史数据，通过训练将其储存在神经网络中。如图3所示，该模型结构包括输入层、隐含层、输出层三部分，层与层之间通过权系数连接。

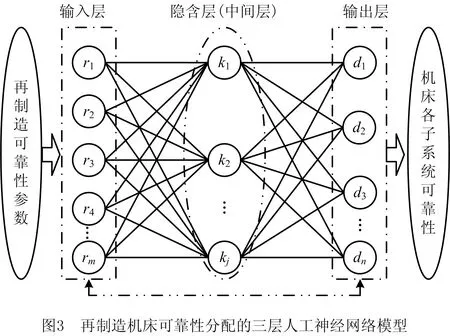
在再制造可靠性分配的三层人工神经网络模型中，将成功分配的历史数据中结构复杂度、重要度等可靠性分配相关参数作为输入X={x1,x2,…,xd}，经过隐含层处理，得到第h个隐含层的输出，如式(4)所示：

(4)

式中：f(·)为隐含层的激活函数；γih为第i个输入层神经元与第h个隐含层神经元之间的权值；d为输入层的神经元个数；λh为阈值。

随后，信号传递到输出层，经过处理后输出层的输出为式(5)：

(5)

式中：f(·)为输出层的激活函数；ωhj为第h个隐含层神经元与第j个输出层神经元之间的权值；m为隐含层的神经元的个数；θj为阈值。

将输出的可靠性结果与实际分配可靠性比较，得到误差函数式(6)：

(6)

式中yj为第j个输出层神经元的期望输出。

若不满足误差精度，则进入误差反向传播阶段。当误差反向传播时，输出误差通过隐含层反向传播到输入层，得到每个元素的误差信号如式(7)所示：

(7)

为了减小误差，结合误差信号修改神经元层间的权值，使权值的调整量与误差的梯度下降成正比，即每次迭代时，权值的变化量如式(8)和式(9)所示：

(8)

(9)

其中η∈(0,1)为学习效率。通过反复迭代可以将误差降低到一个可接受的值，此时输出对应的子系统可靠性分配与优化结果。

2.3 基于再制造因子的再制造机床子系统级—零部件级可靠性分配

2.3.1 基于多层模糊评价的再制造因子量化

依据再制造机床的故障树模型以及可靠性逐级分配的思想，需要将可靠性从子系统级分配到零部件级。由于各个零部件的服役状况、失效形式、寿命状态具有较大的差异性，仅凭少量历史数据不能合理地优化各零部件的可靠性。同时，不同于传统新产品可靠性分配，再制造机床的可靠性分配不仅要考虑产品整体可靠性要求，还需要考虑再制造过程的不确定性对其可靠性分配的影响，如再制造加工技术是否能满足可靠性要求，再制造成本、再制造过程污染排放与各零部件可靠性提升之间的平衡等。因此，有必要建立再制造机床可靠性分配的综合评价体系，通过模糊评价量化再制造过程对可靠性分配的影响，评价结果即为各零部件的再制造因子，其主要反映通过再制造提高该零部件可靠性的可行性。可靠性分配中考虑再制造因子能实现再制造条件与可靠性提升的平衡，获得更合理的可靠性分配结果。如图4所示，再制造机床可靠性分配综合评价体系由技术、成本以及资源环境3个方面的评价指标组成，而每个一级评价指标由多个二级评价指标组成。

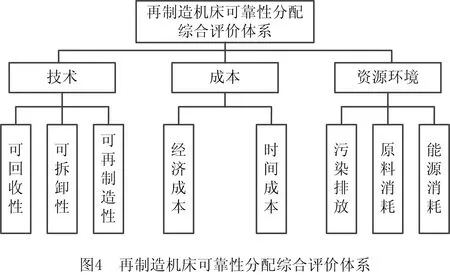
(1)技术指标反映再制造过程的难易程度，包括可回收性、可拆卸性和可再制造性。再制造工艺过程越复杂，分配的可靠性就越低。

(2)成本指标包括机床再制造所花费的经济成本和时间成本。零部件再制造所花费的成本越多，应分配到的可靠性就越低。

(3)资源环境指标反映了再制造过程的环境影响、原材料和能源消耗。对于再制造过程中，提高可靠性对环境污染较大或消耗较多资源的零部件，应分配较低的可靠性。

采用多层模糊评价的方法来量化建立再制造机床可靠性综合评价体系。首先确定模糊评价的对象集Xi={x1,x2,…,xn}，其表示组成第i个子系统的所有零部件。接下来确定模糊评价的因素集，根据再制造机床可靠性综合评价体系建立多级模糊评价因素集U={U1,U2,U3}，其中U1，U2，U3分别为一级评价指标，有U1={u11,u12,u13}，U2={u21,u22}，U3={u31,u32,u33}。然后建立评价集V={V1,V2,…,Vl}，因评价体系是确定再制造过程各指标对可靠性分配的影响程度，故评价集为V={大,较大,一般,较小,小}。专家需要考虑再制造过程的影响，并对每个部件进行评分，具体的评分规则如表1所示。

表1 各指标的具体评分标注

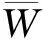
(10)

(11)

(12)

每个零部件的综合评价指标：

Aij=W°Bij。

(13)

最终再制造因子即量化再制造对可靠性分配影响的评价指标结果为：

σij=Aij·VT。

(14)

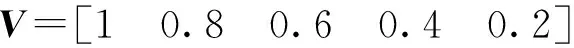
通过再制造评价体系得到的再制造因子考虑了再制造过程中各因素对可靠性分配的影响，反映了再制造的特点，这是再制造机床可靠性分配与传统机床可靠性分配的主要区别。

2.3.2 再制造因子与概率重要度结合的可靠性分配方法

根据故障树分析中的重要度分析等相关理论，概率重要度反映了低层事件的可靠性变化对高层事件概率的影响。在可靠性分配中引入概率重要度，优先考虑提高重要度较大的零部件的可靠性，能更有效地提高再制造机床整机的可靠性。将再制造因子与重要度结合，得到如式(15)所示的综合因子：

(15)

式中Fij、Iij分别表示第i个子系统中第j个零部件的故障概率及概率重要度。故障发生概率越大，可靠性提升的潜力越大；概率重要度越高，分配的可靠性越高；而再制造因子反映了再制造实施的难度，其值越高，需要分配的可靠性越低。

对第i个子系统，按照综合因子的比例分配其零部件的可靠性，如式(16)所示：

Δri1:Δri2:…:Δrin=ki1:ki2:…:kin。

(16)

式中Δrij为第j个零部件可靠性的变化值。

最后，调整后的子系统可靠性应满足系统要求的可靠性目标，则有约束式(17)：

f[(ri1+Δri1),(ri2+Δri2),…,

(17)

联立求解式(15)～式(17)，可将再制造机床的可靠性指标从子系统级分配到零部件级，同时保障各子系统能满足可靠性目标。

3 工程算例分析

数控滚齿机是齿轮加工中重要的加工设备，广泛应用于齿轮加工行业。现有某齿轮制造厂需要对大量服役已久的数控滚齿机进行再制造。根据客户的要求，该再制造数控滚齿机设计阶段的可靠性目标设定为R*(500)=0.65，即再制造数控滚齿机的平均故障间隔时间约为MTBF=1 160.68 h。

分析数控滚齿机床结构，将其分为几个子系统，每个子系统由不同的零部件构成。考虑到某些子系统或零部件的加工技术已相对成熟、可靠性高，且其对再制造数控滚齿机可靠性影响较小，为了简化计算，本文暂不考虑这部分子系统或零部件的可靠性分配。根据结构分析，确定再制造数控滚齿机的各子系统级零部件构成情况如表2所示[22]。

表2 再制造数控滚齿机的各子系统级零部件构成情况

续表2

各零部件初始可靠性已知，根据式(2)和式(3)可以求出各子系统的初始可靠性及其零部件的概率重要度，如表3所示。

表3 各子系统及零部件的初始可靠性及概率重要度

3.1 可靠性指标分配至子系统级

采用三层前馈神经网络将再制造数控滚齿机系统的可靠性目标分配至各子系统。神经网络的部分训练样本如表4所示。

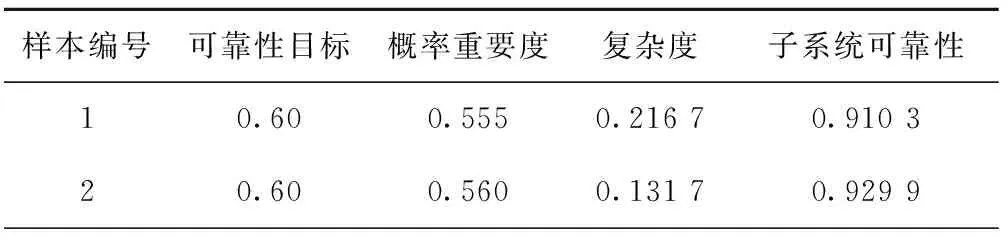
表4 三层前馈神经网络的部分训练样本

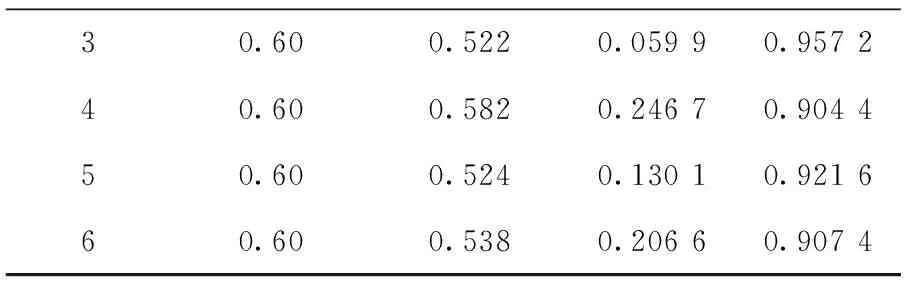
续表4

其中，可靠性目标指的是整机可靠性目标，此处取值0.60为某训练样本的可靠性目标值；复杂度是指组成子系统的零部件数量占整机零部件数量的比例。参考80%训练样本和20%测试样本的比例，用50个样本训练该神经网络模型。结合三层神经网络的结构要求，构建输入层3个节点，隐含层9个节点，输出层1个节点的前馈神经网络。经过多次试验确定网络的学习效率为0.1，动量因子为0.2，迭代10000次后，误差收敛效果如图5所示。达到精度要求后，将数控滚齿机的可靠性分配参数输入到该模型中，可得到6个子系统的可靠性分配结果，如表5所示。

表5 各子系统的可靠性分配结果

3.2 可靠性指标分配至零部件级

在可靠性指标分配至零部件级时，先邀请部门领导和专家分别按照综合评价体系和表1中的评分规则对再制造机床各零部件评价打分。然后，根据式(15)～式(17)对各部分进行可靠性分配。以刀架组件子系统为例，邀请了5位专家对各零部件进行评价，其中对主轴的评分如表6所示。

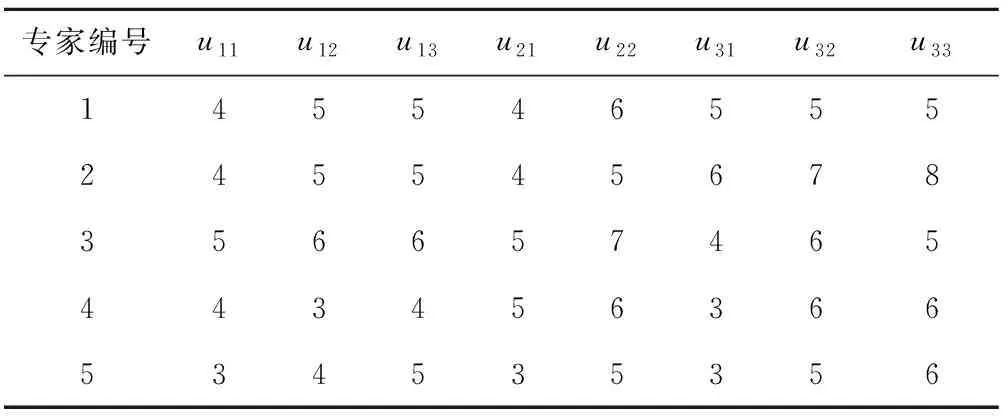
表6 主轴再制造的专家评分结果

根据专家的评分结果，可得主轴的评价矩阵为：

(18)

三个一级评价指标的权重为W0={0.45,0.4,0.15}。由于二级评价指标的权重按平均原则分配，故最终每个指标的权重为W：

W=[0.15 0.15 0.15 0.2 0.2 0.05 0.05 0.05]。

(19)

根据式(13)计算主轴综合评价指标，结果如式(20)所示：

(20)

结合式(14)，主轴的再制造因子为0.01×1+0.24×0.8+0.55×0.6+0.2×0.4+0×0.2=0.612。同理可得锥齿轮1和轴瓦的再制造因子，基于再制造因子结合概率重要度对刀架组件的各零部件进行可靠性分配，结果如表7所示。

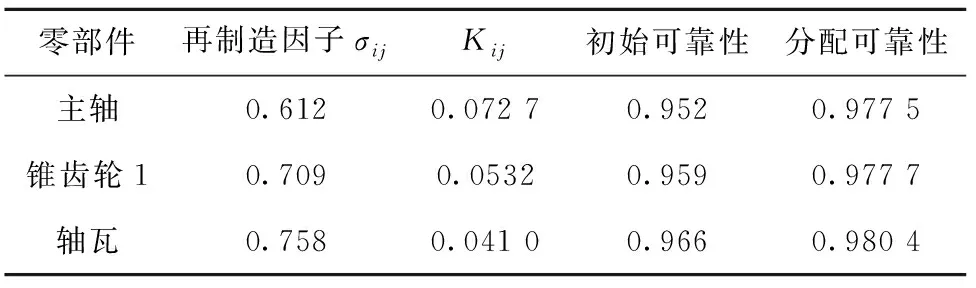
表7 刀架组件各零部件的可靠性分配结果

表8 各零部件的可靠性分配结果

3.3 结果分析

再制造机床作为一个系统，其可靠性直接受到各个零部件的影响。然而，由于再制造过程的不确定性，加上提高各零部件可靠性的难度不同，使得再制造机床可靠性分配与传统新机床可靠性分配有很大不同。再制造机床的可靠性分配需要综合考虑每个零部件的可靠性水平，以及可靠性提升对再制造技术、成本与资源的要求，达到各零部件可靠性目标与现有资源的平衡，从系统的角度来实现对再制造机床的可靠性优化。

实例表明，该方法可将再制造机床的可靠性目标分配到各组成零部件，并能达到指定的可靠性目标。如图6所示为再制造机床各零部件件可靠性分配前后对比。工程算例的分析结果表明，各零部件及子系统的可靠性均有了显著提升，再制造机床整机可靠性从0.508提高到0.657。此处仅仅是算例的运行结果，可为再制造设计提供可靠性数据方面的支撑与指导，而实际可靠性提升的结果受到再制造过程实际情况以及新采购零部件可靠性数据的影响。

4 结束语

本文提出了再制造机床可靠性逐级分配的思想及基于神经网络和再制造因子的再制造机床可靠性分配方法。

(1)再制造机床由主轴系统、刀架系统、传动系统、数控系统等多个子系统构成，而各个子系统又包含多个零部件。为此，考虑各个子系统及零部件之间的区别及联系，按照逐级分配的方法，将再制造机床可靠性分配划分为两个阶段：系统级—子系统级、子系统级—零部件级。

(2)在将整机系统可靠性分配到子系统级时，利用少量历史数据训练了再制造机床可靠性分配的神经网络模型；在可靠性从子系统分配至各零部件时，引入再制造因子，其综合考虑了每个零部件的损伤情况及提高可靠性对再制造技术、成本与资源的要求，并与重要度的概念结合，实现再制造机床各零部件的可靠性分配。

(3)工程算例分析表明，根据本文所提出的方法，再制造数控滚齿的可靠性得到合理的分配，整机平均故障间隔时间从738 h提高到1 190 h(仅为算例结果，实际结果受到再制造过程及零部件供应商的影响)，可以满足系统可靠性目标。

目前，再制造装备可靠性分配方面的研究较少，再制造可靠性分配需要考虑的因素较多，研究空间很大。本文所提方法为再制造机床的可靠性分配提供了一种合理的解决方案，对设计阶段再制造产品的可靠性分配具有重要的参考价值。随着研究的深入和再制造产业的发展，所提方法还有进一步提升的空间。为了提高可靠性分配的准确性，采用神经网络进行可靠性分配需要获得更多的可靠性数据来修正结果，但再制造作为一个新兴产业，难以获取大量可靠性数据。此外，结合不同的企业以及不同的装备，可靠性的提升需要考虑的影响因素不同，再制造综合评价指标体系还应该不断丰富完善。从机床再制造全过程管理的角度出发，制造商应考虑机床在服役过程中的可靠性变化，利用先进的物联网技术、云储存平台等，建立机床运行监控系统和大数据管理系统。