高温应力工况下汽车继电器触点失效机理的研究＊

王燕兵 ， 赖雅丽

（贵州电子信息职业技术学院，贵州 凯里 556000）

继电器广泛应用于大电流电器控制系统中，据统计触点部分的故障率占到继电器故障率的90%以上[1-2]。热设计是密封继电器中触点接触参数优化设计的关键参数，稳定的接触条件是降低触点接触面产热导致熔焊故障的关键，触点吸和分断进程中应尽量减少接触面间产热，使触点表面材料熔焊降低。本文基于传热理论建立了触点电热耦合作用的数学模型，着重分析继电器触点传热特性及温度场分布的影响规律，揭示汽车继电器触点瞬态接触传热特性，对改善继电器触点熔焊故障具有重要的现实意义，为触点间工艺改进提供理论支撑。

1 继电器触点电热耦合数学模型

继电器触点吸和传导大电流工作时，继电器触点传热特性受材料性能、触点间的接触电阻、接触行为等因素的影响。本文在深入分析触点间的界面接触电阻数学模型的基础上，利用非线性瞬态热传导理论进一步探究触点间的电热耦合作用。图1所示为继电器触点间接触行为示意图。为了建立吸和分断过程电热耦合模型明晰触点间传热机制，作如下假设：1）触点材料各向同性；2）忽略材料的氧化烧蚀作用；3）忽略触点本体电阻生热。

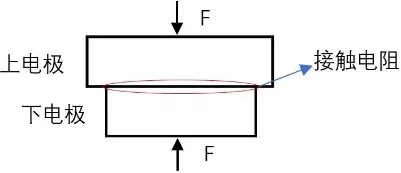
图1 继电器触点间接触

利用焊接热源的非线性瞬态热传数学模型描述继电器触点间传热，其方程为：

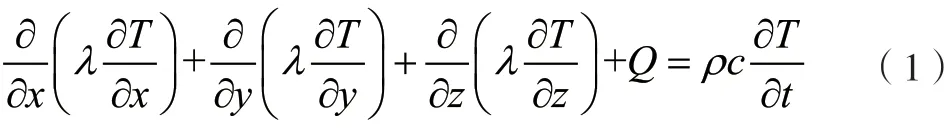
式中：Q-热源；λ-导热系数，w/(m·℃)；ρ-密度，kg/m3；c-比热，J/(kg·℃)。

触点间接触形成的热源Q，可由式（2）计算：

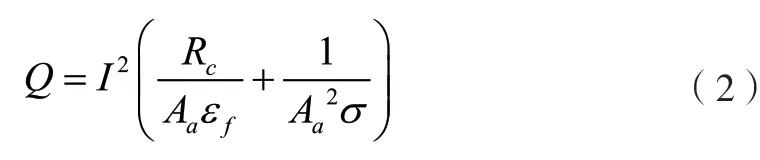
式中：I-电流，A；Rc-接触电阻，Ω；Aa-触点间接触面积，m2；εf-触点间接触间隙，m；σ-电导率，Ω-1·m-1。

采用Hertz理论对触点间接触面积计算，见式(3)：

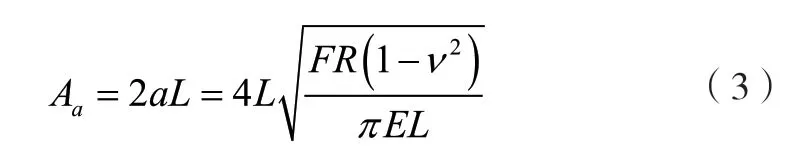
式中：F-电极夹持力N；R-半径，m；ν-泊松比；E-弹性模量MPa；L-触点间接触长度，m。

由于上述建模过程中，部分相关参数需要通过实验测量获得，导致模型数值计算存在困难。为此，本文利用模拟仿真和实验验证的方法，对分断过程中触点间的传热及温度场分布规律进行分析研究。

2 仿真实验与分析

针对继电器触点间接触的电-热-力耦合，选用传热模块中的焦耳热、固体传热和结构力学中的固体力学，建立瞬态接触耦合过程，在COMSOL 模型向导中新建一个关于继电器触点间接触传热的三维空间维度分析，分别选择传热物理场下的固体传热模块、焦耳热模块和结构力学物理场下的固体力学模块。选用瞬态研究，完成对接触模型仿真环境的基本设置。

2.1 有限元模型的建立及边界设置

本文采用COMSOL有限元软件对触点间分断进程中的电热耦合作用进行分析计算。触点间采用细分网格的方法对接触区域进行重点分析，采用表面阻抗的方法对接触电阻进行设置。模型中，继电器触点尺寸根据实际参数设计，仿真计算选用材料的主要物理参数，如热扩散系数、比热、导热系数等，具体数据参见文献[3]。本文在 COMSOL 接触对特征设置窗口中选择罚函数法作为计算方法，对继电器触点接触表面分别添加接触对，如图2所示

图2 接触对设置

2.2 仿真结果分析

继电器触点电场分布是耦合了导电和材料变形的复杂非线性过程，且根据文献[4]吸和分断时间仅为10μs、瞬时性强，触点材料的相关物理性能参数均为随温度变化的特点，单纯依靠理论计算或试验的方法很难对继电器触点熔焊现象进行全面深入的分析研究。本文采用COMSOL有限元计算方法综合考虑如材料的热物理性随温度变化、接触电阻随温度变化及多物理场耦合等对触点电场分布的影响。

图3 为横截面电荷密度分布，图4为横截面电流密度分布。由仿真结果可知：电流密度沿接触截面径向的分布并不是一个固定值，也就是说是非均匀分布，整体呈现由中心向边缘逐渐递增的趋势，而且在接触的外边缘区域相对较大，形成环状较高电流密度分布，进而导致焦耳热也就是环形热源。

如图5、图6所示，由仿真结果可知：接触初始时接触面外温升影响不大；在接触面间短时间内由于接触电阻在电流的作用下产生的焦耳热不断温升；接触区域温升与空间电荷密度分布云图一致，同时由于接触面间接触热阻的存在导致热量聚集在接触面之间，进而导致触头接触面间材料达到熔点产生熔焊故障。

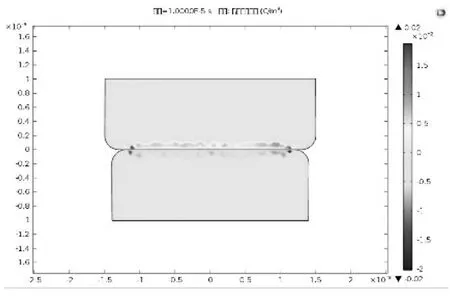
图3 横截面电荷密度分布

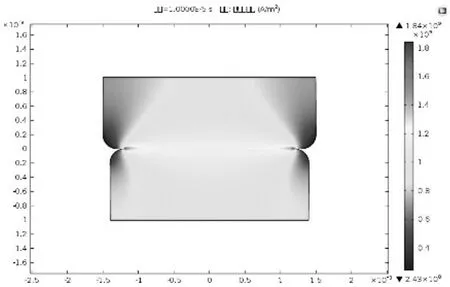
图4 横截面电流密度分布

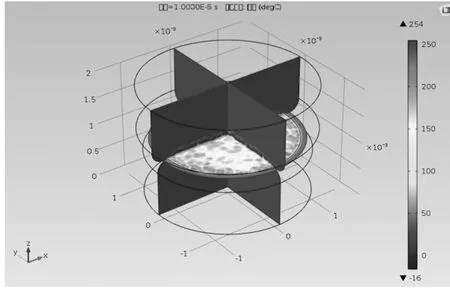
图5 触点1μs时温度分布

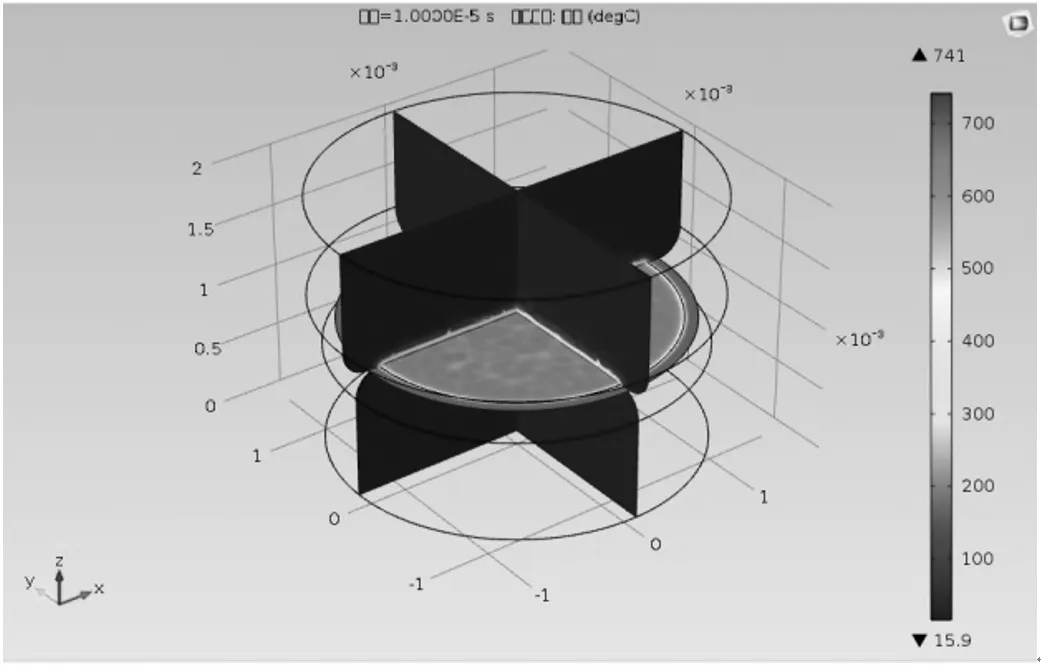
图6 触点10μs时温度分布

3 结论

本文在综合分析触点间接触电阻形成机理的基础上，提出触点分断进程中瞬态热场的机-电-热-固间耦合分析仿真方法，建立了触点间分断进程中接触电阻产热瞬态热场数值模型。对工况电压12V下触点间热场分布进行模拟求解，得到了接触面间接触电阻产热的接触面温度场分布，探究了接触电阻在电流作用下产生的焦耳热是导致触头间金属熔化的主要原因，为改善继电器触头熔焊现象提供理论支撑。