基于改进布谷鸟算法的电力系统优化调度
2021-05-07谭卓然
谭卓然
(三峡大学 电气与新能源学院,湖北宜昌 443000)
引言
随着我国用电量的不断增加,电力系统的安全稳定运行成为了电力工业关注的热点问题。因此,对电力系统进行优化调度是关键问题。
截至目前,已有诸多学者对电力系统的优化调度进行了研究[1-5],但目前的算法均存在一定的明显缺陷,如计算速度慢、计算精度相对模糊等。
本研究对原有布谷鸟算法加以改进和优化,运用该改进算法对建立的调度模型进行优化,验证了该改进算法的优越性。
1 改进型布谷鸟算法
1.1 布谷鸟算法
布谷鸟算法结合了常见的布谷鸟传播机制和征费搜索方法[6]。该算法在一开始时的搜索能力比较好,但随着时间的推移,其搜索能力的缺陷逐渐暴露,同时存在的问题还包括搜索精度低、速度慢等,在解决多目标问题时有必要进行改进。针对一个d维的优化问题,就需要d个变量:

基于莱维飞的位置更新公式为:

1.2 改进型布谷鸟算法
改进型布谷鸟算法流程图如图1所示。

图1 优化流程图
2 优化调度模型
电力系统的最优调度是建立在系统的供电量和需求负荷之间平衡的基础上,既要满足系统最小发电成本,又要使污染气体的排放量符合标准。
(1)经济调度目标:
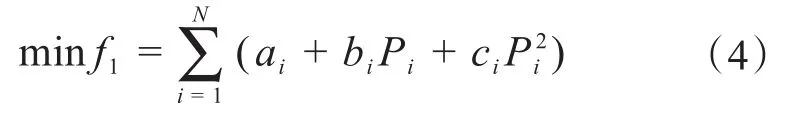
式中:N表示火电机组数量;ai、bi、ci分别是机组的发电成本系数;Pi是机组出力;f1表示经济调度的目标函数。
(2)环境处理目标:

式中:αi、βi、γi、ξi分别是污染物的排放系数;f2表示环境调度目标函数。
将两个目标函数和约束条件联立得到以下多目标优化调度的模型:
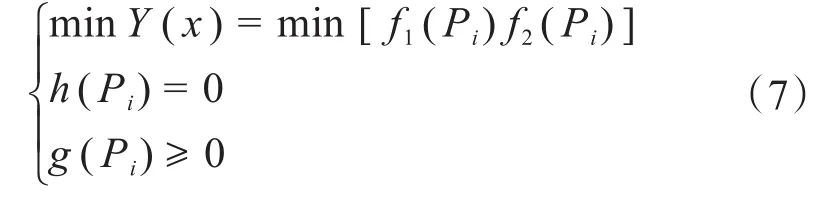
式中:h(Pi),g(Pi)分别为调度模型的等式和不等式约束条件;Y(x)为整合后的目标函数。
3 算例分析
选择IEEE6单元的30节点的系统。采用不同算法对模型进行分析和比较,以24 h为周期进行计算,单位运行的参数、发射系数和线路功率损耗见文献[7],单位G1-G6输出的上限和下限以及系统需求负载见文献[8]。
保持参数条件一定,分别采用MOPOS算法、NSGA算法和多目标布谷鸟算法及其改进算法对以上算例进一步分析,设种群大小为N=200,迭代次数的最大值为T=600,执行交流的门限值为0.6,迭代过程如图2、3所示。

图2 发电成本变化

图3 污染排放变化
从图2和图3的迭代曲线可以看出,与其他算法相比,改进后的布谷鸟算法,其迭代次数呈现很大幅度的减少,关键是因为引入了AC算子、动态参数和非控制性排序,导致算法在搜索效率方面和收敛速度方面产生变化。其中,NSGA算法进入收敛状态需80次迭代,MOPOS算法、多目标布谷鸟算法及其改进算法分别以72、61和48次迭代进入收敛状态。改进的布谷鸟算法提高了收敛速度和优化能力。
迭代完成后,通过NSGA算法、MOPOS算法、多目标布谷鸟算法和改进的多目标布谷鸟算法获得的最优Pareto边界如图4~7所示。表1显示了通过不同算法优化调度模型后的单位输出和目标函数的结果,其中PGi(i-1~6)是单位输出。

图4 NSGA最优前沿

图5 MOPOS最优前沿

图6 布谷鸟算法最优前沿
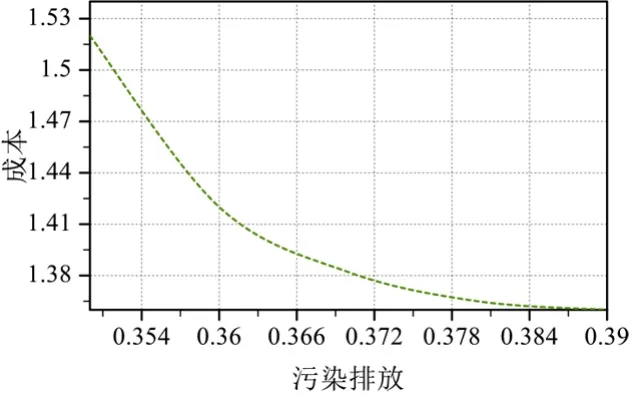
图7 改进算法最优前沿
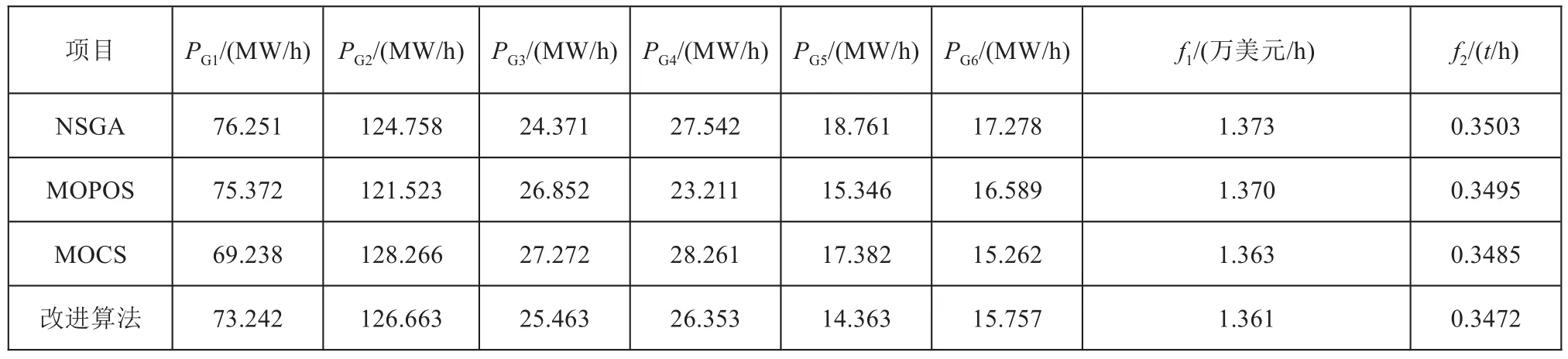
表1 优化结果
从图4到图7可以看出,当区域电网的需求负荷确定时,发电成本与污染物排放呈反比,两者之间相互制衡。经比较可以看出,前三种算法没有搜索得到最优的帕累托峰,图4~5早期获得的最优帕累托峰的斜率过大。而后期的算法又太小,图6中段的斜率有一定程度的波动,后期的算法是间歇性的,而改进后的算法可以得到平滑、积分的最优Pa‐reto前沿。从表1可以看出,该算法的发电成本和污染物排放分别为1.361万美元/h和0.3472 t/h。与其他三种传统算法的优化结果相比,降低了发电成本和污染物排放。由此可见,解决多目标优化问题上改进后的算法拥有较好的效果。
4 结论
改进算法的计算精度更高,同时能有效提高全局收敛性以及保证Pareto非劣解的多样性。
