Generation of non-integer high-order harmonics and significant enhancement of harmonic intensity∗

Chang-Long Xia(夏昌龙), Yue-Yue Lan(兰悦跃), and Xiang-Yang Miao(苗向阳),†

1College of Physics and Information Engineering,Shanxi Normal University,Linfen 041004,China

2Key Laboratory of Spectral Measurement and Analysis of Shanxi Province,Shanxi Normal University,Linfen 041004,China

Keywords: non-integer high-order harmonic generation, the orthogonally two-color laser field, the enhancement of harmonic intensity

1. Introduction

Interaction between strong laser fields and atomic or molecular systems has become a hot topic with the development of high intensity ultrashort laser pulsed lasers. The nonlinear coupling of a strong laser field with a target can produce many new phenomena such as high-order harmonic generation(HHG),[1–7]above-threshold ionization(ATI),[8]nonsequential double ionization,[9]and Coulomb explosion.[10]Exploration of these new phenomena has promoted research progress in strong field physics.

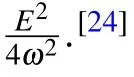
Both odd and even harmonics could be obtained by breaking the symmetry of the system,such as using two-color field or multi-color field,[30–33]adding chirped field,[34]employing inhomogeneous field[35]to break the symmetry of the laser field, or using complex molecular systems to break the symmetry of the target.[36]The appearance of 3n±1 order harmonic pairs is achieved by the action of targets and twocolor counter-rotating circularly polarized laser fields.[37–39]Selection rules for atomic and molecular systems under the N-fold symmetries field radiation were also explored.[40]Recently,only even order harmonics were discussed in the polar molecule CO,[41]nonpolar molecular N2[42]and symmetrical ion system H+2by adding a static filed.[43]The common point of pure even harmonic research is that in the case of asymmetric electronic motion of the molecular axis, adding linearly polarized laser field in its vertical direction will cause pure even harmonics in the molecular axis direction and pure odd harmonics in the laser direction. In addition, Neufield et al.used the Floquet group theory to deduce the selection rules for HHG and its polarization in targets for driving laser field with various temporal and spatial symmetries in 2019.[44]

In either odd or even harmonics,the high-order harmonics are radiated with the integer order of the incident pulse.However,non-integer order high-order harmonics or pure even harmonics from rare gases have not been reported to our best knowledge. In this work, we propose a solution to achieve the simultaneous generation of non-integer pure-even-order harmonics by numerical simulation in the helium atom. The harmonic intensity in the orthogonally two-color(OTC)laser field is improved by three orders of magnitude compared to the monochromatic field with the same intensity. The physical mechanism for the generation of pure even order harmonics is explained from the characteristics of the dipole acceleration,which is a method different from the Floquet group theory in Ref. [44]. Compared with molecular systems, we provide a simple and easy method for experimentally achieving the separation of odd and even harmonics.It should be noticed that the generation of non-integer orders provides theoretical guidance for experimentally filtering out harmonics of finer frequency multiples,which can achieve the purpose of improving energy resolution.

2. Theory and method

Time-dependent wave function can be obtained by numerically solving the Schr¨odinger equation under the length gauge(atomic units are used unless stated otherwise)

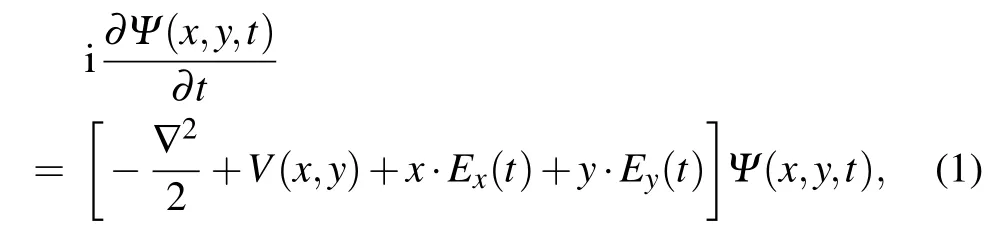
where the two-dimensional model potential of the helium atom is set to

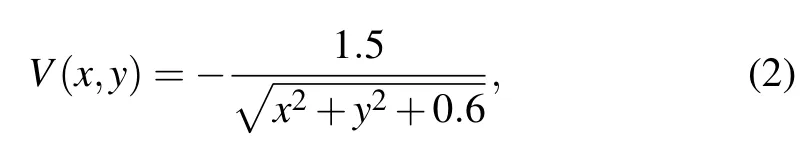
which corresponds to the binding energy of 0.9 a.u. for the ground state of a helium atom.The OTC laser pulses scheme is used in the simulation, which combines a linearly fundamental field with frequency ω1in the x component by combining a weak field with frequency ω2in the y component. The laser field in two components can be written as

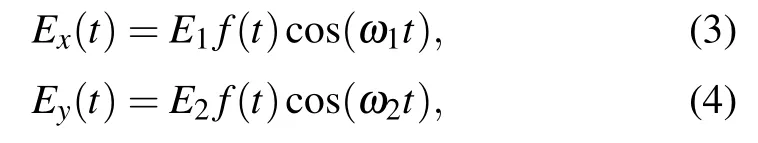
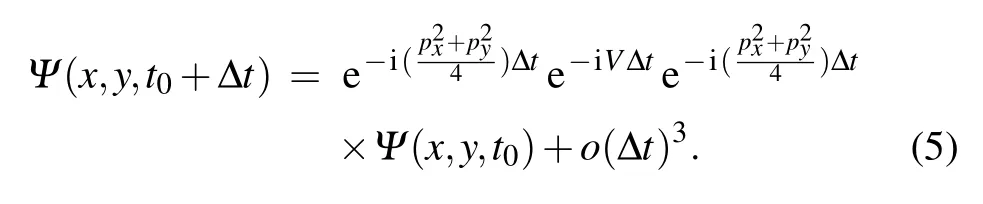
The dipole acceleration of the x and y components is derived from the Ehrenfest theorem

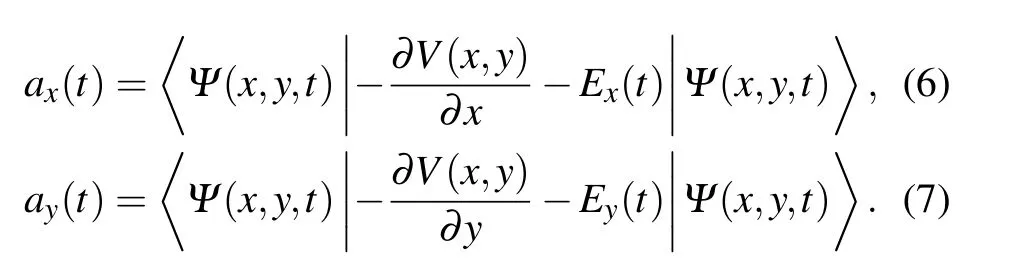
The harmonic spectrum on the two components is obtained from the absolute square of the Fourier transform of the associated dipole acceleration,respectively,

3. Results and discussion

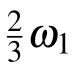
Fig.1. High-order harmonic spectra from the OTC laser field. In the calculation,ω1=0.057 and ω2=are used,which are corresponding to λ1 =800 nm and λ2 =1200 nm. The thin black line and the thick red line represent the high-order harmonics radiated in the x and y directions,respectively.

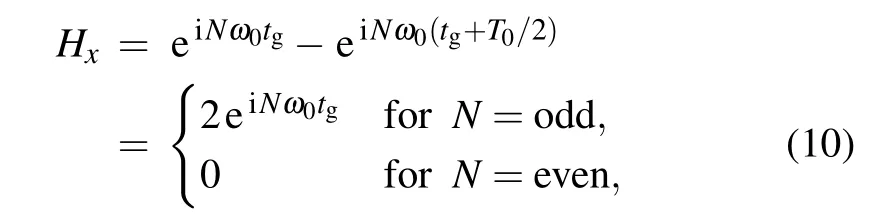
which is exactly the reason why the atomic system generates only odd order harmonics in a monochromatic field. However,it is very different for the y direction. As shown in Fig.2(c),the signs of dipole acceleration at tgand tg+T0/2 are the same,leading to the same sign of the high-order harmonics radiated in consecutive half cycles. Therefore,the interference in y direction is

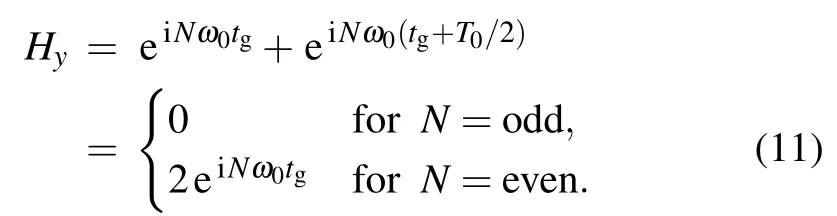
In a word, in the OTC scheme, the harmonic emission order is neither an integer multiple of ω1nor an integer multiple of ω2,but an integer multiple of the frequency of the synthesized total electric field. In the case of ω1:ω2=3:2,only odd and even orders harmonics of ω0are radiated in the x and y directions, respectively, which can be explained by Eqs. (10) and(11). Those discussions give an idea to separate pure odd and pure even order harmonics in experiment. Other parameters of the laser field are simulated for further investigation.

Fig.2. (a)The evolution of Ex,Ey with period of T0 over time. (b)and(c)The time-dependent dipole acceleration in x and y directions,respectively. The plus sign+indicates that harmonics have positive phase and the minus sign −indicates that harmonics have negative phase. Two dot-dashed olive lines represent two arbitrary moments that differ by half an optical cycle of T0. (d)The Lissajous figure of OTC combined laser field. Black solid arrow and red hollow arrow indicate the direction of evolution of the laser field.

At different ratios of frequencies,the local high-order harmonic spectra of the plateau in two components is displayed in Figs.3(a)–3(d)to show the phenomenon more clearly. The frequency of two incident pulses in Fig.3(a) is ω1= 3ω0,ω2=4ω0,and the harmonic order is similar to that in Fig.1.The harmonics generated in the x direction are odd multiple of ω0,and in the y direction are even multiple of ω0.Figures 3(b)and 3(c) repeatedly show us the harmonic spectra with frequency ratio ω1=3ω0, ω2=6ω0and ω1=3ω0, ω2=9ω0,and the harmonic orders in both figures are found to be integer multiples of ω1. This is because the period of the synthesized pulse is the same as the period of the laser field pulse in the x direction, i.e., ω0=ω1. In Fig.3(b), there are only even orders in the y direction, while in Fig.3(c), there are only odd orders. This is due to the symmetry of the Lissajous figure of the synthesized total laser pulse.

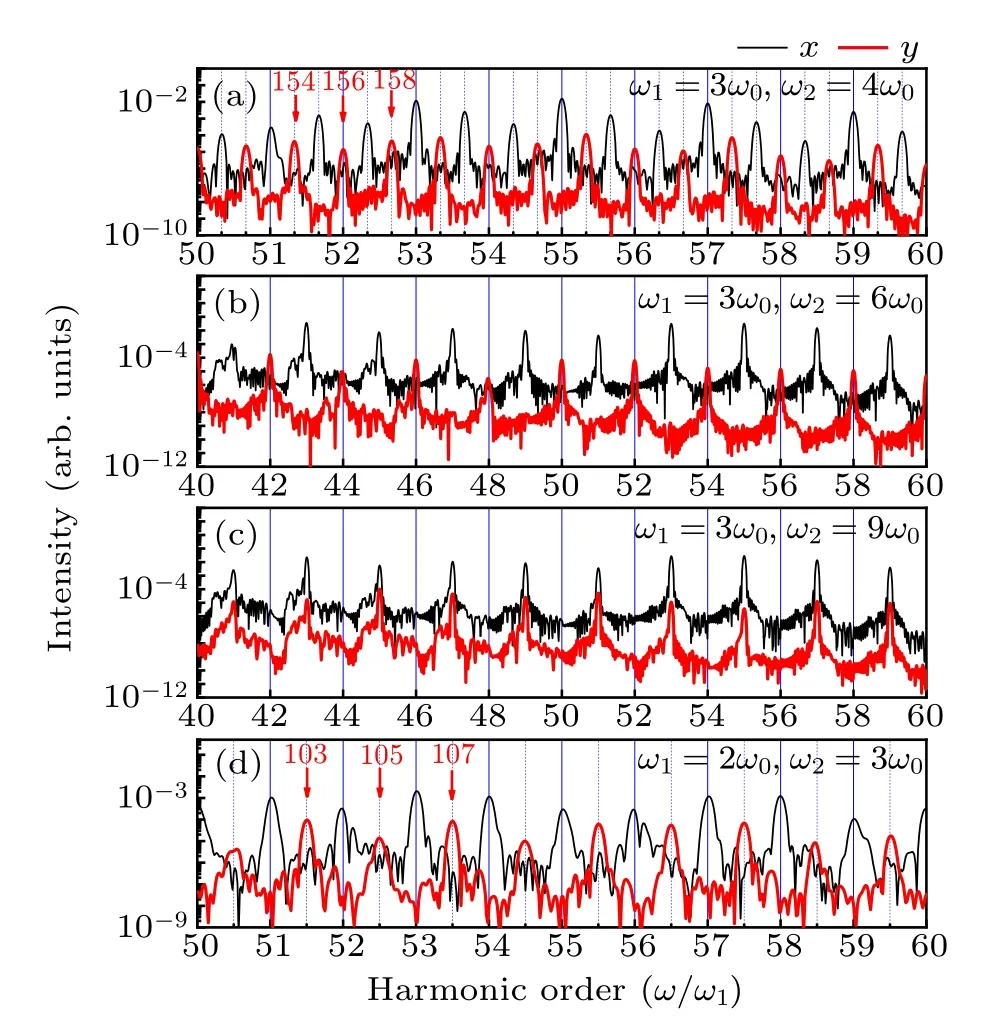
Fig.3. (a)–(d)Harmonic spectra of helium atom at different frequency ratios of the incident laser field in x and y directions, which are represented by thin black and thick red lines,respectively.

We also simulate the case of ω1= 2ω0, ω2= 3ω0, as shown in Fig.3(d). The results show that pure even order harmonics of ω0are generated in the x direction, and their strength is stronger than pure odd order harmonics of ω0in the y direction. Compare with Fig.1,the parameters in Fig.3 are equivalent to exchanging the intensities of two lasers,and there still exists the phenomenon that pure odd and pure even order harmonics are separated in two directions. We also simulate other intensity ratios and find that the intensity ratio in the OTC scheme has an influence on the harmonic intensity in two directions but the selection of harmonic orders are impervious.

Through the above analysis, a scheme to separate pure odd and pure even harmonics is obtained. If the frequency of two laser pulses is not a integer multiple,the obtained harmonic order is related to the frequency ω0of the synthesized total laser field. This shows that although the frequencies ω1,ω2of the incident pulses are relative high,harmonics of the order ω0with better resolution can be generated. This provides a good idea for obtaining harmonics with finer orders.

Fig.4. (a)The total harmonic spectra when the frequency of two incident pulses are ω1=ω0,ω2=3ω0 and ω1=3ω0,ω2=ω0,which are represented by thin red and thick blue lines, respectively. (b) The total harmonic spectra generated by a monochromatic field with a intensity of 3.12×1014 W/cm2 and a wavelength of 1600 nm. (c)The laser field evolution of two-color laser field from parallel polarization over time. (d)High-order harmonic spectra radiating from parallel polarization two-color pulse. The inset is an enlarged view of the harmonic spectra of order 40th to 60th.

In addition, the widely discussed two-color field scheme that two incident lasers are superimposed on the same polarization direction is also simulated, while keeping other laser parameters consistent with the thin red line in Fig.4(a). It can be seen from Fig.4(d) that the harmonic intensity of the total harmonic is higher than the monochromatic laser field intensity in Fig.4(b), which is close to the harmonic intensity of red line in Fig.4(a). From the evolution of the laser field over time,the direction of the laser field is reversed every half cycle, but the amplitude is different, thus both even and odd harmonics appear in the inset of Fig.4(d). It can be seen that the two-color field superposition of the same polarization direction cannot separate pure odd and pure even harmonics. To sum up,if you want to have a scheme that can get high intensity harmonics with fine resolution and can separate pure odd and pure even harmonics, then the OTC scheme is the best choice.

4. Conclusion

In summary, we have investigated the interaction of helium atom with orthogonally two-color (OTC) laser field by solving the time-dependent Schr¨odinger equation. When a combined field of ω1:ω2=3:2 is used, the generated harmonic orders are neither integer multiples of ω1nor integer multiples of ω2, but are generated at integer multiples of the synthesized total laser field frequency ω0. The harmonic spectra present the rules of the pure odd orders in the x direction and the pure even orders in the y direction due to the symmetrical features of Lissajous figures. Then the radiation mechanism of pure even order harmonics is explained using the evolution of laser field and the time-dependent change of dipole acceleration. Compared with the monochromatic laser field of the same total intensity,the OTC laser field has the advantage of significantly improving the harmonic intensity. The conclusion is verified by changing the frequency ratio of the laser field. We propose not only a scheme to achieve the separation of pure odd and pure even order harmonics in atoms,but also a scheme to improve energy resolution, and at the same time provide a simple and effective scheme for significantly improving harmonic intensity. It provides theoretical guidance for the development of atom high-order harmonics in experiments.