Efficient self-testing system for quantum computations based on permutations*

Shuquan Ma(马树泉), Changhua Zhu(朱畅华),2,†, Min Nie(聂敏), and Dongxiao Quan(权东晓)

1State Key Laboratory of Integrated Services Networks,Xidian University,Xi’an 710071,China

2Shaanxi Key Laboratory of Information Communication Network and Security,Xi’an University of Posts&Telecommunications,Xi’an 710121,China

3School of Communications and Information Engineering,Xi’an University of Posts&Telecommunications,Xi’an 710121,China

Keywords: quantum computation,verification,self-testing systems,complexity theory

1. Introduction

It is generally believed that quantum computers can accelerate the solving of some difficult problems that are thought to be intractable on classical computers.[1,2]Nowadays,many experimental implementations of quantum computation have been demonstrated.[3–7]In late 2019, Google Inc. shocked the quantum computing community by announcing that their quantum computer achieved the quantum supremacy.[8]This is the watershed where the quantum computer surpasses the classical computer in processing some specially practical issues. In spite of this declaration aroused a continuing controversy, it brings us an inevitable question: If a problem can not be efficiently solved by a classical computer,how can one believe that the solution obtained by a quantum computer is exactly correct? Indeed,this question has been investigated in complexity theory for many years.[9]However, as far as we know,almost all existing works only concern interactive proof(IP)systems[10](see Ref.[9]). Informally speaking,an interactive proof system traditionally is modeled as a two-party interactive game where two players,an all-powerful prover and a capacity-limited verifier, interact with each other in a backand-forth way. At the end of the game,the verifier accepts or rejects the output of the prover,i.e.,the computation outcome.In this paper, we take a different perspective to analyze this question for the first time by introducing the concept of selftesting systems into the complexity class. Simply speaking,we say a problem has a self-testing system if the computing machine can verify the correctness of the computation by itself according to a part of the computation output. In another word,a self-testing system is a computing machine such that it takes a problem as the input,then after finite steps,outputs the solution of the problem together with a message which can be used to verify if the computation is performed correctly. One may argue that whether it is necessary to define such a model.We give a few reasons to make this point more substantial.

First, the IP system only suits the scenario where a client and a server, probably in distance, interact with each other,e.g.,one-way quantum computation or delegated quantum computation,[11–15]in which a client remotely instructs a server to perform his private computation. Clearly,this model does not capture a special situation where the computation and the verification are performed by the same party. For instance,imagine that a material company purchases a quantum computer from a quantum computing company, they want to use it to simulate some complicated quantum systems. How can they convince themselves that the result of simulation is correct? Surely, an IP system may still work in this case if we allow workers to interact with the quantum computer back and forth. Nevertheless, they may prefer a way of more direct verification, i.e., they wish they could check the validity of computations according to a part of the output. Second,recall that in delegated quantum computations,most references related to this topic model an untrusted server as an honestbut-curious or malicious server. From the viewpoint of the protocol security,this is a reasonable hypothesis since the data privacy is an important factor in nowadays cloud computing.But, from a business perspective, to maintain a good reputation a sensible server should offer clients a correct computation experience as clients expect. For instance, imagine that two quantum computing companies both promote their quantum cloud services to you, will you choose the one who has a bad reputation due to offering terrible services? So, in this respect, a quantum server should perform a self-testing procedure to make itself sure that the computation task delegated by clients has been accomplished correctly. Even if a malicious server who wants to steal clients’information may plug some backdoor programs in clients’computation,in this case we hope a self-testing system can make the server give up this intention. Finally, self-testing is actually not a new idea in quantum information processing.In 2004,Mayers and Yao introduced the concept of self-testing in quantum apparatus.[16]They showed that a self-testing method can be used to check the unknown quantum apparatus. Then a lot of related works arose(see Ref.[17]for a lately comprehensive review). However, the idea of self-testing in those works is mainly related to device-independence in which the quantum apparatuses are treated as the untrusted devices and the self-testing is mainly used to check if those devices work as we desire. Besides that,we first note that most existing works only consider some special quantum processes,e.g.,generating a certain quantum state,performing a certain quantum measurement, and so on.To generalize those to a general case,we should consider this question from an abstract perspective,which means we should turn back to complexity theory and ask if there is a self-testing system such that given any quantum process it can verify the correctness of executions by itself. Although in Ref.[18]the authors had already put forward the concept of self-testing in quantum circuits.However,they did not promote this idea into the level of complexity classes. Note that Mckague et al. also introduced the concept of self-testing into interactive proofs for BQP problems[19](see Subsection 2.2 for further explanation on BQP problems),but in their work they still considered an interactive proof system with non-communicating quantum provers and a classical verifier.

Many different verification schemes for quantum computations have been proposed(a lately comprehensive review can be found in Ref. [9]), almost all of them use the language of interactive proof systems to describe the verification. Nevertheless,the basic idea behind these works is somewhat similar.Essentially,to verify whether a computation task f is honestly performed, the method used in the previous work is that the verifier hides some easy question g in the original task f,then the prover is required to compute this mixed task. When appropriate, the verifier retrieves information on the question g and checks if it is the same with his expectation. If so, the computation task f is thought to be performed correctly with a high probability, otherwise the verifier rejects. For example, in Ref. [20], to make sure that the quantum computation is performed correctly,each input qubit is attached by an extra quantum state then they are encrypted by a random Clifford operator,when a basic gate is required to apply on this qubit,the verifier first decrypts the whole state then checks that if the extra state is intact.If all qubits are authenticated,then the verifier accepts the outcome. Similarly,in Ref.[21],to guarantee that the sever performs the computation honestly, the client randomly sets some known qubits called traps in the universal graph state. Once any trap is triggered, the client checks its outcome. If the outcome does not accord with his expectation,the client rejects. From the previous works, we can see that one requirement must be met in this method: the simple question g must be blind for the prover, so that he can not bypass the question g to cheat the verifier. In this paper,we follow the same basic idea. Our main construction technique is to introduce the permutation in the computation. However, since we are considering a self-testing system, we do not need to hide the questions f and g. But, we do hope that the questions f and g are mixed up mutually in a way so that any deviation on f can be projected onto the output of g with a high probability. To do this, we use some extra ancilla qubits as a flag system, then randomly interpolate them into an extended circuit where the ancilla qubits are used to compute the function g while the rest qubits are used to compute the function f. This extended circuit is generated by a sequence of permutations operators and the additional function g is also generated by as a sequence of permutations operators,meanwhile this function g can be efficiently simulated by a classical computer. As a result,we will see that any problem in BQP class can naturally be equipped with a self-testing system if we allow some extra ancilla qubits to be added into the input.

The rest of this paper is organized as follows. We start by introducing some necessary preliminaries in Section 2. In Section 3,we define the self-testing system and state our main conclusions. Then in Section 4, we describe the construction of the self-testing system. Its completeness and soundness are shown in Section 5. In the final section, we discuss the link between the self-testing system and the interactive proof system.

2. Preliminaries

We assume that readers are familiar with the fundamental of quantum computation theory.[22]The n-qubit Pauli group Pnand the n-qubit Clifford group Cnare defined as follows:

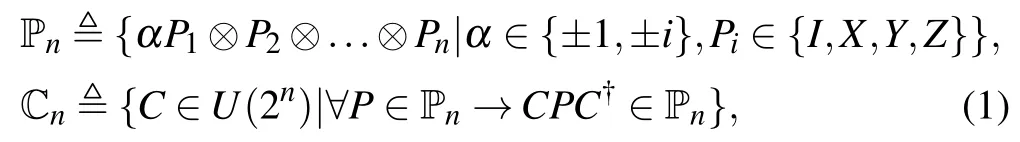
where U(2n) denotes the set of all n-qubit unitary operators.A well-known fact is that the n-qubit Clifford group can be treated as a subset of U(2n) generated by the Hadamard gate H,the phase gate S,and the controlled-NOT gate CX.Besides that,according to the Gottesman–Knill theorem[23]any polynomial size quantum circuit which is composed of H,S, and CX can be efficiently simulated by a classical computer.

In this paper, we consider the n-qubit quantum circuit in the form of U =UTUT−1...U2U1where each Uiis an n-qubit unitary operator consisting of a tensor product of at most n basic unitary gates from some universal gate set,and each basic gate in Uiacts on different qubits. We call such an operator Uia basic tensor gate. To further explain the meaning of tensor gates,we give a concrete example in Fig.1.

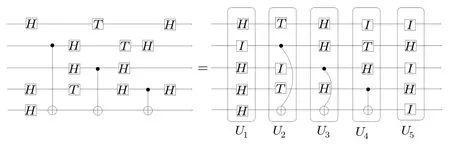
Fig.1. Given a quantum circuit U (the left) generated from the gate set{H,T,CX}, one can always normalize this circuit into a sequence of basic tensor gates. Some identity gates I may be needed in the normalized circuit.We can see that U=U5U4U3U2U1 where U1=H ⊗I ⊗H ⊗H ⊗H ⊗H,and so on.

2.1. Value and position permutations

Informally,a permutation can be viewed as a one-to-one function that its domain and range are identical.Following this way,we can define a value permutation on{0,1}nas follows.

2.2. The BQP class

The abbreviation BQP denotes the bounded-error quantum polynomial time, whose classical counterpart is the bounded-error probabilistic polynomial time, abbreviated as BPP. Simply speaking, the BQP class contains all problems that can be solved by a quantum computer in polynomial time.Similarly, the BPP class is the problem set that can be efficiently solved by a classical computer.Since we are only interested in problems in BQP class,in the last part of this section we formally introduce the definition of the BQP class.[9]

Definition 3A language or decision problem L ∈{0,1}*belongs to BQP if there exists a polynomial p(·)and a uniform quantum circuit family Q={Qn,n ∈N}, where each circuit has at most p(n)basic gates,such that for any x ∈{0,1}nthe following properties hold true:

• if x ∈L,then Qn(x)accepts with probability at least c,

• if x /∈L,then Qn(x)accepts with probability at most s,where c and s are known as the completeness and soundness parameters, respectively. Traditionally, we can set c = 2/3 and s=1/3. However, in full of generality, the rigorous requirement is that c−s ≥1/p(n)and p(n)is some polynomial function.[9]

3. Main results

In this work,our main conclusion is that for any problem in BQP class there exists an efficient quantum self-testing system,which can test if the computation result is reliable.Follow the same technicality used in Refs.[20,24],in the reminder of this paper we will consider promise problems,[25]instead of decision problems. A promise problem Π=(ΠYES,ΠNO)is a pair of disjoint sets of strings where the strings in the sets ΠYESand ΠNOare called YES and NO instances of the problem,and have answers YES and NO,respectively. Using promise problems can simplify our analysis, we only need to concern one special promise problem named Q-CIRCUIT problem.[20]

Definition 4The promise problem Q-CIRCUIT = {QCIRCUITYES,Q-CIRCUITNO}consists of two disjoint quantum circuit sets such that

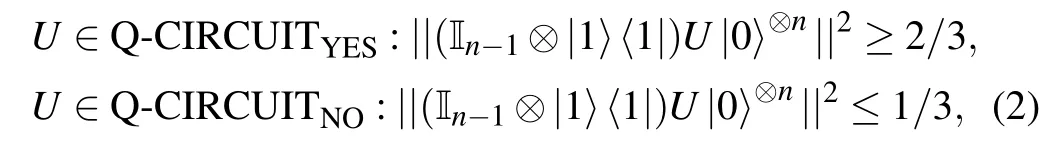
where U=UT,...,U1is a quantum circuit made of a sequence of gates acting on n input qubits.

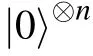
According to the definition of the BQP class, given any problem in BQP class there exists a uniform quantum circuits family Q={Qn:n ∈N} such that each circuit Qncan take n qubits as an input then output a result of the problem. Intuitively,in order to verify the output by the circuit Qnitself,one can introduce some ancilla qubits in the circuit Qnand use the output state of those ancilla qubits to indicate if the computation has been performed correctly.

Definition 5A promise problem Π=(ΠYES,ΠNO) in BQP class is said to have a self-testing system if and only if there exists a polynomial-time generated family of uniform quantum circuits Q = {Qn: n ∈N}, where each circuit Qntakes n+d input qubits and produces one output qubit,the first n qubits ρinis the input of the problem while the additional d qubits ρselfis used for self-testing. The following properties hold true:

• (completeness)if ρin∈ΠYES,then Pr[Q accepts(ρin,ρself)]≥c;

• (soundness)if ρin∈ΠNO,then Pr[Q accepts(ρin,ρself)]≤s,

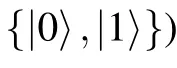
The class of promise problems having a self-testing system is denoted by BQPST. In brief,in this work we show the following theorem.

Theorem 1BQP=BQPST.

The main proof of the above theorem is shown in Section 5. In the next section,we first describe the construction of our self-testing system.

4. Self-testing systems for BQP problems

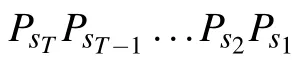
4.1. Generating algorithms

?

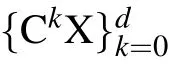
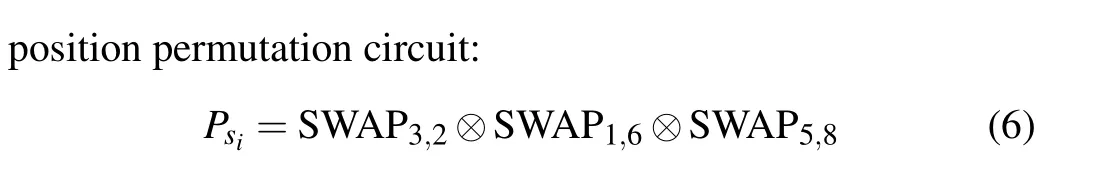
and the corresponding subscript order sican be obtained from the following procedures:

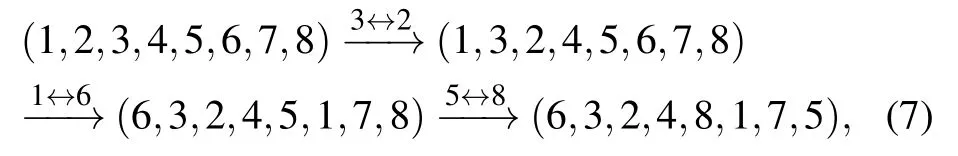
4.3. Self-testing system

The main algorithm of a self-testing system for a quantum computation can be divided into three stages.The specific procedure is described as follows.

?

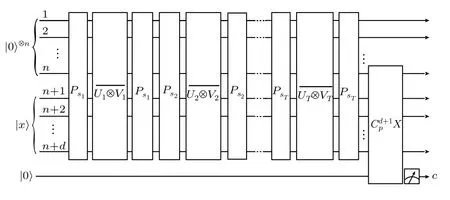
Fig.2. The basic circuit framework of a self-testing system for a quantum circuit U.

5. Completeness and soundness

5.1. Completeness

Now suppose U ⊗V is a YES-instance of the promise problem Q-CIRCUIT, where the circuit V can be viewed as a redundant input for U, then we can infer that if the protocol is performed correctly,then the self-testing system accepts with probability at least 2/3.

5.2. Soundness

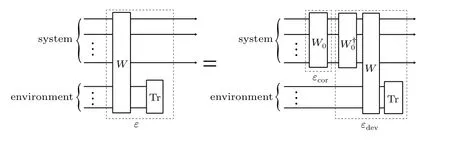
Fig.3. Any quantum operation ℰ on a system can be modeled as a unitary operation W on the system and an extra environment,[22] let W0 be the correct quantum computation circuit then we can obtain W =.

Then, let ℰ be the whole quantum operation during the protocol (including any possible deviation), it is easy to see that any such an operation ℰ can be decomposed as a correct computation ℰcorfollowed by another deviation ℰdev(see Fig.3),that is,

Finally,we define the projection operator as follows:

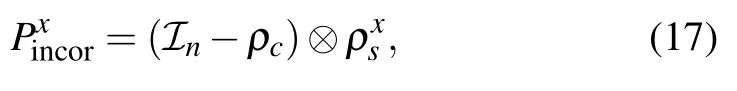
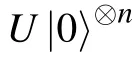
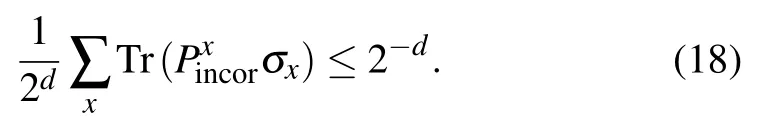
Our basic argument is based mainly on the proof techniques in Refs. [20,24]. The complete proof is shown in Appendix B. Now according to the conclusion in Eq. (18),we immediately obtain that if U ⊗V is a NO-instance of QCIRCUIT,then no matter what deviation ℰdevhappens during the protocol,the soundness parameter s always satisfies that

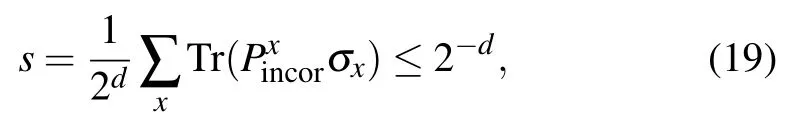
where we can see that c −s ≥2/3 −2−d≥1/poly(n), so it completes the proof of the main theorem.

6. Links between self-testing systems and interactive proof systems

We showed that BQP=BQPSTin Section 5. Since we have already known that BQP = QPIP[20,24](the abbreviation QPIP denotes the quantum-prover interactive proofs), as mentioned most previous works considered verifiable quantum computation using the language of the QPIP class, it follows immediately that BQPST=QPIP, which means for any BQP problem there exists at least a pair of verification schemes: a self-testing system and an interactive proof system. A natural question is whether we can construct a system from another one. Clearly, an interactive proof system can be treated as a special kind of self-testing systems if we treat the prover and the verifier as one single party.So,in this paper we are only interested in one direction:constructing an interactive proof system from a self-testing system. In the following content, we will show that given a self-testing system one can easily construct an equivalent interactive proof system. The equivalence means that if a self-testing system is c-completeness and ssoundness,then the same completeness and soundness parameters hold in the constructed interactive proof system. Clearly,to construct an interactive proof system from the self-testing system,a simple way is to hide the complete self-testing system from the prover,which can be easily done by blind quantum computation(BQC).

6.1. Constructions via blind quantum computation

We list two implement methods in the following contents,the first one is based on universal blind quantum computation protocol,[12]and the second one is based on secure assisted quantum computation protocol.[27]

Clearly,the above construction is efficient,this is because all subroutines called by the verifier and the prover can be done in polynomial time. Moreover,the new interactive proof system has the same completeness and soundness parameters,this is because if both verifier and prover are honest, the UBQC protocol will always output the correct outcome. Besides that,in Ref.[12],the UBQC protocol can be implemented in a way such that any interfering prover either fails to alter the computation or escapes from been detected with an exponentially small probability.

It is worth noting that the above construction requires the verifier to have some quantum capacity. Typically,in the universal quantum computation protocol, the verifier is required to have an ability to prepare some random single qubits,[12]while in the secure assisted quantum computation protocol,the verifier is required to have an ability not only to prepare some random single qubits but also to apply some quantum operations[27](in Ref.[24],the requirement is reduced to prepare some random single qubits).

7. Conclusions

At final, we briefly discuss our work. First, we showed that any BQP problem admits a self-testing system which can be used to verify if the computation circuit is performed correctly. The main technique using in our protocol is introducing permutations in the computation circuit. By the positionpermutation operation, the positions of all qubits in the circuit including ancilla qubits are rearranged randomly. By the state-permutation operation, an additional quantum computation which can be efficiently simulated by a classical computer is introduced, the computation result of this additional circuit is used as a witness that checks if the original computation circuit is performed correctly. Second,we showed that given a self-testing system one can easily transform it into an equivalent interactive proof system. There are two different but equivalent implement methods, and they both require the BPP verifier to have some quantum capacity, that is, the verifier can prepare some single qubits. Finally, it is worthy to mention that although our protocol is designed for detecting any possible deviations during the execution by a self-testing way,it does not include the innocent noise during the computation, for example the quantum gate errors. Nevertheless, it is totally possible that we can use some quantum error correction codes to overcome this shortcoming. Consequently, we will consider a fault-tolerant self-testing system in our further works.

It is natural that most of verifiable quantum computation protocols require the verifier to have some quantum capacity except for considering the post-quantum security[28,29]or the multiple entangled and non-communicating provers.[30,31]Indeed, many researchers believe that there is no interactive proof system such that the prover is restricted to a fully BQP machine while the verifier is restricted to a BPP machine(for example,see Ref.[32]). At first glance,this is an evident conclusion because when a verifier delegates a computation to a prover,if all information sent to the prover is classical,then the BQP prover can generate plenty of duplicates and run those computations locally. As a result,the prover can definitely obtain the computation result,then from the perspective of blind quantum computation,we cannot accomplish the verification.

Appendix A:The value permutation circuits

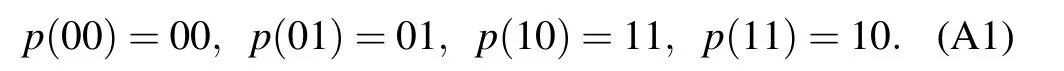
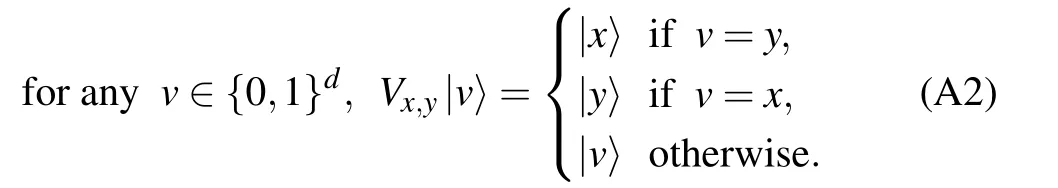
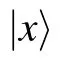
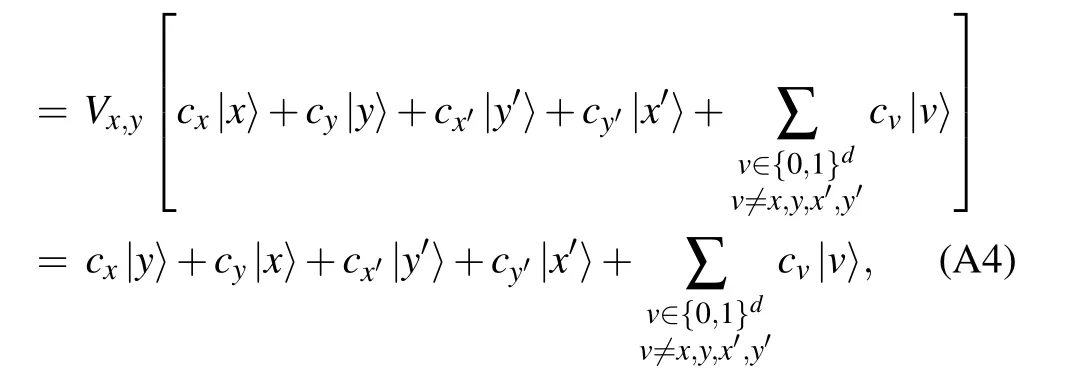
similarly,

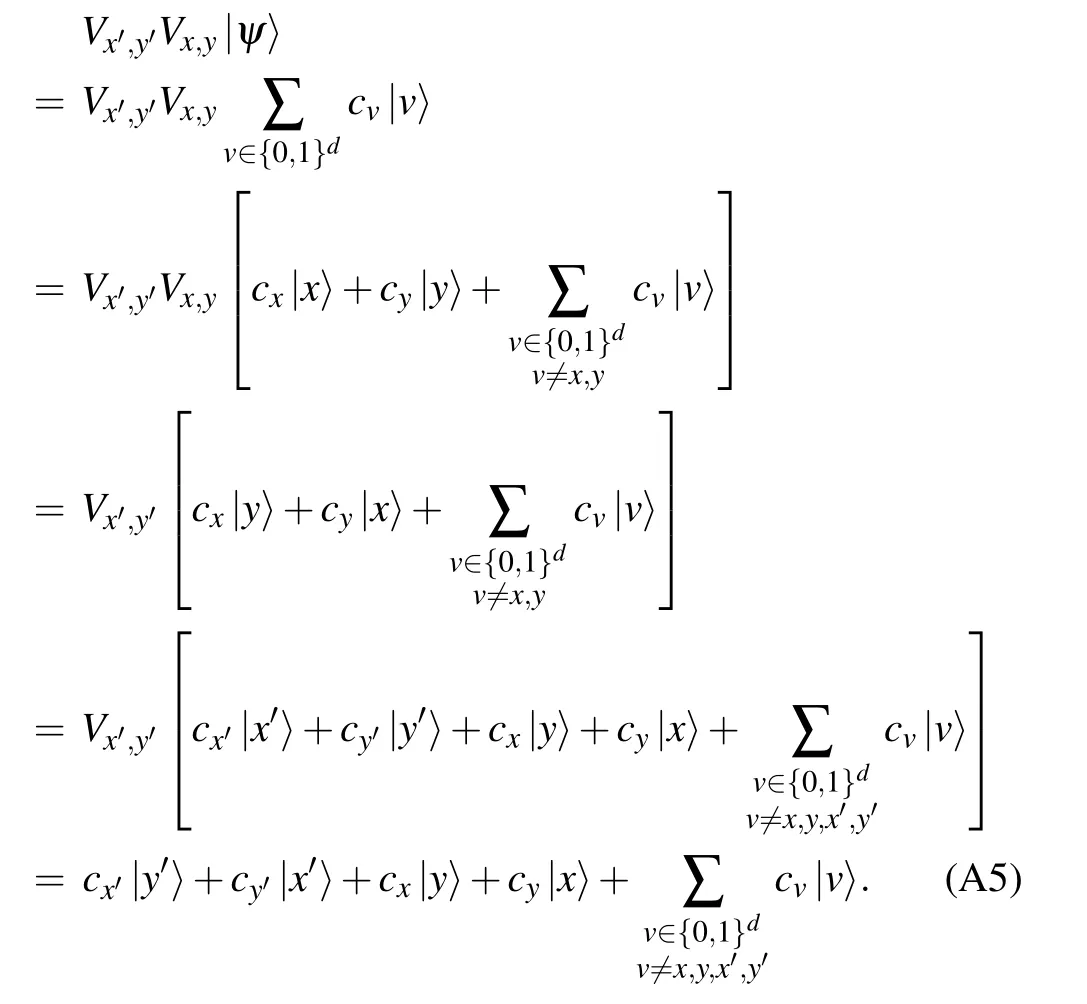
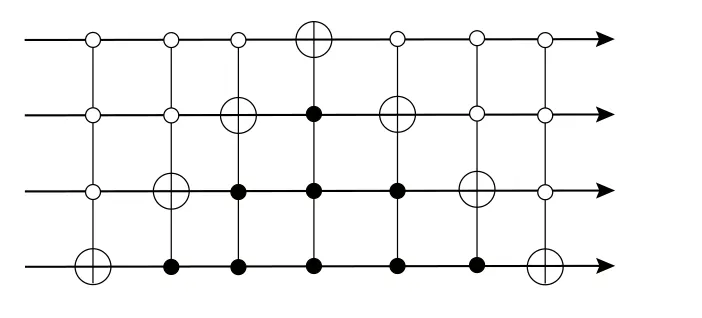
Fig.A1. The quantum circuit V0000,1111 consists of a sequence of 3-qubit controlled-NOT gates. Here we use the open circle notation to indicate conditioning on the qubit being set to zero,while a closed circle indicates conditioning on the qubit being set to one,see Ref.[22]for further explanations.

From the above two equations, one can immediately obtain that for any distinct x,y,x′,y′, the unitary operators Vx,yand Vx′,y′satisfy the following relation:

Now using the above conclusion, one can easily check that for any x ∈{0,1}d,the following equation holds true:

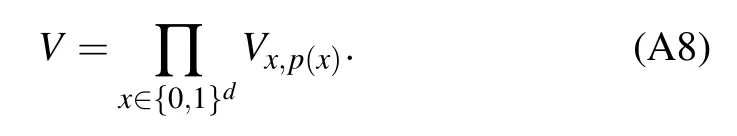
Appendix B:The proof of inequality(18)

First, according to the quantum information theory,[22]we know that any quantum operation admits an operator-sum representation, thus the deviation ℰdevin Eq. (16) can be expressed as follows:

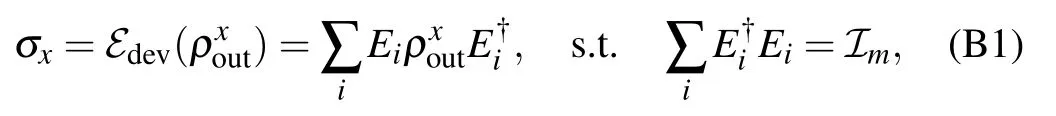
where the operator ℐmdenotes the identity operator in Pauli group Pm. Moreover, since the Pauli group can be treated as a basis to the matrices, so each operator Eican be uniquely expressed as a combination of n-qubit Pauli operators,that is,

where all coefficients {αi,P} are possibly complex numbers and it is easy to check that the numbers satisfy the following equation: