地下泵站厂房围岩弹塑性三维有限元分析
2021-05-06何帅
何 帅
(新疆水利电力建设总公司,乌鲁木齐 830000)
0 引言
地下泵站厂房围岩的稳定性是地下厂房设计及施工的重点问题。因此,采用有限元方法对复杂条件下的地下厂房开挖施工过程仿真计算是很有必要的。国内许多学者对地下厂房的稳定性做了很多建设性的研究:曾志勇[1]依托溧阳抽水蓄能电站地下厂房,采用三维有限元数值计算的方法,对地下硐室开挖工序及围岩变形进行了分析,最终确定了施工方案。孙军[2]以乌干达卡鲁玛水电站为依托,对其地下厂房围岩的应力及位移做了计算研究,通过对比,得出了最优的施工方案。任少龙等[3]依托拉哇水电站地下厂房,采用有限元法,对地下厂房进行三维非线性数值模拟计算,对围岩的应力、位移和塑性区的规律进行研究,为开挖及支护提供计算支撑。
诸多学者[4~8]在地下厂房稳定性方面的研究为地下厂房稳定性的分析角度、计算方法方面提供了指导。本文运用有限元数值计算的方法,对新疆某工程地下泵站厂房在分层开挖条件下主厂房的围岩应力、位移及塑性分布进行计算,旨在为主厂房的施工措施、支护措施提出建议。
1 地质概况
新疆某泵站拟采用地下厂房方案,推荐方案厂房埋深260 m。厂区岩石主要为华力西晚期变质花岗岩、斜长花岗斑岩夹闪长岩,颜色为灰白~灰黑色,块状构造,岩石受区域动力作用轻度变质,矿物间发生挤压变形,具有定向排列,局部形成弱片麻理构造,片麻理产状30°~50°SE∠46°~64°,与构造主应力基本一致,分析认为受构造应力作用下使原来的斜长花岗斑岩、花岗岩产生变质。根据钻孔资料反应,上部岩石片麻理构造不显著,随着深度增加岩石片麻理化增强,也说明了最大水平主应力随深度增大而变大。岩石片麻理多挤压紧密,片麻理间距2~3 cm,岩石节理裂隙不发育,仅局部发育少量节理,间距大于100 cm,裂隙面粗糙、起伏,无充填。经矿物成份分析,岩石中石英含量占25%~30%,最高约35%。
根据地表地质测绘并结合物探、钻探、试验资料综合分析,依据《水利水电工程地质勘察规范》(GB50487-2008)围岩详细分类,主要以控制围岩稳定的岩石强度、岩体完整程度、结构面状态、地下水和主要结构面产状五大因素之和的总评分为基本判据,围岩强度应力比为限定判据。并结合钻孔岩石质量指标RQD、岩体结构、岩体透水率、岩体波速、岩体节理系数、裂隙平均间距、岩体弹变形模量、岩体坚固系数、岩体弹抗系数及围岩岩爆等,综合划分地下厂房围岩类别为Ⅲ类围岩。
2 数值计算模型
2.1 本构模型
本构模型是岩土材料力学性质的经验性描述,表达的是外载条件下岩、土体的应力-应变关系,因此本构模型的选择是数值模拟的一个关键性步骤。对具体的工程分析选择本构模型时,必须考虑到工程材料的已知力学特性和本构模型的适用范围。只有当选择的本构模型与工程材料力学特性契合度较高时,其选择才是合理的。
岩土工程中,根据岩石力学特性,数值计算时常采用弹塑性本构模型。结合本工程地质条件,选用理想弹塑性本构关系,摩尔库伦条件作为围岩屈服的准则。摩尔库伦屈服准则为剪切破坏准则,其剪切屈服面函数为[9,10]:
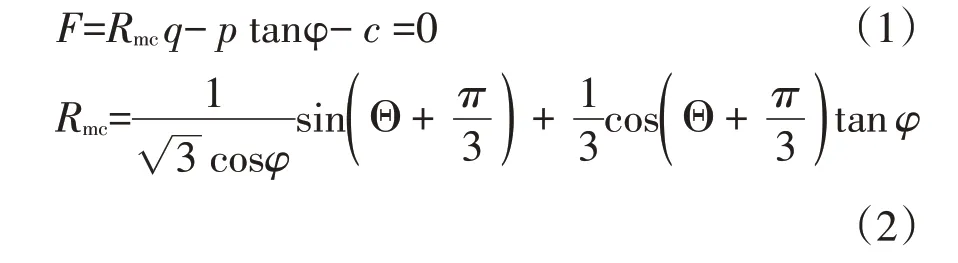
式中:φ为q-p应力面上的摩尔库伦屈服面倾斜角;c为材料的粘聚力;Θ 为极偏角,定义cos(3Θ)=(J3)3/q3,J3为第三偏应力不变量。
由于摩尔库伦准则屈服平面存在尖角,为避免尖角影响使得尖角处出现塑性流动方向不唯一现象,采用椭圆函数作为塑性面,其函数表达式如下:

式中:Ψ为材料剪胀角;C0为未发生塑性变形的初始凝聚力;ε 为子午面偏心率;Rmw为控制塑性势面的参数,按式(4)计算。
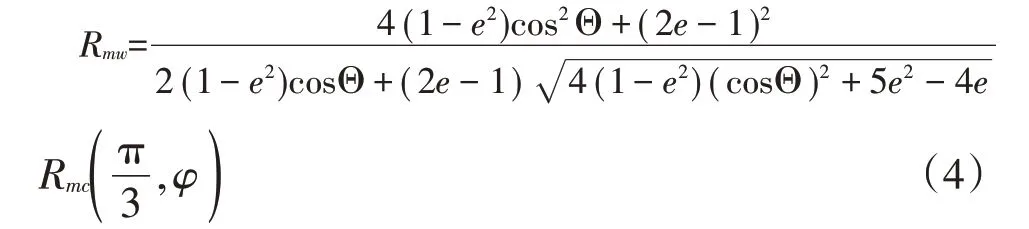
式中:e为π面上的偏心率,按式(5)计算。

2.2 几何模型及网格划分
泵站主厂房几何模型尺寸如图1所示。主厂房几何尺寸为22 m×50 m×51.35 m,整体模型几何尺寸为275 m×132 m×310 m,模型尺寸大小满足边界影响要求。
根据工程实际情况,建立三维有限元模型并划分网格(见图2)。如图2 所示,模型完全采用六面体网格,采用20 节点二次实体单元。模型共划分160 080个单元。

图1 主厂房几何模型

图2 有限元计算模型及网格划分
2.3 计算参数及边界条件
根据实验室岩石标准力学试验得出岩石的物理力学参数,据此选取厂房围岩的物理力学参数(见表1)。

表1 厂房围岩物理力学参数
整体模型边界条件采用上部压力边界,即根据整体模型尺寸及埋深设定压力,模型底面为全约束条件,整体模型侧向面采用法向约束。主厂房采取分层分步开挖方案,主厂房开挖完成共计10 步,各开挖步开挖层高如下:第1步(拱顶)7.9 m;第2步2 m;第3~8 步各5 m;第9 步6.35 m;第10 步5 m。开挖示意图见图3。
3 计算结果分析
3.1 围岩应力场
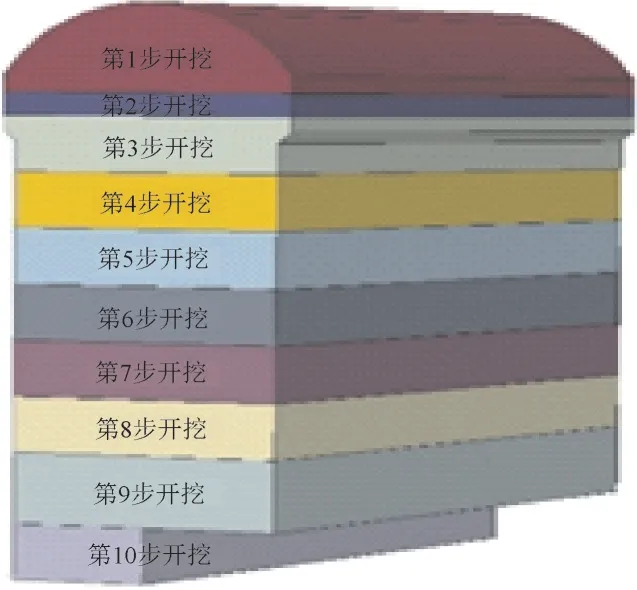
图3 主厂房分布开挖示意图
根据前述有限元计算模型及参数,采用有限元计算软件进行三维有限元计算,得出地下厂房主厂房围岩在各个开挖步骤下的最大主应力场、最小主应力场分布情况。受篇幅限制,图4、图5给出了第1、4、7、10 步围岩的最大主应力及最小主应力分布云图,其中拉为正,压为负(下同)。
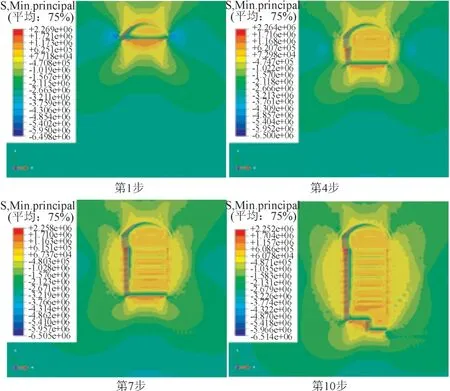
图4 各开挖步骤下厂房围岩最大主应力分布云图(Pa)
由图4可以看出,第1步开挖顶拱部位时,围岩最大主应力最大为2.269 MPa,为拉应力,位于底边局部应力集中区,顶拱部位小部分区域受到0.85 MPa 拉应力,厂房左右侧边墙中部呈纺锤形区域受到拉应力,最大值为0.75 MPa。开挖第4步时,厂房岩锚梁部位围岩最大主应力为2.264 MPa,呈拉应力,同时,顶拱、底边及侧边墙均有拉应力区域,局部拉应力集中区域约为1.16 MPa。开挖至第7 步时,围岩拉应力区域逐步增大,在边墙部位,围岩拉应力呈现“条带”特征分布,岩锚梁部位围岩最大主应力略有调整,为2.258 MPa,厂房顶拱、底边及侧边墙拉应力区域扩展,围岩最大主应力场受分层开挖方式影响显著。开挖完成(第10步)时,厂房围岩最大主应力为2.252 MPa,围岩应力场进一步发展,顶拱受拉区变化不显著,相比而言,底边及侧边墙均有拉应力区域发展,厂房底部受到隆起作用拉应力较为显著,局部拉应力约为2 MPa,据此可以推测,厂房底部可出现隆胀破裂现象。

图5 各开挖步骤下厂房围岩最小主应力分布云图
由图5可以看出,在厂房完成第1步开挖时,围岩最小主应力为22.68 MPa,最小主应力集中于上下游边墙底角及深度为1.8 m 围岩局部区域,围岩受开挖作用,应力重分布使得在厂房上下游底部受到压应力集中,由于围岩在载荷作用下进入塑性阶段,发生塑性破坏,重应力耗散释放,边墙部位应力降低,表现为应力集中区内移。围岩开挖至第4 步时,最小主应力最值在应力重分布作用下降低,为18.57 MPa,位于边墙内一定深度处。开挖至第7步时,围岩最小主应力最值没有变化,但在上下游边墙与左右侧边墙夹角处出现压应力集中,达18.59 MPa,上下游边墙处压应力区域进一步扩大,压应力数值降低,约为14 MPa。开挖完成后,随塑性破坏的发展,上下游边墙的最大压应力区域进一步内移,各边墙夹角处出现压应力集中,在岩锚梁与左右侧边墙处尤为凸显,可达18.69 MPa。
3.2 围岩位移场
图6 为围岩的位移场分布云图,从图6 可以看出,随开挖步骤推进,厂房围岩变形量逐步增大。由云图可以看出,在第1~4步开挖中,厂房变形量主要位于顶拱及底边。继续向下开挖,最大变形部位由顶拱及底边变为上下游边墙,变形量也有所增大,由顶拱处最大1.83 cm 变为上下游边墙最大3.28 cm。因此,厂房开挖时,应考虑适当的预留变形量,以免造成欠挖。
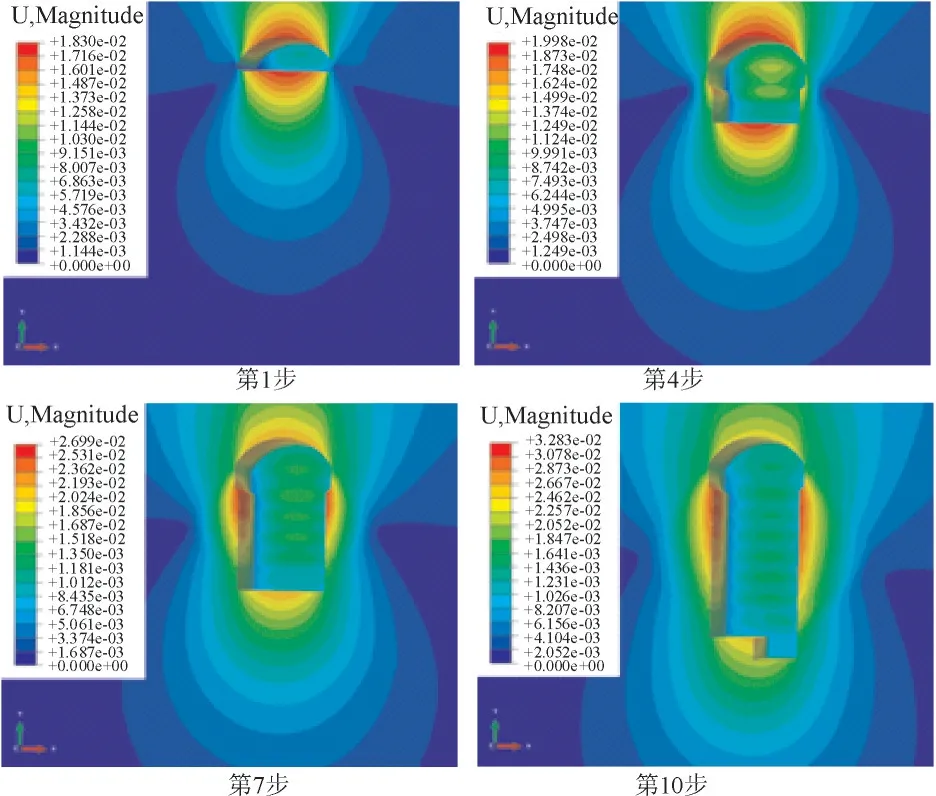
图6 各开挖步下厂房围岩塑性区分布云图
3.3 塑性区特性
图7 为各开挖步骤下厂房围岩塑性区分布云图。从图7可以看出,围岩塑性区随开挖进程的推进,塑性区范围逐步扩大。等效塑性应变最大值位于顶拱与边墙交接处,由此可预测,在此开挖方式下,该部位围岩较其余部位破坏程度大,可能会出现破碎掉块现象。另外,由计算结果可以看出,塑性破坏主要位于边墙围岩上部区域,开挖步骤对塑性区分布的影响较为明显。边墙塑性区也出现“条带状”特征,与围岩应力场分布特性一致。计算结果表明岩锚梁处围岩塑性区深度约为6m,由此,建议锚杆长度应大于该深度,以伸入弹性区,保证其应有的支护效果。
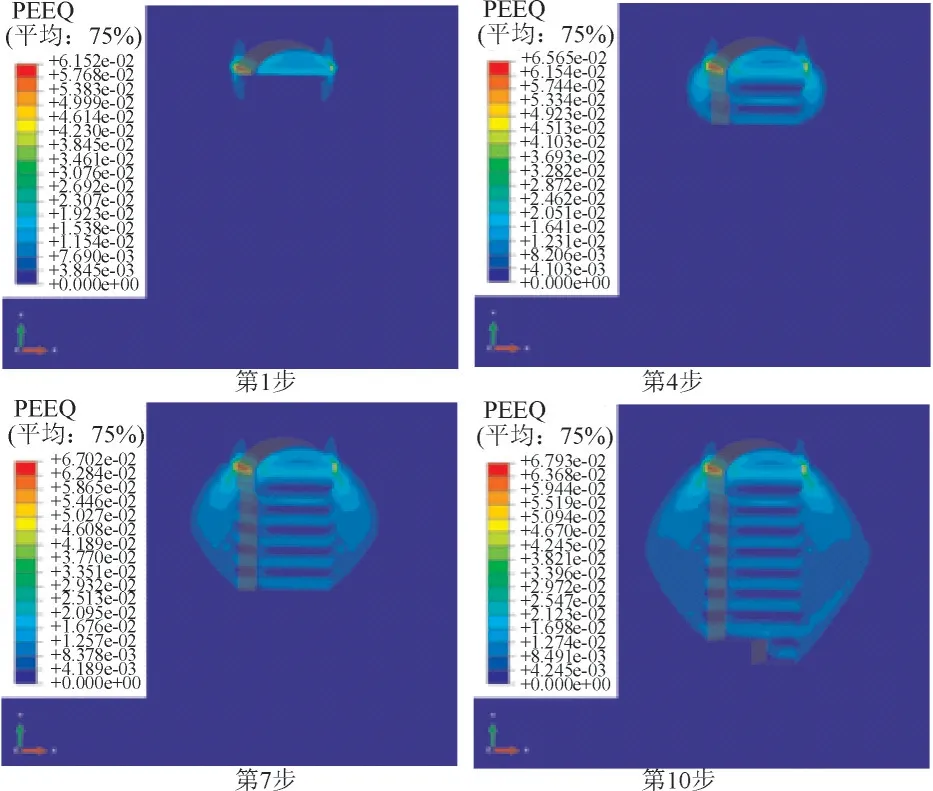
图7 各开挖步骤下厂房围岩塑性区分布云图
4 结语
本文依托新疆某大型泵站工程,基于弹塑性理论,采用有三维限元数值计算的方法,对地下泵站厂房主厂房分层开挖条件下围岩的应力场、位移场、塑性区特性进行了计算分析,结果表明:
(1)厂房围岩受开挖步骤影响显著,边墙处应力呈现“条带”状分布特性。
(2)围岩位移最大值所在位置随开挖推进呈现出“先顶拱底边、后上下游边墙”的变化特性。
(3)根据塑性区深度,设计喷锚支护方案,锚杆应伸入围岩弹性范围内。岩锚梁处围岩锚杆应大于6m且满足锚固长度。
(4)上下游边墙上部围岩受力特性较差,塑性破坏较为严重,建议优化施工方案。
