基于GAMS模型的配水系统阀门与泵的优化调度研究

郑 丽

（贵州新中水工程有限公司，贵阳 550000）

0 引言

过去10～20年里，由于泄漏问题，管网输水过程中损失了大量的水，同时在水处理和抽水方面耗能过高[1]。许多学者对复杂大型给水管网络（WDN）进行了运营改进，通过引入压力控制算法可以减少泄漏，从而节省清洁水[2]；通过优化泵的运行，可以减少用于泵送的能量[3]。通常会配备变速驱动装置，可以通过操纵泵速来控制泵出口压力。如果减压阀（PRV）上游有泵而没有任何中间水箱，则可以通过调整管网上游部分的泵来降低PRV 入口压力。因此对于某些WDN 来说，可以将泵运行优化与压力控制结合起来。

泵的优化方案可以基于时间序列，本文考虑的是时间排程法[4]。现有文献中大多数WDN 优化方法是通过水力模拟器或简化的质量平衡模型作为其优化过程的关键元素，并且通常将小规模的供水系统作为案例研究。本文提出使用液压建模作为输入，不需要电子地图模拟器来产生可行的解决方案。

1 方法概述

本文研究的对象包括存在压力泄漏网络的水力模型、简化的PRV模型。成本函数代表水处理和泵送的总成本，采用过载泵的管网模型成本情况见图1。由图1 可知，过载的泵在两个方面导致了总成本过高。首先，它导致高能耗。其次，它导致高压，从而增加泄漏，这意味着需要从源头抽取更多的水。因此，优化模型通过最小化总成本来减少能源消耗和管网泄漏。

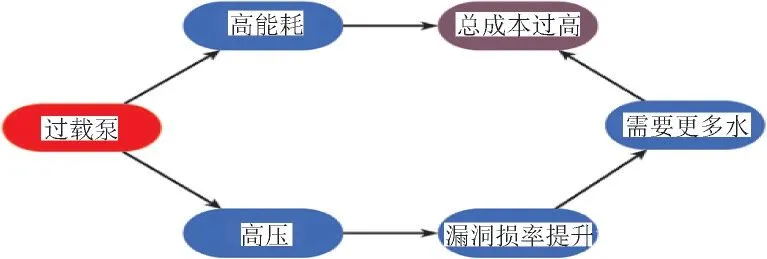
图1 采用过载泵的管网模型成本情况

为了减小优化问题的规模，使用模块缩减算法简化了全液压模型。在简化模型中，所有储罐和所有控制元件（如泵和阀门）保持不变，但管道和节点的数量显著减少。所考虑优化问题的一些决策变量是连续的（如产水量、泵速、阀门开度），一些是整数的（如打开泵的数量）。包含连续变量和整数变量的问题被称为混合整数问题，在解决该问题的过程中，重点是获得连续的时间序列，可通过时间序列离散化算法求解。

2 供水网络调度持续优化

首先，使用一个简化的管网水力模型和一些相关数据，目标函数由主软件模块以数学建模语言GAMS 自动生成[5]；随后，调用CONOPT 的非线性规划求解器来计算连续优化解；然后，最佳解决方案从CONOPT 反馈到主软件模块，对其进行分析和进一步处理。所有变量的原始数据直接从加载网络结构的EPANET输出文件中获得。

2.1 GAMS WDN优化模型

2.1.1 连接节点

对于连接节点，通过质量平衡方程计算：

式中：Λc是节点分支关联矩阵；q是支流向量；dc表示需求向量；lc表示按式（2）计算的泄漏向量。

式中：P 表示节点压力矢量；α 表示泄漏指数；k 表示泄漏系数矢量。

2.1.2 泵站

假设泵站中所有的泵都具有相同特性。除了强制泵站沿其扬程流量曲线运行的标准水力方程式外，还为每个泵站添加了以下约束：

式中：Δh表示进水口和出水口之间的扬程增量；u表示运行中的泵数。

当一些泵站串联时，没有中间水箱和带有止回阀的旁路，式（3）可防止泵站在开启时以负扬程运行。但是，式（3）允许泵站入口和出口节点之间存在水头负增加，当它关闭时，水可以通过旁路流动。因此对于泵站串联的网络，需要式（3）来确保解的物理可行性。

采用对泵站功率直接建模，引入IF-ELSE公式：

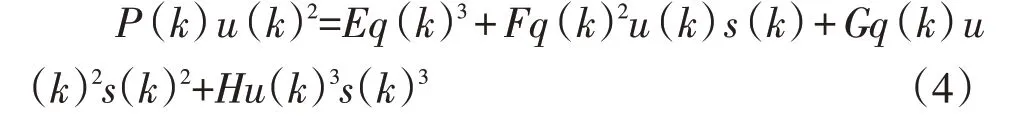
式中：E、F、G、H 是给定泵站的恒定功率系数；Q 是流量；P 是消耗功率；s 是归一化获得的额定转速。由于系数E 和F 比G 和H 小，为了使大规模模型更容易求解，假定E=0和F=0，即消耗功率与泵站流量成线性关系。

2.1.3 阀门

在本文提出的方法中，假设所有的可控阀都是PRV（控制变量是PRV 的出口压力）或FCV 调节阀（控制变量是阀门流量）。由于FCV 和PRV 都可以调节阀门的水头损失，并且它们的流向是已知的，为了减少模型的非线性，建议将FCV和PRV都表示为不等式：

两种阀门类型之间的差异是它们的控制变量。因此，阀门流量由质量平衡方程定义。止回阀由以下公式描述：

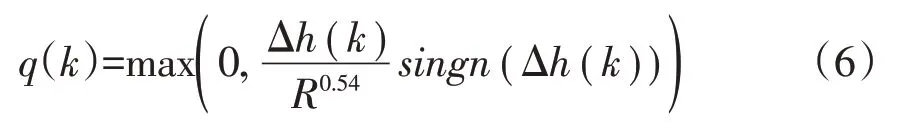
式中：R是恒定的阀门阻力，公式确保仅当阀门流量大于零时，阀门水头损失为正值；当流量为零时，水头损失可以取任何负值。公式（6）中的术语符号（Δh）可以定义为：

2.2 目标函数

目标函数是最小化水处理和抽水的总能源成本。抽水成本取决于用电量和抽水时间内的电费。对于给定的时间步长τc，在给定的时间范围内考虑的目标函数由下面的方程式描述：

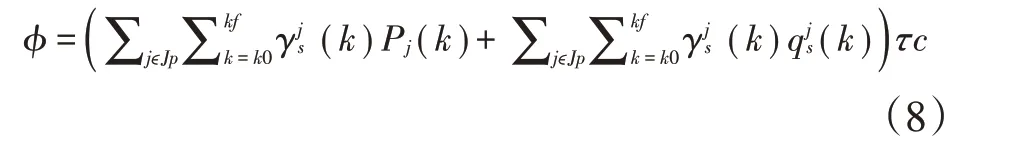
2.3 运行约束

除了前文定义的水力模型的约束外，为将系统状态保持在其可行范围内，应设立运行约束：

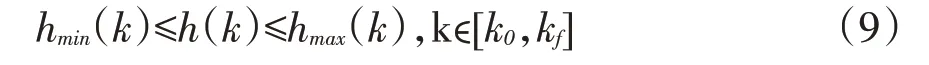
必须对关键连接节点处的水头施加上述约束，以便在整个供水管网中保持所需的压力。另一个重要的约束是水箱的最终水位，这样最终水位不会低于初始水位；如果没有设定上述限制，最低成本的优化将导致水箱水位为0。控制变量也同样受到这些约束。

2.4 连续时间序列的离散化

本文的重点在于连续优化，因此考虑了一种离散化算法，算法通过以下步骤进行：

（1）加载GAMS/CONOPT程序。

（2）对于连续泵控制循环的每个泵站，计算每个时间步长的累计舍入误差。累积的舍入误差在随后的时间步长中使用，通过用户定义的阈值来决定打开的泵的数量。

（3）生成新的GAMS 代码，其中每个泵站和每个时间步长打开的泵数量是固定的，即如步骤2 中计算的那样。管网中所有流量和压力的初始条件由GAMS/CONOPT在持续优化期间计算得出。在此GAMS 代码中，每个泵站和每个时间步长打开的泵数量不再是决策变量，而是强制参数。但求解器（CONOPT）仍然可以改变泵的速度，并且可以调整阀门流量以匹配开启的泵数量。

（4）调用GAMS/CONOPT，然后加载整数优化解的结果。

（5）在连续优化过程中，只有当该泵站的所有泵都关闭时，泵站流量才能为零。然而，在长时间范围内的整体优化过程中，泵站被迫在特定的时间步骤期间开启某一个泵，但是该泵不能在该时间步骤输送所需的压头，因此泵流量为零。如果发生这样的事件，则重复上述步骤3和4。

3 实例应用

3.1 网络概述

研究的供水管网由12363 个节点、12923 条管道、4 个水库、9 个水箱、6 个泵站的13 台水泵和315个阀门组成。该系统由1个主要来源（水处理厂）和2 个小规模进口供应。所考虑的WDN 包括复杂的结构和泵站之间的相互作用，例如没有中间水箱的串联泵站、有旁路的泵站、定速和变速泵站的混合、将一个泵站的流量分流到多个水箱的阀门、从增压泵供给的PRV或从PRV供给的增压泵。

由于其复杂性，没有完全描述完整的网络结构；图2 展示了网络中间的泵站配置。由于泵站旁路，当串联的两个泵站之间的需求量较低时，可以关闭其中一个泵站，水仍能以足够的压力到达管网的下游部分。

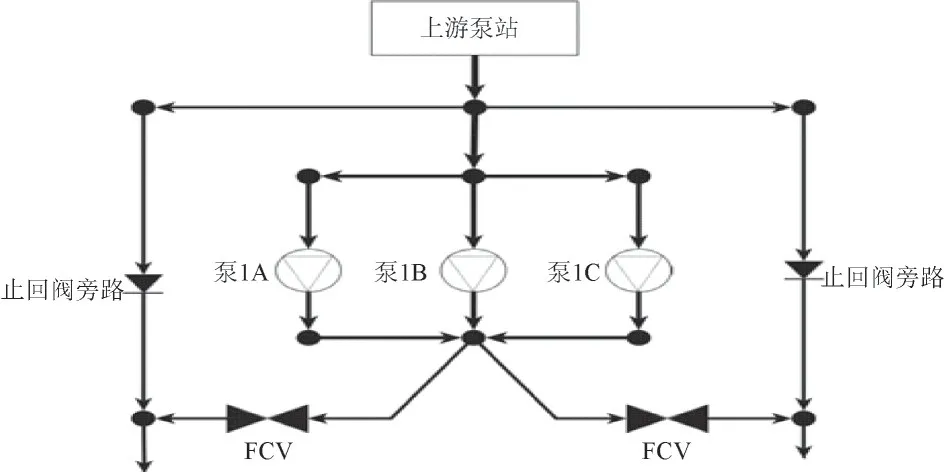
图2 带有止回阀旁路和流量控制阀的泵站结构

3.2 水工模型的制备与简化

在应用自动模型降阶算法之前，需要进行一些手动模型准备，包括以下步骤：①将模型从Darcy-Weisbach 公式转换为Hazen-Williams 公式；②两个水库通过永久封闭的管道连接到系统；③根据相似的压力轨迹将两个相连的水箱合并成一个直径适当的水箱；④拆除了约200个永久关闭的隔离阀；⑤若干具有固定开度的阀门已更换为具有同等阻力的管道；⑥具有控制规则TCV（温度控制阀门）被等效的FCV替换；⑦指定启闭控制规则的管道被替换为FCV。

通过上述修改能够进一步减少网络元件的数量，如果隔离阀没有被移除，则自动模型简化算法将把它们作为控制元件来对待，从而将它们保留在简化的模型中。随后，应用了自动模型降阶算法；降阶规模如表1所示。

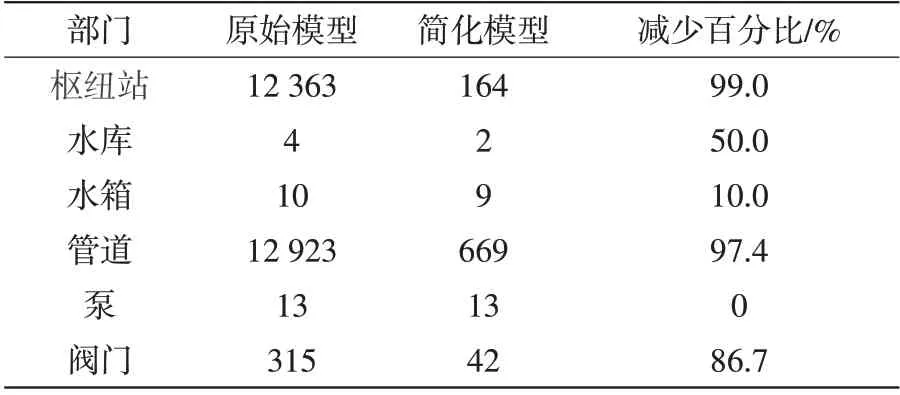
表1 原始模型和简化模型中的元素数量

为了验证简化模型是否能模拟原始模型，计算了泵/阀的流量轨迹和水库/水箱扬程轨迹的R2拟合优度，结果表明：简化后的模型较好地再现了原模型的水力特性。泵和阀流量的R2在最不利情况下为0.94，在大多数情况下为0.99。水库和储罐的R2在最不利情况下为0.5，其他的R2在0.98 到1.0 之间，最大的差异发生在离主要污染源最远的一个小水箱，可忽略不计。

3.3 调度结果示例

优化算法在几个情景下分别运行，这些情景对允许的水箱液位和允许打开的泵数量有不同的限制。在所有情景下，假设每个水箱的初始液位与所提供的EPANET 模型相同，不同元素中的压力和流量约束要么由自来水公司提供，要么假定在所有情况下都保持不变。在每种情况下，都会自动生成GAMS 代码，并且CONOPT 会找到最优的连续解决方案；随后，决定扩展模型的边界，增加一个泵站和一个水箱。在简化的EPANET 模型和描述泵站约束的附加文件中进行更改后，调度器成功地生成并求解了更新的优化模型，而不需要对算法进行任何更改。在普通计算机上，优化24 h 和优化7 d 时间分别需要大约5 min和1 h。

一个7 d方案的泵站运行随时间的变化情况和水箱液位轨迹分别见图3、图4。在最便宜的电价期间，由于抽水增加，水箱水位增加；而在电价高峰期，水箱水位下降。在所有情景下，还观察到水箱在本周中期缓慢排空，然后开始装满，因为最终液位必须至少是初始液位。这些观察结果表明：如果其他政策允许，为了降低运行成本，该水箱的运行水平应该低于其在EPANET模型中的初始水平。值得注意的是，不应对当前和优化后的操作进行比较，因为提供的数据仅考虑了一天的操作，而在特定的一天，大多数水箱的最终液位与初始液位相差甚远。

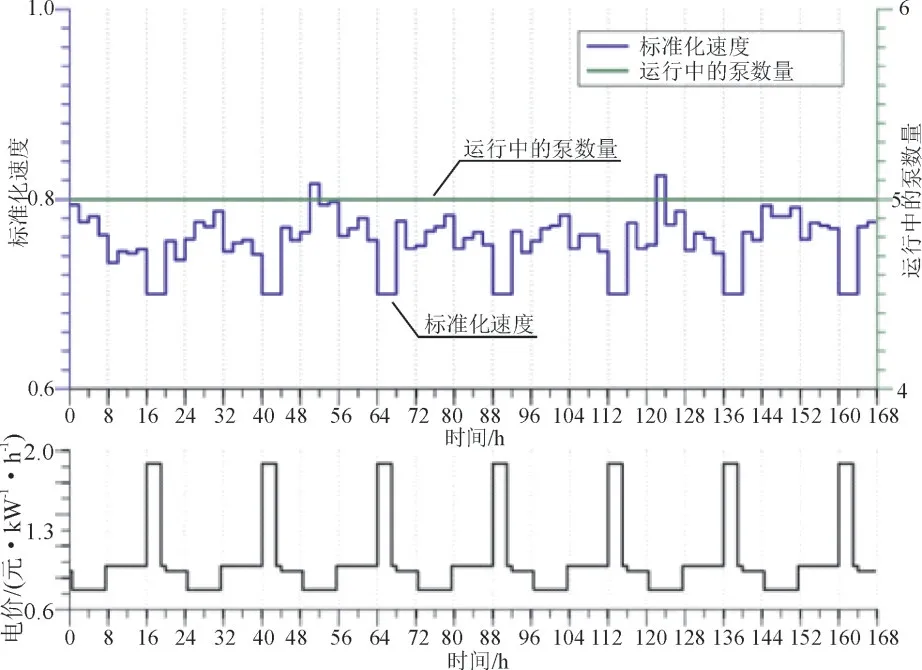
图3 泵站运行随时间的变化情况

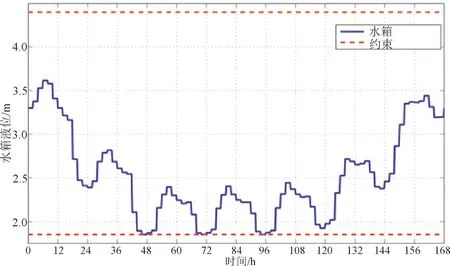
图4 水箱液位轨迹

4 结论

泵的运行优化是一项艰巨的任务，因为它具有显著的复杂性和不一致性。在本文中，同时对泵和阀进行优化。优化模型是通过GAMS 语言从EPA⁃NET格式的水力模型和描述运行约束、电价和泵站配置的附加文件中自动生成的。为了减小优化问题的规模，使用模型简化算法来简化模型，将非线性规划求解器CONOPT 应用于解决连续优化问题，随后，使用简单的试探法将时间序列转换为混合整数形式。

将该方法应用于一个大规模的WDN，考虑到WDN 复杂的结构、泵站之间的相互作用、不同的层位、时间步长、操作约束以及水力模型的拓扑变化，在几个情景下进行模拟，证明了该方法具有能自动生成方案的优点并且具有解决各种优化问题的能力。建议下一步的工作是改进当前的离散化算法。