基于煤质约束优化的多目标配煤方法研究

2021-05-06李晓辰张豪庆张闻中茅大钧

青海电力 2021年1期

朱震，胡涛，李晓辰，张豪庆，张闻中，茅大钧

(1.华能国际电力股份有限公司上海石洞第二电厂，上海 200942；2. 上海电力大学自动化工程学院，上海 200090)

0 引言

随着我国经济和社会的不断发展，对电力的需求急速增加，与此同时也带来火电燃煤需求的大幅度增加〔1〕。但是由于煤炭资源分布不均衡和供需受到季节影响，大多燃煤电厂燃用混合的非设计煤种，配煤掺烧成为目前电厂动力配煤研究的热点话题〔2-3〕。

对于燃煤电厂，长期使用煤质偏离设计煤种的燃煤会使得机组存在运行不稳定、发电效率低下和污染物排放超标等问题，所以近些年来，很多人对配煤掺烧技术进行深入研究。文献〔1〕利用线性加权法预测混煤煤质特性，根据动力配煤约束条件建立以混煤价格最低为目标函数的配煤模型〔4〕。文献〔2〕建立以掺烧煤成本最低为目标函数和煤质成分为约束条件，使用粒子群优化遗传算法进行配煤模型的求解，得到了较好的效果〔5〕。文献〔3〕考虑安全、经济和环保因素，采用多目标粒子群优化方法得到合理配煤比例〔6〕。虽然取得一定成果，但是仍然存在单目标动力配煤模型考虑不全面、惩罚函数难构造和多目标优化算法约束条件难处理等问题，导致目前配煤方法缺少可靠性和应用价值〔7〕。

针对上海某电厂实际混煤数据进行分析，根据各单煤煤质与混煤煤质的关系，采用支持向量机建立混煤煤质预测模型，并对煤质约束条件进行优化，使用CW算法建立群体进化配煤模型，根据实际情况选择最优的配煤方案。改变其原有的按照人工经验配煤的方式，为发电企业在配煤方案上提供指导意见。

1 基于支持向量机的煤质预测模型

优化动力配煤的前提是建立混煤煤质预测模型，确定各单煤不同成分指标及配比与混煤之间的关系。一般认为存在线性加权关系，但是实际上存在很大偏差〔8〕。

支持向量机(Support Vector Machine, SVM)是一种解决非线性问题的有效方法，合理利用核函数可以学习输入与输出之间的关系，对由于混煤煤种复杂多变的小样本数据具有很好的分析能力和适用性〔9-10〕。利用支持向量机预测混煤煤质中非线性成分，可以提高配煤准确性。

假定输入xi和输出yi的训练样本集：

T={(x1,y1),(x2,y2),…,(xn,yn) }

(1)

f(x)=WTx+b

(2)

式中：WT为权重向量；b为偏置常数。

经过一系列的映射转换，将非线性变量映射到高维特征空间中，并利用核函数K(xi,xj)建立线性回归模型：

(3)

(4)

式中：αi,αi*为不同约束条件的拉格朗日乘数，采用径向基核函数。

2 基于约束优化的多目标配煤模型

2.1 优化指标选取

配煤模型中包含煤质特性和燃烧特性参数，考虑到燃烧属于滞后过程，可以根据实时状态判断机组燃烧特性，通过调整弥补配煤方案中的误差影响，并且混煤煤质与设计煤种之间的差异可以影响机组的燃烧特性，所以结合煤价和煤质特性参数提出经济性指标和约束性指标作为优化指标〔11〕。既可以通过煤质指标控制混煤的燃烧特性，又可以降低算法复杂程度，因此这种方法是可行的。

2.2 煤质约束优化

大多配煤模型都是以经济性为目标函数的单目标约束条件问题，但是随着约束条件个数的增加，算法难度也明显增大〔12〕。惩罚函数法是经典的约束处理方法，主要原理是根据约束违反程度的不同构造惩罚项。利用惩罚思想，可以将约束条件构造为惩罚函数使其成为新的目标函数，利用多目标优化算法进行求解，达到两个目标之间的均衡。

约束条件中的煤质特性参数包括发热量(Qad)、硫分(Sad)、灰分(Aad)、挥发分(Vad)和水分(Mad)。具体建立过程如下：

根据电厂锅炉设计标准，配煤模型约束条件可以表示为：

subject to:Mi-δi≤si(x)≤Mi+δi

(5)

式中：si(x)、Mi、δi表示混煤煤质发热量、硫分、灰分、挥发分和水分预测值、设计值和容忍值。

一个个体违反约束条件程度可表示为：

Wi(x)=max{0,|ti(x)-Di|-δi},i=1,2,3,4,5

(6)

由于各个煤质指标差值数量级不同，所以为其设置不同的参数，煤质约束指标为：

(7)

当混煤煤质发热量、硫分、灰分、挥发分和水分都在约束范围内时，CV(x)=0；否则CV(x)的值会随着混煤成分偏离程度增加而增大。

2.3 目标函数构建

电厂进行配煤掺烧的主要目的是追求经济效益最大化，所以非常重视混煤价格，对其建立经济目标函数为〔13〕：

(8)

式中：γ为经济系数；Xj为第j种煤的混配比例；Pj为第j种煤的价格；n为单煤数。

为了保证混煤不会影响锅炉设备的安全运行和环保排放，混煤煤质成分应满足锅炉设计煤种的要求，建立约束目标函数：

(9)

式中：βi代表混煤发热量、水分、灰分、挥发分和硫分的差值标准化系数。

3 进化算法

蔡自兴和王勇在2006年提出一种多目标进化算法：CW算法，包括群体进化模型和不可行解存档与替换机制，可以很好地处理经过约束优化后的多目标配煤问题。

3.1 编码及参数设定

由于配煤模型的特殊性，采用实数编码方法，确定以三种单煤混合的形式，遗传算子前6位进行选择、交叉和变异操作，其中前3位是煤库中随机三种单煤编号，后三位是对应的掺烧比例，根据实际情况将变量范围定义为：min{1,1,1,10,10,10}；max{10,10,10,90,90,90}，并且3种单煤掺烧比例之和为1。

为了平衡两个指标之间的影响，设置了经济系数，可以大大增加算法在寻优过程中的效率和灵活性。为了可以灵活约束煤质成分，设置不同的标准化系数让混煤达到配煤人员的偏好值，进而更好的选择混煤方案。

3.2 CW算法流程

CW算法〔14〕中群体进化模型的步骤为：

首先从由NP个个体所组成的群体Q中随机选择出ε个个体，对其进行选择、交叉和变异等进化操作从而产生ζ个后代，经过计算确定后代中的非劣个体，并随意选择一个非劣个体θ1，假设ε个个体中有l个个体被θ1Pareto支配，当l≥0时，使用θ1随机替换一个被支配的个体，由于ε是小于NP的，所以群体进化会朝着一种稳定状态进行，通过使用非劣个体替代被支配的个体，可以减少结果中无意义解的数量，提高群体个体的整体进化效果。

由于约束目标函数的存在，结果会出现不可行解，CW算法可以对不可行解进行存档并使用替换机制解决问题，具体操作如下：

如果ζ个个体中存在超过约束条件的个体，即不可行解，则挑选出其中约束条件违反程度最小的解，记为x′，且令A=A∪x′，A代表一个档案。

如果mod(gen,m′ )=0，则从A中随机挑选n′个个体，并将n′个个体随机替换群体Q中数量相同的个体。

式中：gen代表进化代数，m′代表每隔m′代执行一次替换操作，n′代表替换的个体数目。

不可行解存档和替换机制可以使不满足约束条件的个体也可以进行替换操作，使群体更快的进入可行域，加快算法寻优速率。

4 实例分析

对上海某电厂锅炉进行动力配煤研究，锅炉设计煤种煤质情况如表1所示，选取实际10中存煤数据进行混配，如表2所示。

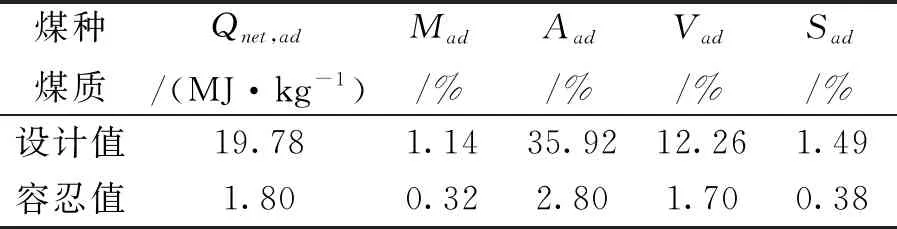
表1 设计煤种煤质

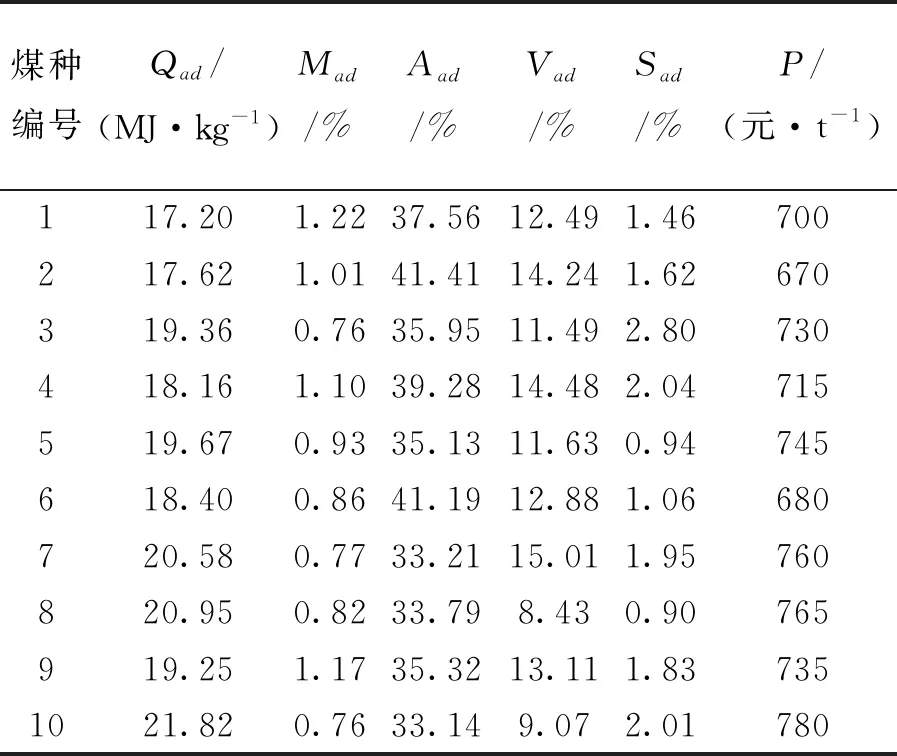
表2 存煤数据库

根据电厂实验得出：混煤挥发分和灰分数据具有非线性，而发热量、水分和硫分具有线性可加性，由于发热量与煤的工业分析有关，并且是煤炭价格的主要影响因素，所以电厂非常重视，故采用SVM和BP神经网络对非线性成分和发热量进行混煤预测。

根据表2数据，随机将3种不同比例的单煤进行混配，将各单煤发热量、挥发分、灰分数据和各自比例一共6个变量作为模型输入，混煤后的数据作为模型输出结果，建立预测模型，将样本数据中350组为训练集，剩余10组数据作为验证集，预测结果如图1所示，不同算法结果的均值误差对比见表3。

表3 算法结果均值误差对比

由图表可以看出，SVM比BP神经网络的均值误差小，达到了预测效果，为多目标群体进化算法建立了良好的预测模型。

采用约束优化的多目标配煤模型确定合适的配煤方案，在没有特定需求的情况下，尽量赋予目标函数同等权重，γ取0.002，为了区分约束反馈，对不同的混煤成分赋予不同的权重，β1、β2、β3、β4、β5分别取0.2、1、0.1、0.13、0.9。种群规模设置为100，迭代次数为200，进行仿真计算后的个体解集分布如图2所示。

经过模型得到的解分布较为规整，约束优化降低了多目标优化算法结果太多难以挑选的问题，列出部分符合条件的个体如表4所示。

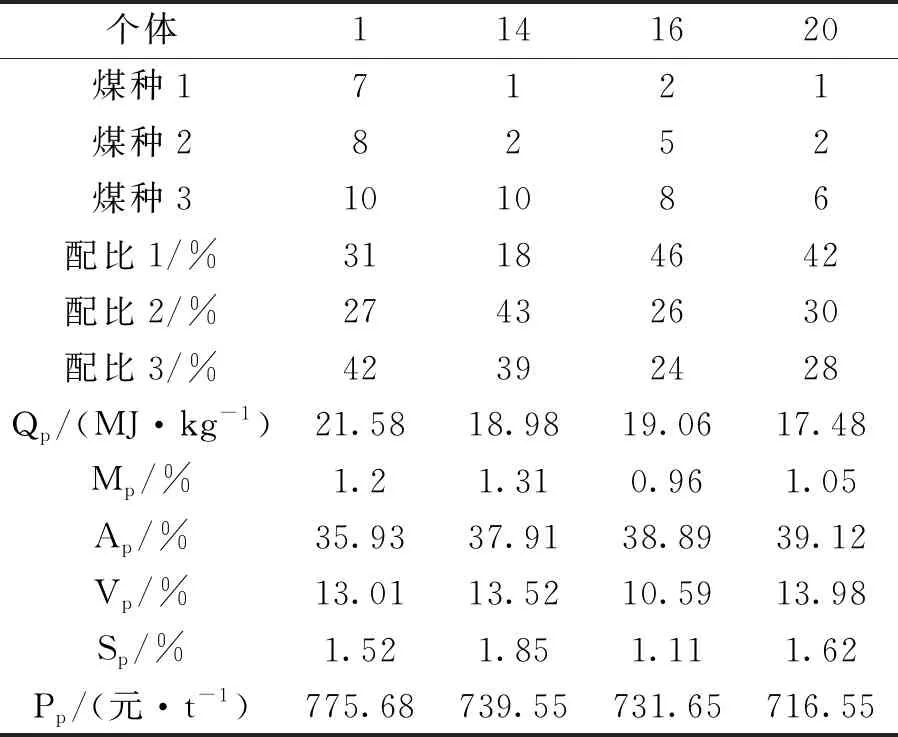
表4 部分个体解集

由图2得，约束优化后采用CW算法可以明确反映个体最重要的信息，当混煤成分均满足约束条件时，横坐标为0，此时分布在y轴上的个体为可行解，当追求混煤成本最低的可行解时，选择个体14,；除了可行解，还可以反映具有最小约束违反程度的不可行个体15和具有最小经济目标函数的不可行个体20，当不考虑约束只追求经济性时，选择个体20；当追求混煤发热量最高时，选择个体1；当追求硫分最低时，选择个体16。配煤人员可以根据实际情况调整模型中的参数克服燃煤煤种复杂多变的情况，增加模型的适用性和配煤灵活性〔15〕。