基于改进的神经网络的军械备件需求预测*

贺拥亮

（武警士官学校军械系，杭州 310023）

0 引言

军械备件是为保证军械装备保持良好的技术状态，以应对部队在开展训练、执行任务、战备等条件下出现的突发故障而预存的一定量的零部件。因此，为保证军械装备可以一直处于或快速恢复良好的技术状态，军械应急维修在军械装备保障中起着重要的作用。军械应急维修是指对出现故障的军械装备进行快速换件式修理，使之能够立即恢复良好的技术状态，发挥其战斗力。一般应用于部队开展实战化训练、遂行多样化军事任务等条件下，军械装备实施战时保障，出现故障等突发情况。军械应急维修能力的提高可以有效提高部队战斗力，快速适应多样化任务环境，确保部队圆满完成各项任务。在当前军械装备的系列化、通用化、模块化配置的大背景下，制约军械应急维修保障的瓶颈在于军械备件能否实现精准供应，这就对军械备件的需求预测提出了新的要求［1］。

现有的备件需求预测主要有移动平均法、指数平滑法等方法，这主要针对连续型的备件需求预测。但笔者通过调研发现，部分军械备件在需求上并不是连续的，而是存在着间断性，满足Johnston 提出的间断型需求模式，即相邻两次需求发生的间隔时间大于1.25 倍的观测周期［2］。因此，传统的连续型备件需求预测方法对此并不适用。

本文提出一种基于改进的神经网络的军械备件需求预测方法，利用神经网络对任意非线性函数的拟合能力，将间断的军械备件需求预测转换成两步：一是需求发生序列预测，由于需求发生序列为间断型，将其转换成连续型后，通过神经网络对需求发生序列进行预测；二是需求量序列预测，将实际需求量转换成需求量序列，应为一连续序列，直接运用神经网络对其拟合预测，得出新的需求量预测。最后，将需求发生序列与需求量序列两者整合后，得出最终的备件需求预测值。

1 改进的神经网络预测模型

神经网络对于非线性的函数拟合效果是比较好的，可以说有足够的数据支撑训练，神经网络可以以任意精度无限逼近一个非线性函数［3］。军械备件需求量正是一个受多个因素影响的非线性函数，可以尝试用神经网络模型进行预测。

神经网络一般由输入层、隐藏层和输出层组成，利用训练样本，经过输入层、隐藏层的传递计算，不断修正误差，得出输出层。同时，可将输出层与样本中剩余数据进行对比，反向修正计算过程，直至输出层符合期望误差，基本计算流程如图1 所示。

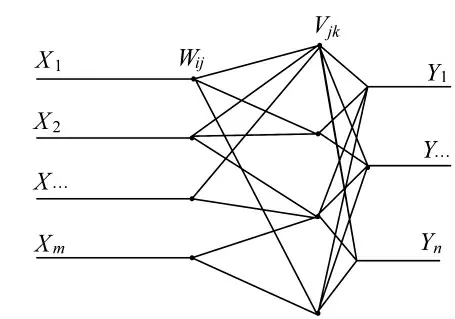
图1 神经网络结构图

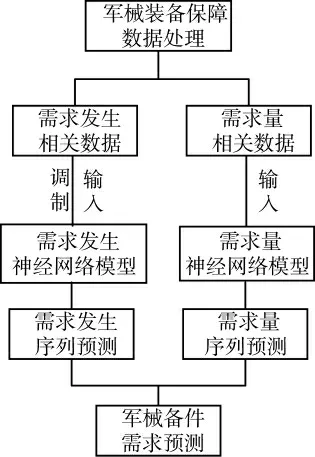
图2 改进的神经网络预测步骤

在进行数据处理时，军械备件出现间断需求的特征：在一个观测周期内，军械备件需求量多次出现了“相邻两次需求发生的间隔时间大于1.25 倍的观测周期［2］”的情况，符合间断需求的特征。而未改进的神经网络预测模型若需同时预测需求发生时间和需求量，则需要大量的装备保障数据作为训练样本，一方面对于数据处理难度增大，另一方面对于部分新装备的备件需求预测难以进行。为此将军械备件需求预测分为需求发生序列预测与需求量序列预测两步，其步骤如图2 所示。

1）军械装备保障数据处理：将历年收集的军械装备保障数据进行处理，在一个观测周期内，分为需求发生相关数据与需求量相关数据两类。

2）神经网络模型建立：仍利用神经网络模型强大的非线性函数拟合能力，对需求发生和需求量进行预测。由于需求发生为不连续数据，在输入时需进行调制处理，得到连续值进行输入。

3）序列预测的输出：经过样本训练与判定，分别得到需求发生序列和需求量序列预测。

4）得出军械备件需求预测：综合需求发生序列与需求量序列预测，得到军械备件需求预测。具体数据处理与函数选择见第2 节、第3 节。

2 需求发生序列预测

2.1 备件发生序列

由于军械备件的需求存在间断性，为了对需求发生序列进行预测，首先需要对实际备件需求进行转换，转换成需求发生时间序列。此时，选用Croston方法［4］提取需求发生序列。

将备件实际需求转换成0-1 发生序列F，如式（1）所示

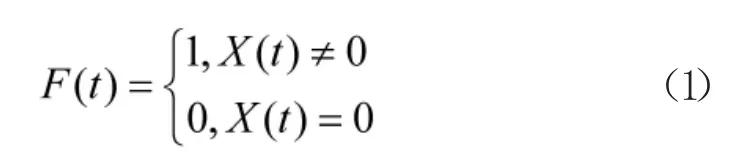
式中，X（t）为备件实际需求。

2.2 备件发生序列调制处理

转换得到的备件发生序列F，由于存在多个断点，无法应用神经网络进行预测，需对基进行平滑连续处理。在此，可借鉴数字调制技术，将F 累加到载波上，既能保持备件实际需求的原始信息，亦能得到备件发生序列的平滑连续信号。正弦信号由于形式简单，调制、解调相对简单，载波一般选用正弦信号对备件发生序列进行调制［5］。

2.3 备件发生序列预测

以完整波形作为神经网络的输入，输出下一个波形的前两个值作为输出层。每个载波波形有6 个离散点，输入层为6 n，其中，n 为正整数，一般隐藏层节点数为3 时，即可任意拟合一个复杂的非线性函数。具体验证结果见第4 节。

3 需求量序列预测

经过上一步需求发生时间序列的转换，需求量序列中转换成需求量，即可得到连续平滑的需求量序列。为有效利用神经网络进行预测，需对输入层进行合理的设计。

一般来讲，军械备件的需求量主要和军械备件的使用、保管、维修等基本信息有关，因此，在选取输入层时，着重考虑相关因素。通过对部队的调研了解，结合历年军械保障的相关数年信息，经过分析，总结出影响军械备件需求量的主要因素有：

2）执行重大任务和参与演练的次数。执行重大任务和参与演练时动用的军械装备与平时训练时情况会有较大差别，由于在执行重大任务和参与演练时，军械装备使用强度大，会对军械装备造成一定的影响。因此，直接将执行重大任务和参与演练的次数之和作为一个影响因子。

3）保障的装备数量。装备数量的不同对备件需求亦不同，总的保障数量基数发生变化，对需求结果影响较为直接。

4）上一周期备件使用量。备件使用有一定的寿命周期，上一周期刚进行更换过后备件不易发生故障，因此，将上一周备件使用量也纳入到备件需求预测中。

备件需求量主要由以上因素决定，故输入层确定为4 个，隐藏层节点仍选3 个进行拟合，输出层为1 个，即备件需求量的预测值。

4 实验验证

4.1 数据处理

提取某单位近年的某军械装备应急保障中的相关资料，作为样本进行分析，检验该神经网络预测模型的适用性。由于应急保障资料繁多，为防止样本数据突变，影响神经网络预测结果，在提取样本时，设定了本实验的前提条件：

1）应急维修具有一定的突发性，应综合考量备件的需求情况，备件需求量在预测时以月为观测周期；

2）装备数量按该单位正常编制军械装备数量，挑选样本时，动用数量少于总数量的30 %不统计在内。

军械备件需求序列实例如下页表1 所示。

根据前文所述的数据处理方法，将军械备件需求实例，按要求转换成备件发生序列和备件需求量序列，分别如表2、表3 所示。

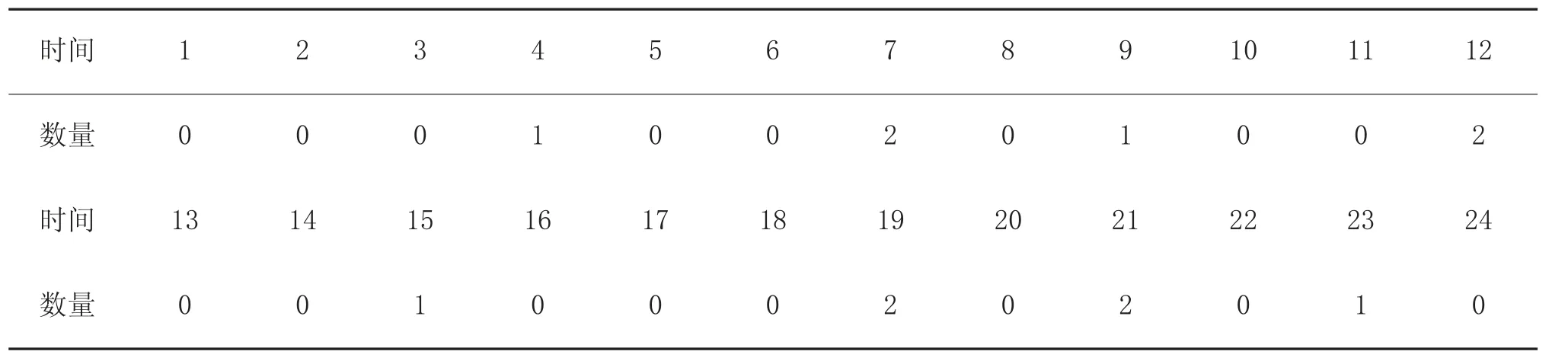
表1 军械备件需求序列实例

表2 军械备件发生序列

表3 军械备件需求量序列

4.2 需求发生序列验证

将需求发生序列经过载波调制，可得到连续平滑的需求发生序列。如图3 所示。

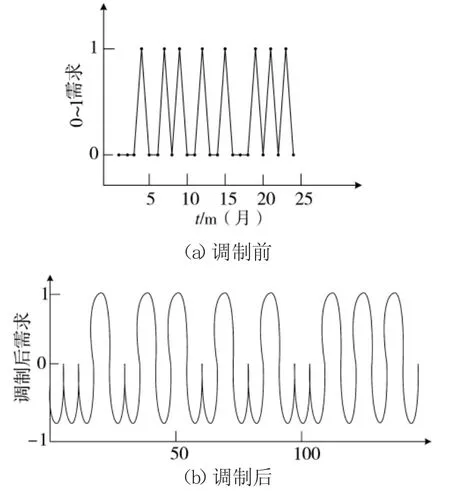
图3 需求发生序列

根据调制后的需求发生序列，采用神经网络模型进行预测。通过大量实验及比较确定：输入层节点数24，隐层传递函数为tansig，输出层传递函数为purelin，用总体数据的4/5 作为训练数据，1/5 作为测试数据进行预测。

为验证预测精度，选用式（5）作为需求发生序列的预测精度计算：

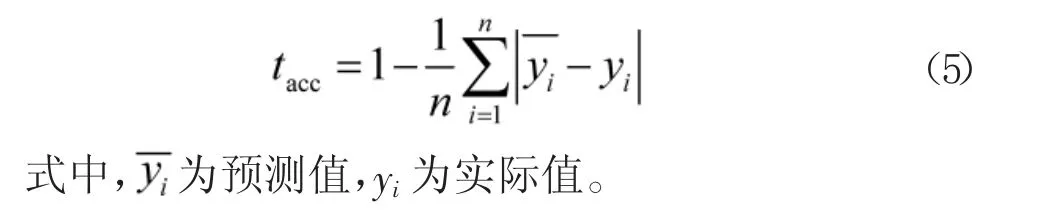
经过计算，得到备件需求发生序列的预测精度如表4 所示。

表4 备件需求发生序列预测精度

从预测精度来看，采用正弦波调制后的预测方法符合预期。同时为进一步检测该预测有效性，采用文献［21］的方法，另选择二次函数、高斯函数以及墨西哥草帽小波函数等几个常用的载波函数分别进行了试验，其精度均不及正弦函数。

预测结果如图4 所示。

图4 备件需求发生序列预测

4.3 备件需求量序列验证

根据第3 节设定的相关要求，从保障数据中提取训练样本，遇0 值时，相关数据叠加至下一周期，如表5 所示。

表5 备件需求量训练样本

根据训练样本数据，采用神经网络模型进行预测。通过大量实验及比较确定：输入层节点数4，隐层传递函数为tansig，输出层传递函数为purelin，用总体数据的4/5 作为训练数据，1/5 作为测试数据进行预测。

为验证预测精度，选用式（6）作为需求量序列的预测误差计算：

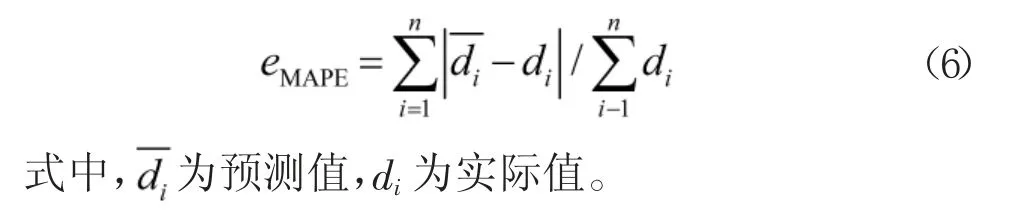
经过计算，得到备件需求量序列的预测精度。同时与文献［5］提供的指数平滑法、Croston 方法等备件预测方法进行对比来看，其预测误差如表6 所示。

从预测精度来看，改进的神经网络方法预测误差基本控制在60%左右，与指数平滑法、Croston 方法相比，其预测误差要小很多，因此，证明本文提出的改进的神经网络预测方法是有效的［22-23］。

综合备件需求发生预测和备件需求量预测的结果，可得出实际备件的需求量预测结果，如图5所示。

5 结论

本文为了解决当前军械应急维修过程中备件需求问题，在对军械备件需求分析过程中判定为间断性需求，若直接采用神经网络的预测方法，数据处理难度大，且预测精度不高、误差较大，对新装备而言，由于训练样本少，更是难以进行需求预测。为此，将军械备件需求预测划分为两步：一是需求发生序列预测，将间断型的时间序列经过正弦函数调制成连续序列，仍利用神经网络模型的强大非线性拟合能力，得出需求发生序列；二是需求量序列预测，综合考量装备保障数据，选取训练时长、执行重大任务和参与演练的次数、保障的装备数量和上一周期备件使用量4 个因子作为需求量序列预测的输入层，输入神经网络模型进行预测，得出需求量序列。

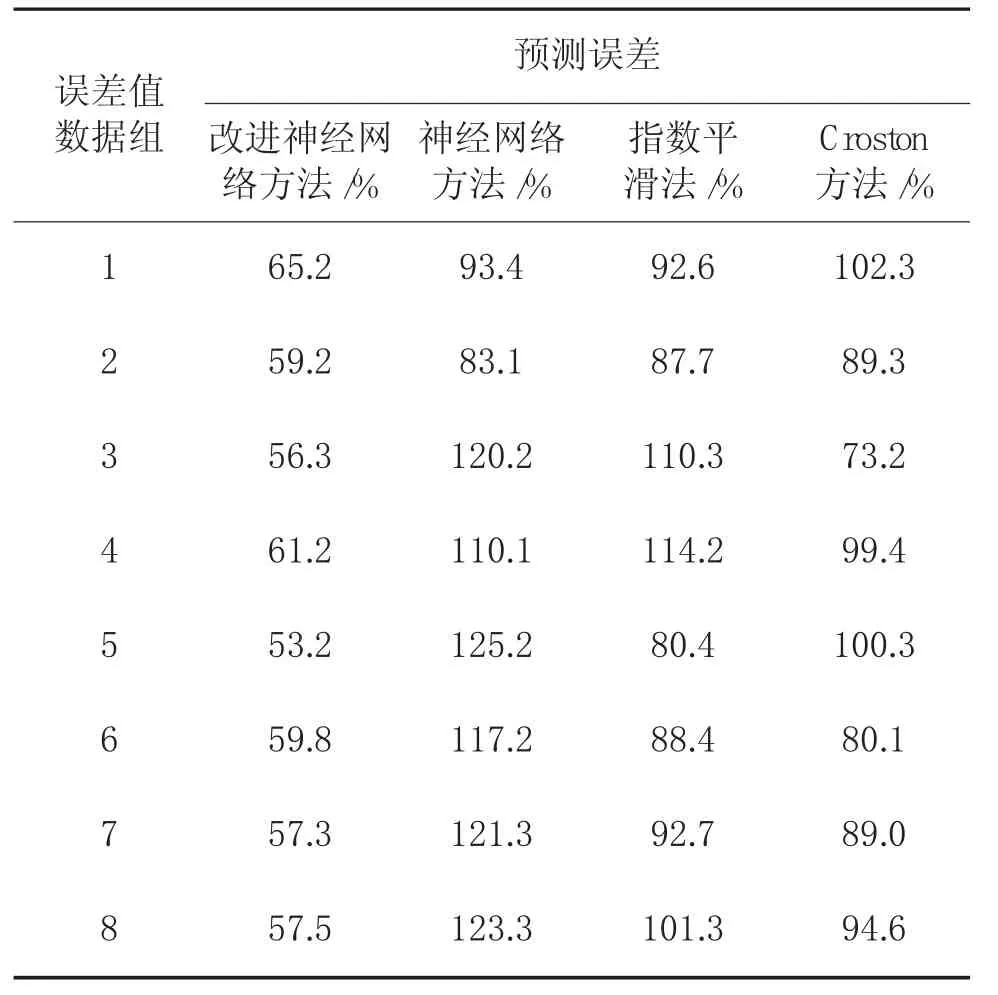
表6 备件需求量序列预测误差

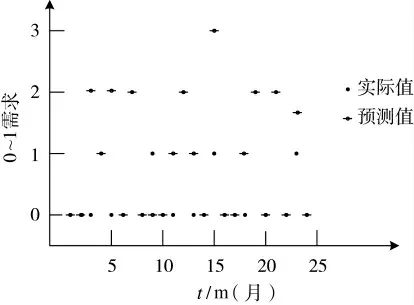
图5 备件需求预测值

最后，结合某部队装备保障数据，按改进的神经网络模型预测步骤进行预测计算，得出了军械备件需求预测。实验结果表明，该方法可以有效地对军械应急维修下的备件需求作出预测，与直接应用神经网络预测方法、指数平滑法、Croston 方法等相比，其在预测精度上有较大提高，基于改进的神经网络军械备件需求的预测可以为下步军械应急保障提供依据。