基于MPS 方法的减速器齿轮搅油损失分析

张志行，朱波，张世宇，江宇孝，韦邦暄，胡岳伟

（1.230009 安徽省 合肥市 合肥工业大学 汽车与交通工程学院；2.230000 安徽省 合肥市 合肥工业大学 汽车工程技术研究院）

0 引言

减速器是车辆动力传动系统中的关键部件，其在工作过程中产生的功率损耗势必会降低动力传动系统的传递效率，从而使整车动力传递路线效率降低，油耗增加。根据相关研究，减速器功率损失降低1 kW，可减少相当于4 kW 能量的燃料使用量[1]。飞溅润滑是减速器内最常用的润滑方式，在该润滑方式下，功率的损失分为有载功率损失和无载功率损失。车辆在正常行驶条件下，减速器内齿轮传动系统工作于高速低载状态，以齿轮搅油损失为代表的无载功率损失为主，因此，研究减速器内齿轮搅油损失对提高整车传动效率和燃油经济性有着重要意义。

齿轮搅油功率损耗来源于齿轮转动时克服润滑油的黏性阻力，主要与齿轮的几何参数、工作参数与运动参数有关，其研究方法主要包括理论分析、实验研究和数值仿真。由于变速器内润滑油与空气形成的油气混合物流体动力特性复杂、温度分布不均匀、润滑油密度等主要参数变化不规律，直接采用理论研究方法较为困难[2]，目前国内外大多采用实验方法，通过拟合大量实验数据以得到经验或半经验的搅油损失功率计算公式。Terekhov 的研究表明，搅油功率损失取决于润滑油流动状态，并且随着齿轮旋转速度和齿轮浸入深度的增加而增加；Boness 提出了层流、过渡和湍流3 种不同状态下齿轮搅油功率损失的经验公式；梁文宏[3-5]使用Fluent 软件进行搅油损失仿真，研究表明，随着转速、齿轮浸入深度增大，搅油损失会相应增大。

自20 世纪90 年代以来，出现了无网格数值计算的求解方法，该方法避免了复杂的网格操作，具有独特的优势。其中具有代表性的是MPS（Moving Particle Semi-implicit）方法，通过跟踪多阶离散化粒子模拟流体的流动，可实现对泼溅、自由液面流动等复杂情况的计算。本文基于无网格化的MPS 方法，利用Particleworks 软件对某电动汽车的二级减速器进行搅油损失仿真计算。

1 MPS 方法

1.1 基本原理

MPS（Moving Particle Semi-implicit)，移 动粒子半隐式法，是由日本的Koshizuka 等学者于1995 年提出的一种可用于求解模拟不可压缩液体流动问题数值计算方法，该方法基于拉格朗日控制法、采用粒子离散化连续介质力学的思想，对多维粒子运动进行追踪模拟。MPS 最显著的特点是不必对仿真的各物体进行繁琐网格划分，避免了数值仿真中由于网格变形引起的计算失真，并且在相同条件下使用基于MPS方法的CFD软件，大大缩短了计算时间。

MPS 的基本原理是用一群粒子替代计算域中的流体，利用拉格朗日方程求解不同粒子在不同时刻下的流动坐标，再根据相互作用关系求解基本流动方程。同时，基于粒子间的耦合关系，可不断对粒子的上一时刻的流动情况和下一时刻的流动情况进行修正和模拟，随着时间步的推进与迭代次数的增加，即可准确获得整个流体的动态流动信息[6]。

1.2 数学模型

1.2.1 控制方程

MPS 法的基本控制方程是连续方程和Navier-Stokes 方程。

连续方程（质量守恒定律）

式中：ρ——密度；u——速度；P——压力；v——运动粘度系数；g ——重力加速度。

1.2.2 粒子相互作用数学模型

MPS 方法中，粒子运动具有极强的随机性，所以，需要在每个时间步中构建新粒子的计算模型以离散方程，各个粒子均考虑其不同时间步下的速度、压力、坐标等物理量，粒子正是通过这些物理量的变化规律进行相互作用，因此，用来离散方程的各种数学模型，实际上都是粒子间的相互作用模型。这些数学模型包括梯度模型、拉普拉斯模型、粒子数密度模型、散度模型、权函数模型等。以上各个数学模型在MPS 方法中的形式如下：

权函数模型

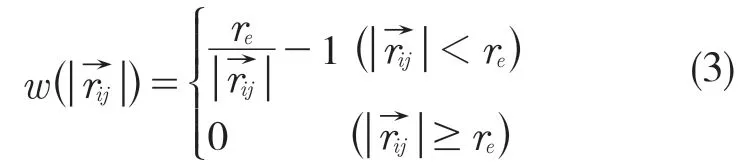
式中：i，j——粒子代号；re——粒子作用的有效半径；——i，j 粒子的距离矢量。权函数用来表示粒子之间的相互作用按照2 个粒子之间的距离加权，是其他作用函数的基础。

权函数曲线如图1 所示。

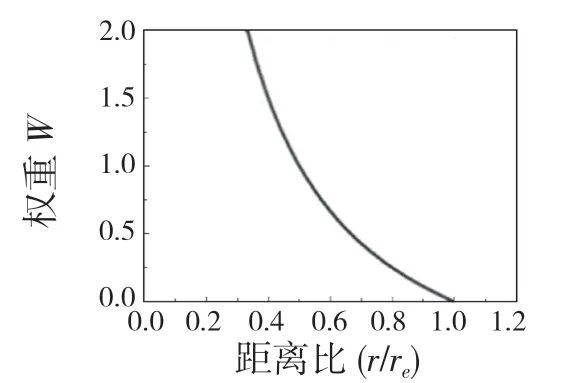
图1 权函数曲线Fig.1 Weight curve

粒子数密度模型

粒子数密度是表示粒子放置密度的无量纲量，是MPS 方法中的特有量。在满足不可压缩条件的粒子放置密度中，粒子数密度是一个固定的值。

粒子相互作用的拉普拉斯模型

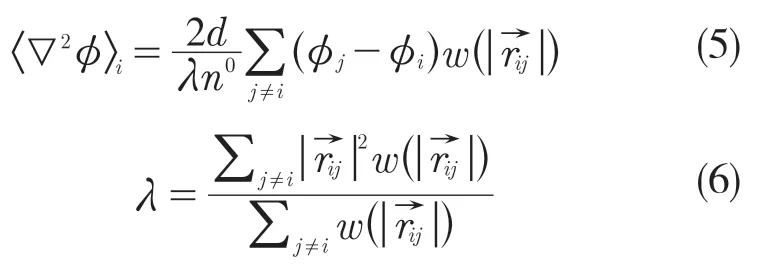
式中：d——求解问题的空间维数；φ——粒子物理参数标量值；n0——粒子数密度初始常值；λ——修正因子。

拉普拉斯模型的原理图如图2 所示。该模型利用权重函数分布在相邻粒子j 之间分配粒子i的一些变量，对导数进行2 阶离散并用于计算粘度和压力。

粒子相互作用的梯度模型

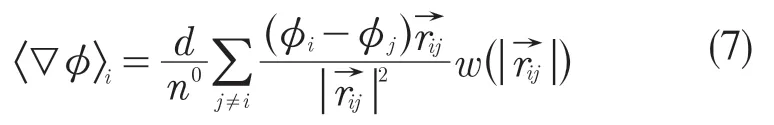
式中：d——求解问题空间维数；φ——粒子物理参数标量值；n0——粒子数密度初始常值。梯度模型对1阶导数进行离散并用于粒子速度修正。

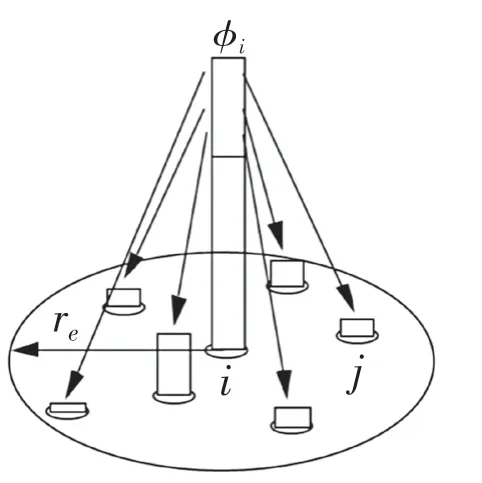
图2 粒子相互作用拉普拉斯模型Fig.2 Laplace model of particle interactions

粒子相互作用的散度模型

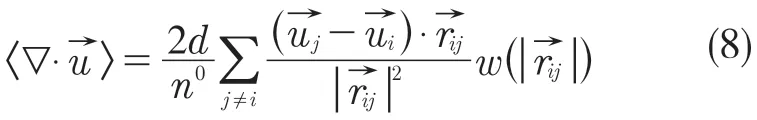
式中：d——求解问题的空间维数；φ——粒子物理参数标量值；n0——粒子数密度初始值。

在散度模型中，通过梯度模型建立对称梯度模型，再利用速度散度计算压力泊松方程的源项。

1.3 MPS 算法

在MPS 方法中，每次计算过程都分为显式和隐式两步。第1 步考虑粒子初始放置情况、重力加速度和边界条件的作用，对粘度项、粒子坐标以及粒子速度进行第1 次显示计算，并计算粒子数密度；第2 步基于已改变的粒子数密度作为初始条件，建立压力泊松方程，通过CG（共轭梯度法）迭代求得压力场后对粒子坐标以及粒子速度进行隐式修正，保证粒子数密度恢复到初始状态以满足不可压缩等约束条件。其中，压力泊松方程形式以及速度计算方程形式如下：

粒子速度显式计算方程

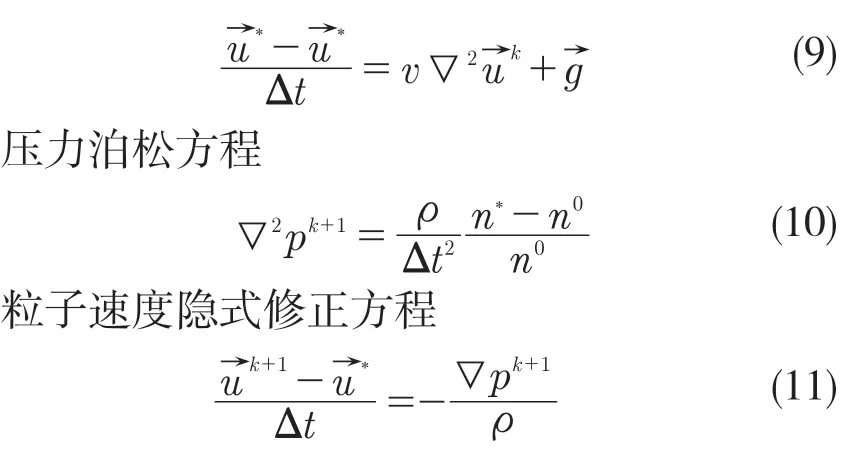
式中：n——粒子数密度；n0——粒子数密度初始常值；k——当前时间步；*——显式计算已经完成阶段的物理量；v——运动粘度系数；P——压力；ρ——密度。

MPS 计算方法整体流程：首先输入计算条件及粒子初始放置条件，通过显式计算方法计算粘度项、模拟粒子运动，之后隐式求解泊松压力方程，基于已求解量显式计算压力梯度项并对速度项和粒子坐标进行修正，根据预设时间步进行迭代计算，最终输出粒子坐标分布。

2 减速器搅油损失MPS 分析

2.1 搅油损失分析

Particleworks 软件是采用MPS 方法的计算机仿真软件，其先进的求解器使用粒子算法，可以较好地对减速器中润滑油复杂的运动情况进行模拟。

齿轮搅油力矩的计算方法在Particleworks 软件内被定义为每个齿轮元素多边形对粒子施加的力的反作用力，其计算步骤一共分为3 个步骤：（1）根据Navier-Stokes 方程，粒子附近和与多边形相互作用的粒子被加速；（2）多边形施加在粒子上的加速度的反应被看作是施加在多边形上的加速度。这被定义为力(x/y/z)；（3）计算力的交叉积和粒子与旋转中心之间的距离矢量。这被定义为扭矩（x/y/z），其示意图如图3 所示。

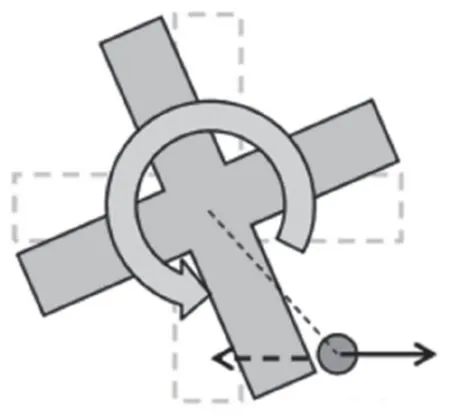
图3 搅油力矩原理示意图Fig.3 Schematic diagram of stirring torque principle

搅油损失功率计算公式

式中：Tloss——齿轮搅油总力矩；N——齿轮转速。

2.2 仿真参数设置及结果分析

根据实际的减速器模型，对减速器的外壳主体结构及内部齿轮进行三维建模，并将相应模型导入到Particleworks 软件中。在车辆行驶的一般工况中，主要是由输出轴齿轮搅动油液对减速器进行飞溅润滑，因此，本次仿真中对输出轴齿轮的搅油损失功率进行分析计算[7]。考虑实际的汽车行驶工况，设输出轴转速为287，405，550，800 r/min 四种情况，输出轴齿轮油液浸入深度分为30，40，50，60 mm 四种情况。润滑油选取85W/90 齿轮油，查阅相关手册，可得润滑油密度ρ=825 kg/m3，运动粘度系数为7×10-6m2/s。其16 种组合情况的搅油损失功率经Particleworks软件仿真分析计算可得。如表1、图4 所示。

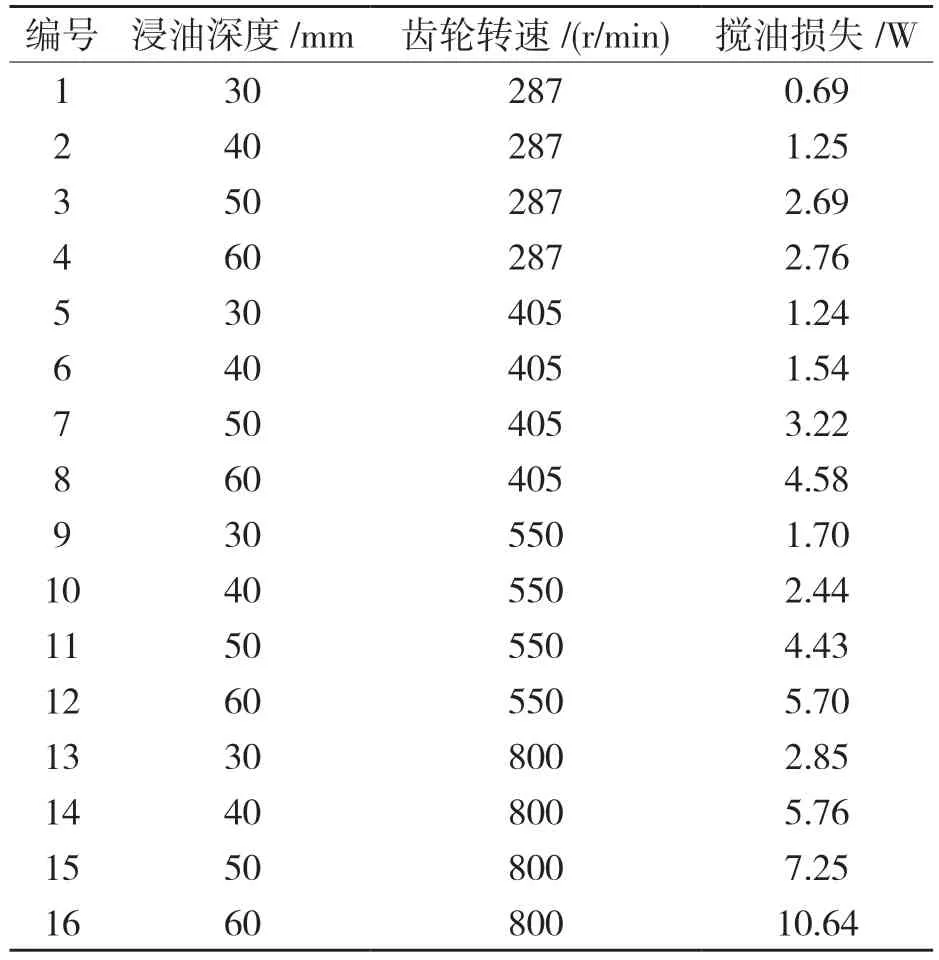
表1 各状态搅油损失分析结果Tab.1 Analysis results of oil loss in each state

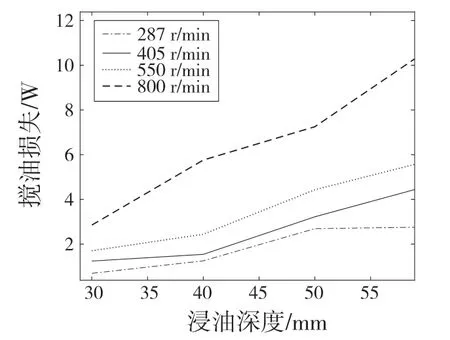
图4 各状态搅油损失分析结果Fig.4 Analysis results of oil loss in each state

根据以上结果可以分析出，随着齿轮浸入油液深度的增加，搅油损失功率相应增加。随着输出轴斜齿轮转速的增加，搅油损失功率也相应增加。且在齿轮转速变化不大的范围中，浸油深度对搅油损失起主要影响。

基于Particleworks 软件，可直观地看到不同状态下减速箱内润滑油的飞溅情况。选取1 s 为时间节点，齿轮搅油飞溅情况如图5 所示。图5（a）中，减速器输出轴转速为287 r/min，从左到右齿轮浸油深度分别为30，40，50，60 mm；图5（b）中，减速器输出轴转速为405 r/min，从左到右齿轮浸油深度分别为30，40，50，60 mm；图5（c）中，减速器输出轴转速为550 r/min，从左到右齿轮浸油深度分别为30，40，50，60 mm；图5（d）中，减速器输出轴转速为800 r/min，从左到右齿轮浸油深度分别为30，40，50，60 mm。分析得出，随着齿轮浸油深度的增加、齿轮转速的提高，输出轴斜齿轮搅动油量越多，润滑油飞溅量越多。

图5 Particleworks 齿轮搅油模拟仿真结果Fig.5 Simulation results of Particleworks gear oil churn

3 结论

本文详细阐述了MPS 方法的算法原理与粒子相互作用数学模型。针对电动汽车传动系统无载功耗特性，将MPS 方法创新性地应用于减速器齿轮搅油损失分析中，利用基于无网格划分的粒子追踪软件Particleworks 进行模拟仿真，结果表明，齿轮随着浸油深度、齿轮转速增加，搅油损失功率也不断增加，验证了MPS 方法在减速器搅油损失分析的可行性。