城市道路混合交通流道路交叉口信号配时优化方法

徐琛辉，马明辉，王栋

（202004 上海市 上海工程技术大学 机械与汽车工程学院）

0 引言

城市道路交叉口交通运行往往呈现明显的混合流特性，所以结合我国城市道路现状，在混行交通条件下对城市道路平面交叉口进行科学、合理的信号优化，对于改善城市道路拥挤状况、提高道路通行能力、减少交通事故具有十分重要的现实意义。

目前，国内外学者针对交通数据处理的研究主要集中在对历史交通数据中异常数据的处理方面。国外学者偏好单一交通流的微观仿真，对配时优化方案的研究居多，对混行交叉口多种交通量的综合研究较少，如Mina Ghanbarikarekani[1]，Nasser R[2]，Lin Tong[3]等人进行的有关研究；而国内研究大多能从宏观角度出发，统筹混行交叉口的运行状况来进行相关研究，符合我国道路交叉口的实际情况，如江航[4]、甘杨杰[5]、张永志[6]、陈海洋[7]等人进行的研究。

综上所述，本文拟考虑到我国实际道路交通状况，针对混行交通流环境下城市道路交叉口信号优化问题，考虑机动车流、非机动车流及行人流等要素，以提升交叉口交通运行效率为出发点，采用最佳信号周期及流量比的优化方法。采用机动车—非机动车—行人3 种交通流的配时优化方案具有创新性和可行性。

1 问题描述

本文依据混行交通流特性和传统Webster 配时法设计信号配时优化设计。（1）以最佳信号周期和绿灯时间分配为优化目标，建立优化配时理论；（2）以三相位和四相位的十字型混合交通流道路交叉口为仿真背景，分别进行优化配时理论和传统Webster 理论的仿真模拟对比，并做出合理评价。

2 考虑混行交通的信号配时优化方法

2.1 交叉口信号配时流程

交叉口信号配时过程以总损失时间L、最佳信号周期C0、总有效绿灯时间Gei及各相位有效时间gei的计算顺序构成，具体流程如图1 所示。

图1 信号配时流程图Fig.1 Signal timing flow chart

2.2 最佳信号周期优化模型

以米勒延误公式替代Webster 延误公式

式中：Q0——平均过饱和排队车辆数；c——周期时长，s；q——到达率，pcu/h；λ——绿信比；x——饱和度。

然后引入新变量完全停车率

式中：h——每小时完全停车数；y——流量比。建立停车与延误关系函数PI

式中：K——停车补偿系数；D——总延误时间（s）。当PI 最小时

其中，停车补偿系数可根据具体目标选择，具体取值如表1 所示。

表1 停车补偿系数选择Tab.1 Selection of parking compensation coefficients

本文要求延误时间尽可能减少，故K 取值为0，因此优化后的最佳信号周期公式为

2.3 绿灯时间分配模型

在我国实际道路运行情况中，非机动车和行人的流量占比不容忽视，因此，本文在信号配时过程中将二者引入流量比参数中，以体现混行交通环境下的优化配时。

各相位流量比优化公式为

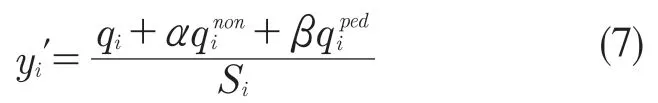
式中：qi——i相位机动车流量（pcu/h）；qinon——i 相位非机动车流量（辆/h）；qiped——i相位行人流量（人/h）；Si——i 相位饱和流量；α——非机动车换算系数；β——行人换算系数。

根据《车型分类及折算系数》，人力三轮车、助动车等非机动车换算成标准车辆数（pcu）时，换算系数取0.2，即α=0.2；行人换算系数可根据非机动车与行人时空比式（8）推算：

式中：m——非机动车与行人换算系数，m=2[5]；s非——非机动车占道面积；s人——行人占道面积；v非——非机动车速度；v人——行人速度。

式（8）得出行人换算系数β=0.1，将yi'代入式（6）可得

3 案例分析

仿真背景基于机动车道、非机动车道及人行道构成的混合道路交叉口，其情况如图2 所示。图中，十字交叉口南北向进口处各有左转、直行及右转三车道及非机动车道；东西向进口处设有左转、直行及直右三车道及非机动车道。机动车道道宽为3.5 m，非机动车道为3 m。各路口交界处设有常规人行横道。

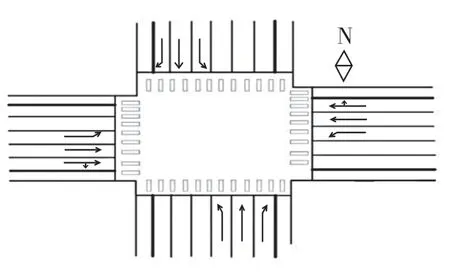
图2 信号配时流程图Fig.2 Road intersection channelization diagram

3.1 实验方案设计

一方面，本文分别进行三相位和四相位的传统Webster 方案配时及优化方案配时的计算；另一方面，本文运用VISSIM 软件的评价模块进行评估，主要分成3 个排队车辆指标（平均排队长度（AVG）、最大排队长度（Max）、排队停车数（Stops））及2 个延误指标（车辆总延误平均值和车均停车延误）。

表2 三相位各进口流量数据Tab.2 Three-phase flow data of each inlet

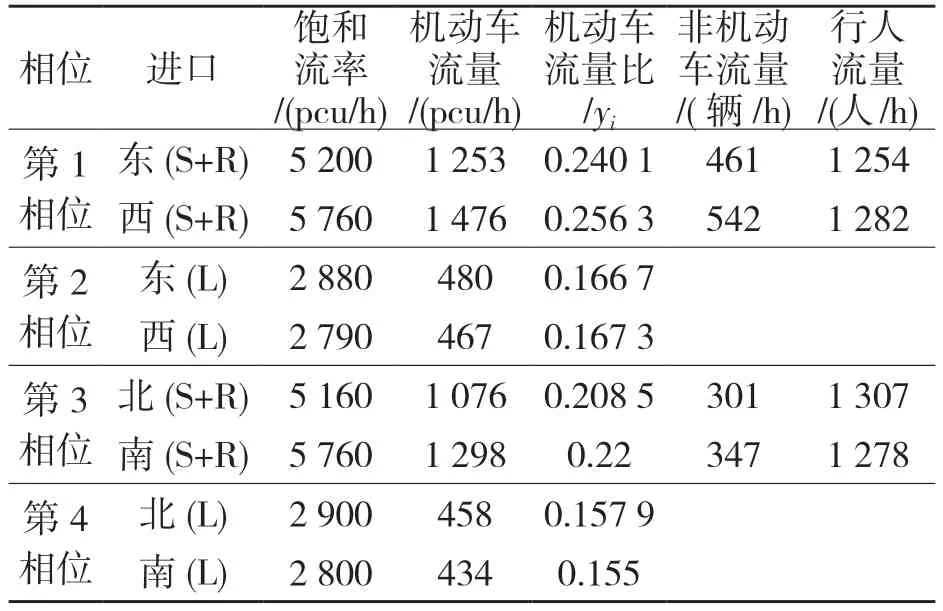
表3 四相位各进口流量数据Tab.3 Four-phase flow data of each inlet

3.2 配时方案优化结果

经计算，三相位传统Webster 法配时图、优化方案配时图如图3、图4 所示；四相位传统Webster 法配时图、优化方案配时图如图5、图6所示。

图3 传统Webster 法三相位配时图Fig.3 Traditional Webster method for three-phase timing diagram

图4 优化方案三相位配时图Fig.4 Three-phase timing diagram of optimization scheme

图5 传统Webster 法四相位配时图Fig.5 Four-phase timing diagram of traditional Webster method

图6 优化方案四相位配时图Fig.6 Four-phase timing diagram of optimization scheme

3.3 实验结果分析

各相位和方法的仿真结果对比见表4、表5。仿真结果表明，三相位的优化配时方案在排队车数和延误上均有改善。其中，三相位排队停车数减少6.9%，车辆总平均延误减少22.8%，车均停车延误减少24.6%；四相位排队停车数减少28.9%，总平均延误减少2.4%，而车均停车延误减少2.1%。

表4 各相位和方法仿真结果的对比（1）Tab.4 Comparison of simulation results of different phases and methods（1）

表5 各相位和方法仿真结果的对比（2）Tab.5 Comparison of simulation results of different phases and methods（2）

综上所述，在混行交通流三相位和四相位交叉口模拟环境下，优化配时方案能降低排队车辆数及延误时间。其中，优化方案对三相位延误时间降低显著，而对四相位排队车辆数降低显著。

4 结论

本研究针对混行交通环境下城市道路交叉口信号配时问题展开研究，对传统Webster 配时方法进行优化。优化后的模型特点为：考虑混行交通流特征，引入非机动车和行人交通流量，并以排队车辆数和延误为最佳目标，对最佳信号周期及绿灯时间分配进行修正。实验结果表明，优化后的配时模型有利于减少排队时间和延误时间对城市道路平面交叉口进行科学、合理的信号优化，对于改善城市道路拥挤状况、提高道路通行能力、减少交通事故具有一定现实意义。