高速列车车轮多边形对齿轮箱疲劳寿命的影响
2021-05-04户攀攀刘建新宋吉超
户攀攀 刘建新 宋吉超
1西南交通大学机械工程学院 成都 610031 2西南交通大学牵引动力国家重点实验室 成都 610031 3柳州铁道职业技术学院 柳州 545616
0 引言
齿轮箱系统是高速列车的关键部件,其发生故障时会直接影响高速列车的正常运行。目前高速列车为追求轻量化,齿轮箱体一般采用轻质铝合金材料铸造结构,但该材料结构在疲劳强度方面存在不足[1]。车轮多边形是高速列车运行过程中常见的磨耗现象,该现象产生时会引起剧烈的轮轨冲击,导致轮轨作用力增大[2]。由于高速列车齿轮箱悬挂方式特殊,极易受到外部激励的影响,因车轮多边形现象而产生的轮轨激励会直接传递到齿轮箱上,使其长期处于异常振动状态。
何斌斌[3]针对高速列车齿轮箱异常振动问题进行研究,简述齿轮箱系统的主要故障形式,分析高速列车的激扰源及其特征,得出引发齿轮箱裂纹的主要原因是车轮不平顺的激扰力激发齿轮箱的固有频率产生共振现象。李广全[4]等对齿轮箱在振动载荷下进行应力分析,得到齿轮箱应力响应强度随列车运行速度的增大而增大,通过对齿轮箱结构疲劳损伤影响参数分析得到不同载荷下齿轮箱疲劳损伤程度。王文静[5]等研究了镟修等对高速列车齿轮箱动应力与等效应力的影响,发现镟修后齿轮箱体的动应力幅值与等效应力均比镟修前显著减小,这是由于镟修消除了车轮高阶多边形,在一定程度上改善了齿轮箱体的受力状态。邹宇航[6]等针对高速列车齿轮箱体开裂问题,进行高速列车齿轮箱线路跟踪试验,得出车轮多边形激励较齿轮箱内部啮合激励对齿轮箱振动的影响更大,箱体的疲劳寿命随着多边形幅值的增大而显著降低。本文利用Simpack动力学软件和Ansys有限元软件,建立了含有齿轮箱支撑轴承的驱动系统以及齿轮箱体有限元模型的刚柔耦合动力学模型,以车轮多边形为输入激励,采用数值仿真分析方法,研究高速列车车轮多边形对齿轮箱疲劳寿命的影响。
1 建立模型
1.1 驱动系统子结构模型
在Simpack 软件中建立驱动系统子结构,采用225号力元来模拟齿轮啮合,该力元可详细描述渐开线齿轮的齿轮接触,齿轮几何外形采用25号齿轮外形参数定义。齿轮箱通过简单力元与构架连接,并通过88号滚动轴承力元与轴连接。输入轴上为两个圆柱滚子轴承和一个球轴承,输出轴上为两个圆锥滚子轴承。如图1所示,以上3种滚动轴承在建模时的参数有:LW为轴承滚子有效长度,D为轴承滚子有效直径,Dpw为轴承节圆直径,α为轴承接触角,ri为保持架内圈半径,ro为保持架外圈半径。采用88号滚动轴承力元可实现轮轨间激励经轴承传递到齿轮箱上,更好的反映齿轮箱的振动状态。
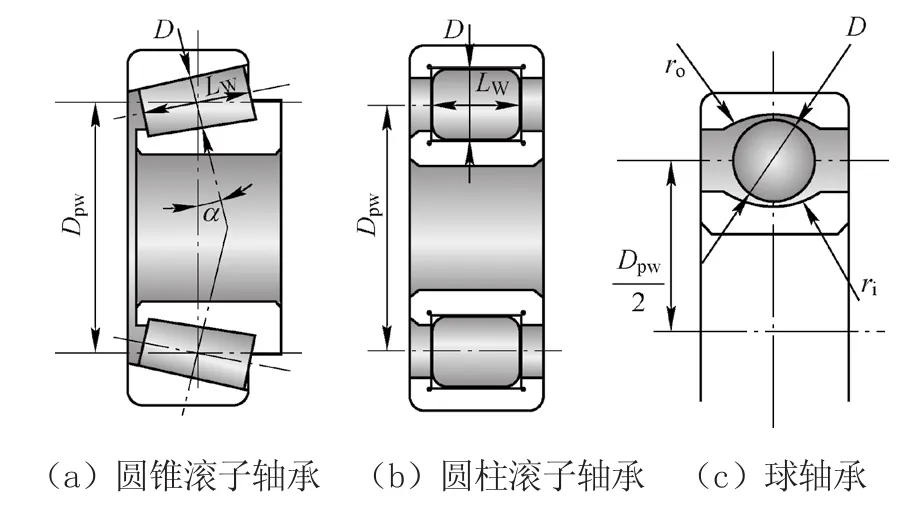
图1 轴承力元参数
1.2 整车动力学模型
以国内某高速列车为例,建立包含车体、构架、轴箱、轮对等部件的整车动力学模型,并将前文所述的驱动系统以子结构形式导入到整车动力学模型中,从而建立含有驱动系统的整车动力学模型。根据其动力学模型参数确定铰接、力元Marker点的坐标参数。模型中各部件在整车系统中的位置通常由铰接来确定,各部件间的连接关系由力元、铰接来确定。轮对与构架之间建立一系悬挂系统,构架和车体之间建立了二系悬挂系统。图2为该动力学模型拓扑图。

图2 动力学模型拓扑图
1.3 刚柔耦合动力学模型
高速列车齿轮箱体一般采用铝合金材料铸造薄壁结构,多边形工况下齿轮箱处于异常振动状态,可能存在疲劳损伤等问题从而影响其疲劳寿命。为研究其所受应力及疲劳寿命,需要将齿轮箱体柔性化处理,并导入到整车模型中建立刚柔耦合动力学模型。首先采用Solid works三维软件绘制箱体几何模型,其次采用Hyprmesh软件进行网格划分,然后在Ansys软件中进行全自由度模态分析,由于模型太大无法直接用于Simpack软件,故还需进行自由度缩减生成子结构文件,并进行模态分析得到模态结果文件;最后导入到Simpack软件,在FEMBS模块中生成柔性体文件,完成刚柔耦合动力学模型的建立,所建模型如图3所示。
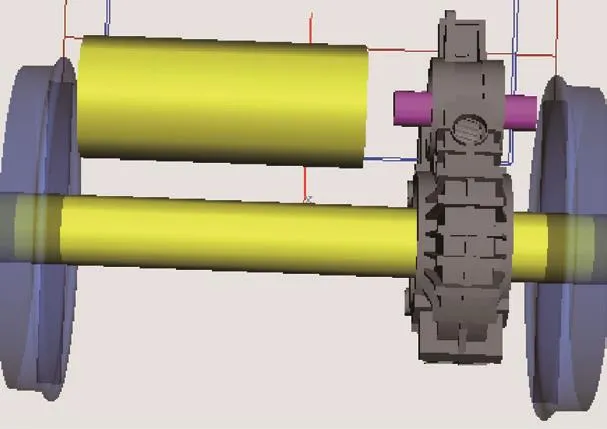
图3 刚柔耦合动力学模型示意图
2 工况确定
2.1 车轮多边形
高速列车运行过程中普遍存在车轮多边形现象。当车轮多边形某一阶占主导时,为车轮周期性不圆顺,此时轮径差出现周期性变化[7]。该现象产生后,会引起强烈的轮轨冲击,此时轮轨激励经轮对向上传递到齿轮箱,使其长期处于异常振动状态,产生疲劳损伤影响疲劳寿命。本文采用简谐波函数法来定义车轮周期性不圆顺。则车轮多边形可以采用公式(1)来仿真模拟[8]。

式中:Δr为轮径差,A为多边形幅值,n为多边形阶数,β为车轮转动角度,β0为初始相位角,r(β)为车轮实际半径随车轮转动角度变化,R为车轮滚动圆半径,ω为车轮转动角速度。
2.2 工况确定
轮轨垂向力反应轮轨间受力情况,而齿轮箱垂向加速度能够有效反应齿轮箱振动情况。本文通过分析高速列车运行速度为350 km/h时,正常工况以及三阶不同幅值的多边形工况下轮轨垂向力、齿轮箱垂向加速度的变化,来确定引起齿轮箱剧烈振动的极端工况。根据文献[9]可知,对于三阶多边形而言,0.1 mm即为实际测量中的最高幅值,故本文将三阶多边形的幅值设置为0.01 mm、0.04 mm、0.07 mm、0.1 mm。
图4所示为350 km/h正常工况以及350 km/h 三阶不同幅值的多边形工况下轮轨垂向力随时间变化情况。可知,正常工况下轮轨垂向力变化稳定且幅值很小,在三阶0.01 mm的多边形工况下轮轨垂向力变化趋势与正常工况下基本一致。随着多边形幅值进一步增大,轮轨垂向力幅值逐渐增加且波动明显。当多边形幅值增大到0.1 mm时,轮轨垂向力变化极不稳定,并伴随多个峰值,其中最大峰值已接近400 kN,明显大于轮轨垂向力的正常限值170 kN。

图4 轮轨垂向力
图5所示为上述不同工况下齿轮箱垂向加速度随时间变化情况。可知,正常工况下齿轮箱垂向加速度变化稳定且幅值很小,在三阶0.01 mm的多边形工况下齿轮箱垂向加速度变化趋势与正常工况下基本一致。随着多边形幅值进一步增大,齿轮箱垂向加速度逐渐增加。当多边形幅值增大到0.1 mm时,齿轮箱垂向加速度大小明显高于其他工况,且变化极不稳定。
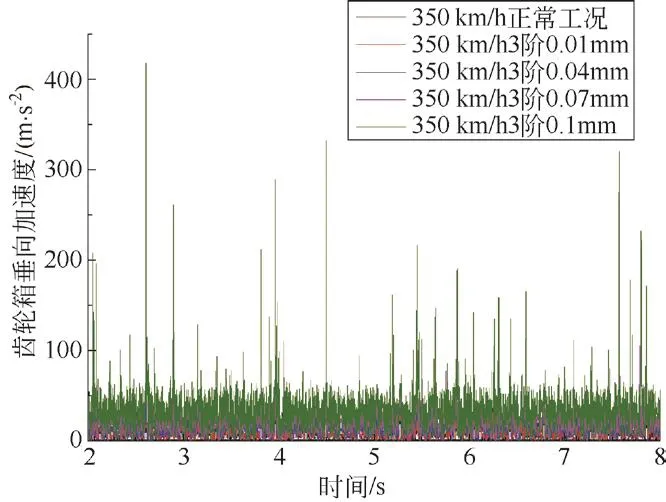
图5 齿轮箱垂向加速度
在上述各工况下对齿轮箱垂向加速度进行统计,得到其有效值和最大值随车轮多边形幅值的变化如图6所示。由图可知,当车轮多边形幅值为0 mm时即正常工况下齿轮箱垂向加速度的有效值和最大值很小,分别为11.67 m/s2、46.29 m/s2。随着车轮多边形幅值的增大,其有效值和最大值均增大。当多边形幅值增大到0.1 mm时,齿轮箱垂向加速度的有效值和最大值分别为42.26 m/s2、417.28 m/s2,远高于其他工况。

图6 齿轮箱垂向加速度有效值和最大值
综上所述,在350 km/h 三阶0.1 mm车轮多边形工况下,轮轨垂向力、齿轮箱垂向加速度均急剧增大,齿轮箱异常振动。该工况为极端工况,此时齿轮箱的疲劳寿命可能会受到影响。因此,本文在后续分析中将350 km/h 三阶0.1mm作为车轮多边形的典型工况(以下简称多边形工况)。
3 齿轮箱应力分析与疲劳寿命分析
3.1 模态叠加法
模态叠加法[10,11]是一种基于模态的正交性和展开定理的求解动力学响应的近似方法,对于高速列车齿轮箱这种多自由度系统而言,可通过对其动力学方程进行解耦,得到齿轮箱在模态坐标响应,然后通过线性变化得到物理坐标响应。多自由度系统的动力学方程一般可表示为

式中:{F(t)}为系统激振力,[M]为质量矩阵,为加速度向量,[C]为阻尼矩阵,{}为速度向量,[K]为刚度矩阵,{x}为位移向量。
通过线性变换{x}=[Φ]{xP}并结合模态矩阵[Φ]正交性可将式(3)转换到模态坐标系下,实现对原动力学方程的解耦,其模态坐标系下的模态方程为
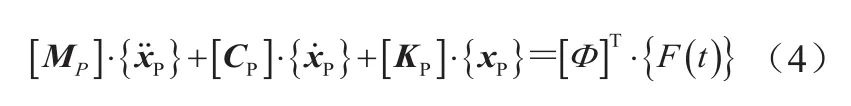
式中:[MP]为模态质量,[MP]=[Φ]T· [M] · [Φ];[KP]为模态刚度,[KP]=[Φ]T· [K] · [Φ];[CP]为模态阻尼,[CP]=[Φ]T· [M] · [Φ] ;{xP}为模态坐标系下的位移向量。
对式(4)进行求解,得到各阶模态位移响应即各阶模态的主坐标,左乘各阶模态对应的主阵型,然后将各阶模态线性叠加最终得到物理坐标系下的响应。
基于齿轮箱有限元模型模态对应的固有频率、特征值所对应的特征向量以及动力学分析获得的模态位移,采用模态应力恢复法得到该模型各节点的应力时程,模态应力为

式中:Eσ为模态应力矩阵,其各元素的值与材料弹性模量、泊松比有关;为模态位移矢量即各阶模态位移的矢量表达式。
3.2 应力分析
应力分析是疲劳寿命分析的基础,为分析高速列车车轮多边形对齿轮箱疲劳寿命的影响,首先需要分析计算该工况下齿轮箱的应力。本文将仿真分析得到的齿轮箱的力和边界条件以时间历程载荷谱的形式输入到基于模态叠加法的瞬态响应分析中,得到模态位移响应,并通过模态应力恢复法得到齿轮箱各节点的应力时程[11]。
对齿轮箱进行应力分析,通过观察多边形工况下齿轮箱应力云图(见图7)可知,齿轮箱多处出现应力集中,即存在多个危险点。主要包括输出轴轴承端支撑筋处A点;输入输出轴轴承连接板处B点;齿轮箱下箱体处C点;齿轮箱上箱体处D点;输入轴轴承端散热筋处E点;齿轮箱上箱体观察孔处F点。图8为上述6点在多边形工况以及正常工况下的应力时程,表1为两种工况下6点的von-mises应力最大值。

图7 齿轮箱应力云图

由图6和表1可知,与正常工况相比,多边形工况下齿轮箱各点的应力波动剧烈且最大值明显增大。在多边形工况下,上述6点中输出轴轴承端支撑筋处A点的应力最大。

表1 齿轮箱应力最大值 MPa
3.3 疲劳寿命分析
采用雨流计数法将齿轮箱各节点的应力时程转换成等效的循环载荷谱(为非对称应力循环载荷),通过古德曼应力修正将其转换成可适用于材料S-N曲线的对称应力循环载荷,基于Miner线性疲劳累积损伤理论对齿轮箱进行疲劳寿命分析。
材料的S-N曲线是疲劳寿命分析的基础,通常利用疲劳试验机对材料的标准式样进行疲劳试验,得到试件的疲劳应力与循环次数。用N为循环次数,S为应力,可得到材料的S-N曲线。S-N曲线通常采用幂函数式表示,即

式中:m、C为材料的常数。
根据线性Miner法则,若在应力Si作用下材料达到破坏的总循环次数为Ni,则材料在应力Si作用下循环ni次的疲劳损伤为ni/Ni。将各级应力水平下疲劳损伤线性叠加得到材料的疲劳累积损伤D,通常认为当其达到临界值1时产生破坏[12],表达式为

式中:ni、Ni分别为应力Si作用下的循环次数和疲劳寿命。
采用参考文献[13]的标准对铝合金材料铸造结构的齿轮箱进行评估,当m=7循环次数为108时,应力为22.9 MPa,超过该循环次数则不产生损伤。在Miner法则下,前述齿轮箱上6点所能达到的总循环次数如表2所示。循环次数乘以该载荷时间历程下列车所行使的距离即为该点的服役里程,则6点所能达到的服役里程如表3所示。由表3可知,多边形工况会对齿轮箱输出轴轴承端支撑筋处A点造成较大的疲劳损伤,其所能满足的服役里程仅为256万km,小于正常使用寿命1 200万km。因此,在高速列车实际运营中,应高度重视车轮多边形对齿轮箱疲劳寿命带来的影响,可通过适当的车轮镟修来降低车轮多边形对齿轮箱疲劳寿命的影响。
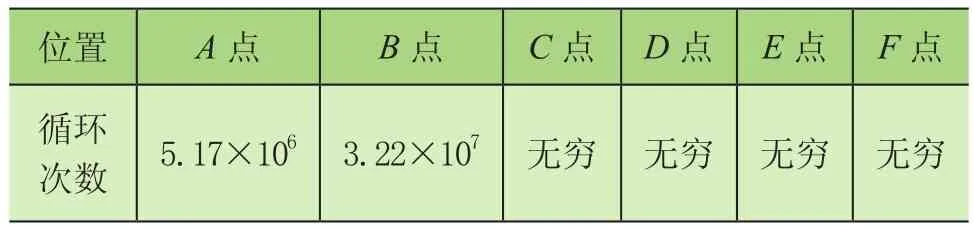
表2 齿轮箱不同位置所能满足的循环次数

表3 齿轮箱不同位置所能满足的运行里程 万km
4 结语
1)建立了包含齿轮箱支撑轴承的驱动系统和齿轮箱有限元模型的刚柔耦合整车动力学模型,利用Simpack软件中的88号轴承力元建立齿轮箱支承轴承,将齿轮箱与输入、输出轴相连,更好地反映齿轮箱的振动情况。
2)通过分析不同多边形幅值下轮轨垂向力以及齿轮箱垂向加速度的变化,发现350 km/h 三阶0.1 mm的极端工况下,轮轨垂向力及齿轮箱垂向加速度较其他工况显著增大,齿轮箱振动剧烈。
3)在350 km/h 三阶0.1mm多边形工况下,齿轮箱多处出现应力集中,存在多个危险点;其中齿轮箱圆锥轴承安装座支撑筋处应力最大,其疲劳寿命只能达到256万km,远小于1 200万km的正常寿命。
