湍流特性对矩形高层建筑风荷载影响的研究

刘 奕，陈水福

(浙江大学 建筑工程学院，杭州 31005)

0 引 言

风荷载是高层建筑的主要控制荷载，而风的湍流特性是影响风荷载分布特性尤其是脉动与极值特性的重要因素。探讨来流湍流特性对建筑风荷载的影响一直是学术界和工程界十分关注的课题。

湍流度和湍流积分尺度是表征风的湍流特性的两个主要参数，现有研究也主要从这两个方面出发研究其对建筑风荷载及周围绕流特性的影响。文献[1-3]研究了湍流特性对二维矩形棱柱绕流的影响，其中Lee[1]发现湍流度增大使侧风面风压恢复提前、背风面负压（均指绝对值）减小；Laneville[2]发现湍流度增大使平均剪切层曲率半径减小，从而使阻力系数最大值对应的深宽比减小；Nakamura和Ohya[3]发现湍流强度和湍流积分尺度均对背风面负压有较大影响。文献[4-9]研究了湍流特性对二维平板钝体周围分离再附流的影响，其中Hillier和Cherry[4]发现湍流度对平均风压和脉动风压均有很大影响，而湍流积分尺度对平均风压影响不大，对脉动风压影响很大；Nakamura和Ozono[5]发现分离泡内平均风压分布在湍流积分尺度比（即湍流积分尺度与模型特征尺寸之比）小于2时变化不大，而超过2时逐渐趋近均匀流下的分布；Li和Melbourne[8-9]发现平均风压在尺度比大于3.6时受湍流积分尺度影响明显，脉动风压和极值负压随湍流度和湍流积分尺度增大而增大，湍流积分尺度对极值负压的影响程度随湍流度增大而提高。顾明和叶丰[10-11]研究了不同风场下不同体型高层建筑的气动力幅值和频域特性，发现随地面粗糙度增加，脉动升力、阻力系数增大，升力系数谱频带变宽、能量减小；苏万林[12]研究了湍流对高层建筑表面风压的影响，发现在湍流强度很大时，背风面和侧风面可能出现小正压；Akon和Kopp[13]通过粒子图像测速试验，研究了湍流度和湍流积分尺度对低矮房屋屋顶分离再附流的影响，发现湍流强度增大会使流动更早再附，且影响风压恢复速率，而湍流积分尺度对再附长度影响不大。总体而言，目前国内外湍流特性研究主要针对深宽比较小的矩形截面钝体或建筑，或是深宽比无限大的二维平板，但对于介于二者之间的有限深宽比的钝体研究较少。但是，这类钝体随着深宽比的变化，其表面风压是否会因流动分离再附的改变而表现得显著不同，其中来流湍流特性的影响程度如何，目前并不明确。

鉴于此，本文以国内广泛存在的具有较大深宽比范围的板式住宅高层建筑为背景，对4种不同地貌条件下9种深宽比的矩形截面高层建筑进行了风洞测压试验，分析了湍流度与湍流积分尺度对不同深宽比建筑平均、脉动与极值风压，以及横风向气动力谱和周围绕流特性的影响规律。

1 风洞试验

1.1 风场模拟

本次试验在加拿大西安大略大学（University of Western Ontario，UWO）边界层风洞Ⅱ的高速试验段中进行。该试验段长30.0 m，宽3.4 m，高2.1 m，最大风速可达40 m/s。试验段前端拥有全自动的粗糙元控制系统，配合入口处可选放置的格栅、尖劈和挡板等湍流产生装置，可以精确模拟各种地貌下的大气边界层。

本次试验共模拟了4种地貌，其中O1、O2地貌与S1、S2地貌使用了两种不同的粗糙元配置，分别模拟开阔地貌（Open terrain）与郊区地貌（Suburban terrain）风场；O1、S1地貌较O2、S2地貌在风洞入口处多使用了一块0.38 m高的挡板。根据Holmes和Osonphasop[14]，挡板的存在可以产生更大尺度的湍流，实现对湍流强度和湍流积分尺度的同步控制。试验风速采用Cobra Probe进行测量，采样频率为1 250 Hz，采样时间30 s。来流风场缩尺比为1∶200。平均风速剖面与湍流度剖面根据工程科学数据库（ESDU）[15-16]建议的对数率进行模拟，试验值与理论值吻合良好。表1列出了各地貌的地表粗糙长度z0（对应对数率剖面）与粗糙度指数α（对应指数率剖面）。图1给出了4种地貌风剖面的比较，图中H为建筑顶部高度，和Iuz分别为高度z处的平均风速和湍流强度。由图可见，由于粗糙元配置的不同，O类地貌与S类地貌的风剖面差异较大；由于挡板的存在，S1地貌较S2地貌的湍流强度有小幅提高，但O1地貌与O2地貌下的湍流度相差不大。

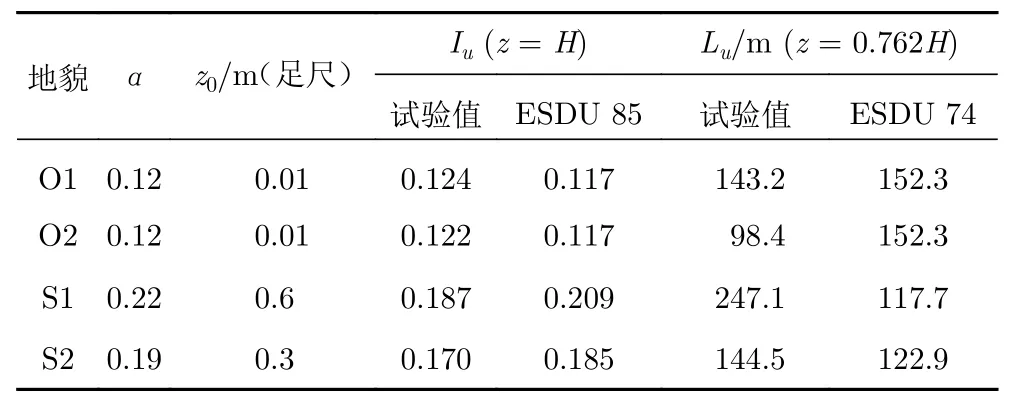
表1 各地貌下的风场参数Table 1 Parameters for the upstream flow under different terrains

图1 平均风速剖面与湍流度剖面Fig. 1 Mean wind velocity and turbulence intensity profiles

来流风场的湍流积分尺度按ESDU 74[17]建议的经验式进行模拟。湍流积分尺度试验值按下式计算：

式中，Lu为湍流积分长度，Lt为湍流积分时间尺度，ρuu(τ)为脉动风速自相关系数，τ为时差，τ0为自相关系数收敛至0时对应的时差。各地貌下z= 0.762H（靠近驻点）高度处的湍流积分长度试验值及ESDU 74结果可见表1，其中O1地貌下试验值与ESDU值较为接近。O1、S1地貌分别较O2、S2地貌具有更大的湍流积分长度，可见挡板的存在能使湍流积分长度显著增大，增幅在50% ～ 100%左右。

脉动风速谱按ESDU 74[17]建议的Von Karman谱进行模拟。图2给出了试验值与理论值的拟合情况，图中f为频率，Suu为脉动风速功率谱密度，由图可见二者吻合良好。图3给出了4种地貌风速谱的比较，图中曲线在竖向的相对位置代表湍流度的相对大小，在水平向的相对位置代表湍流积分尺度的相对大小。由图可见，由于S类地貌的湍流度总体大于O类地貌，故S类地貌曲线整体在O类地貌上方；由于1类地貌湍流积分尺度总体大于2类地貌，1类地貌曲线整体较2类地貌略微偏左。

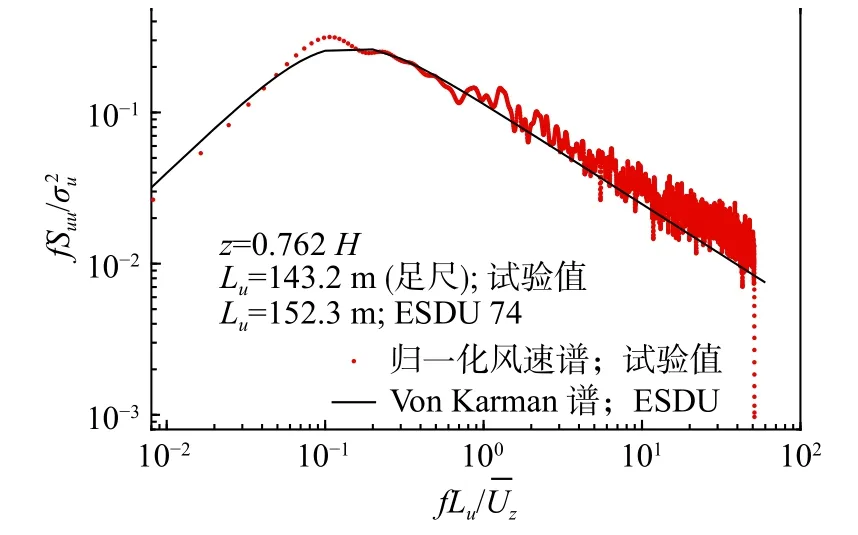
图2 O1地貌下脉动风速谱Fig. 2 Wind velocity spectrum under O1 terrain

图3 各地貌脉动风速谱Fig. 3 Wind velocity spectra under different terrains

1.2 模型及试验参数

本次模型为一矩形截面高层建筑刚性模型，缩尺比为1∶200。模型共由11段组成，如图4所示，其中段1～段6的深宽比为0.5（按图中风向），段7～段11的深宽比为1，通过拼接组合及调整摆放角度可获得深宽比为0.125～8的模型工况。沿模型高度方向共布置了7个测点层，各层高度分别为0.1H、0.3H、0.5H、0.65H、0.8H、0.9H、0.98H，各层布置方式相同。深宽比为8的工况的模型参数如表2给出，平面测点布置如图4所示。测压孔通过测压管道系统接入至扫描阀上，扫描阀最终通过2048通道全自动测压扫描系统被接入至PC机上，关于测压管道与扫描系统的详细信息可参见文献[18]。本次试验对深宽比为1/8、1/5、1/3、1/2、1、2、3、5、8的共计9种深宽比工况进行了4种不同地貌下的同步风压测试，风洞试验照片如图5所示。试验风压采样频率为400 Hz，采样时长为90 s，相当于足尺1H以上。风洞内边界层高度以上的参考风速为14.0 m/s。对于每个深宽比工况，进行了不同风向的测试，本文仅针对正交风向情况进行研究。

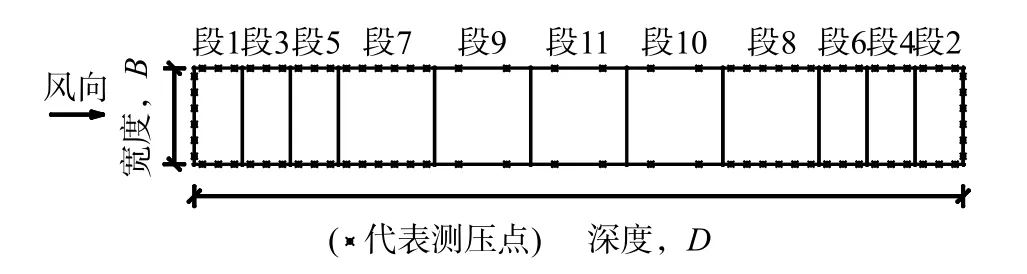
图4 模型平面测压点布置Fig. 4 Plan layout of pressure taps on the testing model

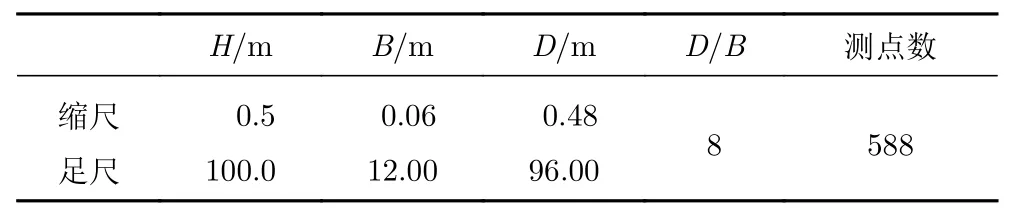
表2 D /B = 8工况模型参数Table 2 Model parameters for the configuration of D /B = 8

图5 模型及风洞试验照片Fig. 5 Photos of the models in the wind tunnel

1.3 数据处理

风压系数按风工程界惯例，采用建筑顶部高度H作为归一化高度，定义如下：

式中，pi为测点i的风压值，p∞为静压值，ρ为空气密度。

为考察建筑某一表面的整体风压系数CpA或风荷载合力系数CF的大小，将其定义如下：

式中：Cpi为测点i的风压系数，Ai为测点i的控制面积，A为进行计算的建筑表面的面积。由上式可见，整体风压系数即为测压点风压系数在整个表面上的面积加权平均值。

极值分析方法对极值估计结果有很大影响。本文采用Gumbel拟合法进行极值估计，其中Gumbel分布参数应用Lieblein BLUE法确定，由文献[19]可知，该方法具有较高的准确性与稳定性。关于该方法的细节可参见文献[20-22]。

2 平均风荷载

2.1 迎风面

图6给出了各地貌下建筑迎风面整体风压系数的平均值随深宽比的变化情况。为降低不同地貌风速剖面的差别产生的影响，该值由以测压点高度作为归一化高度的局部风压系数计算获得，以CpLA表示。由图可见，各深宽比工况迎风面上的整体风压系数差别较小，这是由于对于除边缘附近的迎风面区域，气动力受建筑本身引起的非定常流的作用很小，基本仅受来流的湍流特性影响。1类地貌下整体风压系数的平均值较2类地貌要大，可见迎风面上平均风压系数与湍流积分尺度呈正相关。湍流度对迎风面上平均风压系数的影响规律不明确。

图6 迎风面整体风压系数平均值随深宽比的变化情况Fig. 6 Variation of the mean area-averaged pressure coefficients with the depth-to-width ratio on the windward surface

2.2 侧风面

Ruderich和Fernholz[23]通过对二维钝体分离再附流下的平均风压分布的研究，发现在均匀来流下，无论钝体体型及雷诺数是否改变，在距钝体前缘的流向距离d被平均再附长度Xr归一化时，分离再附流下的约化风压系数沿 流向的分布具有相同的分布曲线。其中约化风压系数如下式定义：

上述研究基于的流场为均匀来流，即低湍流度来流。Akon和Kopp[14]基于低矮建筑顶部绕流的粒子图像测速（PIV）试验数据及现有文献中针对二维矩形棱柱侧边绕流结果，给出了平均再附点处值 随湍流度变化的线性拟合公式：

通过上式即可根据来流某高度处的的湍流度获得平均再附点处的约化风压系数值 ，再结合风洞试验数据并根据式(4)获得平均再附点处的平均风压系数值，进而获得平均再附长度。尽管钝体体型可能对周围绕流产生一定影响，但鉴于分离再附流及其下风压分布特性的相似性，本文在估算高层建筑侧边绕流的平均再附长度时采用文献[14]给出的方法是合理的。

图7给出了D/B= 5、2、1的建筑在各地貌下侧风面上的平均风压系数分布，这三个工况分别对应再附、部分再附与近乎完全分离3种不同的绕流特性，由图可以非常直观地看到地貌对侧风面风压分布的影响。为了更准确地进行考察，图8同时给出了平均和脉动风压系数沿水平方向的分布曲线。此外，表3对平均流动再附的情况给出了按Akon和Kopp[14]方法估算的平均再附长度。

图7 侧风面平均风压系数分布Fig. 7 Mean pressure coefficient distributions on the side surface

图8 侧风面z/H = 0.65处平均与脉动风压系数分布Fig. 8 Mean and fluctuating pressure coefficient distributions at z/H = 0.65 on the side surface

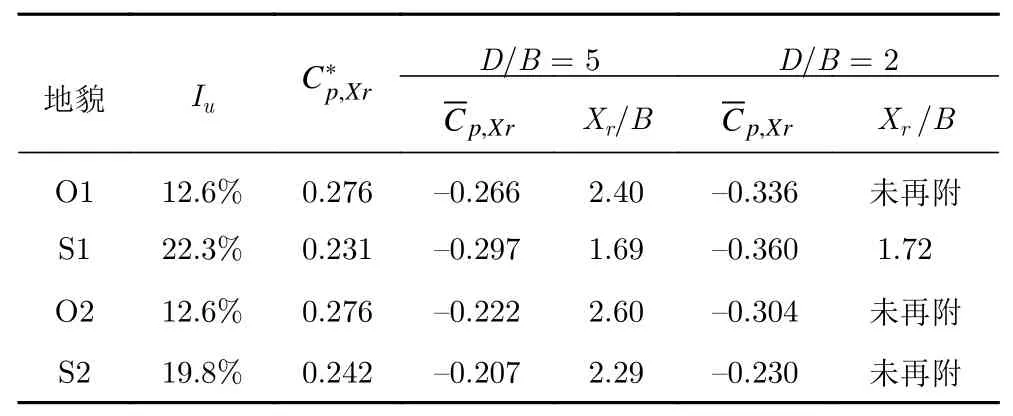
表3 侧风面z/H = 0.65处平均再附长度Table 3 Mean reattachment lengths at z/H = 0.65 on the side surface

对于D/B= 5和D/B= 2的建筑，即平均流动再附和部分再附（O1地貌下）的情况，S类地貌较O类地貌下分离泡内负压更小（均指绝对值），风压恢复更为提前。由表3可见，对D/B= 5的情况建筑，S1地貌下平均再附点出现位置较O1地貌下提前约30%。对于D/B= 2的建筑，随着湍流度的增大，平均流动状态已从O1地貌下的未再附，转变为S1地貌下的再附。值得注意的是，在平均再附点处，风压尚未完全恢复。这些规律与诸多针对二维平板钝体的研究（如文献[4]）结果相似，但本文明确给出了三维棱柱尤其是侧边绕流部分再附情况的风压分布。对于D/B= 1的建筑，即平均流动近乎完全分离的情况，与上述两种情况相似，S类地貌下分离流下负压更小；O类地貌下整个侧风面上均呈现较大负压，而S类地貌下在靠近尾缘处已经开始出现风压恢复的趋势。由以上可见，湍流度增大使分离流下平均负压减小、风压恢复提前、平均再附长度减小。另外，对于深宽比介于1到2的情况，即平均流动近乎完全分离及部分再附的情况，湍流度对平均风压分布影响较大。

对于脉动风压系数，由图8可见，对于D/B= 5和D/B= 2的建筑，在分离泡内，S类地貌下的脉动风压系数较O类地貌明显要大，且曲线峰值出现位置较O类地貌明显靠前。许多针对均匀流下二维棱柱周围绕流的研究表明，最大脉动风压出现于Kelvin-Helmholtz涡卷起、配对并分解成湍流之后，一般该位置刚好出现在平均再附点前[4,24]。而由图8可见，O1地貌下最大脉动风压出现在0.59Xr处，显著提前于平均再附点，S1地貌下则更为提前，出现在0.44Xr处，该规律与文献[4，24]发现相似。此外，在风压恢复过程中，对于平均流动再附情况，S类地貌的平均风压系数仍较O类地貌偏小，但二者之间的差距明显减小，两类地貌下脉动风压系数的差距也明显减小，分布曲线几乎趋于一致。对于平均流动部分再附情况，两类地貌下脉动风压系数在建筑尾缘处均略微增大，O类地貌增幅较S类地貌略微偏大。对于D/B= 1的建筑，流动近乎完全分离，即整个侧风面均处于分离泡下，故S类地貌下整个侧风面上的脉动风压系数均较O类地貌要大。由以上可见，湍流度增大会使分离再附流下脉动风压增大，脉动风压峰值出现位置更靠近前缘。

相较湍流度的影响，湍流积分尺度对平均风压分布的影响较小，但仍对平均绕流有一定的效应。总体上2类地貌较1类地貌平均负压略微偏小。在靠近前缘处，约0.33Xr（O1地貌）内，2类地貌则明显较1类地貌要小。对于平均流动再附或部分再附的情况，在风压恢复过程中，二者之间差距明显减小；对于流动近乎完全分离的情况，在整个侧风面上，1类地貌下的平均负压均较2类地貌要大。对于D/B= 5情况风压恢复过程及恢复后的平均风压系数，S2地貌较S1地貌偏大可能是由于S2地貌下的湍流度较小导致的。由以上分析可知，湍流积分尺度减小使总体平均负压减小、靠近前缘区域平均负压明显减小。

同时，由图8可见，O2、S2地貌下的脉动风压分布曲线形状分别与O1、S1地貌相似，但前者脉动风压系数值总体上均分别小于后者，说明湍流积分尺度减小会使总体脉动风压减小，但对脉动风压分布曲线形状影响不大。

由图3可见，在湍流度相同的情况下，湍流积分尺度较小的风场的脉动风速谱，通常在高频区具有更多的能量分布，即含有较少的大尺度湍流成分、而含有更多的小尺度湍流成分。这些分析表明，大尺度湍流使分离流下平均风压和脉动风压值增大，而小尺度湍流促使分离流更早再附，且使分离流下的平均风压和脉动风压值减小、峰值出现位置更靠近前缘。

需要说明的是，上述分析大多基于侧风面z/H=0.65高度处，在该高度处建筑侧风面绕流状态较为接近二维钝体。而由图7可见，建筑侧风面风压分布沿高度方向变化明显，呈现明显的三维效应。各地貌下侧风面最大平均负压均出现在建筑前缘顶角处。

2.3 背风面

背风面上平均风压分布较为非常均匀，故本节仅给出了各地貌下背风面整体风压系数随深宽比的变化情况，如图9所示。由图可见，背风面上的整体风压基本均在深宽比为0.5至1时达到最不利。S类地貌下背风面上的平均风压系数均小于O类地貌，对于平均流动再附的情况及在深宽比非常小时，两类地貌下的差距较小。但对于流动近乎完全分离及部分再附的情况该规律非常明显，该深宽比范围内的建筑的湍流度效应较大。1类与2类地貌下的平均风压系数差距较小，通常1类地貌略微大于2类地貌。由此可见，背风面上的负压大小与湍流度通常呈负相关，而与湍流积分尺度呈正相关。

图9 背风面整体风压系数平均值随深宽比的变化情况Fig. 9 Variation of the mean area-averaged pressure coefficients with the depth-to-width ratio on the leeward surface

3 极值风荷载

3.1 迎风面

迎风面上，各深宽比建筑迎风面上的极值风压分布非常相似，故图10仅给出D/B= 1工况迎风面竖直中心线处极大值风压系数分布。由图可见，1类地貌、S类地貌极值风压系数分别较2类地貌、O类地貌要大。可见，迎风面上的极值正风压系数是由湍流度和湍流积分尺度综合决定的，其中极值风压系数与湍流积分尺度明显呈正相关关系。

图10 D/B = 1工况迎风面竖直中心线处极大值风压系数分布Fig. 10 Maximum pressure coefficient distributions along the windward vertical centerline for D/B = 1

3.2 背风面

背风面上的极值风压分布较为均匀，湍流特性对极值风压的影响规律也较为简单。由图11给出的竖直中心线上的极小值风压系数分布曲线容易看到，1类地貌下的极值负压普遍较2类地貌要大；但S类地貌与O类地貌下的差别未呈现明显的规律。这可能是由于S类地貌来流湍流脉动较大、但因分离流更早在侧边再附而使尾流有所减弱这两种因素相互作用导致的。

图11 背风面竖直中心线上的极小值风压系数分布Fig. 11 Minimum pressure coefficient distributions along the leeward vertical centerline

3.3 侧风面

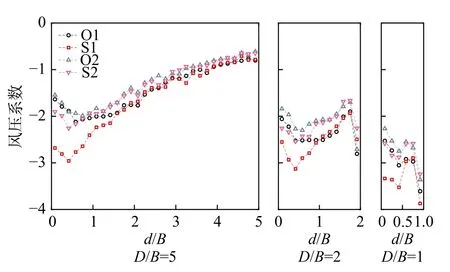
图12 侧风面z/H = 0.65处极小值风压系数分布Fig. 12 Minimum pressure coefficient distributions at z/H = 0.65 on the side surface

图12给出了侧风面z/H= 0.65处的极小值风压系数分布曲线。由图可见，对于D/B= 5和D/B= 2的建筑，S1类地貌分离泡内的极值负压较O类地貌明显要大，尤其是在靠近前缘位置处，这与湍流度对平均风压分布的影响规律相反。但相似的是，S类地貌下最大极值负压出现的位置较O类地貌更为提前，但最大极值负压一般均出现在0.2Xr～0.3Xr处，这与文献[6]的结果基本相符。对于平均流动完全再附的情况，极值负压在达到最大值后一般随到前缘距离的增大而减小；但对于平均流动部分再附或近乎完全分离情况，极值负压则在尾缘突然显著增大，不同地貌对尾缘处较大负压值的影响规律不明显。由此可见，湍流度与分离再附流下的极值负压呈正相关关系。

湍流积分尺度对侧风面极值风压分布也有一定影响。由图12可见，1类地貌下极值风压系数总体上较2类地貌下要大，说明湍流积分尺度减小会使总体极值负压减小。对于湍流积分尺度对分离再附流下的最大极值负压的影响，考虑到湍流积分尺度较大的风场通常在低频区具有更多的能量分布，即含有较多的大尺度湍流成分，可以发现更大尺度的湍流可能是产生更大的极值负压峰值的原因。故本文也部分验证了文献[6]中提到的“最大极值负压由分离剪切流在钝体表面附近卷起而形成的较大旋涡引起”。

图13 横风向气动力谱Fig. 13 Cross-wind aerodynamic force spectra

4 横风向气动力谱

图13给出了深宽比D/B= 0.33、1、2和5的建筑在4种地貌下的横风向气动力谱的比较。对于D/B=1工况，尽管S类地貌来流脉动风速谱较O类地貌要高，但对于气动力谱，O类地貌下谱峰所含能量较S类地貌要大，这可能是由于S类地貌湍流度更大、分离流已开始部分再附于建筑侧面导致的。相比之下，D/B= 0.33工况的建筑尾体较短，气流在各地貌下均完全分离并脱落于尾流中，S类地貌下气动力谱则整体高于O类地貌。对于D/B= 2工况，各地貌下分离流均开始再附，横风向气动力谱则呈现更宽的谱峰。对于D/B= 5工况，各地貌下分离流均近乎完全再附，谱在高频区的峰消失。总体而言，湍流度对深宽比介于1到2的建筑、即流动近乎完全分离及部分再附的情况影响较大。

图14给出了4种地貌下建筑斯托罗哈数St随深宽比的变化曲线及与文献结果的比较。文献[25]数据较本文数据明显要小，且其给出了深宽比直至4的斯托罗哈数结果，而本文对于深宽比大于2的工况（S类地貌下则对于深宽比大于1的工况）的斯托罗哈数因谱峰过宽已很难由谱峰位置确定出来。但是对于深宽比为1的工况，本文数据与文献[26]非常接近。由图14可见，整体上各地貌下的St相差不大。

图14 斯托罗哈数St随深宽比变化情况Fig. 14 Strouhal number variation with the depth-to-width ratio

5 结 论

本文对4种不同风场下9种深宽比的矩形截面高层建筑各立面的平均、脉动、极值风压与横风向气动力谱进行了考察，获得了如下结论：

1）随湍流度增大，分离流更早再附于侧风面上，其中郊区地貌下较开阔地貌再附提前约30%。湍流度增大使分离流下平均负压（均指绝对值）减小、极值负压增大，最不利脉动风压与极值负压出现位置较再附点更为提前。随湍流度增大，背风面上平均负压减小，但极值负压变化不明显。对于方形建筑，旋涡脱落频率处的横风向气动力谱能量随湍流度增大有所降低。

2）随湍流积分尺度减小，迎风面上、背风面的平均风压与极值风压绝对值均减小，侧风面分离流下平均负压、脉动风压与极值负压均减小。湍流积分尺度对分离再附流形态及分离流下的风压分布形状影响不大。

3）不同深宽比建筑分离再附流下的平均、脉动与极值风压分布形状相似，但背风面平均风压值以及横风向气动力谱形状差别较大。总体而言，湍流特性对深宽比介于1到2的建筑，也即流动近乎完全分离及部分再附的情况影响较大。

4）大尺度湍流使分离流下平均风压和脉动风压值增大，而小尺度湍流促使分离流更早再附，且使分离流下的平均风压和脉动风压值减小，峰值出现位置更靠近前缘。更大尺度的湍流可能是产生更大极值负压峰值的原因。