基于实行垃圾分类后的垃圾处理与清运方案研究

党亚峥，钟素婷，任倩梅

（上海理工大学 管理学院，上海 200093）

0 引 言

2019年1月31日，上海市第十五届人大二次会议表决通过了《上海市生活垃圾管理条例》，根据规定，居民需将生活垃圾按照可回收垃圾、有害垃圾、湿垃圾、干垃圾4类标准进行分类［1］。垃圾分类需要因地、因时、因人提出分类方法、分类目标、分类重点和实施策略［2］。为了最大限度节省垃圾分类成本，研究人员根据不同状况建立了不同模型。在传统的评估垃圾分类项目的可行性模型中，Saaty等人［3］提出了层次分析法来评估废物处理方案的可行性；Karagiannidis等人［4］设置了有关环境政策、环境影响、经济效益等方面的24个指标，对希腊大雅典地区的5种生活垃圾综合处理方案进行评估。然而这种建立多指标的模型，计算过程比较繁琐，且在此决策过程中目标权重的确定带有一定的主观性。关于垃圾分类再处理的成本分析：前端垃圾分类服务成本指在垃圾分类宣传、督导等所花费的资金，这是必要的成本，很难降低。终端垃圾处理包括垃圾焚烧和湿垃圾处理，该处理成本主要依据当下设备的效率与机能来定，需要机器设备的不断优化更新，不是一个短期能解决的问题。因此，目前主要是通过降低中端垃圾收运成本来降低总成本，即降低垃圾的运输成本。此外，还可以利用废弃垃圾增加相关收入。比如，建立再生资源集散场，将可回收垃圾进行回收处理后再出售。冯思静等人［5］基于此理念建立了效益模型。本文便着力于减少运输成本，建立相关模型。

1 相关建模理论与研究

运输问题主要包括产销平衡、产大于销、销大于产3种情况，其都需要平衡运输问题，即生产数量等于销售数量的运输问题［6］，要寻找其最优运输方案可直接使用表运算法［7］。

产销平衡运输问题建模：设将某种物资从m个产地运输到n个销售地，产地分别编号为D1，D2，…，Dm，销售地分别编号为Q1，Q2，…，Qm，其中产量分别为A1，A2，…，Am，销量分别为B1，B2，…，Bm，从第i个产地到第j个销售地的单位运费为cij，（i=1，2，…m；j=1，2，…，n），从第i个产地到第j个销售地的距离为xij，如式（1）：

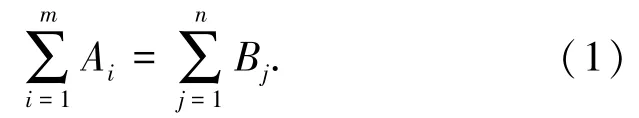
在满足式（1）的条件下，便要规划路线使运输成本最小。根据已知条件建立以下线性规划模型：

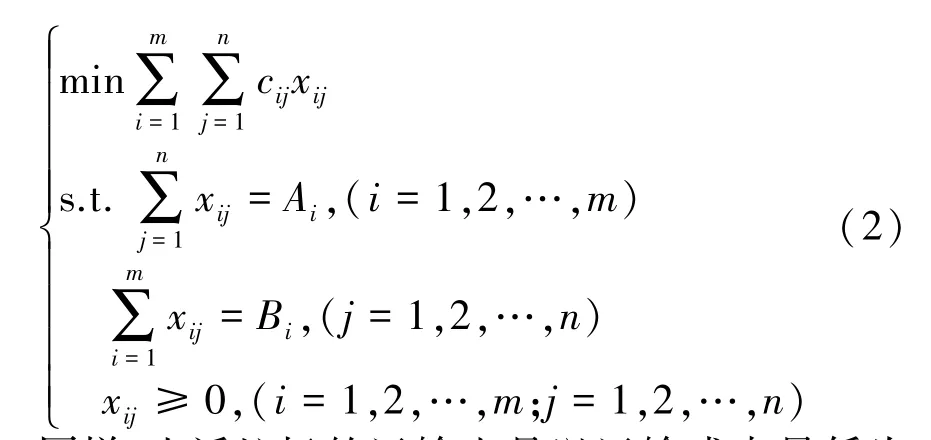
同样，生活垃圾的运输也是以运输成本最低为目标建立线性规划模型来求解［8］。此问题应根据各中转站、街道小区的垃圾处理能力与产生量，以及各转运站到街道小区间的距离确定转运路线。

2 选址问题和运输问题建模及求解

为便于对垃圾分类问题进行建模，给出如下假设条件：

（1）每个转运站的日垃圾量是恒定的；

（2）每个转运站、社区垃圾收集站和垃圾桶内的垃圾必须在同一天清理干净；

（3）不考虑因塞车和运输车辆在行驶过程中发生故障而造成的延误；

（4）运输车没有超载现象；

（5）每个垃圾收集站都位于街道旁边，以确保运输车辆的畅通；

（6）选址问题中每个中转站分别负责一个街道的小区，小区所有聚集点的垃圾都运往此中转站；运输问题中改变各街道垃圾的运输方向，不再是定向运输到某一中转站，而是任意中转站；

（7）每天（早晨或晚上）仅从社区收集一次垃圾；

（8）假设所有运输车辆离开垃圾转运站，最后返回垃圾转运站都以直线路径来计算距离。

2.1 选址问题模型的建立及求解

再生资源集散场的再建，其实就是一个单设施选址问题［9］，需考虑实际地理情况和现有设备。

由杨浦区区政府官方公布数据中查阅可知，2019年杨浦区生活垃圾日均量为800吨，人口总数量约为131万人。因此可以求得人均垃圾产生量为800*1000／（131*10000）=0.611（千克／每天／每人）。根据各街道人口数量，可以粗略计算出各中转站日均垃圾收集量，然后运用Google地球搜索中转站的坐标得到表1。表1中人口数量来自2010年第六次人口普查结果。

表1 垃圾中转站情况表Tab.1 Garbage transfer station situation Table

对于该单设施选址问题，可运用运筹学中的重心法［10］。为使设计的地里位置更优化，可以运用迭代重心法公式。设重心为（x0，y0），则根据公式得到式（3）-式（6）：

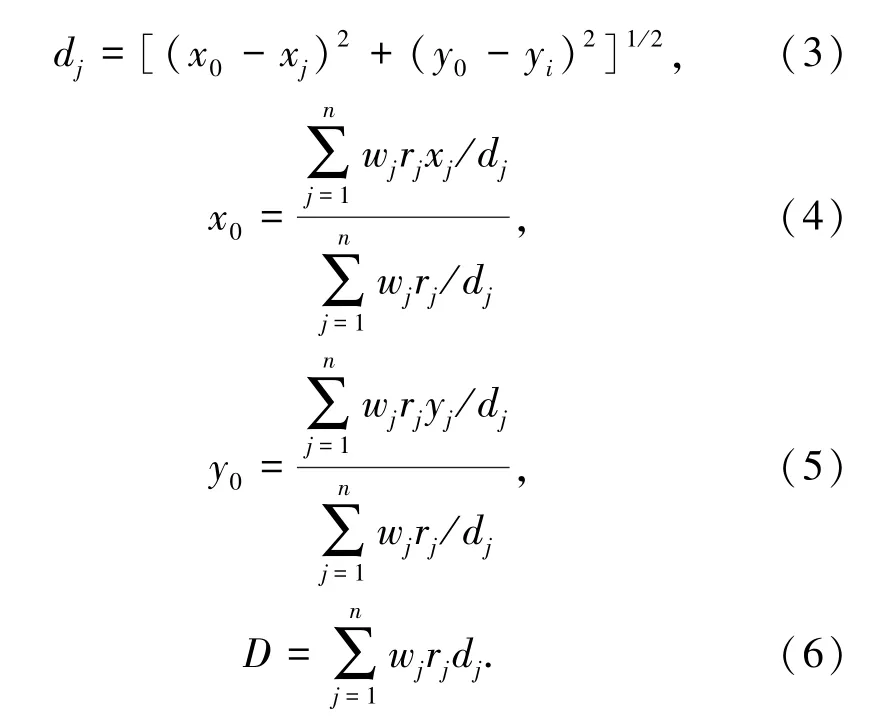
式中，xi为第i个地点的x坐标；yi为第i个地点的y坐标；wi为第i个地点的货物量；ci为第i个地点的运输费。

由于运输费主要取决于运输距离，各中转站距离街道小区较近，人工成本所差无几，汽油费也相同，所以运输率相同。故用MATLAB可以快捷方便地得到再生资源集散场的经纬坐标为（121.530，31.302）。

2.2 运输问题模型的建立及求解

在垃圾车清运路线设计上，除考虑运输路线最短外，还应考虑各中转站的垃圾处理能力。如果垃圾中转站当日不能处理完垃圾，则需要将垃圾存储到第二天来处理，这样便会产生垃圾存储成本，而建立的目标函数是使得成本最少［11］。通过查阅资料可得各中转站的日均垃圾处理量，再计算出各街道小区到中转站之间的距离，最后根据产销平衡理论进行求解。各中转站情况见表2。

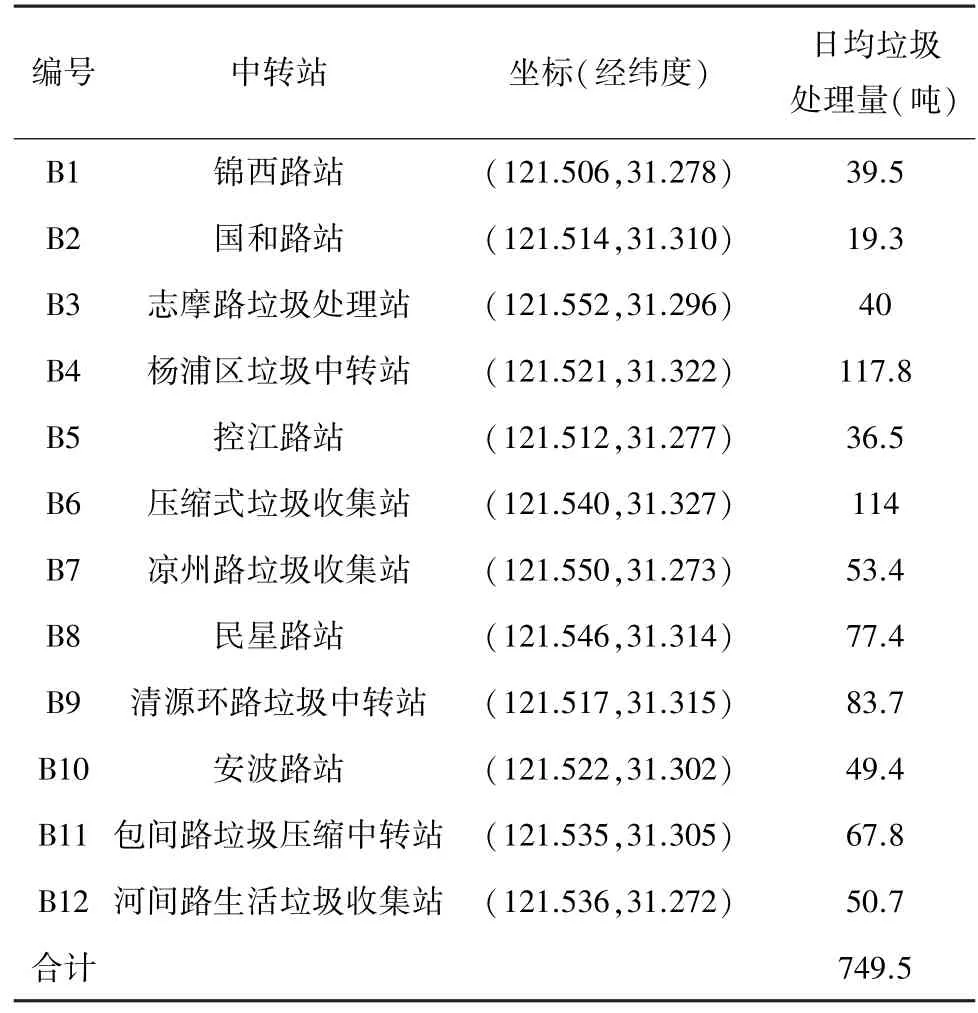
表2 各中转站情况Tab.2 Situation of each transfer station

由于街道小区垃圾箱房、垃圾聚集点数量较多，暂且以各街道涵盖的面积经纬度坐标分别求和再平均得到的中心表示垃圾聚集点。得到各街道情况，再根据经纬度坐标之差，可以求得各地点之间的直线距离。由表1、表2可知，12个街道垃圾产生量总和为802.854吨，而12个垃圾中转站的垃圾处理能力却只有749.5吨，相当于运输问题中的产量大于销量的情况。即在满足尽可能处理产生的垃圾量的条件下，还需最大化减少运输费用。这是一个线性规划问题，通过建立数学模型得到：

其中，xij为第i街道到第j中转站之间的垃圾运输量；cij为第i街道到第j中转站之间的运输费用；ai为第i个街道的垃圾产量；bj为第j个中转站的垃圾处理量；z即为整个运输过程中涉及的运输费用。约束条件右侧ai和bj为常数，约束条件最多有m+n-1个有效，该题则有23个，即最多有23个基可行解。为了能使用表上作业法，可增加一个假想的中转站B13，即相当于第一问中的再生资源处理厂，而由街道中心Ai（i=1，2，......，12）运输这个假想中转站的垃圾量xi，13（相当于松弛变量），实际上会就地存储在Ai。由于就地存储没有运输，故而不会产生费用，所以Ci，13=0（i=1，2，...，12）。令假想地的垃圾处理能力为：

据《T市生活垃圾处理的成本分析》汽车运费以1.5元／（t*km）计算。最后由表上作业法可得到一个总产量大于总销量，且销量全部满足的调配方案，最优方案见表3。

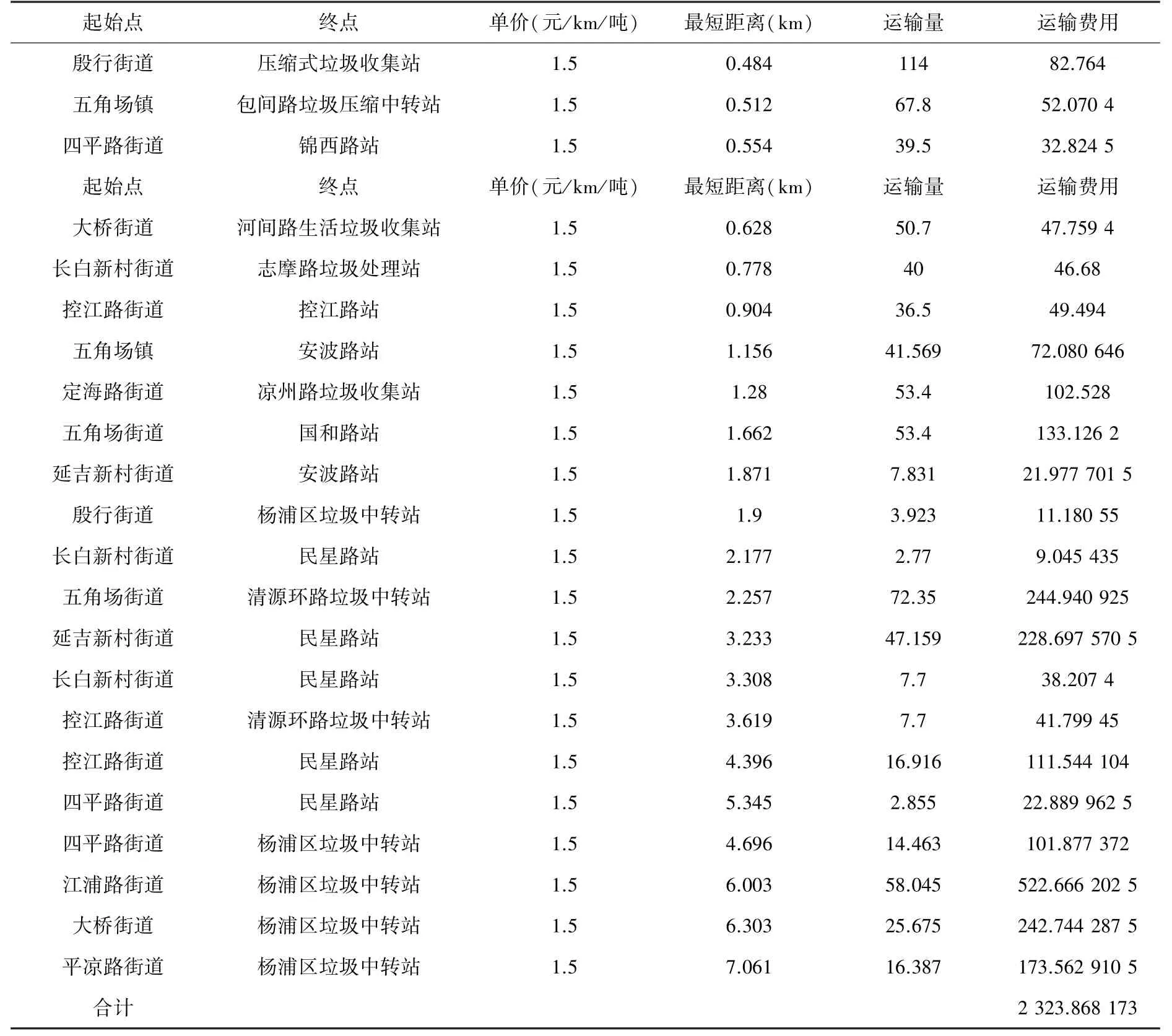
表3 运输路线Tab.3 Transportation route

由计算结果可知，大部分街道产生的垃圾量都是运送到距离其最近的中转站，更为方便和节省成本，这也是杨浦区政府报告中在各个街道内建设中转站的主要目的。此外也可以看出，新江湾城街道和平凉路街道所产生的垃圾量由于中转站处理能力有限，因而未能当日全部处理，会产生一定的存储费用，可见修建一处再生资源集散场迫在眉睫。

3 结束语

本文主要针对上海市杨浦区自实行垃圾分类后的垃圾管理与清运系统，对现行状况下的优缺点进行了分析。并在此基础上，分别对中转站以及各街道小区的日均垃圾处理能力与日均垃圾产生量进行对比后发现，现有中转站及其设施无法满足杨浦区每日垃圾收集量的处理，因而需要建设一处再生资源集散场。这样不仅能解决该问题，并且可以对所有可回收垃圾和部分干垃圾进行加工处理，得到二次产品。如此便在一定程度上降低了存储成本，同时增加了一项收入，并在一定基础上减缓了垃圾对环境的污染问题，方便了居民生活，改善了市容市貌，可谓一举多得。此外，运用重心法设计出了再生资源集散场的最佳位置，并在原有设施条件下改变了街道小区的垃圾仅送往附近中转站的垃圾处理方式。以运输成本最低为目标，运用表上作业法和线性规划得到最优垃圾清运路线。最后发现，大部分街道小区的垃圾运往附近中转站更为方便和节省成本，可见中转站地理位置的设计极为重要。但由于中转站能力有限，不能每日处理完居民产生的所有垃圾量，所以还是会产生一定的垃圾存储费用。由此可见，不仅需要再建一处设施供给垃圾处理，同时也须加大相关环保知识的宣传力度，以减缓相应费用，努力达到最佳环保效益和经济效益。