KNN 算法在高压直流输电单端故障检测的应用

（国网福建省电力有限公司 福建福州 350003）

0 引言

高压直流输电（HVDC）工程在电能输送、电网互联方面起着非常重要的作用。与高压交流（HVAC）输电技术相比，高压直流输电技术由于其灵活的控制能力和大电能的输送能力，在长距离输电、异步电网互联和可再生能源集成方面更具竞争力［1-2］。由于高压直流输电系统通常建设野外，所经过的路径远，可能经过特殊地形的环境等［3-4］，因此存在特定故障隐患。如何快速可靠地检测并排除故障，关系到整个高压直流输电系统的运行安全［5］。

传统的直流输电线路故障检测方法主要包括电压或电流差分方法和行波方法。Anderson［6］使用电压差率来检测线路故障，Li S 等［7］提出了一种新型的横向差动保护，利用差动电流和双端电流差动率来建立标准。蒋灵通等［8］通过前、后波头的准确检测，提出了基于时差的纵联方向保护。但是，差分方法受到故障电阻的影响很大，对波头提取要求极高，无法正确识别高阻故障。Ma Y 等［9］将行波保护应用于双回路传输线。Zhang Y 等［10］提出了一种基于零序和正序方向的行波保护方案，然而该方法容易受到干扰的影响，并且难以识别高阻故障。Kong F 等［11］通过单端数据分析反向行波的不同特性来实现故障检测。Luo S 等［12］提出了一种基于无功潮流的双端保护方案，可以在低采样频率下正常工作，但它需要两个时间延迟周期。

最近，有部分学者将机器学习的方法应用于电网保护。文献［13-14］通过人工神经网络（ANN）学习输入数据与目标值之间的关系，实现了交流配电系统小电流接地的故障保护。Johnson 等［15］使用支持向量机（SVM）来识别仅具有单端电压和电流信号的HVDC 故障线路。Chen M 等［16］将KNN 和SVM 作为HVDC 系统故障区域检测的分类机制。但是这些文献里面提到的方法尚未很好地解决启动组件的问题。李自乾等［17］通过公式推导消除行波波速的影响单端故障行波测距方法。郭敬梅等［18］结合故障条件中各因素对行波保护动作概率的影响程度，分析了运行方式变化带来的不利影响。文献［19-20］分析了KNN 在数据处理中具有良好的效率。张怿宁等［21］提出一种基于故障录波数据的耐受高阻接地的直流接地极线路故障测距新方法。

目前，关于HVDC 故障检测的研究，大部分选取的接地电阻均小于500 Ω。但在实际运行的电力系统，有的故障类型故障电阻比这个值高，甚至达数万Ω。因此，在采样频率尽可能小的前提下，增加检测系统的可测量电阻值上限是迫切需要解决的难题之一。

本文将K 最近邻（KNN）引入高压直流输电系统，利用KNN 优秀的分类性能与小样本训练能力实现HVDC 系统快速故障检测。本方法的采样频率为10 kHz，整流侧检测装置采集到故障信号后直接作为KNN 模型的输入，训练好的KNN用于检测故障区域，用PSCAD/EMTDC 建立高压直流输电模型，仿真结果表明该方法可以成功识别电阻高达1 000 Ω 的故障。本文介绍了所提出的故障检测方法的基本原理，与基于反向行波的故障检测方法进行了比较，并通过电磁暂态仿真软件PSCAD/EMTDC 搭建±500 kV 高压直流输电系统，在不同故障区域与故障类别下对所提出方法的有效性进行评估验证。

1 KNN 故障检测方法

高压直流输电系统HVDC 包括：双端交流系统、整流器、逆变器和输电线路。线路边界由直流滤波器和平滑电抗器组成，起到低通滤波的作用。无论直流输电系统哪个部分发生故障，整流器侧检测装置都将检测到电压突变。由于线路边界和线路阻抗的影响，不同区域的故障波形将具有不同程度的幅度和平滑度。基于K-Nearest Neighbor（KNN）的故障检测方法，流程图如图1 所示。整流侧检测装置检测到电压突变后启动检测算法，采集到的故障波形通过事先训练好的KNN 判断器诊断是否为接地故障或者双极短路故障。若KNN 判断器诊断为是，则再由KNN 分类器区分故障为内部故障或者为外部故障以及故障发生在哪条输电线路上。两个KNN 均由各种故障区域和故障条件下采集到的电压大量训练，训练好的KNN 用于实现故障检测。

图1 KNN 方法流程图

1.1 KNN 算法

K-Nearest Neighbor（KNN）是一种监督学习分类器。作为经典分类算法之一，其核心思想包含未知样本的空间中，如图2 所示，可以根据最近邻k 个样本的数据类型确定样本的数据类型。KNN 有三个主要因素：训练集、距离和类似度量、以及k值［16，22］。

图2 KNN 示意图

对于一个测试样本，需要计算该测试样本与训练集中的其他样本之间的关系程度。不同的数据集拥有对应的最佳距离函数，常见的距离函数分别有：

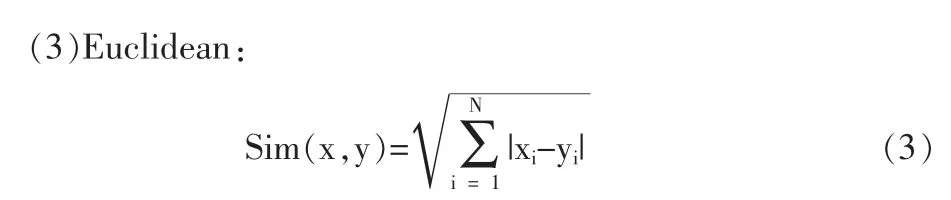
式中：特征向量S 表示协方差矩阵，Si是第i 维度中的样本数据的标准偏差。首先，使用初始值确定k 值，然后根据实验测试的结果调整k 值。其次，根据样本的相似度，在训练集中选择与测试样本最相似的k 个样本。在k 个最近邻样本中，计算每个类别的权重，并通过比较权重将样本分类到具有最高权重的类别［23］。

1.2 KNN 判断器和KNN 分类器

受到文献［24］的启发，本文搭建两个KNN 模型。第一个KNN 为判断KNN，其作用是当检测装置采集到突变波形后，判断该波形是否为接地故障或者为双极短路故障。其中x 是测试样本的特征向量，y 是训练集的。利用这个KNN，在保证整个检测方案快速启动的前提下还能确保不会发生误启动。第二个KNN 为分类KNN，利用KNN 优秀的分类机制实现线内外故障的区分以及确定故障线路，这个KNN 也是整个检测方案的主体部分。

本文搭建两个KNN 模型，这两个KNN 模型的基本参数相同。考虑到特征数据的差异性，本研究的KNN 模型采用“Mahalanobis”距离函数，该函数能够考虑到各种特征量之间的联系并准确提取变量间的微小变化。考虑到不同的k 值对训练结果具有不同的影响，表1 显示了两个KNN 模型中不同k 值的训练结果。在HVDC 系统中，两个KNN 模型对k 值的敏感度一致，其训练和测试数据精度都是随着k 值的增加而减少，因此本文中两个KNN 模型的k 值都取1。两个KNN 模型之间的区别在于类别N 的取值不同。对于判断KNN，将N 值取为2 以确定它是否是接地故障。对于分类KNN，N 值取4用以实现故障部分和故障线路检测。

1.3 启动组件和采样窗口

在本文研究中，直流电压差du/dt 直接用于故障检测的启动标准。然而，包括电压导数方法在内传统方法存在诸如负载波动导致检测系统误激活的缺陷。因此KNN 方法在启动根据DC 电压差提取电压波形，然后再使用训练完的KNN 来确定它是否为接地故障或双极短路故障。

采样时间窗口的选择将严重影响整个检测方案的性能，故障条件下检测到更长的波形意味着不同区域故障之间的差异更加明显，所以波形采样窗口应尽可能长。但是瞬时性是电力系统故障保护的重要因素，这就要求采样窗口尽可能短。本文通过PSCAD/EMTDC 在不同故障距离和因素下进行模拟，在采样频率为10 kHz 的条件下选择100 个采样点（10 ms）作为采样窗口。对于交流侧故障，这个采样窗口可以采集到5 个周期的故障波形。对于线路故障，在输电线路全长为800 km 假设行波波速为2.95×108m/s 的情况下，该采样窗口足以采集故障行波在输电线路上两个来回的信息。传统的保护方案采样窗口基本都有周期时间延迟，而不少新提出的方案采样窗口也都在5 ms 以上［11-12］。本文所提出的检测方案采样窗口为整流侧检测装置检测到电压突变电的前19 个采样点以及后80 个采样点，在确保保护精度的前提下更符合故障保护瞬时性的要求。

表1 不同k 值对训练效果的影响 %

通过PSCAD/EMTDC 在不同故障区域和条件下进行模拟，采集整流侧的故障电压波形，这些一维特征波形就是KNN 的训练样本和测试样本。瞬时性是故障检测算法的基本要求。研究用的计算机处理器RAM 和处理系统分别为4.00GB 和IntelcoreTM i5-3230 CPU ＠ 2.60GHZ。整个故障检测算法的启动组件运行时间为0.038 1 s，KNN 分类程序运行时间为0.041 0 s，完全满足故障检测瞬时性的要求。

2 对比方法

为了和KNN 方法进行最直接的比较，借鉴Kong 等［11］提出的方法，将反向行波应用于HVDC 故障检测。线路外部故障的行波示意图如图3 所示，M 代表线路整流侧，N 代表逆变侧。输电系统整流侧外部发生故障的行波传播过程如图3（a）所示，在时间间隔［t0，t0+2l/v］内，线路内部只存在前向行波uf，而反向行波ub=0。因此整流侧检测装置采集到的电压信号仍然维持平稳。如图3（b）所示，当逆变侧外部发生故障时，整流侧检测装置采集到的初始行波是从逆变侧传导过来的反向行波ub。因此，在时间间隔［t0，t0+2l/v］内，检测装置能够检测到一个突降的反向行波。

图3 线路外部故障行波示意图

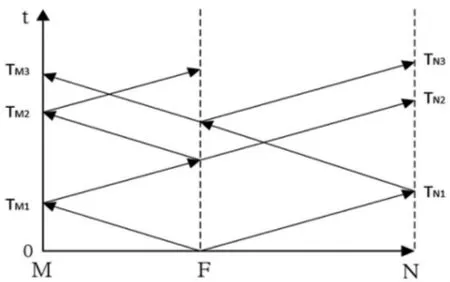
图4 线路内部故障行波示意图

线路内部故障的行波示意图如图4 所示。在时间间隔［t0，t0+2l/v］内整流侧检测装置能够多次检测到不同行波波头，如图中TM1、TM2、TM3…。由于极短时间内不同波头的抵达，检测到的故障电压含有高频震荡分量。这使得线路内部故障与线路外部故障存在显著差异。

当检测到线路内部故障后，反向行波法利用采集到的电压故障分量的数字特性识别故障线路。当正极线路短路时，故障点可视为一个对地的负电源，它将造成的整流侧电压Δu＜0。而对于负极接地故障，整流测正极采集到的电压震荡且无法保持Δu 负极性稳定。

3 仿真系统和实验结果

3.1 仿真模型和参数

利用PSCAD/EMTDC 电磁暂态仿真软件建立仿真模型。本研究基于PSCAD/ EMTDC 中提供的CIGRE 基准模型，建立了标称电压为500 kV、额定传输功率为1000 MW 的HVDC 输电系统。一般通用的高压直流系统的单线结构如图5 所示［16］。

在该模型中，每个转换器都有两组12 脉动转换器，整流侧控制系统采用定电流控制和最小触发角控制，逆变侧控制系统采用定熄弧角控制、定电流控制和电流偏差控制，整流侧和逆变侧都装有抵押限流控制VDCOL（Voltage Dependent Current Order Limiter）。系统和变压器详细参数见表2 和表3。

表2 高压直流输电系统详细参数

表3 变压器详细参数

图5 高压直流输电系统单线结构图

3.2 故障区域仿真

故障检测实验是在不同的故障条件和因素下进行的，包括不同的区域、不同的接地电阻和不同的输电线路。通过整流侧检测装置M 收集故障发生后的前半周期（100 个采样点）电压波形。

HVDC 输电系统中只有两条传输线，因此线路故障的类型不像交流系统那样多样化，单线接地故障（正接地，负接地）最为常见［15］。双极输电线路短路故障较为少见并且很难识别［25］。如图5 所示，将HVDC 系统的故障区域和类型划分为F1-F6：整流侧交流系统接地故障，逆变器侧交流系统接地故障，整流器端口故障，逆变器端口故障，正极输电线路接地故障，负极输电线路接地故障和双极短路故障。其中，F1-F3为线路外部故障，双端交流系统故障统一为交流系统故障。交流系统故障设置为单相接地故障。HVDC 系统不同区域的故障模拟结果如图6 所示，故障时间设定为1.0 s。

图6 HVDC 系统不同区域故障仿真

图6（a）为整流侧和逆变侧的交流系统故障电压波形。故障类型为A 相金属接地。整流器侧的电压波动幅度大于逆变器侧的电压波动幅度，但两者的电压波动范围不是很大。图6（b）表示在整流器和逆变器端口中发生接地故障之后的电压波形。与交流系统故障的小幅波动不同，整流器或逆变器发生故障会导致电压急剧下降。图6（c）是输电线路内三种不同故障类型的电压波形。故障类型皆为金属接地故障。可以看出，输电线路内部和外部故障波形完全不同，它会导致电压大幅度波动并且波动频率很高。

3.3 训练数据

在PSCAD/EMTDC 电磁暂态仿真软件中，整流侧检测装置采集到故障电压波形（突变点前19 个采样点和后80 个采样点）。这些故障波形直接作为KNN 模型的训练样本和测试样本。

考虑高压直流输电系统故障影响因素和区域的多样性，本文在HVDC 系统6 个区域（F1-F6）分别设置了0～1 000 Ω 的故障接地电阻。基于KNN 小样本训练的优越特性，每个区域共设置30 笔故障。KNN 判断器训练集共包含2 个种类，每个种类包含180 笔数据，而KNN 分类器包含4 个种类，每个种类包含30 笔数据。本文所设置的故障接地电阻从低到高涵盖不同阻值范围，并且对HVDC 所分割的6 个故障区域涵盖系统的所有元件，保证了训练样本的广度和深度。

3.4 测试数据

为了验证本文提出的基于KNN 方法以及基于反向行波法的准确性，测试实验的数据集考虑了不同于KNN 的训练样本。本文将故障电阻小于200 Ω 的故障类型归为低阻接地故障，将故障电阻大于200 Ω 的故障类型归为高阻接地故障。

为了更好的展现各个方法的性能，本文引入准确度（φ），其计算方法如下：

表4 和表5 显示了低阻接地故障和高阻接地故障情况下两种方法的测试结果。“Fault section”表示线内故障和线外故障，Fx 表示故障区域，“Sample number”表示在每个故障区域中测试的样本数。由于反向行波法无法准确检测双极短路故障，因此测试实验忽略此项目。

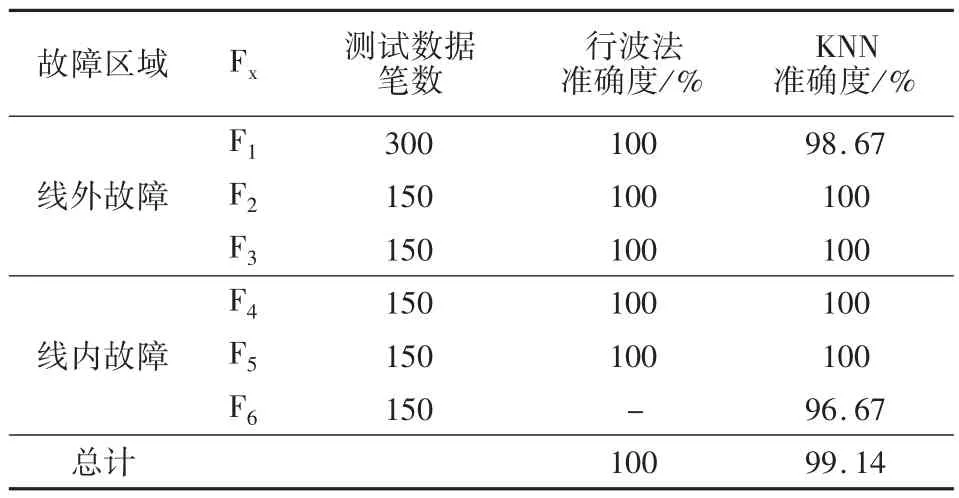
表4 低阻接地故障检测结果

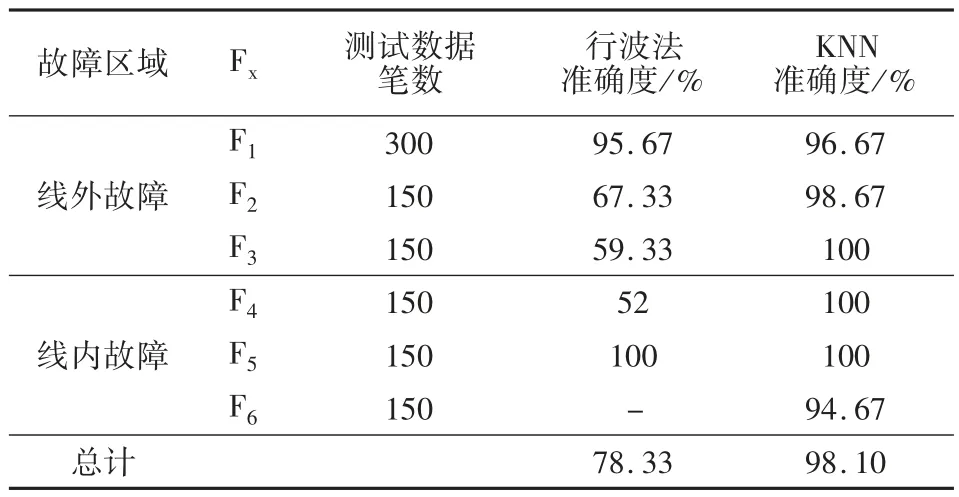
表5 高阻接地故障检测结果

测试结果表明，反向行波法在低阻故障情况下具有极其优秀的检测能力，检测精度甚至超过基于KNN 的故障检测法，但是在高阻故障情况下它的检测精度并不理想。这是由于随着故障电阻的增加，行波波头将变得难以获取，这也是行波法的通病。反观KNN，无论是低阻接地还是高阻接地故障，基于KNN 的检测方法都具有良好的识别能力。虽然该方法可能会产生轻微误判，但它们的准确性仍然足以满足实际工程应用的要求。因此，基于KNN 的故障检测方法可以实现1 500 Ω以内的故障电阻识别。

3.5 抗干扰测试

电力系统正常运行时，负荷、发电机和调节系统的变化经常会造成系统电压不同程度的扰动，为了使仿真实验更贴近实际工程，本节在模型中引入2%、5%两种不同程度的基准电压扰动，并测试在这两种干扰信号下，基于KNN 故障检测方法的抗干扰特性。实验结果如表6。

表6 KNN 方法抗干扰测试 准确度（%）

可以看出不论在何种扰动情况下，基于KNN 的故障检测方法都能保持一个极高的检测准确精度。即使扰动水平达到5%基准电压，故障电阻达到1 500 Ω，所提出的方法的检测准确率仍达到97.24%，这完全满足实际工程的要求。

高压直流输电系统稳定运行时会存在微小干扰信号（视具体线路而定），但干扰达到甚至超过5%基准电压水平的情况微乎其微。因此基于KNN 的故障检测方法具有极高的抗干扰稳定性。

3.6 线路故障检测

在电力系统故障检测方案中，能否确保输电线路全长的准确检测是一个关键的评判因素。为了验证该方法的可靠性，在全长800 km 的输电线路上，分别在0.1 km 到799.9 km 之间设置不同故障类型，测试结果如表7 所示。表7 的结果表明，即使故障距离发生变化，该方法也能确保输电线路全长的准确故障识别。

表7 不同输电线路距离的故障检测结果

3.7 讨论

从上述测试结果可以看出不论是低阻故障还是高阻故障，本文所提出的基于KNN 的故障检测方法都具有优秀的识别精度且优于传统行波法。该方法有效提升高压直流输电系统故障接地电阻的测量范围，不论在什么故障区域、条件下，都能够实现1500 Ω 故障的准确可靠识别，并且通过抗干扰性分析验证了本方法具有较高的稳定性。

从表5 中可以看出当故障电阻达到一定程度后，传统行波法将产生较大误判。这是由于随故障电阻升高，不同区域的电压波形变化幅度将减小。以200 Ω 接地故障为例，如图7 所示。图7（a）为线路外部区域故障电压波形，图7（b）为线路内部故障电压波形。按照Kong 等［11］提出的反向行波法很难通过设置阈值等方式区分逆变侧端口故障或者负极短路故障，并且由于负极短路故障和双极短路故障的电压波形极为相近，因此反向行波法也很难识别双极短路故障。而KNN 能够通过对距离函数、k 值的选取使得模型对各个故障类别具有优秀的分类能力。只要确保训练样本的代表性，基于KNN 的故障检测方法可以实现大电阻接地的准确检测。

图7 高阻故障条件下不同区域电压波形

4 结论

本文提出的基于K-最近邻的HVDC 单端故障检测方法，可以准确检测HVDC 输电系统中的高阻故障的区域和线路，整流侧采集的故障电压用于所提出的KNN 模型的训练数据。训练后的KNN 模型用于检测故障区域。还列出了基于反向行波的故障检测方法解决上述问题。通过PSCAD/EMTDC 软件进行仿真，验证两种方法的可行性。测试结果表明，相比方向行波法，基于KNN 的高压直流输电系统故障检测方法可以提高故障检测性能并实现故障电阻高达1 500 Ω 的特殊故障区域的准确检测。