MapReduce 框架下结合分布式编码计算的容错算法

张 基，谢在鹏，毛莺池，徐媛媛，朱晓瑞，李博文

（河海大学计算机与信息学院，南京 211100）

0 概述

容错技术是分布式系统的重要组成部分，确保了发生故障时的系统连续性和功能性［1］。近年来，随着分布式系统规模的不断扩大、分布式架构和计算复杂度的日益增加［2］以及廉价商业硬件的广泛使用，使得计算任务发生故障的概率持续增加，例如在Google 生产集群中平均每天会有数十个节点发生故障［3］。瞬态故障尤其是软错误［4］会导致计算机系统的异常行为，这类故障会损坏数据的完整性，引起分布式节点的计算失效［4-5］。在一些大型分布式系统中平均每天会有1%～2%的节点发生失效［6］，因此容错技术可在保证部分节点失效的情况下，使分布式系统仍能继续运行且得到正确结果［7-9］。在基于MapReduce［10］的分布式计算中，数据洗牌（shuffle）阶段较高的通信开销严重影响了分布式计算性能，例如在Facebook 的Hadoop 集群中，33%的任务执行总时间用于数据洗牌阶段［11］。针对基于MapReduce 分布式计算框架的多副本容错算法通信开销较大的问题，本文提出一种结合分布式编码计算的容错算法CTMR，使基于MapReduce 的分布式计算系统在发生瞬态故障的情况下仍能继续运行且得到正确结果，同时能有效降低容错计算过程中的通信开销。

1 相关工作

基于多副本冗余技术［12-15］的分布式容错算法于1962年由IBM提出，但在现代分布式系统中仍然被广泛采用［16-17］。这类算法的主要思想是：在含有n个节点的分布式系统中，如果每个节点要容忍f个故障，那么该节点可以使用（f+1）个独立的副本，显然存储和运行这些副本需要消耗大量的空间和其他资源。此外，由于多副本之间的一致性使得基于副本冗余技术的容错算法更易于设计，同时副本的维护和恢复成本较低。三模冗余（Triple Modular Redundancy，TMR）是软件和硬件系统中常用的基于副本的容错算法［18-19］，使用3 个实现功能相同的模块同时进行操作，系统使用投票机制选出最终输出。由于3 个模块相互独立，同时有2 个模块出现相同错误的概率非常小，因此可大幅提高系统可靠性，掩蔽故障模块的错误。文献［20］提出一种优化的副本虚拟机放置算法，动态设置k个副本虚拟机并将其作为备份来提高云服务的可靠性。在基于MapReduce的分布式计算［10］中，每个任务被分配到多个节点以确保在某个节点出现故障的情况下系统仍能继续运行。文献［21］提出面向分布式流体系结构的多副本容错技术，该技术通过比较多个副本的数据进行检错，采取三取二的逻辑判断方式选择多数相同的结果，并对错误的数据进行纠错以防止错误进一步传播，但当数据量较大时通信开销会成为容错过程中的性能瓶颈。文献［18］提出一种两阶段三模冗余（two-stage TMR）容错算法，该算法将每个任务备份3 份并分配给3 个节点，先指定2 个节点进行计算，当2 个节点执行完毕后进行结果比较，如果比较结果不一致，则指定第3 个节点进行计算，最终通过投票选出多数一致的结果。该算法在故障率较低的情况下可以有效节省系统资源，但当错误率较高时，重新执行第3 份备份任务不仅增加了计算工作量并且大幅降低了系统实时性能。

通信开销是基于MapReduce 的分布式计算中的主要性能瓶颈，这是因为在数据洗牌阶段交换大量中间结果。为解决该问题，文献［7］提出分布式编码计算方法，将map 任务重复布置到多个不同的节点，通过增加计算冗余创建同时满足多个服务器数据需求的编码数据来降低通信开销。在一个分布式集群中，node1包含数据集{v1，v2}，node2包含数据集{v2，v3}，node3包含数据集{v1，v3}。node1将本地数据集编码结果c1（c1=v1⊕v2，⊕表示异或）运用广播发出。node2接收到编码数据后利用本地数据v2即可将收到的编码结果解码得到v1，其中v1=v2⊕c1。同理，node3通过解码即可得到v2。在该过程中，通过将node1与node2和node3冗余存储的数据{v1，v2}进行编码来创建同时满足node2和node3的编码数据，而无需将v1、v2分别发送至node2和node3，从而降低通信开销。然而，目前尚未发现能有效降低分布式容错计算中通信开销的相关讨论和研究。为降低现有分布式计算使用多副本容错过程中产生的通信开销，本文基于副本冗余和分布式编码计算技术，提出一种CTMR 容错算法。

2 CTMR 容错算法

2.1 CTMR 模型

假设在分布式集群中有N个节点，标记为{node1，node2，…，noden}，N个节点协作完成一个计算任务。当前集群待处理的数据量为M，每份数据的冗余度为r，将该数据集分配到当前集群的N个map节点，每个节点的数据量为M⋅。map 节点对数据进行计算，将产生的中间结果使用分布式编码计算得到的编码数据发送到Q个reduce 节点，其中编码压缩比为c，即将c个中间结果通过编码得到一个编码中间结果。因此，每个reduce 节点将收到其余（N−Q）个map 节点的编码中间结果，如式（1）所示：

reduce 节点对接收到的编码中间结果进行解码，通过校验识别发生故障的编码数据包，并利用冗余中间结果得到M份数据最终正确的计算结果，如式（2）所示：

因为本文算法随机选取Q个reduce 节点均能够完成所有中间结果的验证，所以节点应该包含编码数据所有可能的中间结果，如式（3）所示：

由于TMR 的低复杂度及高可靠性，因此本文选取r=3、c=2，联立式（1）～式（3）解得N=6、M=8，即在含有6 个节点的分布式集群中，将待处理的数据分成8 个独立的子数据块，每个数据块冗余3 份，每个节点包含4 份数据，使用故障检测与恢复算法进行容错计算，同时降低计算过程中的通信开销。

在包含N个节点的分布式集群中，将每6 个节点分为1 个子集群，共有组子集群。各个子集群之间相互独立，而每个子集群内的节点在逻辑上是相邻的，在物理上可以是分散的。将计算任务分配到个子集群上，各个子集群并行计算。每个子集群的数据量为，同时将子集群的数据集划分为8 个独立的子数据块，每个数据块复制3 份。每个子集群使用如图1 所示的CTMR 模型进行表示，其中立方体的每个面表示1 个节点，每个面的4 个顶点代表当前节点包含的4 个数据集。立方体中的每条棱代表与该棱邻接的两个面所表示的节点公共冗余数据集，而每个面所表示的节点数据集用Bi表示，例如node1本地数据集为B1={b1，b2，b3，b4}。在模型中每个顶点与3 个面邻接，即每份数据冗余3 份并存放至3 个节点上，例如b3分别存放至node1、node3和node5上。nodek在map 阶段对本地数据集的每一个数据块bi执行map 函数F(bi)得到相应的中间结果集。

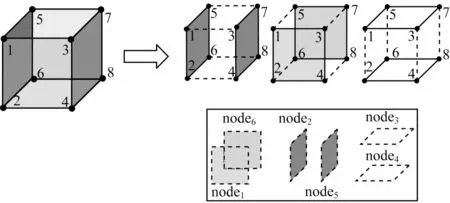
图1 CTMR 模型Fig.1 CTMR model

两个邻近节点nodek和nodem冗余存储的数据集用Rk，m表示，例如R1，3={b1，b3}。将nodek与nodem冗余存储的数据Rk，m所对应的中间结果使用分布式编码计算得到编码结果uk，m，如式（4）所示：

其中，⊕表示异或操作。nodek在reduce 阶段的函数为H(v1，v2，…，vi)=rk。

2.2 CTMR 故障检测与恢复

将一个包含N个节点的分布式集群划分为个子集群，各个子集群并行计算的同时进行检错和纠错。每个子集群中的6 个节点分别表示为nodek、nodem、nodes、noden、nodep、nodeq，其中nodek和nodem、nodes和noden、nodep和nodeq分别为CTMR模型中的3 组对面。可以看出，任意一组对面中的两个节点的本地数据集的交集为空，但并集是当前子集群数据集的全集。每个节点map 阶段通过函数F(bi)计算本地数据集得到相应的中间结果集，例如nodek通过计算本地数据集Bk得到相应的中间结果集。

随机选取一个节点nodek，将其在CTMR 模型中的对面节点nodem作为校验节点。nodes、noden、nodep、nodeq为与nodek相邻的节点，将其与nodek冗余存储的数据集Rs，k、Rn，k、Rp，k、Rq，k所对应的中间结果进行编码，得到相应的编码结果us，k、un，k、up，k、uq，k。将对应的编码结果发送给nodek，然后在nodem上执行相同过程。数据块分发与中间结果编码的伪代码如算法1 所示。

算法1数据分发与中间结果编码算法

nodek和nodem通过比较接收到的编码数据包与当前节点产生的中间结果来验证数据的正确性。若式（5）两个等式中的任意一个成立，则表明nodek本地数据集的运算结果正确，通过reduce 函数可得到当前节点运算结果。

若式（5）中两个等式均不成立，而式（6）两个等式中的任意一个成立，则假设us，k验证成功，即us，k=

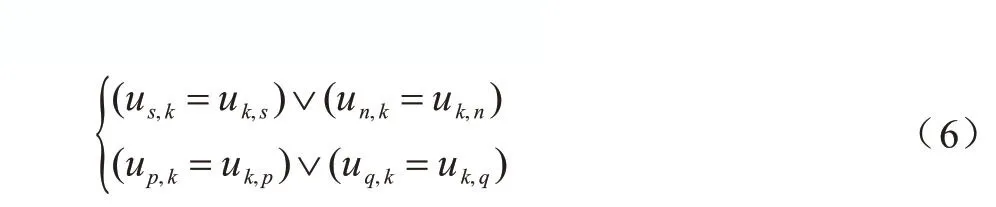
若式（7）成立，则表明nodek本地有数据计算错误，但是收到的其他节点的编码数据包正确。此时，通过reduce 函数得到当前节点数据集的正确结果为

若us，k、un，k、up，k、uq，k全部验证失败，则重新选取两个校验节点进行上述操作。当nodek与nodem均能通过验证得到正确运算结果时，利用reduce 函数便可得到CTMR 模型的最终结果r=H(rk，rm)。故障检测与恢复的伪代码如算法2 所示。

算法2故障检测与恢复算法

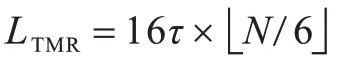
在随机选取子集群中的两个reduce 节点后，每次TMR 算法验证都需发送16 份中间结果给reduce 节点，假设每个中间结果大小为τ，那么每个CTMR 模型在验证过程中需要发送16τ的数据。在含有N个节点的分布式集群中，共需发送的数据量。two-stage TMR 算法在最优情况下只需发送8τ的数据量，即最初选择的两个副本对应的中间结果一致，在最坏情况下所有数据最初选择的两个副本的对应中间结果均不一致，因此需要第3 个副本进行多数一致表决，共需发送16τ的数据量。在CTMR 算法中，每个节点使用分布式预编码本地计算的中间结果减少通信开销。在最优情况下，每个模型只需8τ的通信量，即模型最初选择两个校验点即可得到正确结果。在最坏情况下，每个模型需要16τ的通信量，即在最初选择两个校验节点后不能得到正确结果，需更换节点重新做校验。因此，在包含N个节点的分布式集群中，共需发送的数据量。CTMR算法与TMR算法的通信开销之比如式（8）所示，即CTMR算法总能在小于等于TMR 算法通信量的情况下得到正确结果。

2.3 算法实例

如图2 所示，在含有N=6 个节点的分布式集群中，输入系统数据量为M=8，将该数据集划分为8 个数据块{b1，b2，…，b8}。每个节点在map 阶段计算本地数据集产生相应的中间结果集，例如node2在map 阶段针对本地数据集B2={b1，b2，b5，b6}计算得到相应的中间结果集。考虑node1在map 阶段由于瞬态故障导致计算错误情况下的容错过程，首先选取node1和node6作为校验节点，子集群中其余4 个节点为node2、node3、node4、node5，将4 个节点与node1冗余存储的数据集R2，1、R3，1、R4，1、R5，1所对应的中间结果分别使用分布式编码计算得到相应的编码结果u2，1、u3，1、u4，1、u5，1发送给node1，将4 个节点与node6冗余存储的数据集R2，6、R3，6、R4，6、R5，6所对应的中间结果分别使用分布式编码计算得到相应的编码结果u2，6、u3，6、u4，6、u5，6发送给node6，其中，。

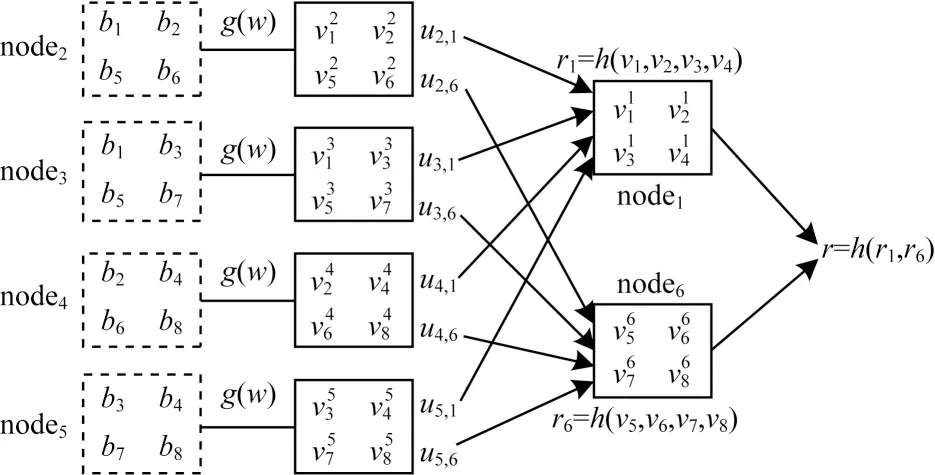
图2 node1中 和 错误时的容错过程Fig.2 Fault-tolerant process of and incorrect in the node1

3 实验结果与分析

3.1 实验方案

本文分布式计算的测试程序为Terasort［22］，CTMR算法的评价指标为任务执行总时间、map 和shuffle 阶段执行时间以及平均故障修复时间（Mean Time to Repair，MTTR），对比算法为TMR 和two-stage TMR算法。

实验使用多台虚拟机搭建的分布式集群，包括1个管理节点和6 个工作节点，节点间的带宽为100 Mb/s。实验中动态选择发生故障的节点个数，随机选取节点并修改其对应数据块数值实现故障注入。假设系统在单位时间内的故障发生概率服从泊松分布p(x=k)=，即在单位时间内出现k个故障的概率为p(k)，本文中λ的取值为2。因此，在满足泊松分布的条件下，假设该分布式系统随机产生k个故障。如果各个故障之间相互独立，那么在连续运行的分布式系统中，当产生k个故障时的无故障运行时间为tk，则系统平均无故障运行时间如式（9）所示：

故障修复时间为检测到故障直至故障修复的时间，假设有k个故障时的故障修复时间为θk，则平均故障修复时间如式（10）所示：

实验中每个MapReduce任务可以分为map、shuffle、check 和reduce 这4 个阶段。在map 阶段，管理节点按照CTMR 算法要求将用户输入数据分发给6 个工作节点，同时指定2 个校验节点。每个工作节点对本地数据集进行排序，得到相应的中间结果集。在shuffle 阶段，每个节点将其中间结果编码，发送给之前指定的校验节点。在check 阶段，校验节点将收到的数据包进行故障检测和恢复，校验成功后得到相应结果。在reduce阶段，管理节点收到校验节点发送来的部分reduce 计算结果后执行reduce 函数得到最终输出结果。任务执行总时间Ttotal如式（11）所示：

3.2 实验结果

图3 给出了CTMR、two-stage TMR 以及TMR 算法的任务执行总时间对比结果。可以看出，CTMR算法能有效降低分布式计算的任务执行总时间。当故障个数较少时，CTMR 算法的执行效率远高于另外两种算法。随着故障个数的不断增加，two-stage TMR 算法由于需要重新执行第3 个副本做验证，而CTMR 算法则需要更换节点做验证，在该过程中需要重新发送编码数据包，因此这两种算法的任务执行总时间也会随之增加。

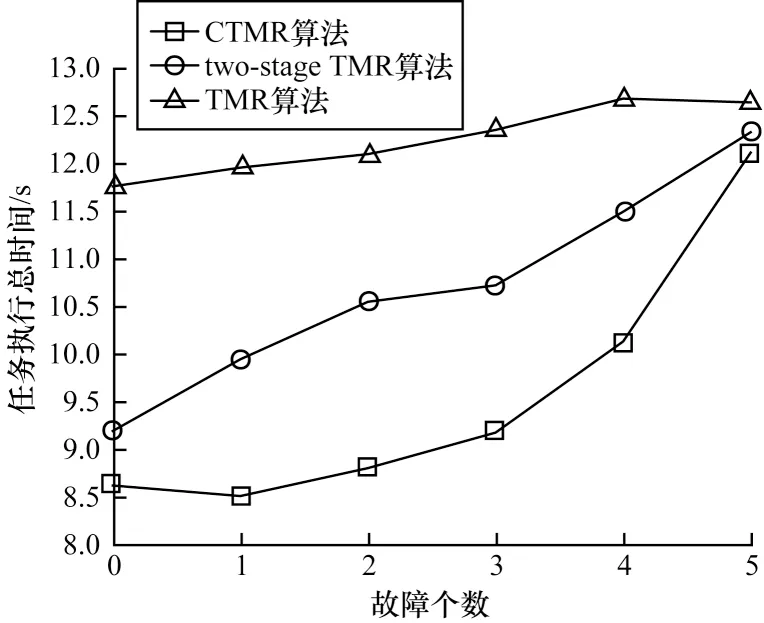
图3 任务执行总时间对比Fig.3 Comparison of total task execution time

图4 给出了CTMR、two-stage TMR 以及TMR 算法在map 阶段的执行时间对比结果。可以看出，随着故障个数的增加，two-stage TMR 算法由于第1 次投票选择的2 个副本对应的中间结果不同，因此需要进行第2 次投票。这时会选择第3 个副本并执行map 任务，因此map 阶段所需时间随故障个数的增加不断增加。TMR 和CTMR 算法由于最初都要对3 个副本执行map 任务，因此map 阶段的执行时间基本保持不变。

图4 map 阶段执行时间对比Fig.4 Comparison of the execution time in the map phase

图5 给出了CTMR、two-stage TMR 以及TMR 算法在shuffle 阶段的执行时间对比结果。可以看出，CTMR 算法在shuffle 阶段所需时间明显低于TMR算法，并且相比two-stage TMR 算法有一定程度的减少。本文将shuffle 阶段的执行时间作为通信开销的衡量指标，当系统在单位时间内的故障发生概率服从泊松分布时，可以计算得出发生k个故障的概率为p（k），本文中λ的取值为2。根据式（9）可计算出CTMR、two-stage TMR 以及TMR 算法在shuffle 阶段的执行时间分别为1.90 s、2.21 s 和3.22 s。因此，CTMR 算法在shuffle 阶段的执行时间相比TMR 算法降低了41.0%，相比two-stage TMR 算法降低了14.0%。

图6 给出了CTMR、two-stage TMR 以及TMR 算法在check 阶段的执行时间对比结果。可以看出，CTMR 算法在一定的故障个数范围内，故障修复效率明显优于TMR 与two-stage TMR 算法。随着故障个数的不断增加，TMR 和two-stage TMR 算法均需要对所有副本进行第3 次投票，而CTMR 算法也需要更换节点进行校验，因此3 种算法的故障恢复时间不断增加并最终趋于一致。

图6 check 阶段执行时间对比Fig.6 Comparison of the execution time in the check phase

当系统在单位时间内发生故障的概率服从泊松分布时，根据式（9）分别计算出CTMR、two-stage TMR 以及TMR 算法在tatal 阶段的任务执行总时间以及map、shuffle 和check 阶段的任务执行时间，结果如图7 所示。可以看出，CTMR 算法的任务执行总时间相比TMR 算法降低了25.8%，相比two-stage TMR 算法降低了13.2%。根据式（10），CTMR 算法的平均故障修复时间相比TMR 算法降低了18.3%，相比two-stage TMR 算法降低了26.2%。

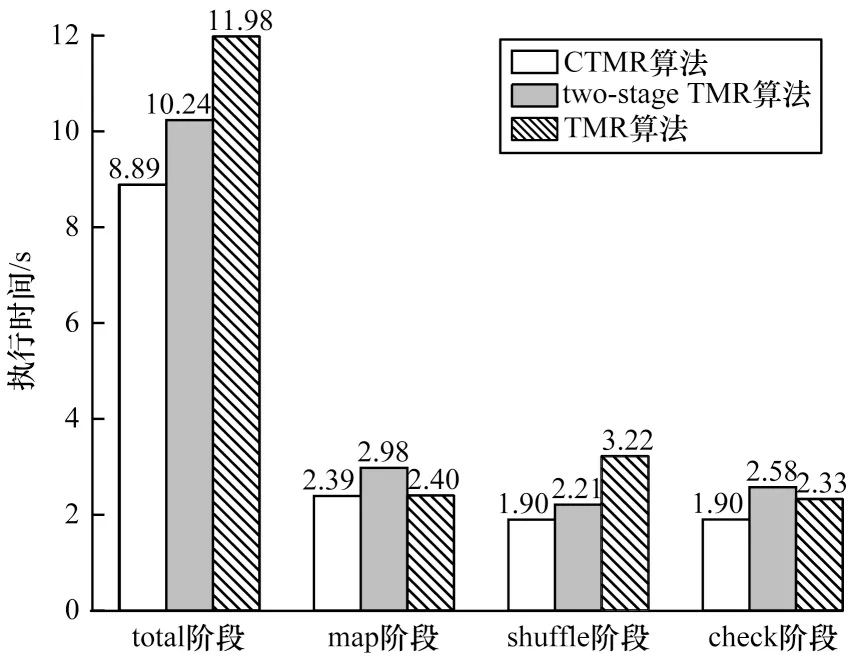
图7 故障发生概率服从泊松分布时3 种算法的执行时间对比Fig.7 Comparison of the execution time of the three algorithms when the probability of failure obeys the Poisson distribution

4 结束语

为降低MapReduce 分布式计算中容错算法的通信开销，本文结合副本冗余技术和分布式编码计算技术，提出一种新的容错算法。实验结果表明，CTMR 算法在完成容错计算的同时，相比TMR 和two-stage TMR 容错算法，平均降低了41.0% 和14.0%的shuffle 阶段的通信开销以及18.3%和26.2%的平均故障修复时间，并且提高了分布式系统的可用性和可靠性。但由于本文中的副本数量固定为3具有一定的局限性，因此下一步将根据分布式系统的故障发生概率，通过动态调整副本数量以增强容错算法的灵活性。