基于权重优化神经网络的盾构机掘进参数预测方法

牟 松，段文军，庄元顺，刘绥美，章 峰

（1.中铁工程服务有限公司，四川成都610083；2.电子科技大学计算机科学与工程学院，四川成都611731）

目前盾构机的运行状况分析主要取决于决策人员的经验判断，而在工程进行过程中，决策人员难以对复杂的信息和数据进行快速而准确的分析，并且这种凭借工程经验进行参数调节的方法对于不同地质条件下的挖掘效率不能保证。

为了改善上述情况，很多学者对如何高效优质地完成盾构施工这一问题进行研究，并有了一定的研究成果。崔福义等［1］基于杭州地铁1 号线盾构法施工工程，调整隧道结构施工事故预防和处理措施的设计，有效保证盾构机的顺利掘进。倪振利［2］运用辅助决策系统实现了对施工过程中的优化控制。李守巨等［3］根据盾构机掘进的历史观测数据，提出了盾构机掘进决策支持系统。然而，受地质条件、线路设备、工程状况等影响，相对于理论情况，实际的工程状况更加复杂，需要加强模型的泛化能力。

同时，基于机器学习的盾构机参数预测方法已经成为一个研究热点，相较传统方法更为准确。周斌等［4］和陶冶［5］通过应用支持向量机算法，建立了复合地层盾构机推进速度的预测数学模型，提高盾构机的工作效率。丁海英［6］提出了盾构掘进参数类比设定法，通过对历史的数据进行聚类，实现了对掘进参数的提取和自动匹配。郝用兴等［7］通过将差分进化算法与神经网络算法（Back Propagation，BP）相结合，对盾构机推进液压系统进行故障诊断。王传俭［8］和徐进等［9］利用人工神经网络，对盾构机的掘进参数和掘进过程中地表的沉降进行预测。付耀琨［10］和赵凤阳［11］运用小波神经网络，对隧道施工的过程中进行了盾构机故障诊断以及沉降建模和沉降预测。曲永玲［12］和周文波等［13］利用多级神经网络，构建盾构法隧道施工中主要施工参数与地面沉降和地面变形之间关系的数学模型。周奇才等［14］结合循环神经网络模型，提出了一种适用于盾构机的故障预测系统。胡珉等［15］提出一种基于BP神经网络的盾构机姿态与轨迹控制参数补偿模型，对盾构机姿态控制参数进行预测和调整，从而使盾构机更好地沿着预定的设计轴线掘进。

基于以上研究，本文在模型控制方法的基础上，通过对比多种常见算法模型，发现神经网络具有更好的数据拟合与泛化能力。因此，结合BP 神经网络的优势，基于两次模型训练方法提出了一种盾构参数预测的神经网络。建立一个盾构机运行参数智能调优算法，可以将盾构机实时运行信息加以整理、分析后快速地提供给盾构控制人员，以达到盾构施工参数最优控制的目的。

1 相关工作

1.1 数据描述

实验数据选自于某市某项目盾构隧道开挖时收集的数据中的某一段。该项目区间隧道最小覆土5.8 m，最大覆土约22.5 m，主要穿过中粗砂、砾砂、圆砾等土层，地下水位较高，部分区间位于河道下方，因此，要求盾构机须适应饱水砂层。该项目所选数据区间土质以圆砾为主，所选盾构机开挖直径为6 280 mm，刀盘转速0～3.7 r/min，最大推进速度80 mm/min，整机总长80 m，装机功率1 689.45 kW。

1.2 正向模型的选取

1.2.1 多项式回归模型

实际应用过程中，自变量和因变量之间存在的相关关系可以用多项式回归模型来求解。但往往自变量之间存在较强的（线性）关系，在一般线性回归中，使用的假设函数是一元一次方程，也就是二维平面上的一条直线。但是，很多时候可能会遇到直线方程无法很好地拟合数据的情况，这个时候可以尝试使用多项式回归。多项式回归中，加入了特征的更高次方（例如平方项或立方项），也相当于增加了模型的自由度，用以捕获数据中非线性的变化。添加高阶项的时候，也增加了模型的复杂度。随着模型复杂度的升高，模型的容量以及拟合数据的能力增加，可以进一步降低训练误差，但导致过拟合的风险也随之增加。

在多项式回归中，最重要的参数是最高次方的次数。设最高次方的次数为k，且只有一个特征时，其多项式回归的方程为

方程可以改写成向量化的形式：

式中：X为大小为m·(k+1)的矩阵；θ为大小为(k+1) ·1的向量。

当使用式（1）去拟合散点时，需要确定两个基本要素，分别为多项式系数θ以及多项式阶数k。

1.2.2 深度神经网络

深度学习作为机器学习的一个重要分支，主要用于对数据进行高层抽象，即利用低层隐藏层提取数据的基本特征，高层隐藏层线性组合上层的特征，从而实现高维特征的提取。通过多个层堆叠构成的神经网络结构即为深度神经网络。节点是构成网络的最小单位，各种运算都在节点之间进行。

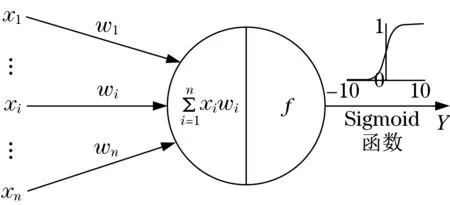
图1 单个节点示意图Fig.1 Schematic diagram of a single node

图1 为单个节点的示意图。节点层类似于神经元的开关，在输入数据通过网络时开启或关闭。从最初接收数据的第一个输入层开始，每一层的输出同时也是下一层的输入。我们将输入特征与可调整的权重匹配，由此指定这些特征的重要性，即它们对网络的输入分类和聚类方式有多大程度的影响。

为了选取最为合适的正向模型算法，首先，用相关性分析优选出对推进速度影响较大的参数；然后，采用多项式回归方法和BP 神经网络方法对这种非线性、不确定的多变量系统进行预测。结果表明，人工神经网络方法具有更好的自适应性，能较好地反映影响盾构机推进过程中的各种微观参数与提高推进决策的内在联系，而且预测精度较高。经过实验对比，认为应用BP 神经网络方法预测盾构机的推进速度是可行和有效的，因此，最终选取BP 神经网络作为正向模型对盾构参数进行预测。

2 反向模型

2.1 输入输出参数

本文结合实际的施工经验和历史数据记录，选取某市特定机型盾构机型号的一段挖掘历史数据，且取出历史数据中较好量化的部分作为特征输入，输入特征为每环一定间隔时间点的记录数据，数据中包含特征如表1所示。

这些值可在一定程度上反映当前盾构机的工作状态和当时操作人员对盾构机的部分参数设定情况。盾构机在穿越管线、铁路和重要建筑物时，为减少土体扰动和土压波动，有效控制地表沉降；盾构机在穿越管线、铁路和重要建筑物时，为减少土体扰动和土压波动，有效控制地表沉降，盾构机的最低推进速度的选取能够起到较好的控制效果。因此，将盾构机的最低推进速度作为模型的输出值。

表1 数据的特征及其对应的单位Tab.1 The characteristics of the data and its corresponding unit

2.2 模型结构设计

在盾构机的实际应用中，工程希望使用观测到的参数调整当前盾构机掘进过程中所设置的重要参数，达到最优掘进效率。基于此想法，本文在正向模型的基础上，提出一种基于深度神经网络的生成模型，该模型在输入层与神经网络层之间新加入了一层权重优化层，通过两次训练后得到最终更新的权重优化层，并将权重优化层的输出作为最终的输出。算法步骤如下：

步骤1随机初始化各层节点的权值，其中，权重优化层的权值矩阵初始化为单位矩阵，在该步骤中梯度不会回流到权重优化层，该层被锁定。

步骤2应用模型的正向传播算法，得到模型的预测值y'，然后与实际值y计算误差函数，通过梯度下降算法得到最优参数。

步骤3将权重优化层参数锁定解除，梯度可以正常传递到该层，其他隐含层权重锁定。

步骤4再次应用正向传播算法，得到的预测值与y(1+Δ)，其中，Δ为人工干预因子计算误差函数，通过梯度下降算法更新参数。

步骤5将权重优化层的预测值，作为最终的输出结果。

反向模型在结构上与正向模型类似，其共用了中间部分多层全连接的权值；不同的是，在输入层前增加权重优化层，其初始权值矩阵为单位矩阵，用I表示；经过神经网络模型计算得到的结果为Y=[y1，y2，…，yi，…，yn]。从输入层神经元i到隐含层神经元j的权值为wij，从隐藏层层神经元j到隐藏层神经元t的权值为vjt。隐含层与输出层均使用Sigmoid 函数作为激活函数，采用梯度下降的方法来进行权值的更新，模型的部分计算公式如下：

第1次训练输入层：

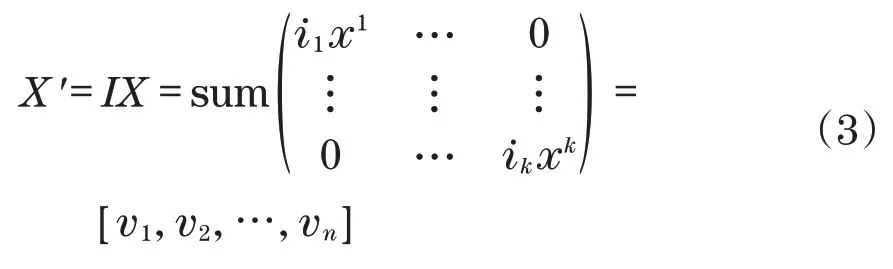
第2次训练输入层：

输出层：

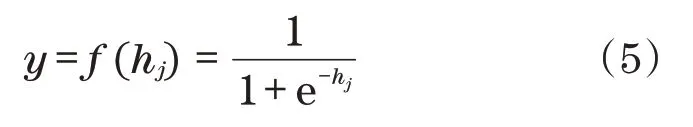
在第一次训练之前，权重优化层需要被初始化为单位矩阵，输入通过权重优化层后不会产生改变。如图2 所示，在第一次训练时，权重优化层将被设置为不可训练，反向传播将更新神经网络层中的参数，使得输入与输出之间达到最优。在第二次训练时，权重优化层将被设为可训练，而神经网络层则被设为不可训练。此时反向传播将更新权重优化层中的参数，而神经网络层的参数则被冻结无法被训练而修改。经过两次训练之后，输入经过权重优化层所得的输出即为最终所需的输出值。

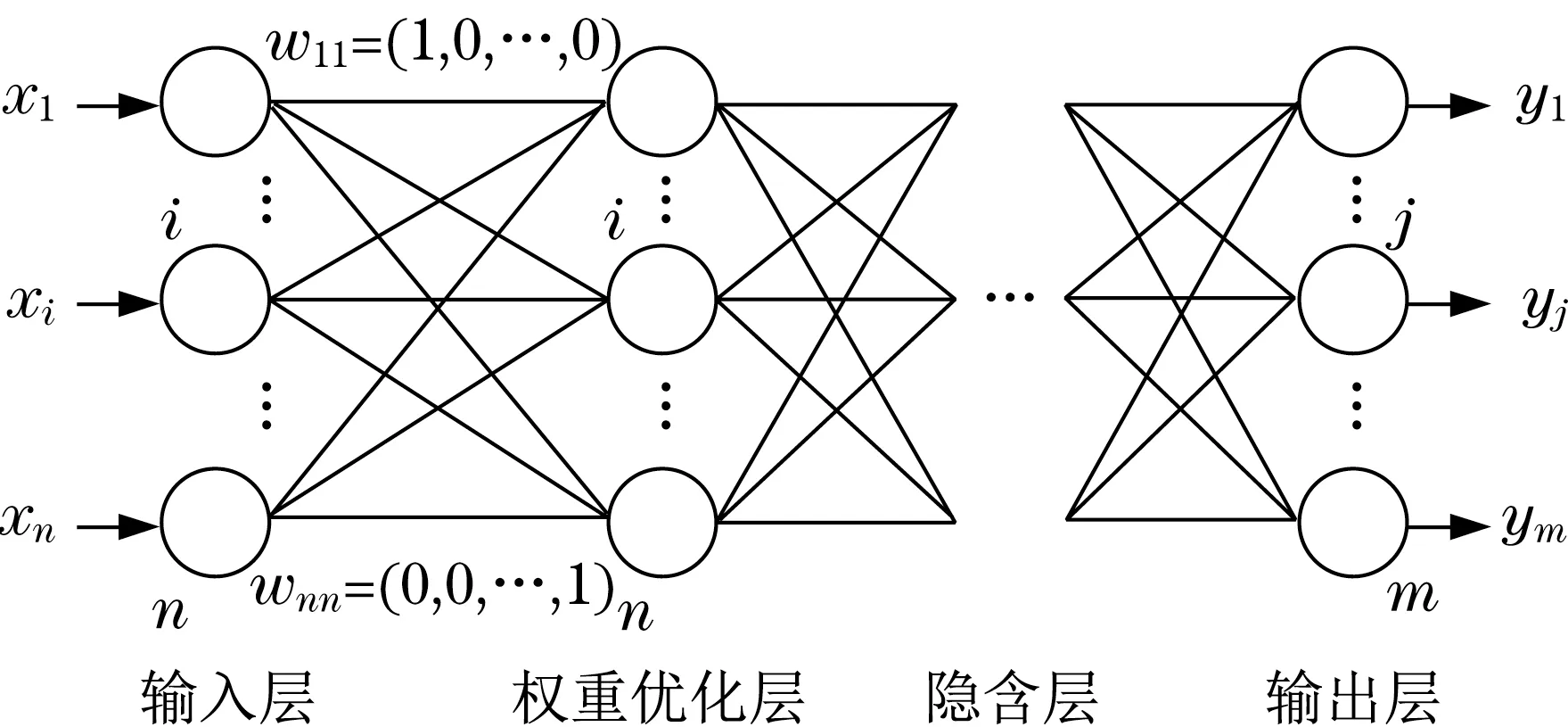
图2 隐含层参数训练Fig.2 Parameter training of hidden layers

3 实验分析

本文一共设计3 组试验，其中，实验一、实验二负责检测正向模型和其他模型对历史速度的拟合程度，拟合程度越高则认为模型效果越好，对于拟合程度利用平均偏离值和平均偏离百分比作为标准。实验三则在实验一的基础上，使用本文提出的反向神经网络模型来预测盾构机掘进参数。

实验一选取了某市某地某区间115～1 807 环之间共计1 693 环的数据作为样本数据进行训练，以后50 环的数据作为预测数据。在对数据进行清洗与预处理之后，以推进速度作为目标值进行预测。训练结果如图3所示。

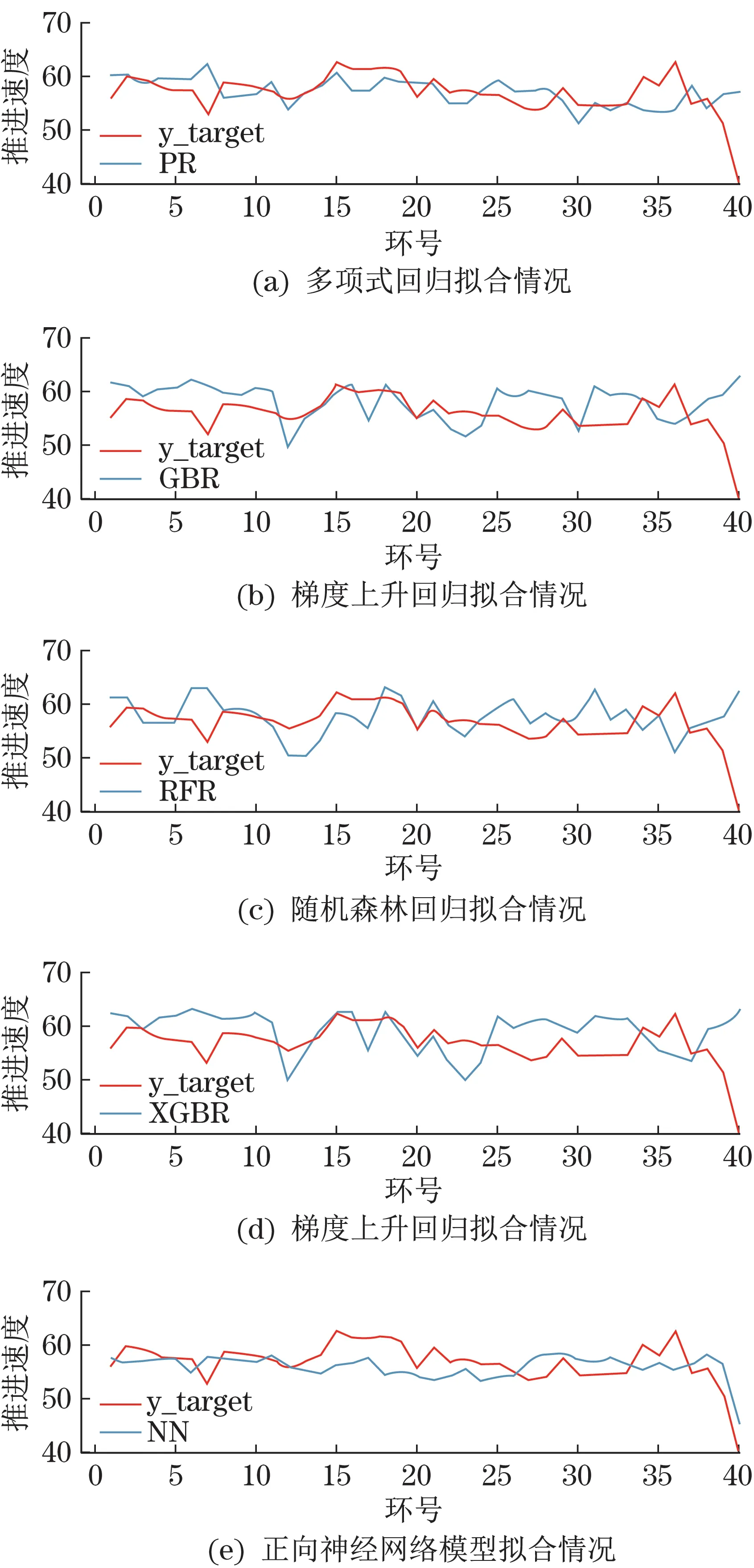
图3 不同模型的训练情况Fig.3 Training of different models

图中可见，正向神经网络模型（NN）相较于多项式回归（Polynomial Regrssion，PR）、随机森林回归（Random Forest Regression，RFR）、梯度上升回归（Gradient Boost Regression，GBR）、极限梯度上升回归（Extreme Boost Gradient Regression，XBGR）能够更好地拟合数据。正向模型输出的波动规律与真实数据相较一致，比较精确地还原出了原始数据的变化情况。我们使用平均偏离值、平均偏离度作为衡量预测值与真实值之间的差异标准，各个模型的误差如表2所示。

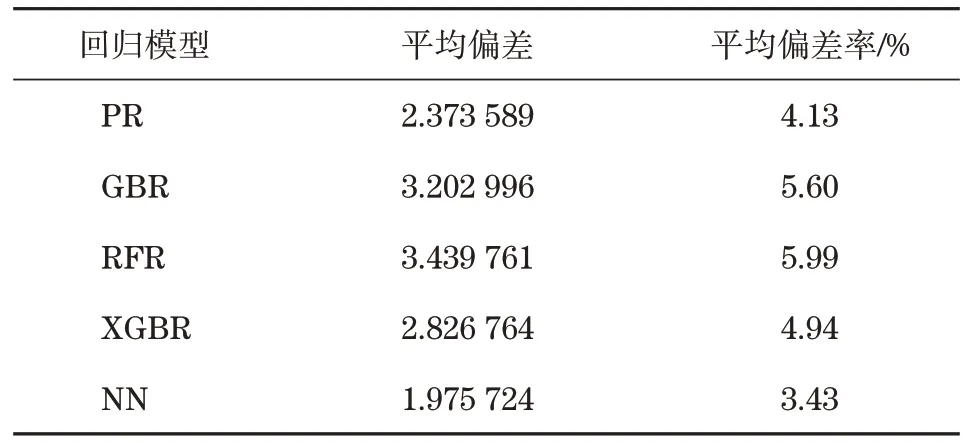
表2 不同模型的误差Tab.2 Error of different models

实验二中选取了某市某地某区间115～1 855环之间共计1 741 环的数据作为样本数据进行训练，以1 856环的数据作为预测数据，各个模型的误差如表3所示。

可以看出，神经网络相较于其他的回归器具有更好的性能，对原始数据具有更好的拟合效果。

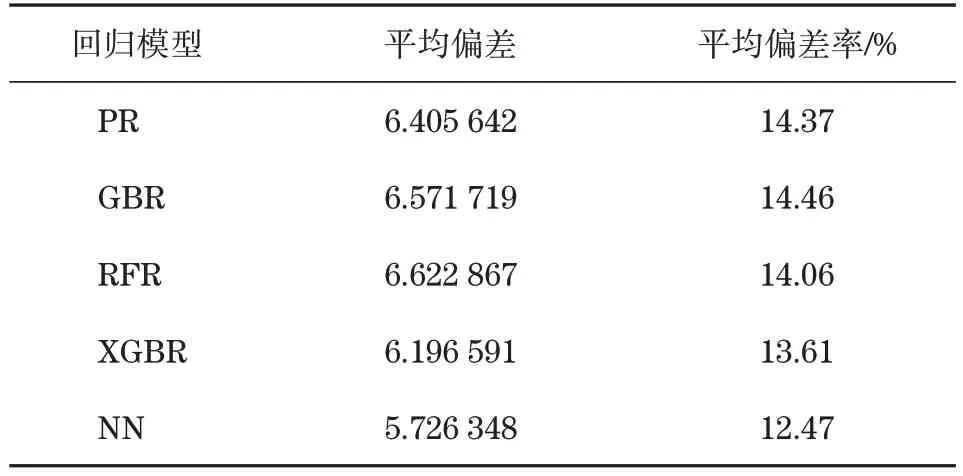
表3 不同模型的训练误差Tab.3 Training error of different models

实验三中，反向模型的训练采用实验一中速度为40～50的样本作为训练数据，速度为48～60的样本作为对照数据。泡沫混合液环累计量以环均数据作为训练样本，最终得到总推进力、刀盘扭矩、推进压力、总功率、刀盘转速、土仓压力、泡沫混合液环累计量的预测值分布与真实值分布，如图4所示。

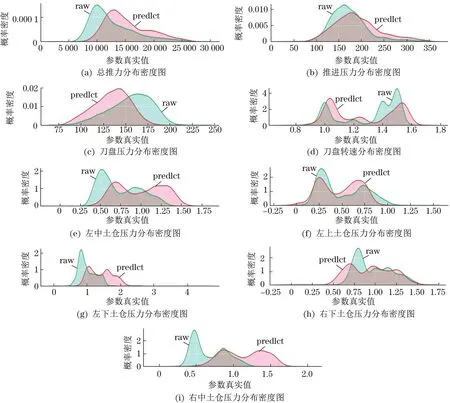
图4 反向模型的训练情况Fig.4 Training of the reverse models

如表4 所示，对比预测数据（predict）与真实的施工数据（raw）可知，预测值与原始施工数据变化规律一致，且预测参数值均在盾构机参数范围内，实际参数与预测参数的区间交并比均值为82.61%。因此，本文提出的反向模型具有轻量级、泛化能力强的特点。

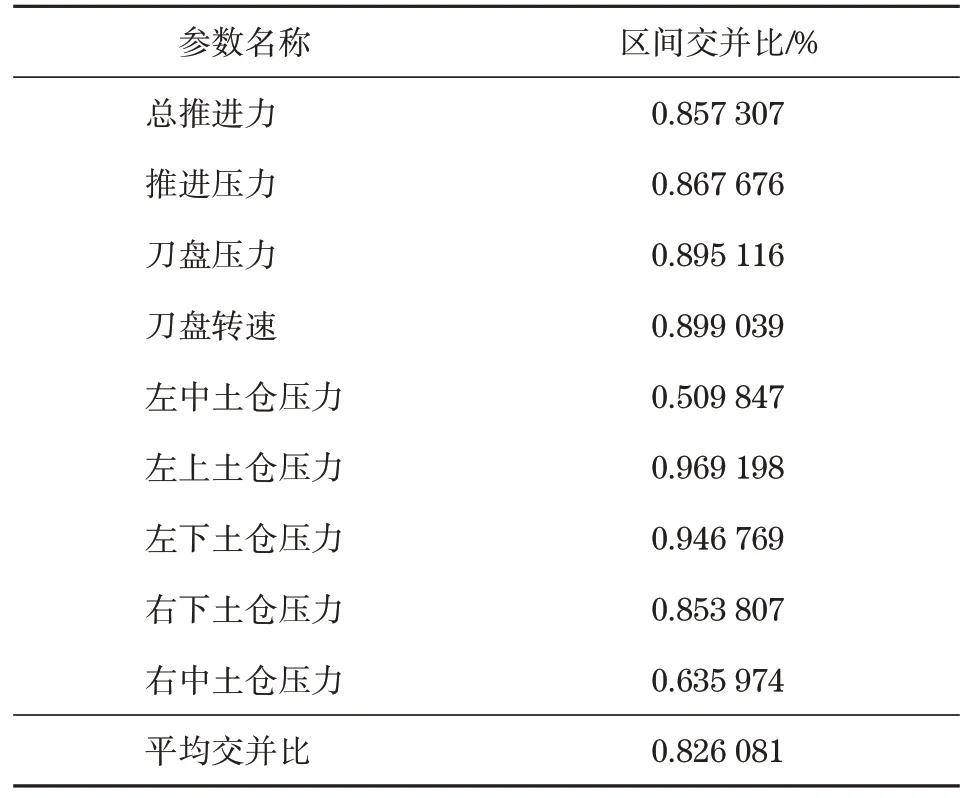
表4 各盾构参数的区间交并比Tab.4 Intervals’intersection over union of shield parameters

4 结语

本文提出的方法可以从大量的盾构机正常施工的数据反向预测盾构机部分掘进参数，实验结果表明，不仅预测结果与真实值的数据变化规律一致、误差小，而且模型具有轻量级、泛化能力强的特点。因此，对盾构机施工有很强的指导意义。传统的盾构机参数设置需要根据相关的公式以及施工经验，而通过本文提出的方法，可以更高效地通过盾构机施工数据反向预测出掘进时设定的参数，并且能反映出施工环境与掘进参数的联系。未来的研究是将不同地质环境下的施工情况都纳入考虑优化神经网络模型，进一步地提高该方法的泛化性，使之在不同的地质环境下也能正确地反向预测出掘进参数，从而辅助施工人员进行决策。