铁路集装箱运输动态服务网络设计及Benders 分解算法*

江雨星 牛惠民 高如虎

（兰州交通大学交通运输学院 兰州730070）

0 引 言

铁路运输正日益成为国际、国内集装箱运输组织的重要形式。作为铁路集装箱运输战术规划层次的重要内容，动态服务网络设计的主要目标不仅是制定列车的开行计划，还需要确定出合理的集装箱分配及中转方案，力求在满足多样化的运输需求、提高客户满意度的同时，尽可能的降低铁路企业的运营成本。可见，铁路集装箱运输动态服务网络的设计与优化具有重要的现实意义。

货物运输服务网络设计问题分为静态服务网络和动态服务网络2 个研究领域，前者是确定运输服务的径路、开行频度及货流的分配，而后者是将前者内容与时间信息结合起来进行优化，从而得到更为详细的运输方案[1]。国内外学者对于货物运输服务网络设计问题作了大量研究，其中，铁路货物运输的相关文献一直占据相当大的比重。Duan等[2]考虑了铁路货物运输的时效性及可靠性，通过构建线性整数规划模型和设计启发式算法，实现货物在列车服务中的分配。Lulli 等[3]以意大利铁路货物运输为背景，研究了服务网络的设计方法。王保华等[4]研究了考虑车辆周转的铁路货物运输动态服务网络设计问题。沈睿[5]针对行包专列静态服务网络和客运普包动态服务网络设计问题，分别构建了整数规划模型。唐金金等[6]以车流总旅行费用最小为目标，构建了服务网络动态配流的优化模型。

对于时效性要求较高的铁路集装箱运输，既有研究主要为静态服务网络设计。夏阳等[7]针对客运化模式下的铁路集装箱运输系统，建立了班列开行方案的优化模型，并设计模拟退火算法进行求解。张小强等[8]对铁路集装箱班列开行决策与运输价格制定的协同优化进行了研究。闫伟等[9]通过构建数学优化模型解决了铁路集装箱运输组织模式选择及班列开行方案制定的问题。

从既有研究中可知，运输服务网络设计通常是1个大规模的线性优化问题，涉及众多决策变量及约束条件，如何设计有效的求解算法，同样是许多学者关注的问题。启发式算法是常采用的方法，如模拟退火算法[2]、遗传算法[10-11]等，虽然这些方法可在接受的时间内给出优化问题的1 个可行解，但是无法评判该可行解与最优解的偏离程度。为此，部分学者运用了分解思想，将大规模的复杂问题分解为若干规模较小的子问题，如列生成算法[12]、拉格朗日算法[13-14]等。针对于大规模线性混合整数规划，部分学者运用了Benders 分解算法，将原问题按变量类型分解为相对易于求解的主问题与子问题，通过反复迭代得到原问题的最优解。该方法已多次用于解决网络设计的相关优化问题，例如Fontain等[15]运用Benders 分解算法解决了危险货物运输的网络设计问题，Gelareh 等[16]运用该算法求解了班轮运输服务网络设计的优化模型。但是，Benders分解算法存在一般迭代算法的缺点，如迭代次数多、收敛较慢等。为克服这些问题，部分文献中对该算法进行了改进。何必胜[17]在每一次迭代中，运用智能算法获取大量的可行解,并以此得到多个割平面，减少主问题的解空间。Naoum 等[18]和Fortz 等[19]针对于一类特定问题中对偶子问题存在多个最优解会产生不同割平面的情况，运用Pareto 最优割平面的理论对算法进行了改进。

综上，对于铁路货物运输动态服务网络设计问题，现有研究已取得丰富成果。由于该问题涉及众多因素及约束条件，求解难度大，既有文献在研究时，对问题进行了简化，优化时没有考虑货物中转方案与动态服务网络设计的同时优化, 是在给定货物中转方案的基础上,考虑如何设计服务网络。而货物中转方案是铁路货物运输决策的核心，与列车开行计划的制定紧密联系。基于这一现状，笔者依据集装箱的流量及流向（下文简称为箱流），充分考虑箱流的中转方案，构建铁路集装箱运输动态服务网络设计的线性规划模型，运用Benders分解方法将原问题分解为仅包含0-1 变量的网络设计主问题及固定0-1变量后的箱流分配子问题，并在主问题模型中添加有效不等式，使主问题更加紧致，以加快算法的收敛速度。

1 问题描述

目前，我国铁路运输部门组织开行的集装箱班列主要为直达班列，即班列在途经站不办理任何集装箱装卸和车组甩挂作业。基于此，本次研究中假定任意2个集装箱办理站（以下简称为办理站）间开行的集装箱班列均为直达班列。结合动态服务网络构建的思想，先将设计周期划分为一定数量的单位时段，再将铁路物理网络中的办理站点按照周期及各个时段拆分为若干节点，此时每个节点即代表所在办理站，又代表所处时段。为能反应箱流在途经站的中转作业过程，进一步将每个节点拆分为接入节点和出发节点。在此过程中，需要注意单位时段的取值，参照客运普包动态服务网络设计中单位时段的确定方法[5]，令箱流的中转作业时间为单位时段。见图1，已知设有4 个办理站的铁路线路，研究周期为24 h，箱流中转作业时长为3 h，则单位时段为3 h。构建的动态服务网络见图2。节点间的有向弧段分为3 类：①弧段的起终节点所在办理站相同，且同为接入节点或同为出发节点，所处时段为相邻的2 个时段，这类有向弧段为延迟弧段，代表集装箱在办理站的等待过程，见图2中的延迟弧段1；②弧段的起终节点所在办理站相同，但时段不同，且起点为接入节点，终点为出发节点，这类有向弧段为中转弧段，代表集装箱在办理站的中转作业过程，见图2中的中转弧段1；③弧段的起终节点所处时段不同，且起点为某一办理站的出发节点，终点为另一办理站的接入节点，这类有向弧段为班列弧段，代表办理站之间提供的每一趟班列服务，见图2 中的班列弧段1。参考集装箱班列开行方案的编制[7]，本文中班列服务开行与否的决策采用基于备选集的方法，备选集是研究周期内可提供运输服务的所有班列弧段的1个集合。

图1 铁路物理网络图Fig.1 Railway physical network

图2 动态服务网络Fig.2 Dynamic service network

铁路集装箱运输动态服务网络的设计，就是在弧段集合中选出一系列连续的弧段组成服务路径来运输节点间的集装箱。对于任意2 个节点间的箱流，可能有多条服务路径供其选择，不同的服务路径代表着不同的运输方案。若箱流中转方案改变，选择的服务路径会随之改变。例如：已知箱流1，其出发站为B，目的站为D，产生时段为第3时段，运到期限为5 个时段，该箱流在动态服务网络中的出发及目的节点见图2 中虚线圆圈标记，其中目的节点是通过出发节点所处时段加上运到期限来确定。若B站至D 站的箱流选择直达运输，则箱流1 可由延迟弧段1、延迟弧段2 和班列弧段3 组成的服务路径来运输，该方案表示箱流1 在B 站停留至第5 时段，由该站在第5 时段组织开往D 站的班列进行直达运输；若B站至D站的箱流在C站中转，且中转后由C站发往D 站的班列承运，则箱流1 可由班列弧段1、中转弧段1和班列弧段2组成的服务路径运输，该方案表示箱流1 由B 站在第3 时段发往C 站的班列承运，到达C 站后卸下，再装至C 站在第6 时段发往D站的班列将其运至目的节点，其中在C 站的中转作业消耗了1个时段。可见，中转方案的考虑，使得箱流与弧段的对应关系变得更为复杂，从而极大的增加了动态服务网络设计的难度。在优化过程中，假设办理站作业能力始终满足运输需求，既不考虑延迟弧段和中转弧段的能力限制。

2 优化模型构建

2.1 参变量定义

2.2 优化模型

2.2.1 目标函数

本文以总成本最小为优化目标，总成本分为2个部分,一部分是班列的开行成本,另一部分是与集装箱运输有关的成本，后者又包括途中运输成本、延迟成本及中转作业成本，则目标函数见式（1）。

2.2.2 约束条件

1）流量守恒约束。动态服务网络中所有节点上进、出箱流量必须满足守恒约束,不得出现箱流的缺失或增加，并保证箱流能够从出发节点运至目的节点。

为了保障送达速度,通常会要求办理站l 至办理站k 的集装箱在途经站的中转次数不能超过规定的最大次数ml，k。

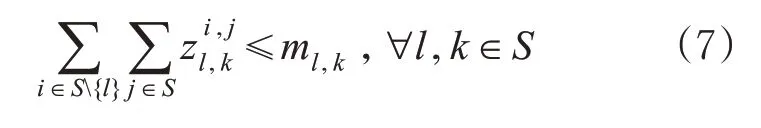
3 算法设计

3.1 子问题对偶模型

3.2 主问题模型

3.3 Benders分解算法流程

3.4 Benders分解算法改进

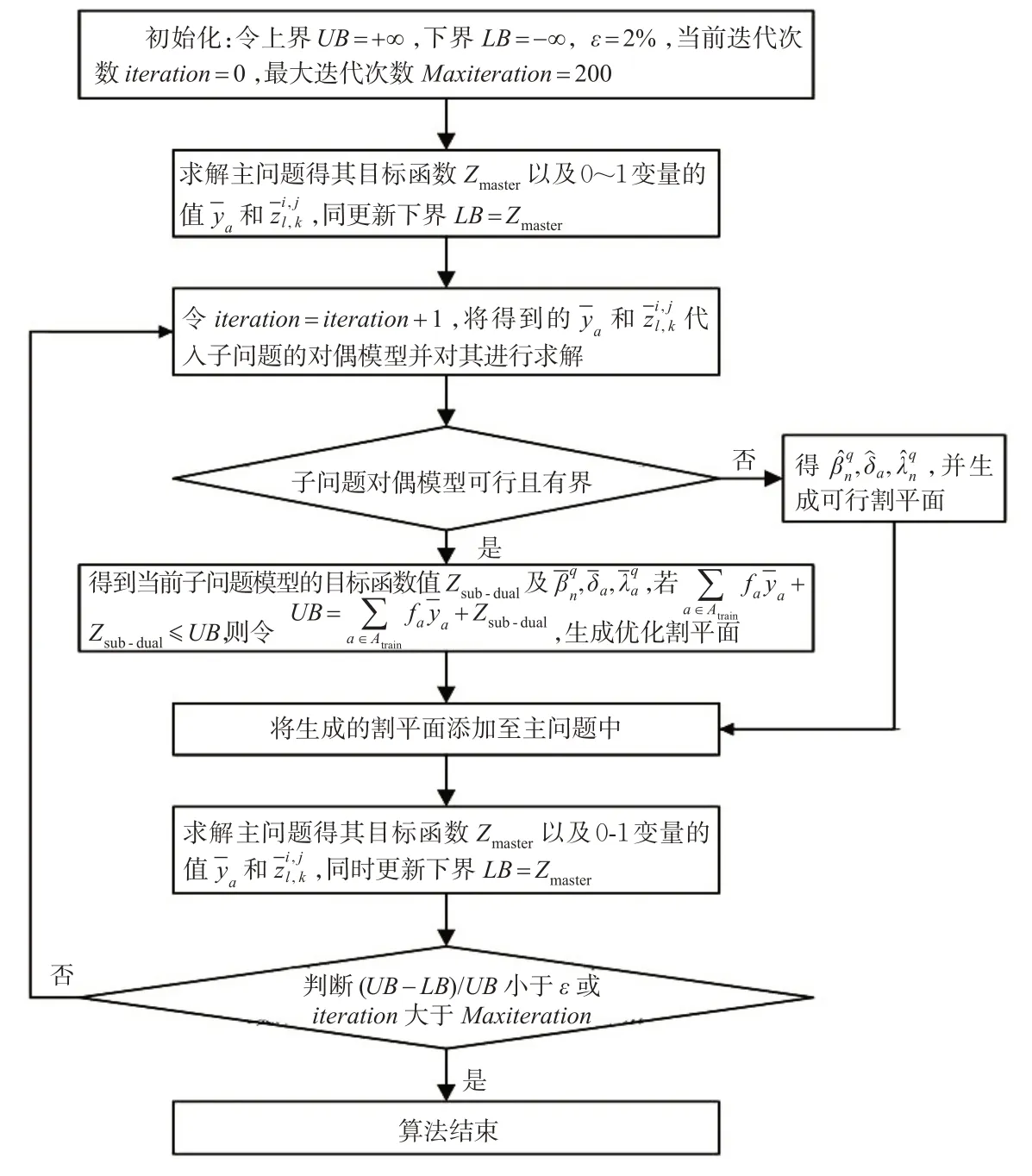
图3 Benders分解算法流程图Fig.3 Flow for Benders decomposition

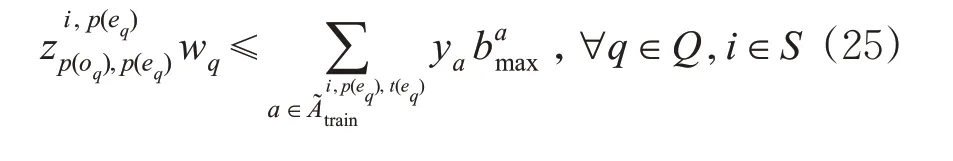
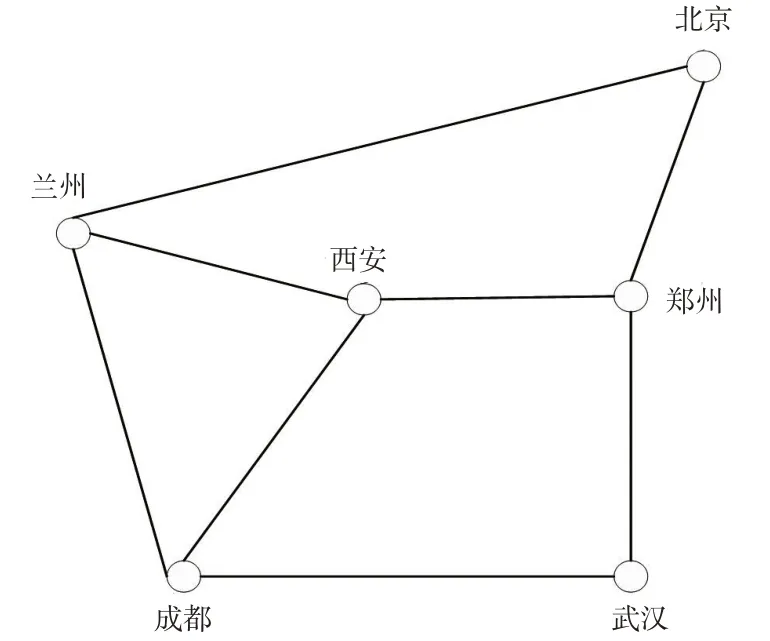
图4 铁路物理网络图Fig.4 Railway physical network

4 求解算例

4.1 参数输入

选取北京、郑州、西安、武汉、成都和兰州这6 个铁路集装箱办理站构建集装箱运输网络，见图4。图中圆圈表示集装箱办理站，连线为办理站之间的路段。决策周期为24 h，考虑到箱流在办理站上的中转作业时间为3 h，则构建动态服务网络时单位时段的取值为3 h。单个集装箱的中转作业成本为20 元/箱，延迟成本为10 元/箱。班列的最大编成箱数为50 箱。班列服务相关参数见表1，箱流信息见表2。

表1 班列服务相关参数Tab.1 Related parameters of train service

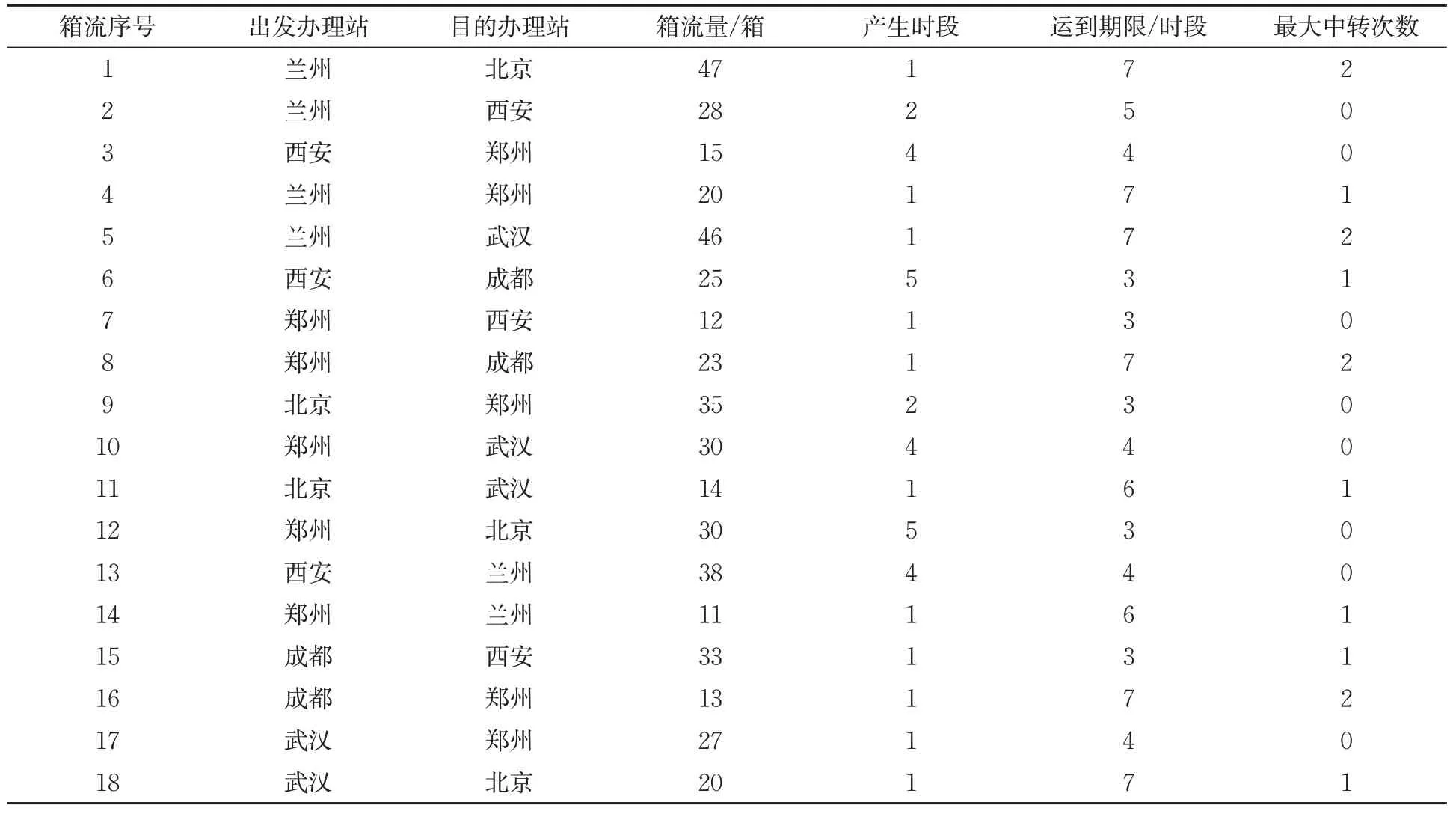
表2 箱流信息Tab.2 Information of container flows

4.2 数值结果

4.2.1 结果分析

算法由Python 语言实现，运行环境为1 台CPU Intel，4GB内存的个人计算机，算法中的主问题与子问题均通过GUROBI 进行求解。主问题的初始解为所有箱流均采用直达运输模式的服务网络，相应的集装箱班列开行方案见表3，代入子问题模型求解得到该方案的总成本为552 480元。在经过69次迭代，运行46 s 后得到最终解，总成本为439 490 元，最终的Gap为1.56%。为分析算法性能，运用未改进的Benders 分解对该算例进行求解。在运行了相同的时间46 s 后，得到目标函数值为450 490 元，Gap为45.17%。可见，提出的改进策略有效提高了算法的求解效率。

表3 直达运输模式的集装箱班列开行方案Tab.3 Service plan of direct transportation organization

表4 集装箱班列开行方案Tab.4 Service plan of container trains

优化结果中班列的开行方案见表4，箱流的中转方案见表5。由表4 数据可知，有12 条班列弧段被选择作为服务网络的组成部分，即在设计周期内共开行12 列集装箱班列，各班列的编成箱数接近于最大编成箱数50 箱，运输能力被充分的利用。表5中，部分箱流在途中不进行任何装卸中转作业，从出发办理站直达运输至目的办理站，如兰州运往北京的箱流（箱流1）；而流量较小且运距较远的部分箱流要在途中进行装卸中转作业，如兰州运往郑州的箱流（箱流4），先由兰州办理站在第2 时段发往西安办理站的班列承运，到达西安办理站后卸下，再装至西安办理站在第6 时段发往郑州办理站的班列将其运至目的站，在西安办理站的中转作业消耗1个时段。

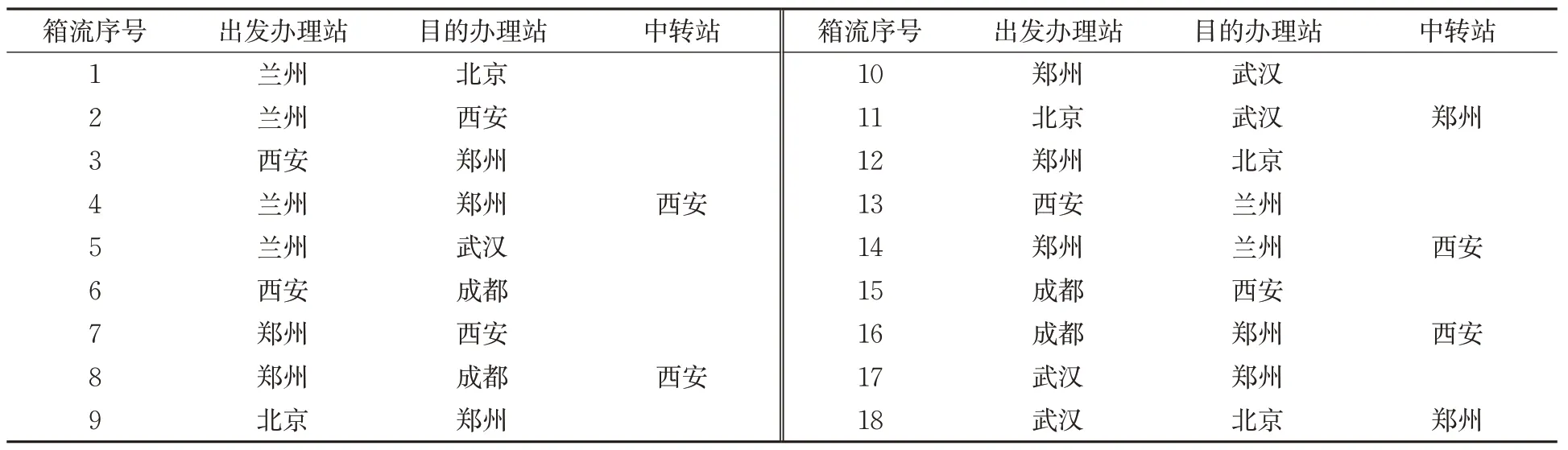
表5 箱流中转方案Tab.5 Transfer plan of container flows

4.2.2 对比分析

比较表3与表4方案的总成本，不难看出优化后的服务网络（表4 方案）节省了20%。同时，将该优化方案与现有集装箱班列开行方案进行对比分析，从“95306”和“中铁集装箱运输有限公司”网站公布的数据汇总得出现有集装箱班列开行方案见表6。通过对比可看出，优化方案中各线路中班列的开行频率为1列/d，而现有班列开行方案中，开行频率普遍在0.5 列/d，无法保证箱流的运到期限。例如现有开行方案中，郑州至成都的箱流（箱流8）是由郑州开往成都的集装箱班列进行承运，每日该去向的箱流量仅产生23 箱，为达到满轴或满长的发车条件，通常每2 d 发1 列车，导致出发站当日产生的集装箱在第2 d 甚至是第3 d 才能被送至目的站，超过了要求的运到期限（7个时段）。优化后的服务网络（表4 方案）中，箱流8 先同箱流7、箱流14 合并，由郑州办理站在第1 时段发往西安办理站的班列承运，到达西安办理站后卸下，再同箱流6 合并，装至西安办理站在第5 时段发往成都办理站的班列，整个运输时间为6 个时段，满足了该组箱流运到期限的要求。显然，利用本文模型及算法得到集装箱班列的发车时段、开行频率在满足运输需求的同时，保证各组箱流在规定的运到期限内送至目的站。

表6 现有集装箱班列开行方案Tab.6 Existing service plan of container trains

5 结束语

本文研究了铁路集装箱运输动态服务网络的设计方法，运用Benders分解算法求解构建的线性混合整数规划模型。通过算例的求解表明：对于大规模的动态服务网络设计问题，改进的Benders分解算法可在较短时间内得到高质量的解；利用本文模型和算法得到的动态服务网络可有效减少铁路运输企业的成本，并在满足运输需求的同时，保证各组箱流在规定的运到期限内送至目的站。在铁路集装箱运输组织中，部分班列需在途经站办理一定的集装箱装卸或车组甩挂作业，今后的研究会针对这一情况做深入分析，以扩展问题的适用性。