巡航速度控制下航空公司受扰航班一体化恢复

杨新湦， 屈琮博， 王梓旭

(1.中国民航大学中欧航空工程师学院， 天津 300300； 2.中国民航大学空中交通管理学院， 天津 300300)

航空运输系统是一个复杂的巨系统，航班不正常是每个航空公司不可避免会面临的问题。航空公司大面积不正常航班恢复是困难问题，一般而言，航空公司不正常航班恢复可分为分阶段恢复与一体化恢复。分阶段恢是将整个恢复问题分为飞机恢复、机组恢复、旅客恢复三个阶段逐步求解；一体化恢复则是综合考虑飞机、机组、旅客因素。

对不正常航班恢复的研究多数集中于分阶段恢复研究。Teodorovic等[1-4]在1984～1995年先后对飞机停运、机场关闭航班恢复问题、旅客恢复和机组恢复问题进行了研究。分别使用分支定界、动态规划、启发式算法进行了求解，奠定了不正常航班分阶段恢复的基础。吴刚等[5]提出一种改进列生成算法，每次迭代过程中加入多个列，并对加入的多个列需要满足的条件进行了分析，最后给出的算例验证了该方法的正确性和有效性。田倩南等[6]改进时空网络算法，给出占优准则，有效减少了可恢复航线的组合数量，提升计算效率。

已有文献中多采用时空网络进行建模，时空网络中不仅有描述航班衔接的航班边，还有机场节点和时间节点。当进行一体化建模时导致模型过于复杂。Sherali等[12]系统介绍了航班网络的使用，相比时空网络模型复杂度低，但是不能将时间、地点等属性表现在图中，诸如飞机维修约束、机组执勤时间约束、客票取消操作不易表达。对于巡航速度控制的策略，Aktürk等[13]在飞机恢复问题中首次使用，并分析了巡航速度控制的优势，Arkan等[14]基于此研究进一步将旅客行程加入模型，但是都没有达到真正的一体化恢复。

基于以上文献中的不足，现做出如下工作：①改进航班网络的弊端，并设计一种基于广度优先搜索的网络生成算法；②建立巡航速度控制下的一体化恢复模型；③使用双曲不等式修正模型，符合二阶锥规划条件后进行求解并通过算例说明巡航速度控制在一体化恢复中的作用。

1 航班网络改进与算法设计

1.1 航班网络改进

针对航班网络相较于时空网络不能表达出飞机维修、调机、客票取消、加机组等操作的劣势进行改进。传统航班网络如图1所示，其中包括三类节点和三类弧，改进航班网络中有四类节点和五类弧，新加入必经节点和必经弧、添加弧，具体如下。

sr为初始节点；tr为沉没节点；Mr为必经节点集合；f、g为航班

源节点：表示飞机、机组或旅客初始状态的点，有时间、地点属性。地点属性是飞机、机组、旅客行程的首发机场，时间属性是首发时间。

末节点：表示飞机、机组或旅客的终止状态的点，有时间、地点属性。地点属性是对飞机停场过夜机场的限制，时间属性是过夜机场的宵禁时间。

航班节点：表示飞机、机组执行的航班或旅客在其行程中要乘坐的航班。

必经节点：表示飞机在特定时段在特定机场维修的节点，或机组规定在特定机场休息。

出发弧：连接源节点与航班节点的弧，表示飞机、机组、旅客执行首个航班。

沉没弧：连接航班节点与末节点的弧，表示飞机、机组、旅客执行完最后一个航班。

航班弧：航班节点之间的弧，表示飞机、机组、旅客执行完上游航班后执行下游航班。

必经弧：连接航班节点与必经节点之间的弧，表示飞机维修、机组休息等。

添加弧：表示航班恢复的特殊操作，如加机组、调机操作(航班节点之间、源节点与末节点之间、源节点与航班节点、航班节点与末节点之间)；乘客客票取消操作(源节点与末节点之间、航班节点与末节点之间)。

1.2 航班网络生成算法设计

一体化恢复包含飞机、机组、旅客三种子网络，用r表示。算法设计中，F为航班集合；closetimedown为机场开始关闭时间；closetimeup为结束关闭时间；curfew为机场宵禁时间；Ntemp为航班暂时存储器中符合条件的航班f集合；Nnext为航班暂时存储器中符合条件的航班g集合；Orig为航班g的始发地，Desf为航班f的目的地；ctfg为航班衔接时间；Nr为节点集合；Vr为弧集合；Er为添加弧集合。航班网络生成算法由Generatesubnetwork(r)，Generatepath(Ntemp)和Insert(Ntemp) 三部分组成。具体步骤如下：

Step1 初始化节点集合Nr，弧集合Vr，Ntemp=sr。

Step2 Generatesubnetwork(r)，航班网络生成主程序如下。

Procedure Generatesubnetwork(r)

Gr=(Nr,Vr)←Generatepath(Ntemp) #为第二部分程序

Vr=Vr∪Er

Return Gr=(Nr,Vr)

end Procedure

Step3 Generatepath(Ntemp)，基于广度优先搜索可衔接航班，即航班网络路径中的节点。

Procedure Generatepath(Ntemp)

WhileNtemp≠∅

f←first element ofNtemp

ifclosetimedown≤[dtf,atf]≤closetimeuporatf≤curfew

Updatedtfandatf#修改航班的OD时间

ifdtf-sdtf> 最长延误时间

continue

else

Nnext←(g∈FOrig=Desfandsdtg≥atf+ctfg)

#当前航班的可衔接航班

for eachginNnext

Ntemp=Ntemp∪{g}

ifg∈Nr

Insert(Ntemp) #第三部分节点/弧生成程序

else

if Desf=Desr

end if

end if

end for

end if

end if

end procedure

Step4 Insert(Ntemp)，得到航班网络中的所有弧与节点。

Procedure Insert(Ntemp)

以实施“美丽乡村小康水”行动计划为主抓手，贵州省全面推进民生水利建设，让更多群众在水利发展中得到实惠。2013年全省预计解决300万农村人口及学校师生的饮水安全问题，实施中小河流项目129个，治理水土流失面积2 200km2，实施病险水库治理271座，新增小水电装机20万kW，新增小型农田水利重点县22个，新增有效灌溉面积73万亩，全面完成年初预定的各项目标。

Nr=Nr∪Ntemp∪Mr

fori=1:len(Ntemp)

Vr=Vr∪{fi,fi+1}

end for

end procedure

Step5 对Vr进行分类得到出发弧、沉没弧、航班弧、必经弧、添加弧；对Nr进行分类得到初始节点、航班节点、沉没节点。

Step6 如果是机组子网络，额外删除不满足机组执勤时间和飞行时间的弧与节点。

2 巡航速度控制与一体化恢复模型

2.1 巡航速度与燃油消耗

飞机在最大航程速度(maximum ragne cruise，MRC)下最省油，在巡航速度大于MRC速度时燃油消耗随速度增加而增加。速度控制综合考虑加速与减速研究速度控制对航班恢复的影响，减速考虑飞机的反常操作，按照文献[15-16]的建议巡航速度调整范围在MRC速度的[-10%,+10%]。将巡航速度纳入模型需要速度与燃油消耗之间的关系以计算恢复成本，欧洲交通管理组织的飞机数据基础(base of aircraft data, BADA)项目中开发的巡航阶段燃料流模型，提出给定质量和高度，可以计算出飞机巡航阶段的燃油消耗率fcr(v)(kg / min)与速度v(km / min)的关系[17]为

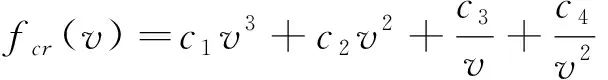
(1)

式(1)中：c1、c2、c3、c4分别为与飞机阻力、油耗系数、给定高度的空气密度和重力加速度相关的系数，这些系数可以从399种飞机的BADA用户手册中获得。给定燃油消耗率可以计算出巡航阶段总燃油消耗，假设飞行距离固定为d，那么可以得到巡航总耗油为

(2)

飞机以MRC巡航最省油，但是实际运行中MRC速度接近反常操纵区，常采用经济巡航或LRC巡航，假设航班的计划飞行速度都为经济巡航速度vECON(按照MRC巡航速度的1.02倍计算)，那么巡航速度调整后，航班燃油成本ΔFuelcost变化为

ΔFuelcost=pfuel[F(v)-F(vECON)]

(3)

式(3)中：pfuel为单位燃油价格；F(vECON)为经济巡航速度下总耗油。

2.2 巡航速度与碳排放

飞机巡航阶段不仅是飞行时间、燃油消耗最多的阶段，也是污染物排放最多的阶段。国际民航组织(International Civil Aviation Organization，ICAO)根据发动机厂家审定的数据，定义了标准起飞着陆循环(land take-off，LTO)，包括起飞、滑行、爬升、着陆4个阶段[18]，在基础排放模型中给出4个阶段的基础排放数据见表1。Tamara使用ICAO数据结合波音公司的BM2方法对英国一天的流量样本的燃油消耗与二氧化碳排放进行了分析，并与英国最广泛使用的NETCEN估算进行了对比，确定了其实用性[19]。从表1可以看出，CO2的排放指数与飞行阶段无关，魏志强等[20]研究指出CO2的排放量与燃油消耗成正比，占飞机排放物总量的99%以上，同时也是节能减排关注的重点。巡航速度的改变使燃油消耗变化导致二氧化碳排放的因素在模型中也将予以考虑，二氧化碳排放量Δcarboncost可以按照式(4)计算。

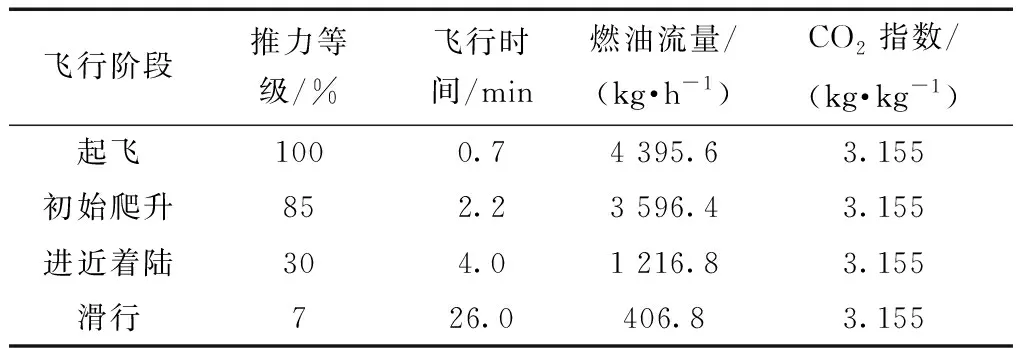
表1 CFM56-7B26 发动机基准排放数据[18]

Δcarboncost=pCO2k[F(v)-F(vECON)]

(4)

式(4)中：pCO2为单位燃油二氧化碳排放量；k为二氧化碳指数。

2.3 一体化恢复模型

在模型提出之前做如下假设。

(1)飞机除座位数之外的性能差异不大，即不同飞机对巡航速度调整的限制相同，航班被不同飞机执行若没有速度调整其计划巡航时间保持不变。

(2)飞机的计划巡航速度设为MRC的1.02倍，且不考虑航线上风和温度变化的影响，速度调整范围在[-10%，+10%]。

(3)对于多段行程的旅客不能使其到达中间地点后无后续航班，在恢复期内对旅客行程受到扰动的旅客进行转到其他航班调整，不受扰动的航班上的旅客不可调整后受扰。

(4)飞行中的非巡航部分如滑行、起飞、爬升、下降的总时间为40 min。

模型算法中的集合参数变量定义如下：

集合

ac飞机集合MidN中间节点集合

cr机组集合MN必经节点集合

ps旅客行程集合arcs弧集合

Rr∈ac，cr，pssrarcs出发弧集合

N节点集合trarcs沉没弧集合

SN首节点sr集合midarcs中间弧集合

TN末节点tr集合cntarcs联程航班弧集合

F航班集合psnumber安排到航班的人数之和

参数

atf航班f计划到达时间tf航班f飞行时间

DTf航班f实际起飞时间Np行程p的旅客人数

ATf航班f实际到达时间Nf原航班上旅客人数

df航班f的巡航飞行距离S飞机可用座位数

ctfg中转衔接时间etr飞机或机组的最早可用时间

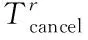
客客票取消成本

Cfd航班f取消成本CCO2碳排放成本

δtf航班f巡航缩短时间Cfuel燃油成本

Cps旅客单位延误成本

变量

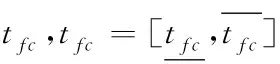
对于每种网络要满足网络的流平衡约束和节点闭合约束。流平衡约束指每个网络的源节点到中间节点的弧有且只有一个，每个网络的中间节点到沉默节点的弧有且只有一个，中间节点的进入弧与出发弧数量相等。节点闭合约束指若弧fg被执行则ac与cr中的弧fg必有且只有一个被执行。如约束(5)～约束(10)。约束(5)～约束(7)是经典图论模型的基本约束，约束(8)表示若弧fg被经过则飞机、机组网络中必同时有弧fg被执行，约束(9)与约束(10)表示航班f只能被一架飞机和一个机组执行，由于旅客行程可以将旅客分配到任一或多个OD相同的航班因此无此约束。

(5)

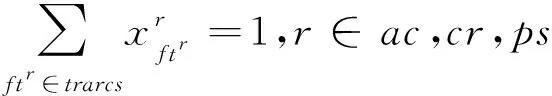
(6)

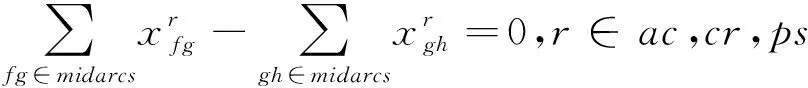
(7)

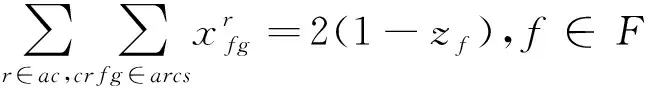
(8)

(9)

(10)

对于不同的飞机有飞机特性约束，如飞机座位数约束，旅客行程被安排到航班f时的人数之和不能大于执行这个航班飞机的座位数如约束(11)。被分配旅客行程的人数与旅客行程取消人数之和等于原旅客行程人数如约束(12)。不同的飞机对于速度的调整限度相同，但是由于各飞机的MRC速度不一样因此巡航时间调整并不相同，不同航线上的速度调整限制不同，如约束(13)。约束(14)表示机组仅可以执行执照允许的飞机任务，ac(cr)表示可以执行飞机ac的机组集合，约束(15)表示飞机不可以执行规定之外的航线(如高原航线由特定飞机执飞)，ac(f)表示飞机ac可以执行的航线集合。

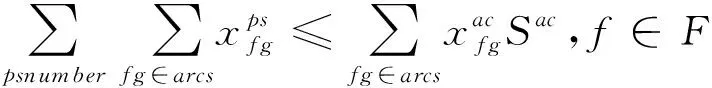
(11)

(12)

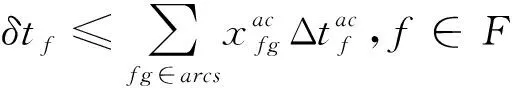
(13)

(14)

(15)

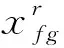
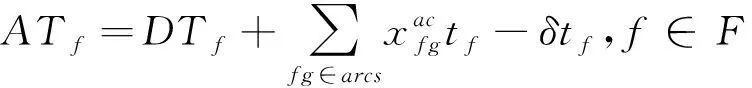
(16)

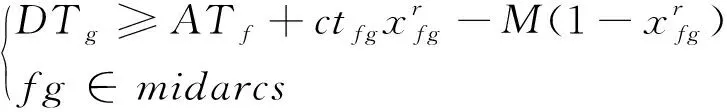
(17)

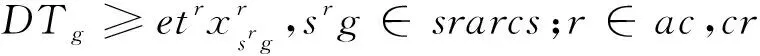
(18)

0≤DTf-dtf≤480

tfd=ATf-atf,f∈F

(19)

0≤atf≤curfewf,f∈F

(20)

根据第2.1节的阐述，将速度变化带来的燃油消耗变化纳入约束中，为了减少模型中的变量将速度用距离除以巡航时间表示，系数c1、c2、c3、c4也相应改变，如约束(21)～约束(24)，其中Tfc是计划巡航时间，当不考虑巡航速度时，则没有约束(21)～约束(24)。

(21)

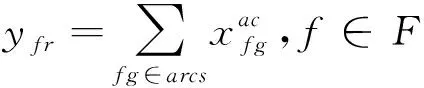
(22)

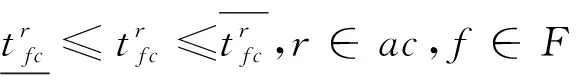
(23)

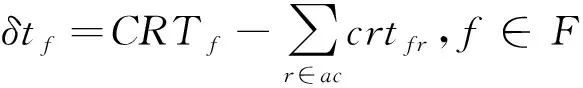
(24)

模型的目标函数以最小化成本表示，成本分为航空公司延误运营成本(Cop，包括航班运营延误成本与机组空闲成本)、航班取消成本(Cfd)、旅客延误成本(Cpd)、客票取消成本(Cpc)、速度变化带来的额外燃油(Cfuel)与碳排放(Cco2)成本。民航局在《航班延误经济补偿指导意见》中的赔偿建议，延误8 h以上给出的赔偿标准已经接近于取消航班的赔偿，所以我们认为航班取消成本是航班延误8 h的运营成本；旅客客票取消成本是旅客延误8 h经济损失加上客票价格。

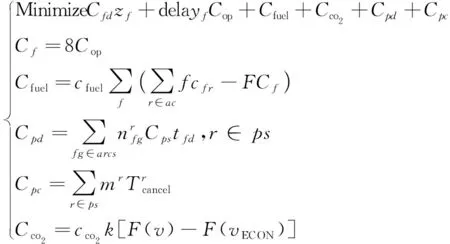
(25)

3 基于二阶锥优化的模型求解

二阶锥规划(second-order cone programming，SOCP)可以视作线性规划的推广, 本质上是一种凸规划, 解的最优性和计算高效性都有优良特性。利用现有的CPLEX等算法包可以获得较好的求解结果, 诸多基于SOCP的优化问题可以在多项式时间内完成。本节用到相关定义如下。

(2)上镜图：函数f：Rn→R的图像定义为{[x,f(x)]|x∈domf},它是Rn+1空间上的一个子集，则epif={(x,t)|x∈domf，f(x)≤t}是该函数上镜图[21]。还有定理，函数f是凸函数当且仅当epif是凸集。

(3)双曲不等式：如u2≤v1v2，易证明双曲不等式可写成二阶锥不等式‖(2u,v1-v2)‖≤v1+v2。

一体化恢复模型中约束(21)是非线性约束，是非线性不连续的，因此其上镜图是非凸的，约束非凸，模型中的目标函数与其他约束条件也受约束(21)的影响。为了简化说明删除了变量索引，约束(21)的上镜图可表示为

t≥df(c1λ1+c2λ2+c3λ3+c4λ4)

(26)

y4≤λ1t2y

(27)

y2≤λ2t

(28)

t2≤λ3y

(29)

t4≤λ4y2t

(30)

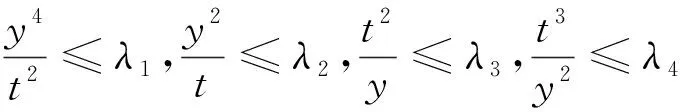
(31)

式(28)、式(29)是双曲不等式，式(27)与式(30)都可以写成如下双曲不等式：

y2≤st,s2≤λ1y

(32)

t2≤sy，s2≤λ4t

(33)

由双曲不等式可以写为二阶锥不等式的性质可知，模型可以重构为一个混合整数二阶锥规划问题，模型有线性目标函数，二阶锥约束，重构后的模型可以使用CPLEX求解得到结果。

4 仿真算例

采用某航空公司一天的运营数据，数据包含120 个航班，26 架飞机，6 种机型，32 个机场，16 473名旅客。机型参数如表2所示。针对既有长时间机场关闭又有飞机故障设置两个场景。设场景一是浦东机场从该日应开放时刻关闭至12:00，机尾号为

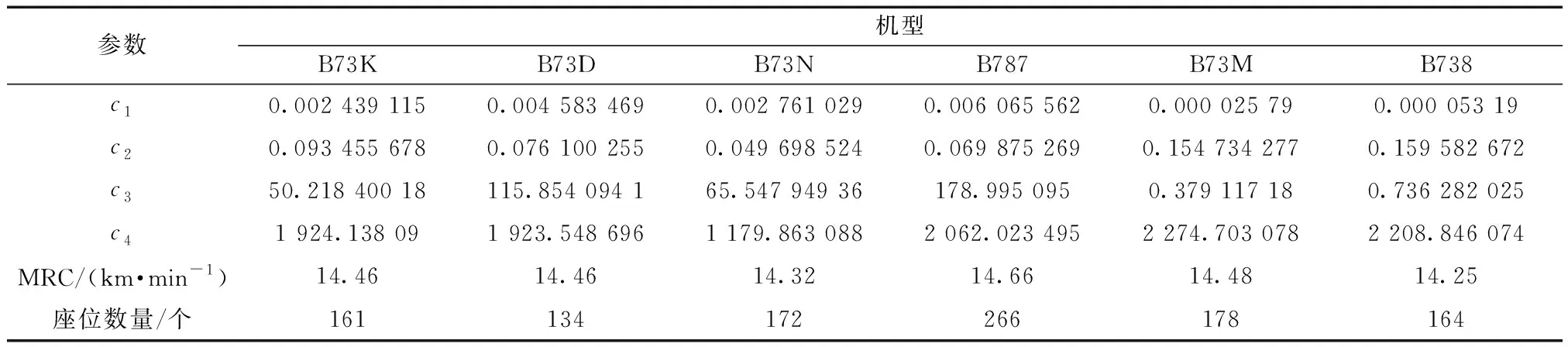
表2 机型的参数

5113飞机故障4 h，分别使用本文模型与不考虑巡航速度控制的模型(即去除速度相关的约束与目标成本)进行求解构成算例1、算例2。场景二是浦东机场从该日应开放时刻关闭至下午16:00，机尾号为5113飞机故障8 h，分别使用本文模型与不考虑巡航速度控制的模型(即去除速度相关的约束与目标成本)进行求解构成算例3、算例4。规定航班最长延误时间为8 h；机组最长执勤时间为14 h，最长飞行时间为8 h；航班之间最短衔接时间为40 min；航班单位运营延误按机型尾流强度分为，重型机4 167元/h，中型机2 916元/h，轻型机208元/h，本文算例中包含中型机 24架，重型机2 架；旅客单位延误经济损失，国内旅客50 元/h，国际旅客100元 /h；机组空闲成本50 元/min。算例信息如表3所示，求解结果如表4所示。

表4 求解结果

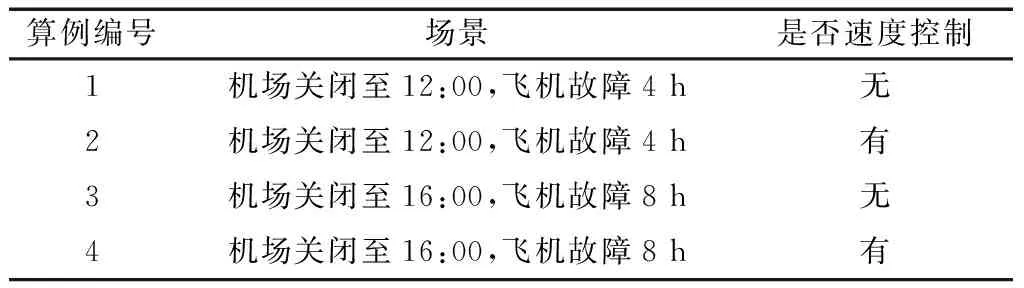
表3 场景算例信息

算例1、算例3与算例2、算例4对比可以看到巡航速度控制的最优成本小于不考虑速度控制。但当恢复场景复杂，受到扰动航班较多，考虑巡航速度控制，恢复成本减少更加明显。图2与图3表示4个算例的旅客延误分布与恢复成本分布，考虑巡航速度控制后算例2较算例1在0～1 h的延误人数减少448人，旅客延误成本减少20 690元，额外燃油成本6 224元，碳排放成本915元。算例4较算例3少取消1班航班，旅客行程取消人数减少52人，客票取消成本46 956元，旅客延误成本减少8 643元。

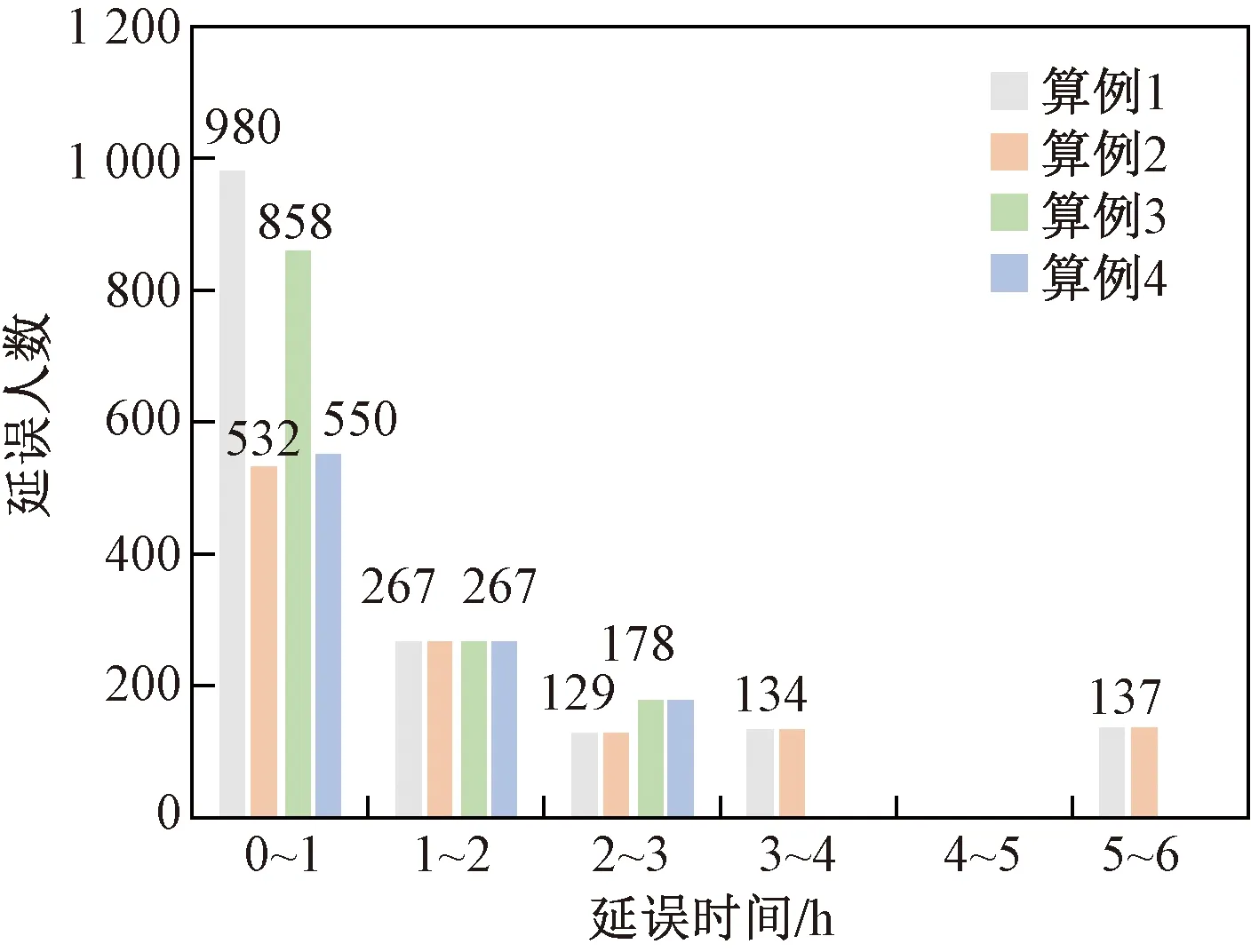
图2 旅客延误分布Fig.2 Passenger delay distribution

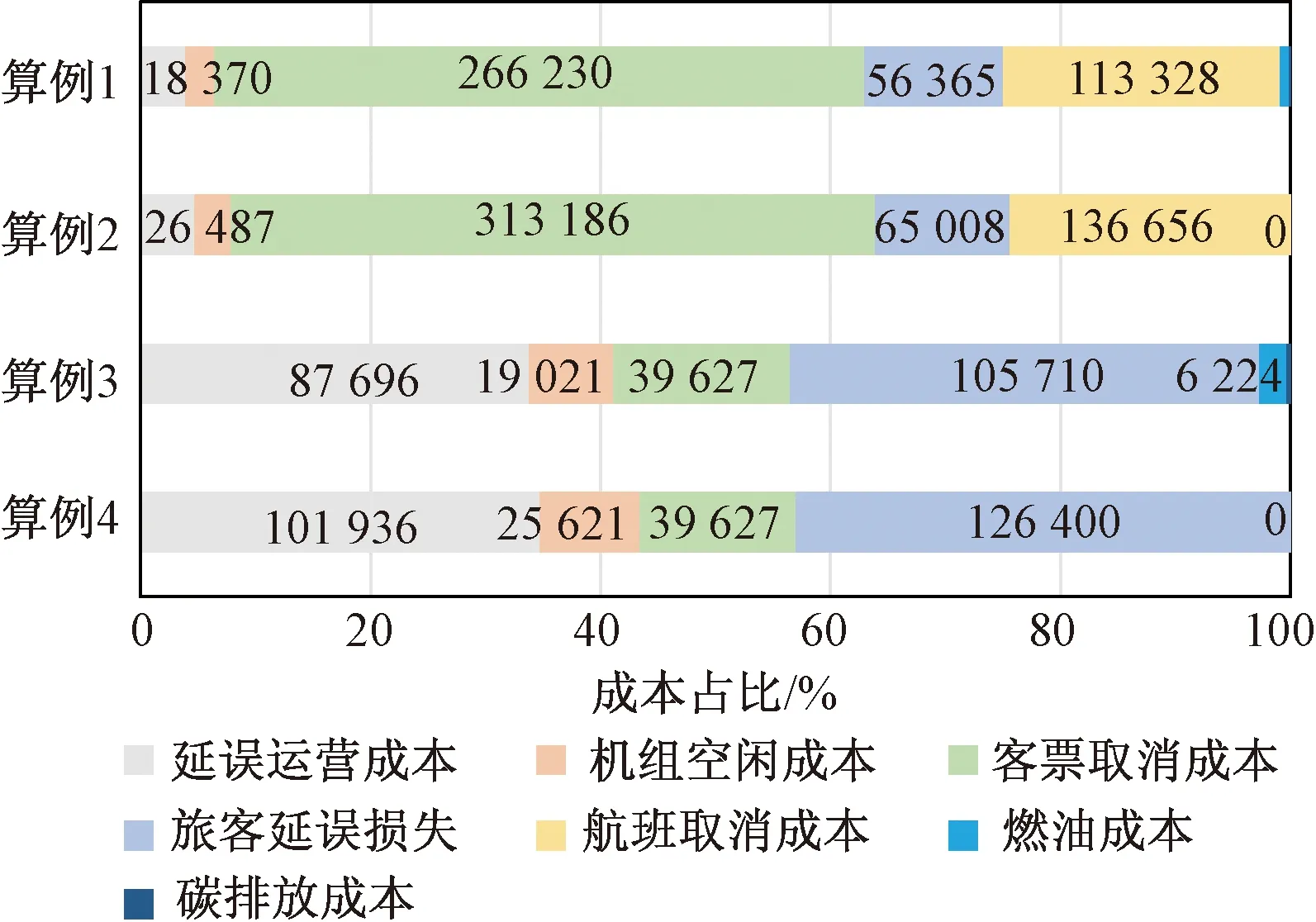
图3 成本分布Fig.3 Cost distribution

各机场的延误情况如图4与图5所示。算例2较算例1将湛江与成都的延误人数清零，在武汉机场的延误人数从788 人降到637 人，武汉机场累计延误时间下降95 min，浦东机场累计延误时间下降22 min。算例4较算例3将成都、曼谷的延误人数清零，武汉机场累计延误时间下降57 min。从成本分布来看，巡航速度控制将等时间的旅客延误成本转化为燃油消耗与碳排放成本，两者之间的差值使总成本减小，而这个差值的大小当受扰航班较多时会比较明显。

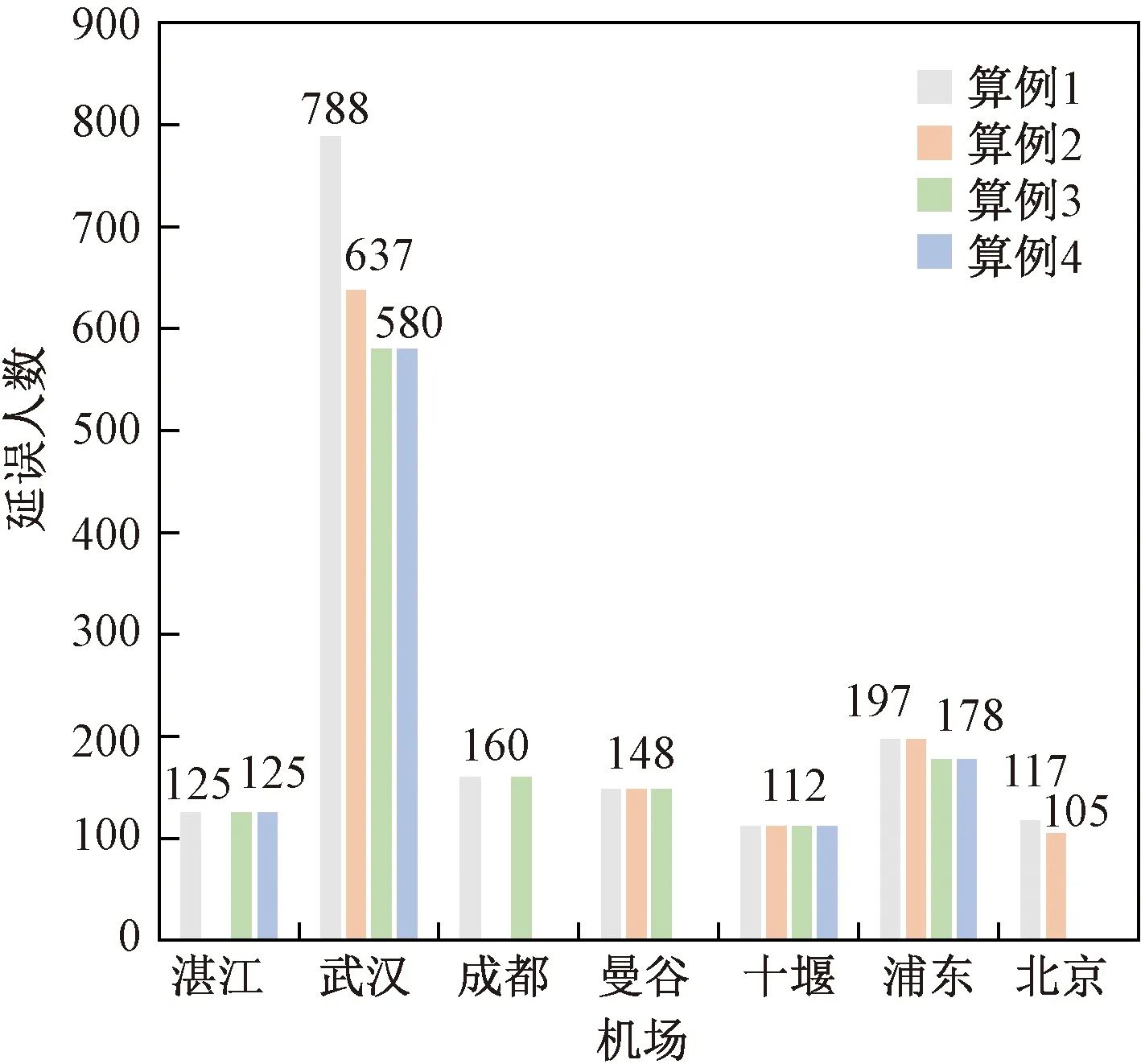
图4 各机场延误人数Fig.4 Delays by airport

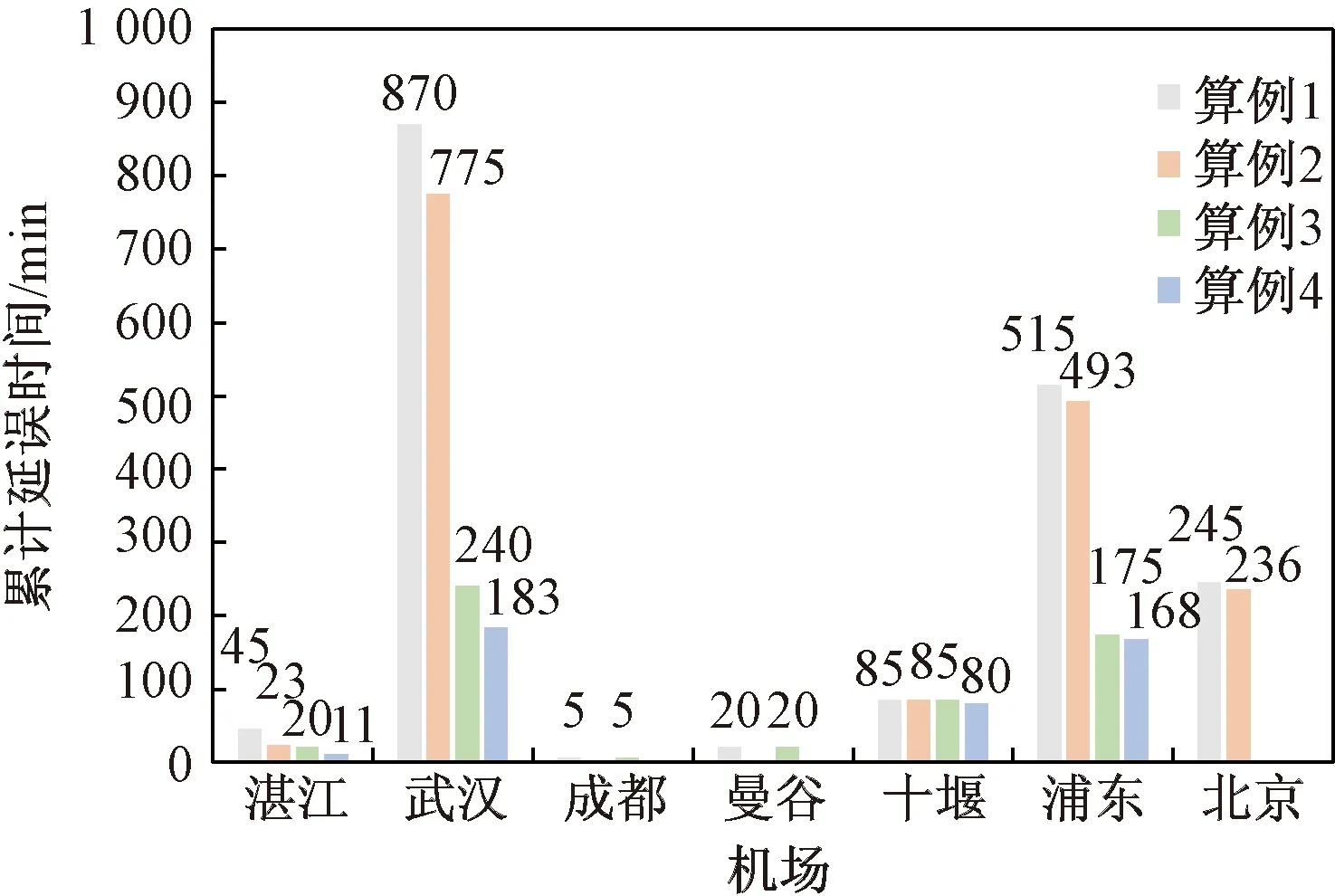
图5 各机场累计延误时间Fig.5 Cumulative delays at airports

5 结论

以航班扰动恢复为目的，考虑飞机、机组、旅客一体化恢复。根据提出的航班网络生成算法，应用改进后的航班网络，将巡航速度控制策略应用于航班恢复建立一体化恢复建立模型。模型易于理解算法容易计算机编程实现，通过扰动场景模拟，可在短时间内获得调整方案。结果表明巡航速度控制策略通过将等时间的旅客延误成本转化为燃油消耗与碳排放成本，在恢复场景复杂，受到扰动航班较多时可明显减少恢复成本，对航班延误恢复问题由一定实际意义。