页岩气水平井产出剖面定量解释方法

樊丽丽, 曾喜喜, 聂园浩, 周新聪, 金 勇

(1.中国石油化工股份有限公司江汉油田分公司石油工程技术研究院， 武汉 433124； 2.武汉理工大学能源与动力工程学院， 武汉 430070)

由于储层低孔特征和极低渗透率，页岩气开发的关键技术是水平井技术和压裂技术[1]。虽然水平井的成本是直井的2～3倍，但是最终可采储量可达直井的6～7倍[2]。自1985年水力压裂开始用于页岩储层增产作业，北美页岩气逐渐形成了以水平井套管完井、分簇射孔、快速可钻式桥塞封隔、大规模滑溜水或“滑溜水+线性胶”分段压裂、同步压裂为主，以实现“体积改造”为目的的页岩气压裂主体技术[3]。水力压裂过程一口页岩气水平井的耗水量(0.67～3.3)万m3[4]。由于自吸作用和重力分离作用，导致压裂水的返排率不足50%[5]，故水平井中有可能存在气水两相流动。尤其开发中后期一旦见水，含水率会急剧上升，严重影响开发效果。在生产过程中，某些产气层出气时可能同时出水，当产层出气较多时，产出层位附近的温度会发生负异常变化；当产层出水较明显时，这时产出层位附近的温度会出现正异常的变化，根据温度的这种变化可以实现对各个层位的产出情况的定性判断。涪陵页岩气田多采用多级压裂分段射孔方式完井，气藏开发与管理者迫切需要了解各层段的产出情况，以实现气藏的合理有效开发。

外国在水平井中下入分布式光纤温度/压力传感器，监测和记录水平井段温度/压力变化。井筒多相流温度的计算模型，通常是根据流体力学基本方程，结合热力学和传热学，通过一定的假设、推导得到。Ramey[6]建立了井筒流体流动的能量方程，得到了适用于注入井和生产井的温度分布计算公式，该模型假设井筒内为稳态导热、地层为径向不稳定导热。Shiu等[7]以Ramey方程为基础，根据现场数据，建立了计算自喷生产井温度剖面的经验公式，可用于两相流体产出物。Sagar[8]根据能量方程，考虑井眼中热传导机理，建立适用于气液两相流动的井筒温度场计算模型，考虑了焦耳-汤姆逊效应的影响。Alves等[9]建立了既可用于管道又可用于任意倾斜角度下井筒流动的温度分布的统一方程式，理想气体或不可压缩液体时可简化为Ramey方程。在垂直井中利用井筒温度和压力模型，对温度和压力录井通过解释可以成功定位气体流入区、流入剖面等[10]。目前学者们对垂直井筒温度模型研究较多，水平井筒的热力学模型研究较少。垂直井和水平井筒模型之间的主要区别在于温度和压力的变化。在垂直井中，井筒温度主要由地热温度决定，随深度而变。水平井的温度在水平段的变化几乎为零，因此建立储层和井筒的温度模型时需要考虑所有微小热能效应，包括焦耳-汤姆逊效应、黏性耗散热和导热[11-12]。

中国由于技术条件及较多地考虑成本因素，温度测井多采用电阻传感器或热电偶式两种。用电缆或者连续油管将温度仪下入井内，测量、记录水平井的井温，可得沿井剖面的细微温度变化，可精确到0.001 ℃。温度测井资料大多用于确定产层温度或注入层温度，了解井内流体流动状态，划分注入剖面，确定产气、产液口位置，检查管柱泄漏、串槽，评价酸化、压裂效果等，对井温测井曲线的应用以定性应用为主。

由于页岩气水平井筒中存在积液、岩屑等，涡轮流量计容易损坏，且多相流量测量技术还处于不断发展中。但是，流体的温度、压力的测量则更容易、更精确，发展温度测井技术是一个重要的方向。通过温度、压力等测量数据确定井筒内的流量分布，可避开多相流量计的使用困境。

生产稳定的水平井，将水平段划分为两个射孔簇之间的管流段以及射孔簇位置的射孔段，分别建立管流能量守恒方程、射孔簇能量守恒方程，在全井所有的管流段、射孔段分别应用能量守恒方程，从而建立全井的产出剖面的解释模型，通过调用MATLAB的lsqnonlin函数，求解模型方程组。将某页岩气井所测得的温度、压力、持气率等数据以及地层等物性参数，应用于该模型，可以验证模型的可行性。

1 管流段和射孔划分

生产稳定的水平井，水平段可以划分为两个射孔簇之间的管流段以及射孔簇位置的射孔，如图1所示，应用时可参考温度变化趋势进行改进。然后分别建立水平井稳态时的气液两相管流能量守恒方程、地层流体流入射孔时的能量守恒方程。

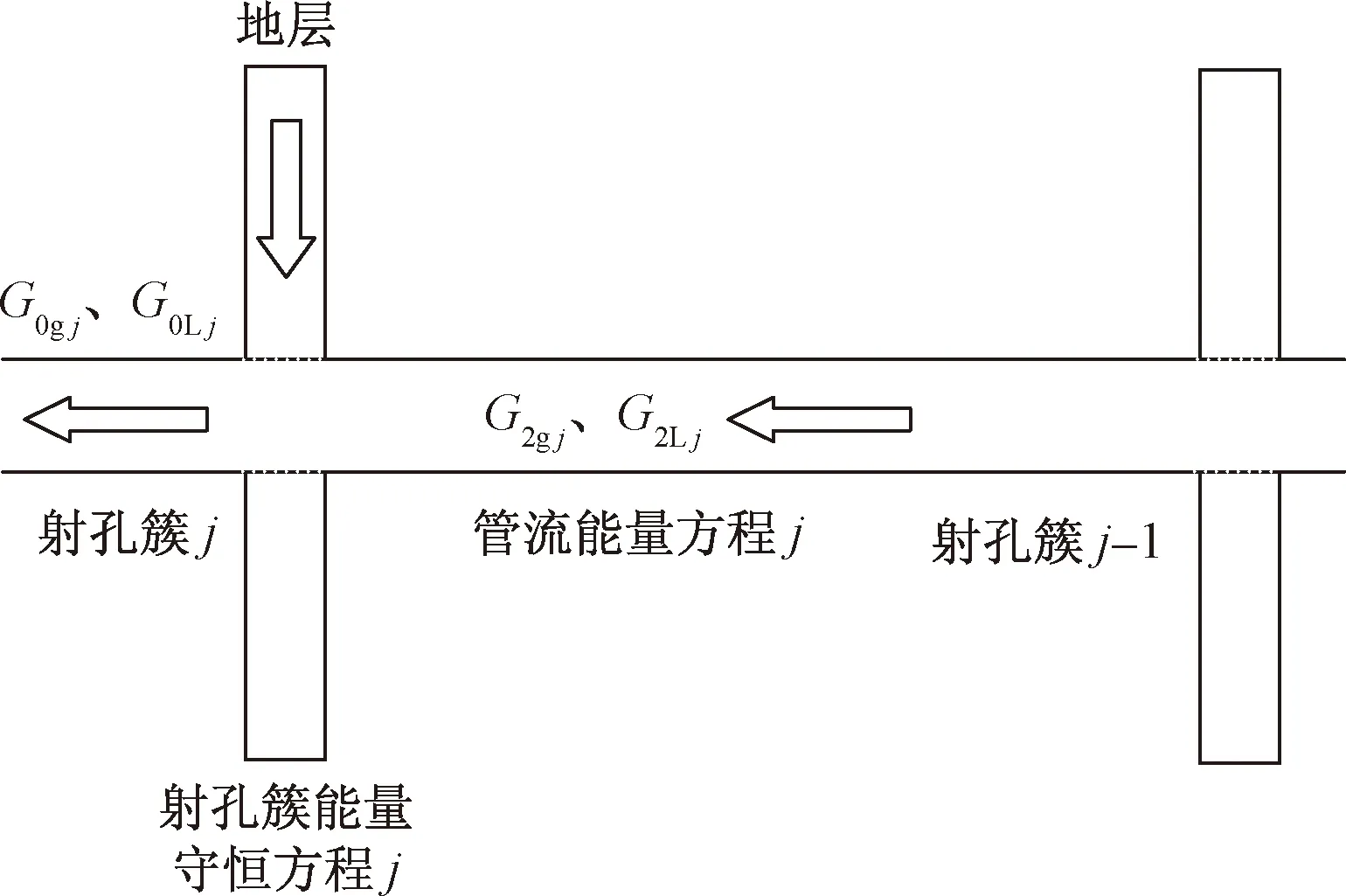
G0gj为第j个射孔簇后的气体流量；G0Lj为第j个射孔簇后的液体流量

2 管流能量方程

流体在管道中流动时，不断地与周围介质进行热交换。流体的温度变化与势能变化、动能变化、热交换和焦耳-汤姆逊效应等有关。主要假设条件：混合物在管道中的流动状态为是一维稳定流动，不计流体的径向温度梯度；井筒内传热为稳定传热，地层传热为不稳定传热，且服从Remay推荐的无因次时间函数；管道的横截面积A不变；假设两相之间没有温度滑移，计算控制体内，气液相具有相同的温度；不考虑相变热[13]。

取管段dx为研究对象，如图2所示，根据能量守恒定律，对于控制体内混合流体存在的热力学关系[13]：环境传入控制体热量=流出控制体能量-流入控制体能量+控制体内能量的积累。

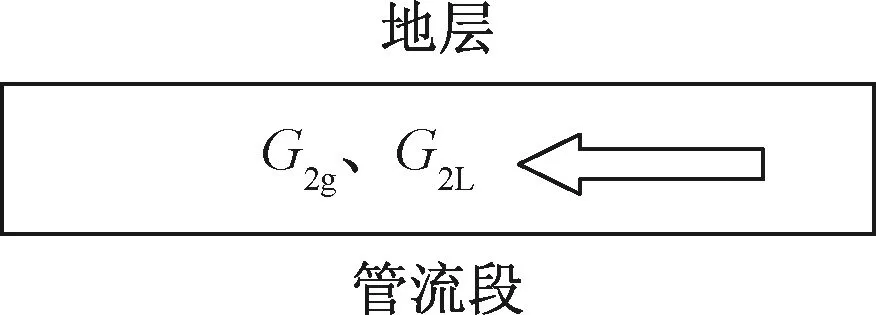
图2 取dx段井筒进行能量分析Fig.2 Energy analysis of dx differential well bore

则气液两相的稳态管流的能量方程为

(1)

式(1)中：x为流体流动方向的水平井长度，m；ρ为流体的密度，kg/m3；w为流体的流速，m/s；H为截面含率；h为流体的焓，J/kg；g为重力加速度，m/s2；S为高程，m；A为截面积，m2；Q为井筒向地层的传热量，J；下标g代表气体，L代表液体。

其中，Hg+HL=1。混合流体质量流量为

Gm=Gg+GL=ρgwgHgA+ρLwLHLA

(2)

式(2)中：G为流体的质量流量，kg/s；下标m代表气液两相混合流体，其余同前。

对于气体有

(3)

对于液体有

(4)

式中：cp为流体的定压比热容，J/(kg·K)；T为流体温度，K；p为流体压力，Pa；αJTg为气体的焦耳-汤姆逊效应系数，K/Pa；其余同前。

井筒流体向周围地层岩石传热，首先要克服油管、油套环空流体、套管、水泥环产生的热阻，光套管生产时，井眼径向传热如图3所示。

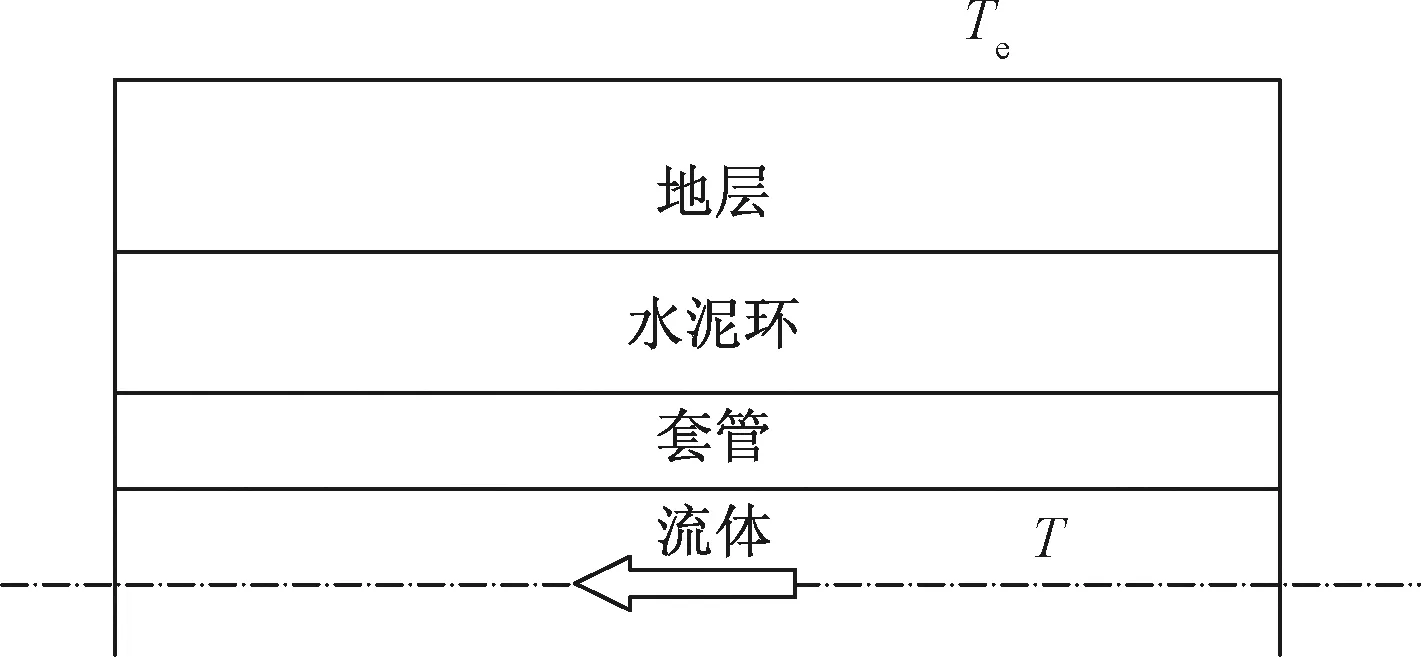
图3 井眼径向传热Fig.3 Radial heat transfer in borehole

从流体到固井水泥/岩面界面，单位井段从流体到固井水泥/岩面界面的传热过程为径向稳定传热，从水泥环/岩石界面到地层内传热为二维非稳定问题，应用Ramey推荐的无因次时间函数简化为一维问题，最后可得流体与地层之间的径向热传递是热流梯度方程[14]为

(5)

式(5)中：rto为井眼半径，m；Uto为井眼的传热系数，W/(m2·K)；ke为地层的导热系数，W/(m·K)，下标e代表地层；T为温度，K；f(tD)为地层的瞬时导热函数，即Ramey无因次时间函数，可用哈桑-卡皮尔(Hasan-Kabir) 1991年提出的公式计算，tD为无因次时间；其余同前。

式(2)、式(5)代入式(1)得到管流能量方程为

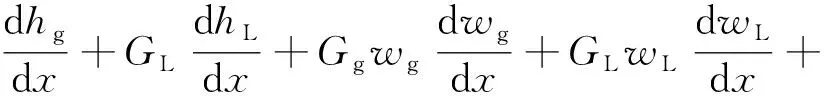
(6)

3 射孔处能量守恒方程

对于气液两相的情况，射孔处的地层-井筒能量守恒的物理模型如图4所示。根据图2和图4，对比管流和射孔簇的物理结构，可知射孔簇能量守恒模型应该是，在管流模型的能量变化的基础上，再叠加上射孔处的能量流入。

G0g、G0L分别代表射孔簇下游的气体、液体的流量；G2g、G2L分别代表射孔簇上游的气体、液体的流量；G1g、G1L分别代表从地层流入射孔簇的气体、液体的流量

对于水平井，一簇射孔处的总长度在1～1.5 m，所以不考虑势能以及动能的变化，则对射孔处的井筒和地层的能量守恒为：进入井筒的流体携带的能量-流出井筒的流体携带的能量+从射孔处流入井筒的流体携带的能量+地层向井筒导热的径向热传递=0。

则射孔簇气液两相地层-井筒能量守恒方程为

(7)

式(7)中：l为射孔簇的长度，m；T02为射孔簇的流体温度，为下游、上游的平均温度，K；下标2为射孔簇上游流入的流体，下标1为地层流入射孔簇的流体，下标0为射孔簇流出的流体；下标i=L，g分别代表液相、气相；其余同前。

根据质量守恒，可以得到

G2g=G0g-G1g

(8)

G2L=G0L-G1L

(9)

将式(8)、式(9)代入式(7)，则能量守恒方程为

(10)

式(10)中：焓差可以根据式(3)、式(4)求得。

4 全井剖面解释模型及求解方法

4.1 全井剖面解释模型

在全井所有的管流段、射孔段，如图5所示，分别应用管流能量方程(6)、流体流入能量守恒方程(7)，从而建立全井的产出剖面的解释模型为

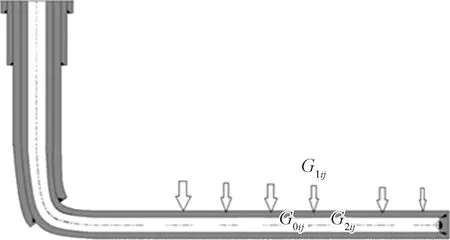
图5 全井的示意图Fig.5 Schematic diagram of the whole well

(11)

(12)

式中：i=L,g；下标j为射孔簇编号，j=1，2，…，N-1，N为射孔簇的总数；G2gj=G0gj-G1gj，G2Lj=G0Lj-G1Lj，其余同前。

由于质量流量是守恒的，可分别对各段管流段方程(11)进行积分，得第j个射孔簇的上游管流能量方程积分形式。

根据质量守恒，可以得到

(13)

(14)

式中：Ggtotal、GLtotal分别为井内气、液的总产量，kg/s。全井的产出剖面上N个射孔数，各射孔簇产气量、产水量未知，总共2N个未知量。模型中，式(11)～式(14)中，管流能量方程有N-1个，射孔能量守恒方程有N-1个，质量守恒方程2个，总共有2N个方程，形成封闭方程组。其中，温度、压力、持气率采用连续油管测试。各个积分段，可以根据沿水平段所测温度、压力、持气率数据，选择相应的地质参数、井眼轨迹，进行数值积分。通过调用MATLAB的lsqnonlin函数，可以求解该方程组，实现水平井产出剖面流量的定量计算。

4.2 求解方法

MATLAB的lsqnonlin函数的目标问题模型为

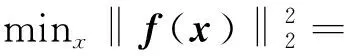
(15)

式(15)中：

(16)

调用该函数可以求解上述2N个方程组。

该解释方法适用于水平井射孔完井的情况。流体的温度、压力等的测量较容易、精确，应用该方法确定水平井中各射孔簇流量时较为实用。

5 现场应用

某页岩气水平井的水平段深度3 300～3 600 m、长度约1 300 m，射孔簇有47簇，井眼轨迹如图6所示。从井口下入仪器，测量得到了井筒内流体的温度、压力、持气率分布图，该井水平段随井深的压力曲线、温度曲线、持气率曲线，分别如图7～图9所示。

图6 某页岩气井水平段井眼轨迹Fig.6 Well trajectory of horizontal section of a shale gas well

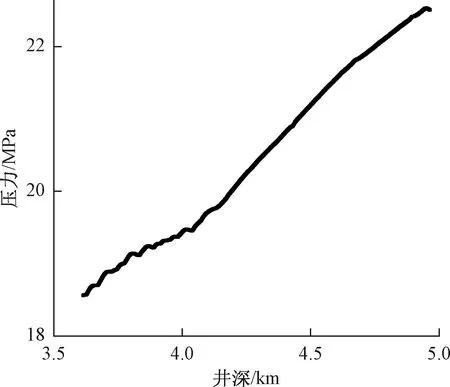
图7 某页岩气井随井深的压力曲线Fig.7 Pressure curve of a shale gas well with well depth

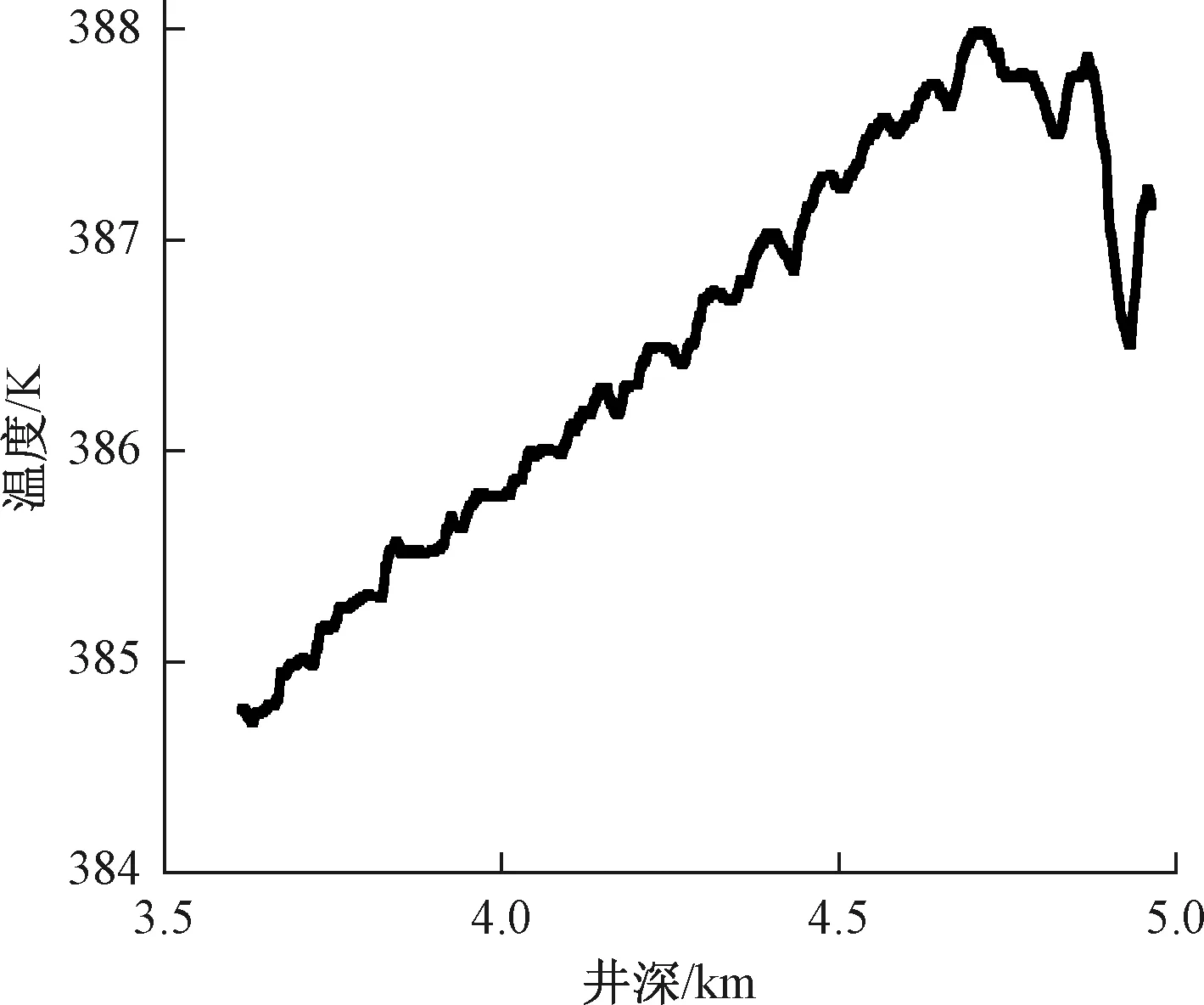
图8 某页岩气井随井深的温度曲线Fig.8 Temperature curve of a shale gas well with well depth

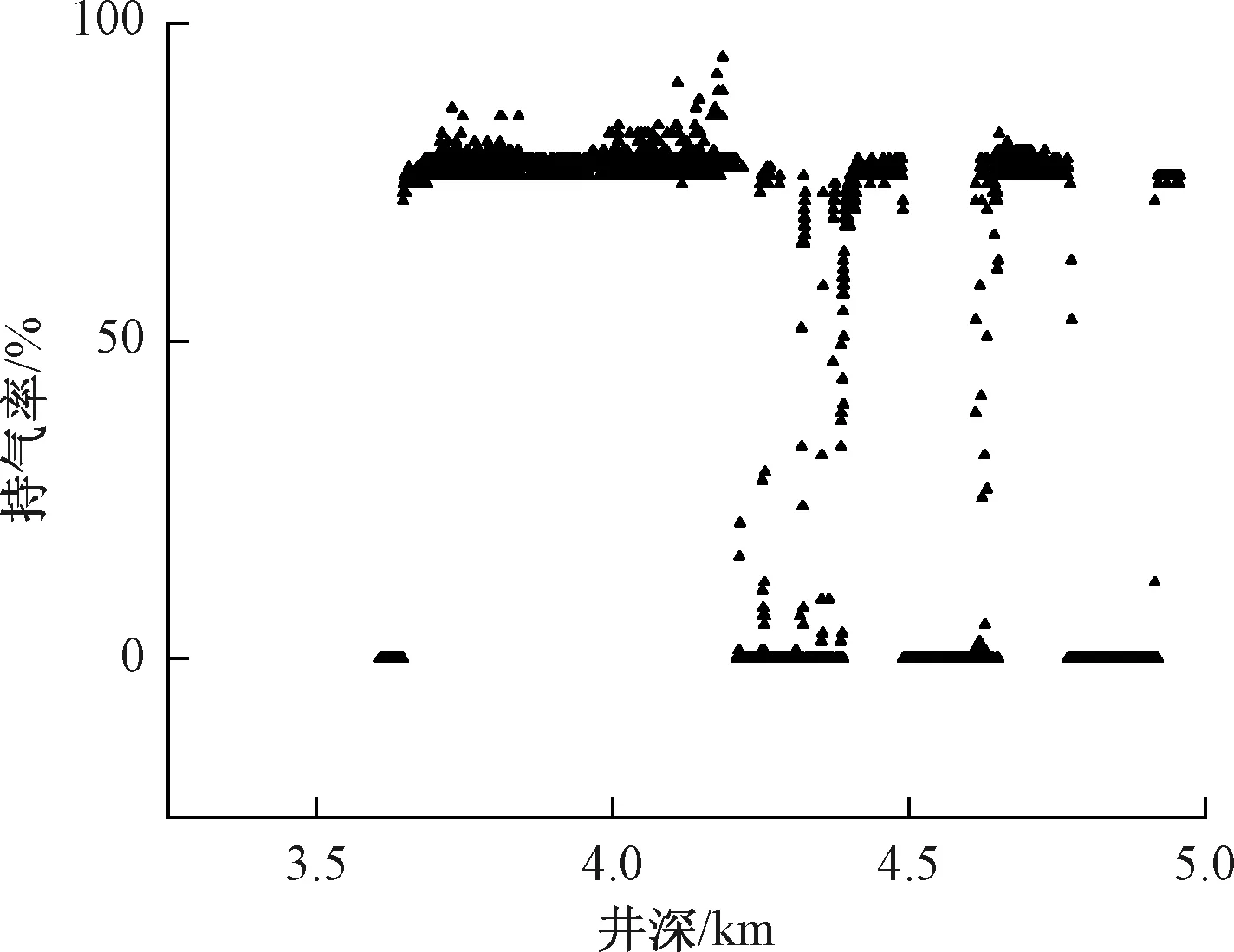
图9 某页岩气井随井深的持气率曲线Fig.9 Gas holdup curve of a shale gas well with well depth

气田地层的地温梯度0.03 ℃/m，地层压力系数0.015 5 MPa/m，导热系数0.865 35 W/(m·℃)，地层热扩散系数7.5×10-7m2/s，气井的水泥环导热系数1.6 W/(m·℃)，套管的导热系数58.15 W/(m·℃)，井眼直径215.9 mm，套管外径139.7 mm，套管内径118.6 mm，天然气相对密度0.564，地面产水量44 m3/d，产气量4.5×104m3/d。

应用全井剖面解释模型及求解方法确定了47簇位置射孔的产气和产水量，通过归一化变换给出全井各簇的产气量和产水量分布的质量百分比柱状图如图10所示，模型中94个方程的函数值分布如图11所示，其中射孔处的能量守恒方程的函数值分布较集中，都趋于较小，管流能量方程的函数值分布较分散，个别偏大；管流能量方程比射孔处能量守恒方程涉及的影响因素要更多。采用的单位都是国际单位，能量模型中函数值的单位为焦耳，绝对误差平均值为95 J，能够满足工程应用的要求。

图10 某页岩气井解释结果(各簇产气和产水量百分比)Fig.10 Interpretation results of a shale gas well (gas production and water production percentage of each cluster)

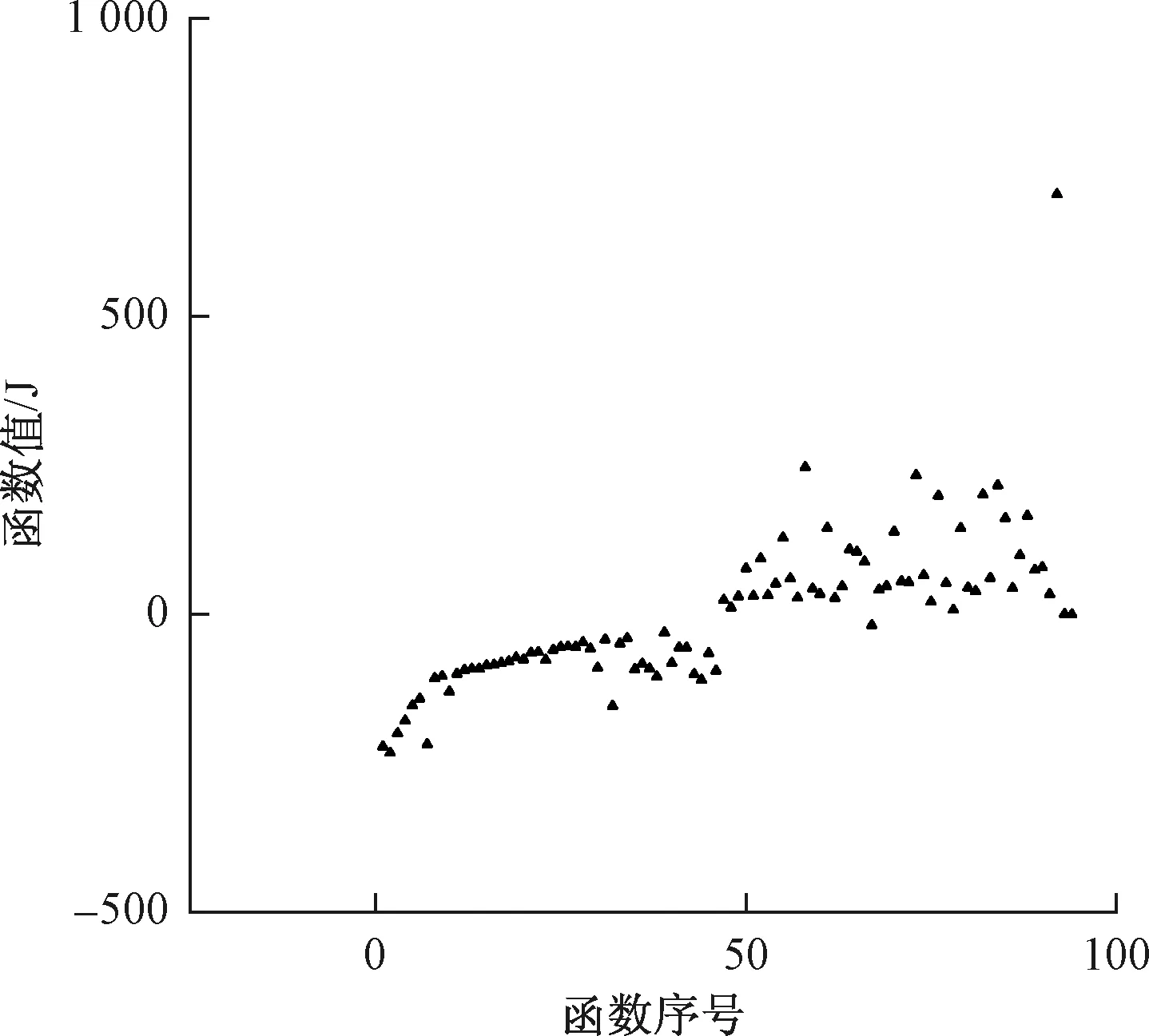
图11 94个方程的函数值分布图Fig.11 Function value distribution of 94 equations

该井眼轨迹向下倾斜严重，垂深变化接近 200 m，压力从水平井的趾端向跟端逐渐降低，较为明显，静压差影响较大，解释结果可以看到主要在靠近跟端的部分产水；各射孔簇的气体产量较大，在各射孔簇附件的焦耳-汤姆逊效应引起的降温效果明显；在各管流段由于上游射孔簇产水以及管流段的地层传热的影响，温度变化趋势较缓。地层温度随着垂深减小而降低，另外井筒内压力降低，井筒内气体的焦耳-汤姆逊效应引起降温，则水平井的温度趋势是逐渐降低的；由于气流逐渐增大，持气率在靠近跟端较大，水平段靠近趾端也有产水，靠近趾端的持气率有些段较大，有些段较小，井底有积水，但是有些簇产气量也较大。

6 结论

(1)对于生产稳定的水平井，水平段可以划分为两个射孔簇之间的管流段以及射孔簇位置的射孔段，分别建立水平井稳态时的气液两相管流的能量守恒方程、射孔段处流体流入时与地层之间的能量守恒方程。

(2)在全井所有的管流段、射孔段分别应用管流能量方程、射孔簇流体流入能量守恒方程，从而建立全井的产出剖面的解释模型。

(3)根据沿水平段所测温度、压力等数据，选择相应的地质参数、井眼轨迹，应用全井的产出剖面的解释模型，调用MATLAB的lsqnonlin函数，实现水平井产出剖面的定量计算，模拟结果可以满足工程应用要求。

(4)该方法通过在涪陵页岩气井产气剖面测试中应用实践，可以为压裂施工效果评价、后续改造措施等提供有效的参考依据。

(5)该方法需要注意的是地层的地质参数、传热参数，对计算结果会产生影响，需要准确确定。