五盂高速公路顺层岩质边坡变形破坏模型试验

王 海, 张梓钦, 杨国香*, 张 彬, 徐能雄, 石 盼

(1.山西省交通规划勘察设计院有限公司， 太原 030012； 2.中国地质大学(北京)工程技术学院， 北京 100083)

顺层基岩导致的滑坡是山区及丘陵地区高速公路等工程建设中常见的地质灾害，也是基础设施工程建设中时常面临的重大难题。道路及路基工程建设中，大规模的岩土开挖不可避免，由此易形成高陡边坡，加之集中降水的影响，极易形成滑坡灾害。而顺层滑坡一般具有规模大、破坏力强等特点，对工程及环境破坏严重，且勘察设计、处治技术难度大，费用高昂，时至今日，已给工程建设和人居环境造成极大的影响和灾害。例如，2009年“6·5”重庆武隆鸡尾山崩滑灾害[1]造成了10人死亡，64人失踪，8人受伤的严重后果；2003年7月13日，三峡水库区千将坪发生大规模滑坡[2]，导致当地14人死亡，10人失踪，近千人受灾，直接经济损失高达 5 735万元。因此，顺层岩质边坡破坏机理具有非同小可的研究意义，这对于科学预测边坡破坏范围，及时提出对应的预防护加固手段以及如何提升高速公路边坡整体防护水平，都具有重要的工程指导作用。

此外，软弱夹层对边坡的变形破坏往往起关键性的作用。马晓辉等[3]整理了大量新安江大坝右岸坝基薄层页岩的观测试验资料，总结得到矿物、化学成分、结构构造以及渗流对软岩性状变化的评价准则。李守定等[4]依据宝塔滑坡区试验结果分析了泥化夹层的形成条件，说明了泥化夹层是滑坡发生的主要原因。Xia等[5]对三峡库区的石榴树包滑坡长达6年的现场监测数据研究表明，浅层滑体变形的主要控制因素为降雨，而深层滑体的稳定性主要受库水位变动影响。依据现场监测数据的研究对滑坡临滑预报具有重大意义，然而缺乏系统性的监测手段，难以深入探究滑坡形成的机理和条件。而对坡体组分的物理化学性质研究有利于揭示坡体内部结构，分析滑坡成因，但难以对滑坡运动过程进行阐释。

随着信息技术的普及和迅速发展，各类数值模拟方法在研究顺层岩质边坡变形破坏机理中的重要性也日益凸显。吴顺川等[6]建立了含软弱结构面土质边坡的离散元颗粒模型，对其进行变形破坏模拟，提出了分析软弱夹层发展机理的新方法。黄润秋等[7]用FLAC3D建立了汤屯高速公路边坡模型，分析其开挖后的应力应变特征，结果表明，坡体中上部沿软弱结构面滑动，边坡的变形主要受岩体结构和层间软弱夹层的控制。何铮等[8]通过人工合成地震波并建立了边坡的三维地震反演模型，揭示了顺层岩质边坡在地震作用下渐进变形的破坏机制。林杭等[9]使用FLAC3D模拟了层状边坡的破坏过程，通过强度折减法分析了结构面倾角对边坡稳定性的影响。张社荣等[10]以萨尔玛条分法和强度折减法为手段研究了层状岩质边坡的破坏规律，结果表明，岩层倾角和坡角对边坡稳定性的影响较大，结构面间距影响较小，且两种方法计算结果相近。邓荣贵等[11]提出了顺层边坡稳定性评价和失稳长度分析的新方法，并将其应用于319国道和渝怀铁路的边坡分析中，证明了分析方法的可靠性。高永涛等[12]基于离散单元法研究了270个边坡模型，总结了4种顺层岩质边坡的破坏形式，分析了结构面倾角和边坡角两个参数在边坡稳定性分析中起到的作用，并得到其与边坡安全系数的关系。但由于其对参数和本构模型准确性的过分依赖，数值模拟方法仍缺乏其作为单独分析方法时的可靠性。而物理模型试验能够很好地再现滑坡变形破坏发展的全过程，且便于进行系统性的监测，已成为研究滑坡变形破坏机理的成熟方法。

现以山西五盂高速公路顺层岩质边坡为原型，依据相似理论建立大型二维物理模型。并采用SAA阵列式位移计、三维激光扫描仪、摄影测量技术和人工变形测量相结合的方法进行监测，建立立体式综合性的位移监测系统，进行覆盖坡体内部和外部位移的测量。同时采用数值模拟手段，在宏观上进一步揭示和验证边坡变形破坏的机理。

1 模型试验设计

1.1 工程概况

研究的滑坡原型为五盂高速K23+760滑坡，该滑坡体处于两条冲沟之间，冲沟构成了滑坡体的侧面边界，滑坡体平面形态为不规则椭圆形，总面积0.180 km2，滑体主轴方向为245°，滑体厚度范围10～35 m不等，平均厚度约为20 m，总体积约为 3 600 000 m3，如图1所示。坡体地形陡缓交替，在变形及人工改造影响下形成多级平台，局部形态呈折线型。坡面草本植物较发育。滑体成分主要为强风化的黑云斜长片麻岩及绢云母片岩，岩体较为破碎，强度低，岩芯多呈碎块或薄片状；滑体表层2～5 m部分为残坡积粉质黏土和碎石土，且堆积松散。选取该滑坡体为研究对象，开展开挖和降雨导致顺层岩质滑坡的变形演化规律及孕灾机制。

图1 五盂高速公路滑坡示意图Fig.1 Sketch of landslide on Wuyu Expressway

1.2 物理模型建立

1.2.1 模型概化

二维物理模型原型选择K23+874断面，依据滑坡体结构特征，将原型概化为东西长400 m，南北宽100 m，高度为200 m的区域，区域内坡角为23°～26°，岩层倾角约为25°，并存在深度为4～6 m的绢云母层软弱带，依据概化的坡体制作一定厚度的平面应力模型。综合考虑阵列式位移计(SAA)等监测设备的尺寸和精度以及试验研究范围、模型制作等条件，最终选取相似比为100，即模型箱尺寸定为400 cm×100 cm×200 cm，同时在距坡表面30～60 cm深处设置软弱夹层，厚度为3 cm。为分别模拟单层软弱结构层和双层软弱结构层的顺层岩质滑坡，分别设计两个模型试验组A、B。

1.2.2 相似条件与模型材料

因模型相似材料自身容重满足重力梯度条件，容重比选取为1即可。再由相似理论推导得到模型材料各相似常数。应力σ、抗剪强度τ、弹性模量E相似常数为

Cσ=Cτ=CE=100

(1)

应变ε、泊松比μ、内摩擦角φ相似常数为

Cε=Cμ=Cφ=1

(2)

坡体主要岩体的相关物理力学参数如表1所示，模型试验选取的相似材料对应参数则如表2所示。

表1 边坡主要岩体的物理力学参数

经过常用材料的对比，最终选取重晶石粉和石英砂为骨料、石膏为胶结剂以及甘油作为掺加剂，以制备目标黑云斜长片麻岩的相似材料，采用4因素6水平的均匀试验设计方法，以实现表2中列出的目标属性。对于每个配比组合，制作10个直径为50 mm，高度为100 mm的圆柱体试样(图2)并测试其密度、抗压强度、内聚力和内摩擦角。制备控制室温为(20±2)℃，湿度为60%±10%。测试中需要保证最大限度满足主要物理力学性质近似要求，尽可能满足次要物理力学性质近似要求。结果发现，该材料的质量比例为48∶35∶9∶2(重晶石粉∶石英砂∶甘油∶石膏)时，对应物理力学性质如表3所示，符合相似材料要求。由此确定该组合物即可用于作为目标黑云斜长片麻岩的相似材料。另外，试验发现，原型中的绢云母层具有遇水软化及强度降低的特点，据研究表明，马兰黄土遇水后也会有类似的强度降低的特点，因此模型试验中采用铺设一定厚度的马兰黄土来模拟软弱夹层。

表2 目标材料物理力学参数

图2 圆柱体试样Fig.2 Cylinder test sample

表3 相似材料物理力学参数

1.2.3 模型制作

设计模型箱尺寸为400 cm×100 cm×200 cm，模型箱侧壁采用透明有机玻璃材料，可作为可视窗口，便于实时观测试验过程滑坡体变形情况。采用分层夯实法进行模型砌筑，保证每层模型材料厚度均为20 cm，坡度为25°。砌筑时将每层体积所对应质量的相似材料夯实到模型箱中，填满预定的分层，并保证模型材料密度为2.3 g/cm3。为模拟岩层层理，在层与层之间撒上厚度为2 cm左右的干重晶石粉，确保坡体模型分层砌筑。

A组模型在高度170 cm处设置两根预制水管，分别距坡体两侧侧壁25 cm。两根预制水管长度均为170 cm，顺层面铺设，预制水管近坡顶端连接注水口，且每隔15 cm设置直径4 mm的出水孔，水管末端封闭处理。模拟过程中通过控制注水口阀门模拟降雨，水流通过水管出水孔渗透至模型各处，以此来模拟雨水在软弱夹层中的渗流。随后在水管上部铺设厚度为5 cm的干燥马兰黄土以模拟软弱夹层。

B组模型在高度170 cm处时，铺设第1层厚度为5 cm的黄土软弱层，其上再铺设厚度15 cm的模型材料。随后设置3根预制水管，其中两根顺层面设置，分别距坡体两侧侧壁25 cm，一根顺坡体走向设置于模型坡顶处。第2层黄土软弱层铺设于预制水管上部，厚度为5 cm，顺层面铺设。最后以密度控制法铺设模型材料至模型预定高程。A、B组试验模型三维图如图3所示。

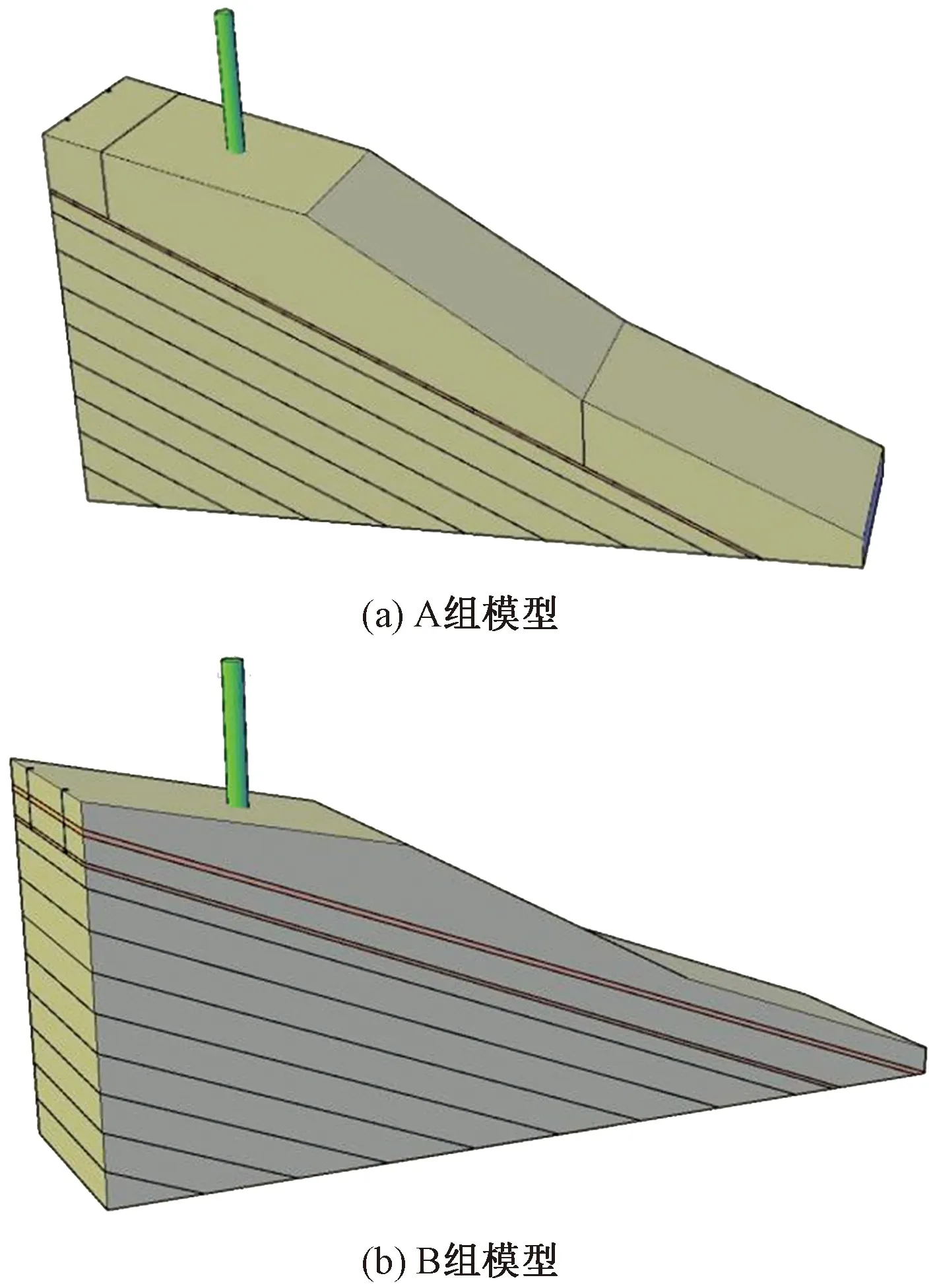
图3 试验模型三维图Fig.3 3D diagram of test model

1.3 测试方案及监测

1.3.1 试验方案

A组为含单一软弱结构面顺层岩质边坡模型，首先对其进行分步开挖模拟，整个试验过程分5次开挖。第1次开挖从坡脚到坡体内部，总进尺 23 cm，监测并确保坡体无位移后进行第2次开挖；第2次开挖范围为软弱结构面以上岩体深度 45 cm；第3次开挖沿第2次开挖面竖直向下开挖至模型底面，监测并确保稳定后进行第4次开挖；第4次开挖范围为软弱面上方岩体，开挖深度45 cm，最后一次开挖沿第4次开挖界面竖直向下开挖至软弱面，开挖完成后及时进行监测。开挖步骤如图4所示。

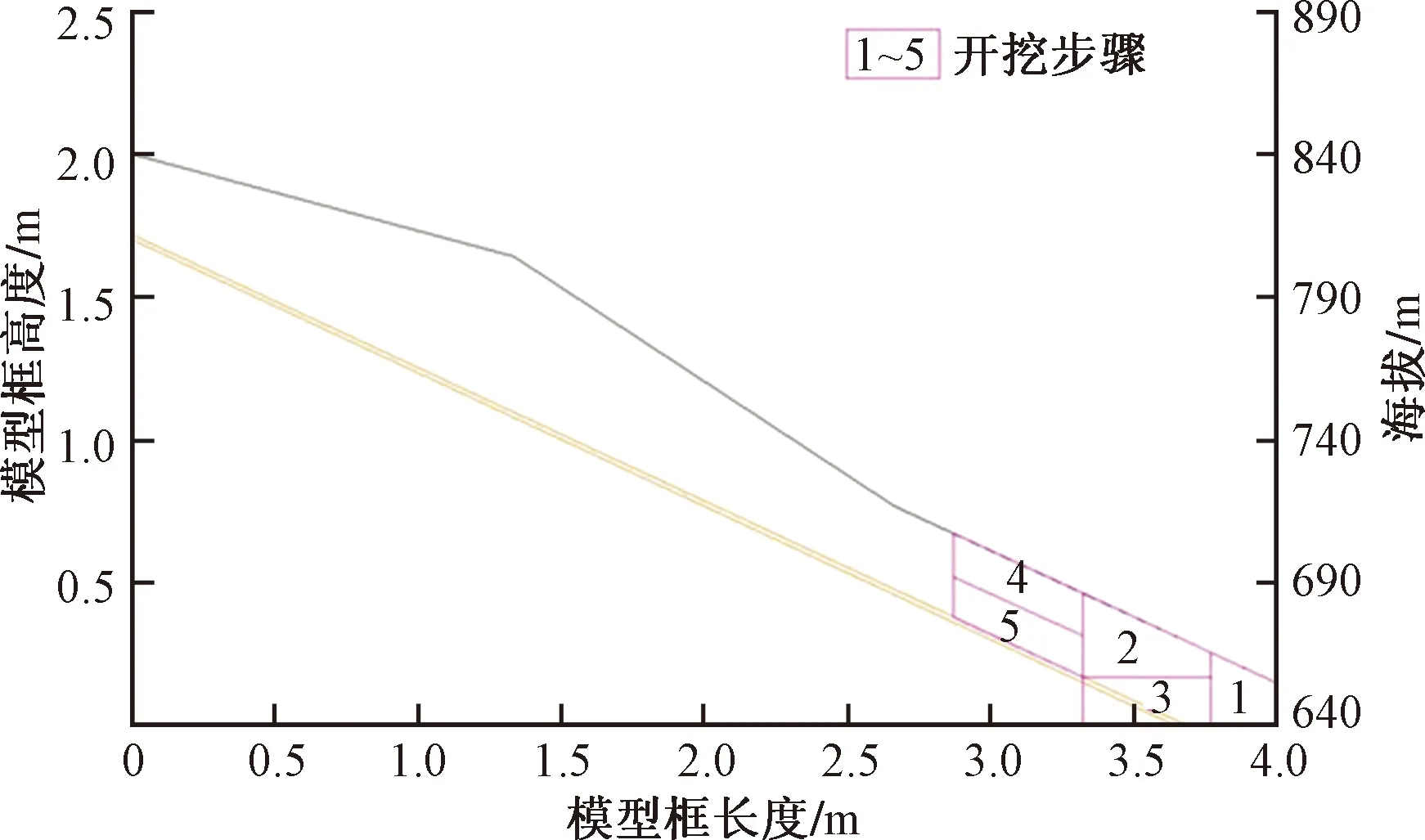
图4 A组模型开挖步骤Fig.4 Model excavation steps of group A

开挖步骤结束后开始降雨模拟，对预制水管进行注水，与此同时进行水量监测。根据边坡模型表面积和注水量可以计算得到模拟降雨量。第1次降雨模拟的降雨量为5.5 mm/d，模拟单层软弱结构面顺层岩质边坡在小雨下的状态。第2次降雨模拟的降雨量为15 mm/d，模拟程度为中雨。第3次模拟大雨下的边坡状态，降雨量为30 mm/d。降雨停止后，继续对模型边坡变形进行监测，直至边坡位移不再增大，试验结束。

B组为双层软弱结构面顺层岩质边坡模型，首先进行开挖模拟，开挖进尺为60 cm。待坡体没有明显滑动15 min后开始降雨模拟，降雨模拟流程与A组一致。

1.3.2 监测布置

采用阵列式位移传感器(SAA)监测坡体内部位移，SAA布置于距坡顶水平距离80 cm，高度 2.5 m 处；采用三维激光扫描仪监测坡面位移，三维激光扫描仪布置于模型坡面正前方2 m处，高度1.8 m处，如图5所示；采用摄影测量技术监测模型边坡整体的变化情况。试验开始前先将模型箱侧壁进行坐标网格划分，划分网格大小为20 cm×20 cm。在试验过程中，以坐标网格为参照对预先埋置的染色小立方体块进行绝对位移测量，然后对试验过程进行摄影监测，摄影时确保每两张相邻照片的重叠度在2/3以上。最后统计整理试验不同阶段各染色小立方块体的相对位移关系，绘制得到边坡侧面相对位移图，进而分析模型侧面变形量。

图5 模型边坡及摄影测量控制点Fig.5 Model slope and photogrammetric control point

2 试验结果及分析

2.1 A组试验结果

2.1.1 SAA位移监测分析

阵列式位移计SAA监测结果显示，边坡模型坡表面的X方向(边坡走向)累计位移为18 mm，Y方向(顺坡方向)累计位移为-97 mm；在软弱结构面处，X方向累计位移为5 mm，Y方向累计位移为-78 mm。图6(a)表示X方向位移沿SAA从坡体表面向坡内变化不大，在坡体表面和软弱结构面处的偏移方向相反，且偏移量较小，表现为无明显规律性；图6(b)表示坡体表面的Y方向位移量最大，向坡体内部逐渐减小。边坡累计位移如图6所示，测量位移与时间关系如图7所示。

图6 SAA累计位移Fig.6 SAA cumulative displacement

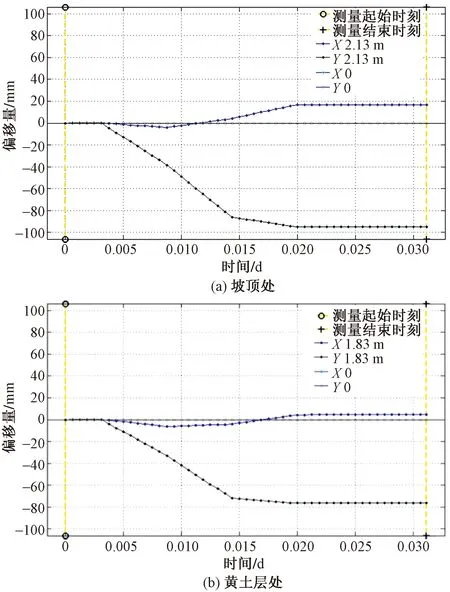
图7 位移与时间关系Fig.7 Displacement versus time

2.1.2 三维激光扫描仪监测数据分析

首先用Trimble TX8三维激光扫描仪获取试验过程中不同状态下的坡体表面点云数据，通过点云处理软件cyclone进行建模和数据处理，使用MATLAB对数据量过大的模型进行适当抽稀。以第1次扫描得到的点云数据为基础，用之后各次扫描结果与之进行差值计算，以此作不同状态下的模型边坡沉降图，如图8所示。

图8 模型边坡沉降Fig.8 Model slope settlement

据沉降图显示，对模型边坡进行5阶段开挖后，边坡无明显沉降。模拟降雨时开始出现沉降，且模型边坡的沉降量随降雨量增加而增加。坡脚位置首次发生滑塌是在模拟小雨状态下，滑塌位置为坡体Y轴方向-1.25～-1.5 m处，沉降值均在0.2～0.25 m范围内；模拟中雨状态下，滑塌范围扩大至Y轴方向-1.5 m处软弱结构面以上的全部岩体，沉降值均大于0.2 m；模拟大雨状态下，坡体滑塌范围再次扩大，Y轴方向-2.5 m处软弱结构面以上全部岩体下滑，沉降值均大于0.2 m。

2.1.3 人工摄影测量数据分析

根据预先在模型箱侧面玻璃板设置的坐标网格，通过摄影监测测量各立方块在不同阶段下的绝对坐标，将其标记在CAD图中，并把滑动前和滑动后坐标进行指向性连接即可作边坡的位移矢量及趋势图，如图9所示。

图9 单层软弱结构面顺层岩质边坡滑动趋势Fig.9 The slide trend of the rock slope with single weak structural plane

可以看出，单层软弱结构面顺层岩质模型边坡在开挖和模拟降雨后，模型边坡在软弱结构面以上发生滑裂，随着降雨量不断增大，模型边坡滑动量逐渐增大。模型边坡从坡体内至坡体表面位移逐渐减大，从坡顶至坡脚位移也逐渐减大，表现为坡脚滑动牵引坡体滑动，说明该边坡属于牵引拉裂式破坏。

2.2 B组试验结果

2.2.1 SAA位移监测分析

SAA监测结果显示，模型边坡表面的X方向累计位移为7 mm，Y方向累计位移为4 mm；在软弱结构面处，X方向累计位移为4.5 mm，Y方向累计位移为4 mm。X方向位移在边坡表面为最大值，沿SAA竖直方向向坡体内部逐渐减小；Y方向位移从边坡表面到软弱结构面基本保持不变，沿SAA从软弱结构面至坡体内部逐渐减小。SAA边坡累计位移如图10所示。位移与时间关系如图11所示。

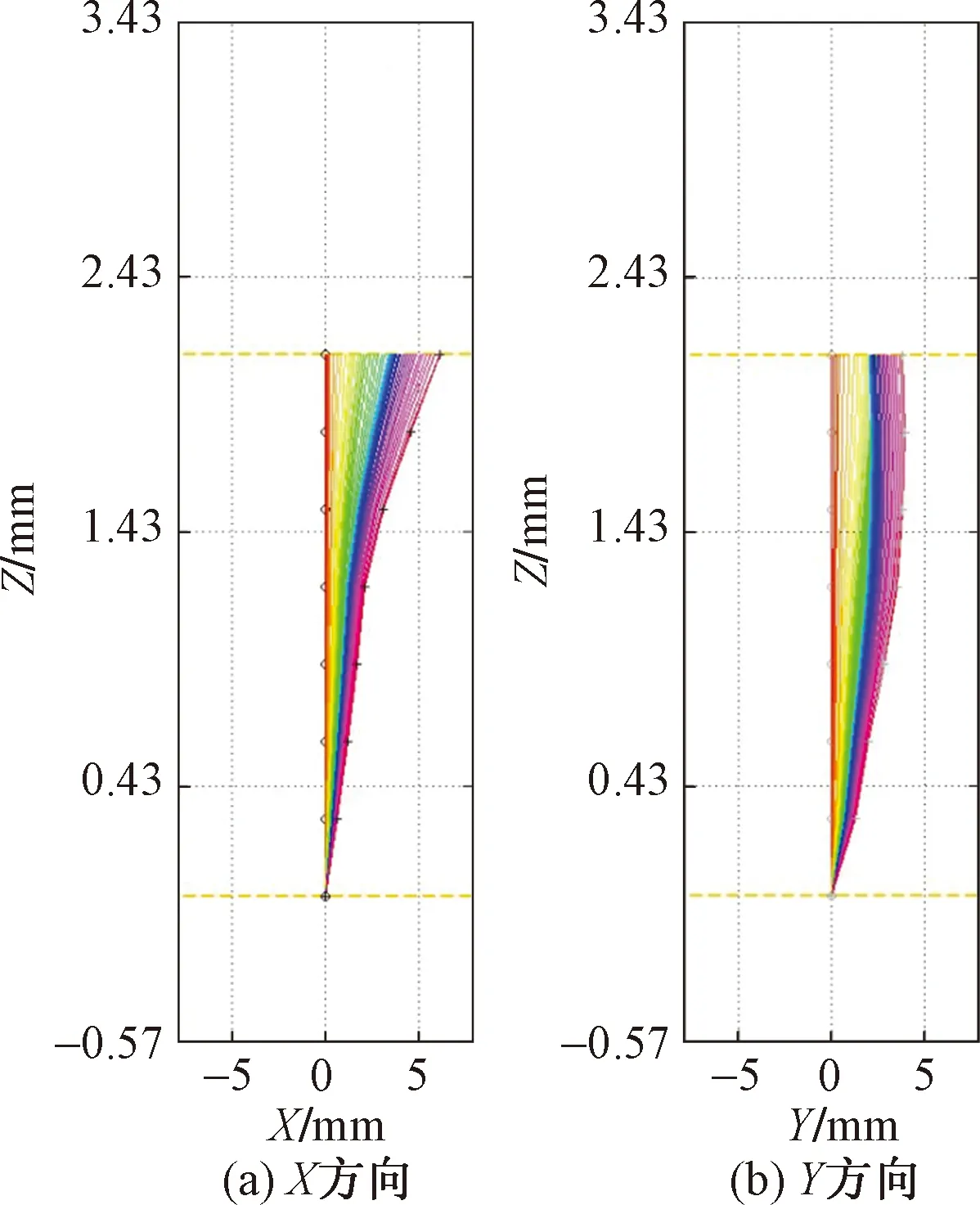
图10 SAA累计位移Fig.10 SAA cumulative displacement

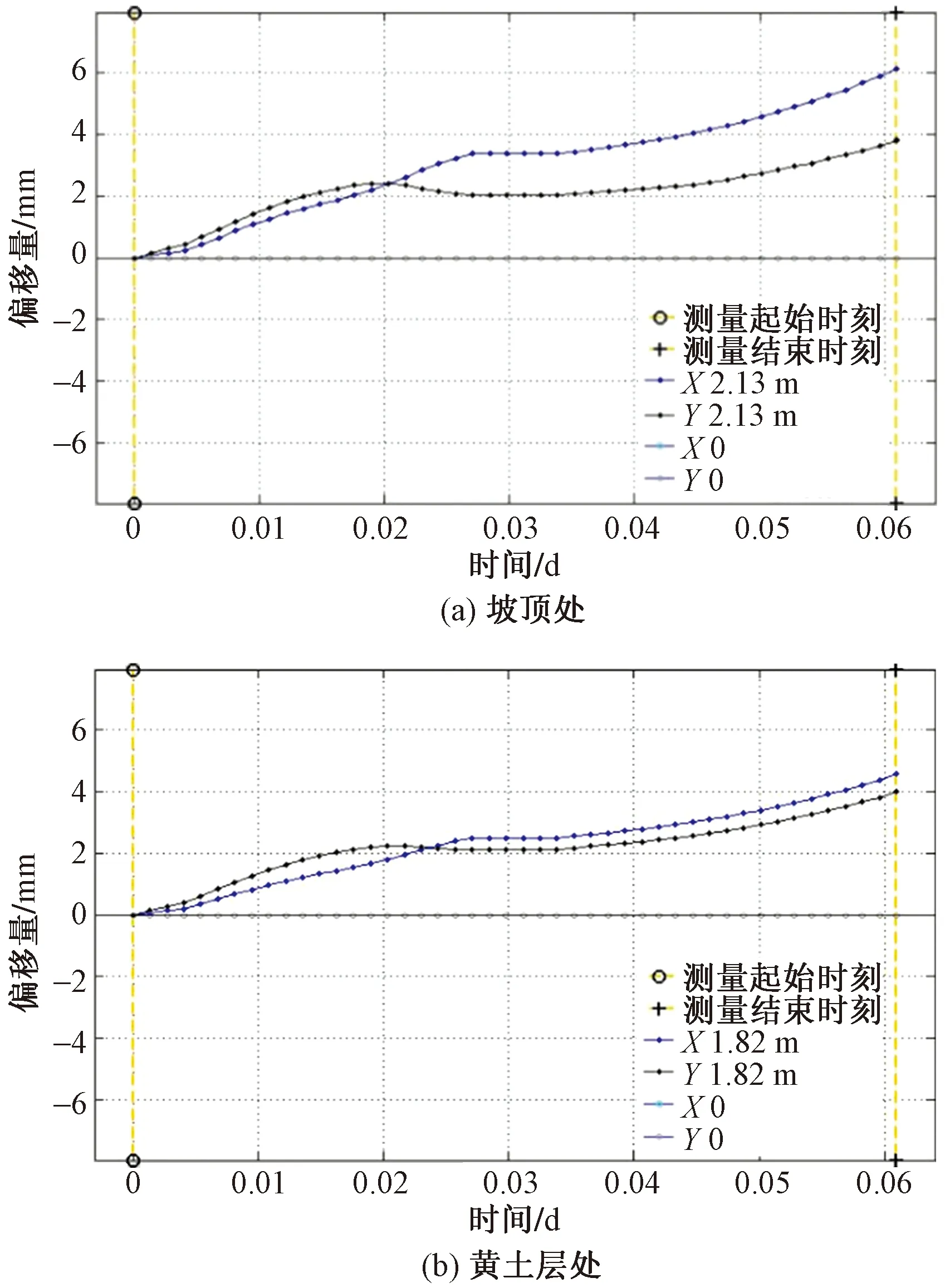
图11 SAA位移与时间关系Fig.11 Displacement versus time

2.2.2 三维激光扫描仪监测数据分析

三维激光扫描仪监测方法同A组，处理所得各状态下模型边坡沉降值如图12所示。边坡沉降图表明：模型边坡开挖后，在Y轴方向-0.5～-1 m处出现小范围滑塌现象，沉降量为0.05～0.1 m。随着降雨量逐渐增大，模型边坡沉降量也逐渐增大。模拟小雨状态下滑塌范围增大，为Y轴方向-0.5～-1.1 m处，同时沉降量增大至0.05～0.15 m；模拟大雨状态下，模型边坡出现大规模滑移现象，Y轴方向-1.5～-3 m处大量滑体发生滑塌，沉降值为0.2～0.3 m；同时坡顶处在卸荷作用下也发生少量滑塌。

2.2.3 人工摄影测量数据分析

用人工摄影测量数据作出边坡的位移矢量及趋势图，如图13所示。双层软弱结构面顺层岩质模型边坡在开挖和模拟降雨后，模型边坡发生大型滑坡，模型边坡沿软弱结构面中下部全部滑下，坡顶岩体在卸荷后稳定性也随之减小，发生小规模滑塌。对比图9与图13，含双层软弱结构面边坡较含单层软弱结构面边坡在相同工况下，滑动范围更大，滑动体积更大，造成的危害也就更大。同时观测结果显示，滑体多呈流塑态，前缘可见典型的鼓张裂隙，滑移时表现出流速高、流程长的特点。

3 数值模拟

3.1 模型建立

选取K23+921断面作为基础断面，根据选取部分的体积尺寸(730 m×225 m×30 m)，采用3DEC数值模拟软件建立了计算模型，如图14所示，划分网格时设置长度为15 m。边坡模型选取适当的控制点分成开挖岩土体、滑体、滑床3个部分，其中滑体与滑床本构模型采用基于弹塑性理论分析的摩尔-库仑模型，潜滑面采用库仑滑移模型。

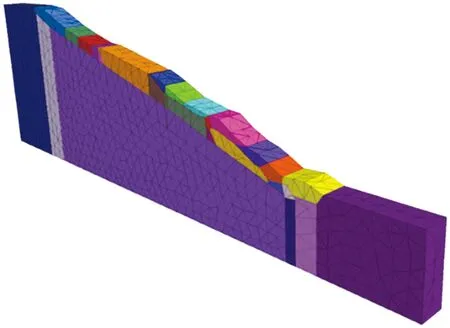
图14 边坡模型示意图Fig.14 Schematic diagram of slope model

3.2 边界条件与计算参数

计算模型的边界条件采用位移约束条件，X方向分别选取X=-100 m和X=630 m两个垂直界面；Y方向分别选取Y=0和Y=30 m两个垂直界面；模型底部选取Z=0水平边界；模型顶部则表面则设为自由面。综合参考各级岩质围岩基本物理力学参数和边坡勘察报告，得到本次模拟计算物理力学参数，如表4所示。

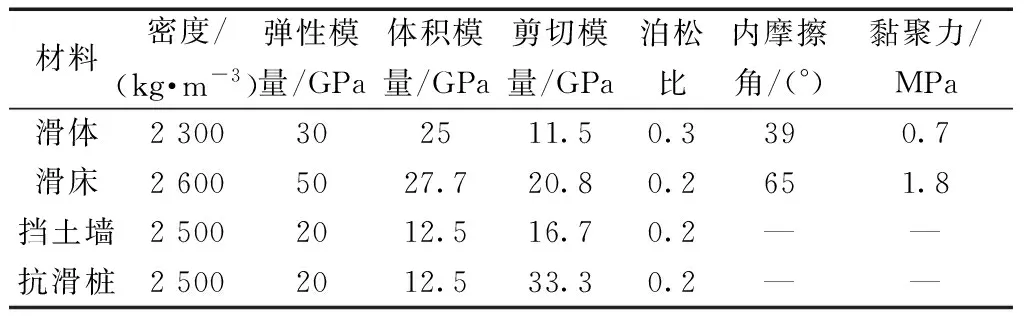
表4 模拟计算物理力学参数

3.3 计算结果分析

对原状、开挖后、挡墙支护和挡墙抗滑桩支护这4种不同工况条件下的边坡进行了模拟，在模拟过程中记录最大不平衡力和4个监测点的位移变化。最大不平衡力模拟监测结果如图15所示，位移与稳定性统计结果汇总如表5所示。

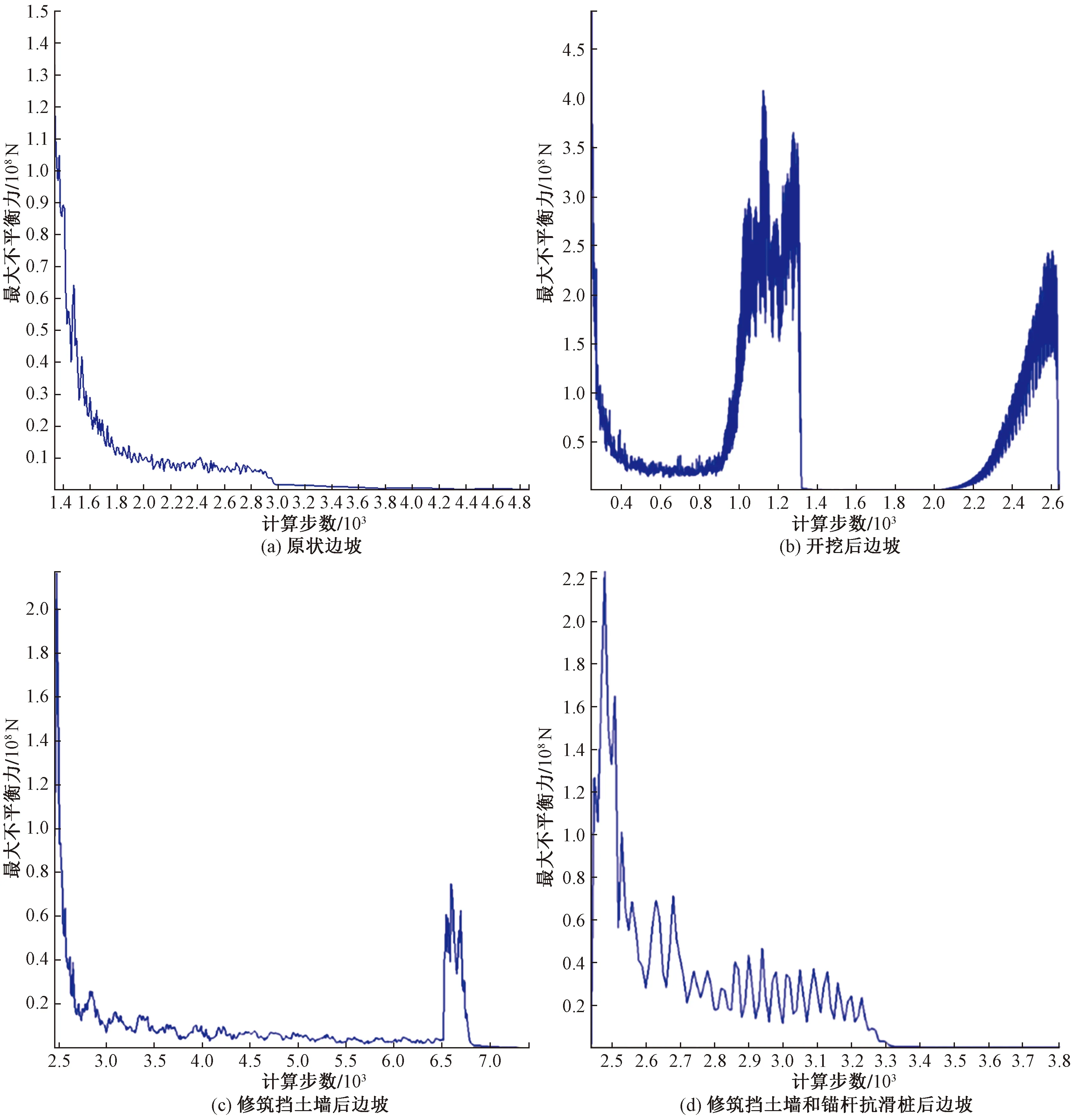
图15 最大不平衡力监测曲线Fig.15 Maximum unbalanced force monitoring graph

表5 不同工况下边坡的位移与稳定性

模拟分析可知，原状边坡的应力集中程度和变形均较小，坡肩处出现较小拉应力，但坡体可维持总体稳定。坡脚开挖后，坡体将无法继续维持稳定，滑体上开始出现较大的拉应力，直至破肩拉断，于是滑体开始整体下滑，坡肩处拉应力释放，应力集中点转移至二级滑体中部。由于坡脚一级滑体下滑规模明显大于二三级滑体，可判别为牵引式滑坡。这说明坡脚削方对坡体整体的稳定性影响较大，削坡后需要及时采取防护措施。

坡脚开挖后，为防止坡体发生进一步破坏，工程中采用了修筑挡土墙的防护手段。但据模型计算显示，挡土墙对减小坡体滑移量具有一定的积极作用，但单一采用挡土墙防护的坡体仍然难以保证稳定性，坡体发生整体变形的现象依旧存在，因此修筑挡土墙不能单独作为该边坡的抗滑措施。并且，在实际工程中，修筑挡土墙更多的是作为应急的坡体防护手段，以阻止坡体的快速变形，若要维持该边坡的长期稳定性，仍需要结合抗滑桩对坡体进行治理。

4 结论

通过对顺层岩质边坡破坏过程的模型试验和机理分析，以及数值模拟的验证，得到如下结论。

(1)含单层软弱结构面顺层岩质边坡的破坏以沿软弱结构面的多级牵引式滑动破坏为主。在开挖和降雨作用下，坡脚附近岩体因卸荷作用开始出现以横向拉张裂缝为主的小范围变形；软弱结构面强度随着雨水入渗逐渐减弱，以致上覆岩体沿结构面下滑，形成一级滑动，并同时沿横向裂缝发生拉裂。随着降雨入渗作用不断增大，坡体进一步发生多级滑动直至边坡完全破坏。

(2)含双层软弱结构面的顺层岩质边坡的破坏过程分为以下3个阶段：局部变形阶段，即开挖卸荷作用下坡脚处产生局部滑塌；蠕滑变形阶段，坡体上层软弱结构面上覆岩体随降雨入渗强度显著下降，并沿上层软弱结构面发生蠕滑变形，同时坡体表面发生出水现象，并伴有贯穿裂缝的出现；整体滑动破坏阶段，在降雨量不断加大的条件下，岩体强度显著降低并逐渐趋于流塑态，最后坡体沿着上层软弱结构面发生滑动破坏。

(3)软弱结构面对岩质边坡滑动破坏的作用主要有两方面：一方面表现为软弱结构面在雨水入渗作用下的进一步软化，最终发展形成坡体滑动破坏的滑带；另一方面，软弱结构面具有减弱雨水向下层岩体入渗的作用，在降雨量足够大的条件下，将导致上覆岩体迅速饱和，强度急剧降低，随即沿软弱结构面发生大规模的整体破坏。

(4)相较于开挖卸荷作用，强降雨的入渗作用是含软弱结构面顺层岩质边坡破坏的主要诱发因素和致灾因素，且含双层软弱结构面顺层岩质边坡的滑动破坏受雨水入渗的影响尤为明显。