基于改进突变模型的输气管道滑坡灾害失效可能性评价

2021-04-29王珀严继发尹航张萌

油气田地面工程 2021年4期

王珀严继发尹航张萌

1中油国际管道公司

2中国石油天然气集团公司青海油田分公司

目前，我国兴建了一批输气管道工程，如中缅天然气、中贵天然气、川气东送、西气东输、中亚天然气管道工程等，这些管道均具有大管径、高压力、高钢级的特点。管道沿线多处采用穿跨越方式，沿线水文地质情况复杂，很多区域内伴有坡面水毁、台田地水毁、坍塌、滑坡、泥石流等自然灾害[1]。据美国PHMSA 统计数据表明，因山体滑坡导致的事故约占自然灾害的54%，2015 年12 月西气东输二线广深支线因山体滑坡导致管道泄漏，造成73 人死亡，直接经济损失8.8 亿元。为避免滑坡灾害对输气管道的影响，在设计阶段通常采取避让方式，但由于各类原因有些管段必须从已有或潜在的滑坡区通过[2]，同时在建设和运行期间，因人为施工、地震、降雨等活动也会诱发形成新的滑坡，故滑坡灾害是一种不可回避的地质灾害[3]。因此，采用客观公正的方法对输气管道滑坡灾害进行风险评价显得尤为重要。

现阶段，滑坡灾害风险评价主要集中在失效概率预测和监测能力分析上。冼国栋等[4]以西南地区沿线滑坡灾害为样本，建立了危险性评价指标体系，并根据敏感性进行了指标筛选，但该方法只考虑了诱灾环境，未考虑管道自身或沿线敷设条件对滑坡的影响；刘迎春等[5]、钟威等[6]将滑坡灾害发生的可能性划分为地质灾害易发性和管道易损性两类，通过层次分析法对指标进行打分评价，但未考虑监测治理情况对安全运营的影响。因此，从孕灾诱灾因素、管体承灾属性和监测治理措施三方面入手，建立多层次滑坡风险评价体系，基于突变模型，采用改进的突变级数评价法对滑坡风险进行评价，识别导致灾害发生的主要原因，以期为该类管道完整性提供理论依据和实际参考。

1 原理和方法

1.1 突变原理

20 世纪60 年代，法国数学家THOM 创立了突变理论，该方法综合了拓扑学、奇点理论和结构稳定性等手段，对自然界中的突变行为进行了研究。突变级数评价法注重各指标之间的相对重要度，无需对评价指标进行权重赋值，避免了主观判断对评价结果的影响，在石油化工、水利水电、矿场普查等方面广泛应用。

通常采用势函数表征系统状态变量和控制变量的关系，反映系统的突变性质，假设势函数为f(x)，通过对势函数求一阶导数得到临界点集，对临界点集再求一阶导数得到奇点集，将临界点集和奇点集函数联立消除x得到分歧点方程，由分歧点方程可导出归一化公式。根据基本突变模型不超过5 个控制变量的要求选择突变模型，突变模型及归一化公式见表1。

表1 突变模型及归一化公式Tab.1 Catastrophic model and normalization formula

1.2 建模步骤

（1）构建评价指标体系，通过分析评价对象内部作用机理，将难以量化的评价对象逐级向下分解为底层指标。

（2）对评价指标进行无量纲处理，由于评价指标的单位和取值范围均不同，且有些指标为定性分析，需要将其转为[0，1]区间的数值，分别采用正向指标（取值越大越好）、反向指标（取值越小越好）和适度指标（取值接近某个值）进行计算，其中适度指标采用贡献率分析法。

正向指标：

反向指标：

式中：xj为原始数据；为无量纲化后的数据；xmin(j)和xmax(j)分别为隶属函数的边界值。

（3）将无量纲处理的评价指标代入归一化公式，计算得到各级评价指标的突变隶属函数值，当各控制变量之间不存在相互作用时，取各突变隶属函数值的最小值，如燕尾突变类型：x=min[xa，xb，xc]；当各控制变量之间存在相互作用时，取各突变隶属函数值的算术平均值，如燕尾突变类型：。

（4）通过分析各层控制变量的隶属函数值和评价体系总的隶属函数值，对应失效等级可能性区间，得到失效可能性等级，判断系统的突变情况。

1.3 改进的突变模型

由于归一化公式的聚焦特性会导致隶属函数值偏高，大部分函数值接近1 且间距过小，不利于对结果的分类判断。在此，对突变模型进行改进，根据评价指标体系，定义指标层的隶属度值均为xi，根据前文的建模步骤计算系统总的隶属函数值yi，采用Origin 对两者进行拟合，通过拟合公式将计算得到隶属函数值转为yi，同时失效可能性区间也相应调整。

1.4 贡献率法

贡献率法是计算研究区域内各种指标对滑坡发育的作用大小，比较各类指标对滑坡发育的贡献程度，可为滑坡危险性分析提供可靠依据。步骤如下：

（1）计算某指标在各评价区间内的面积贡献G1、数量贡献G2和规模贡献G3，公式为

式中：ai(s)、ai(n)、ai(υ)分别为某指标在各区间内的滑坡面积、数量和体积；S、N、V分别为某指标在所有区间内的滑坡面积、数量和体积。

（2）将公式（3）～（5）的计算结果从高到低排序并依次赋值，赋值范围5 到1，赋值间隔为1，采用求算术平均值的方法将G1、G2和G3在同一区间内的数值叠加，计算不同区间内的综合贡献指数G(ai)，公式为

式中：n为贡献类型数量，n=3；G(a)i为不同贡献类型的数值。

（3）计算得到某指标对滑坡发育的综合贡献率G0(ai)，公式为

式中：m为评价区间个数。

2 实例计算

中缅天然气管道起点位于缅甸西海岸皎漂地区，途经西海岸滨海低地、若开山区、伊江盆地、掸邦高原、缅北山区等地貌单元后由瑞丽进入中国，在中国穿越云南、贵州、广西、重庆等多个地区，全长1 100 km，设计压力为8～14.5 MPa，外壁采用3PE 防护层，全线采用密闭输送工艺。中国段管道经过横断山脉、无量山脉、喀斯特地貌等复杂地形，其中云贵地区地形变化大、坡高谷深、岩层破碎，属于高地震烈度、高地应力、高地热的“三高”活动区域，加之热带季风汛期带来强降雨甚至极端降雨，常导致滑坡、泥石流等自然灾害的发生。根据地质灾害评估资料，云贵段共有滑坡及不稳定斜坡195 处，泥石流25 处，坍塌18 处，其中滑坡灾害对管道安全运营的风险最大，在此以中缅天然气管道云贵部分管段为例进行管道风险评价。

2.1 构建指标体系

通过对已有滑坡灾害的事故统计和调研分析，输气管道主要受孕灾诱灾因素、管体承灾属性和监测治理措施三方面影响。孕灾诱灾因素是指诱发坡体发生滑坡的影响因素，不同地形地貌、地层岩石下发生滑坡的概率不同，即使同样环境因素条件下，受降水量和人类活动的影响，滑坡发生的概率也不同，因此将其细分为环境因素和诱发因素两种[7-8]；管体承灾属性是指可以承受的滑坡体施加应力的能力，主要与敷设情况及材料和运行情况有关；监测治理情况是指采用地表位移、GIS 等相关技术，测试管道应力应变的变化规律，判断管道安全运行状态，并通过排水保护、风化防护、抗滑加固等措施进行修复处理，可分为监测情况和治理情况两种。滑坡灾害失效可能性评价指标体系如图1所示，分为目标层、准则层、指标层，其中指标层共包含22 个指标。当滑坡灾害可能性较大时，可通过调整管体承载敏感性来降低滑坡造成的危害；对于已建成管道，孕灾诱灾因素和管体承灾属性均以固定，此时可通过对管道或坡体采取相应措施，以降低滑坡发生的可能性或提高管体承载属性[9-10]。此外，评价管段均为埋地敷设且埋深较浅（一般在2 m 左右），具有薄壳、线性和内含高压有毒介质等特点，决定了沿线地质灾害对管道危害的特殊性，即较小的地质灾害也会造成较大的后果。因此，灾害体与管体属性和监测治理措施遵循互补原则，各控制变量存在相互作用。用“+”号表示下一层指标遵循互补原则，用“-”号表示下一层指标不遵循互补原则。

图1 滑坡灾害失效可能性评价指标体系Fig.1 Evaluation index system of failure probability of landslide disaster

由图1 可知，评价指标存在定量和定性指标，定量指标依据实际数据进行等级划分，定性指标依据规范和相应标准进行等级划分，将失效可能性划分为低、较低、中、较高、高5 种，定性指标的分级判定准则见表2。其中滑坡宽度采用Workbench进行应力分析，根据有限元结果测算特定灾害点位置的最大Mises 应力.根据应力失效准则，当最大Mises 应力超过管道屈服强度时管道失效，在此定义滑坡宽度系数μ评价滑坡宽度稳定性，公式为

式中：L为实际滑坡宽度，m；Lmax为管道屈服强度对应的极限滑坡宽度，m。

2.2 确定拟合公式

由图1 构建的评价指标体系，在指标层隶属度值xi取值为0～1、步长0.05 时，计算系统总的隶属函数值yi分别为0、0.705 2、0.761 5、0.797 6、0.825 6、0.846 7、0.867 4、0.880 5、0.896 2、0.901 4、0.918 8、0.929 5、0.936 2、0.948 5、0.957 1、0.965 9、0.970 1、0.980 6、0.9896、0.993 7、1，用Origin 进行拟合，如图2 所示，两者呈幂函数，相关系数R=0.999 1，函数关系为

表2 定性指标分级判定准则Tab.2 Classification criteria for qualitative indicators

图2 指标层隶属度值与系统隶属度值的关系Fig.2 Relationship between the membership value of the index layer and the membership value of the system

2.3 数据无量纲处理与归一化计算

对C3、C8、C9、C13、C14、C15、C16 采用正向指标计算；C2、C6 采用反向指标计算；C4、C5采用适度指标贡献率计算；C1、C7、C10、C11、C12、C17、C18、C19、C20、C21、C22 为定性指标，采用人为赋值方法，对应失效可能性等级的分值分别为0、0.125、0.375、0.625、0.875、1。对于定量指标，C2、C3、C4、C5、C6、C8、C9 结合国家测绘局提供的DEM、DRE 基础数据和Arcgis 软件获得，C13～C16 根据管道投产、运行、维抢修等长期监测数据获得，得到滑坡在各评价区间的综合贡献率，按照极差转换法将最大综合贡献率转为1（表3）。分别对QAF205-QAF209 号桩范家寨滑坡（1 号滑坡）、QAF197-QAF199 号桩江家山不稳定滑坡（2 号滑坡）、QAF200-QAF201 号桩烂包头滑坡（3 号滑坡）、QAE104-QAE105 号桩老白坟不稳定斜坡（4 号滑坡）、QAF200-QAF202 号桩马家山滑坡（5 号滑坡）、QAF101-QAF104 号桩漂亮河滑坡（6 号滑坡）、QAF202-QAF204 号桩秦家屋滑坡（7 号滑坡）、QAF198-QAF200 号桩高山滑坡（8 号滑坡）、QAF162-QAF163 号桩沙子镇滑坡（9 号滑坡）等9 个滑坡的指标进行无量纲化处理（表4）。

表3 适度指标区间综合贡献率Tab.3 Comprehensive contribution rate of moderate index interval

根据表1 结果，采用归一化公式逐级向上进行量化递归计算，以1 号滑坡为例，孕灾诱灾因素中的环境因素有C1、C2、C3、C4、C5 等5 个指标，属棚屋突变且遵循互补原则。

孕灾诱灾因素中的诱发因素有C6、C7、C8、C9、C10 等5 个指标，属棚屋突变且遵循互补原则。

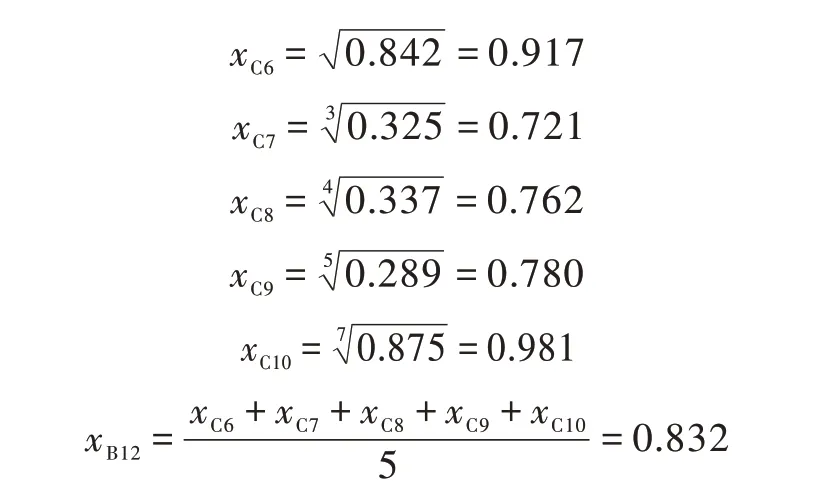
逐层向上，孕灾诱灾因素属尖点突变且遵循非互补原则。

表4 指标层数据无量纲处理结果Tab.4 Dimensionless processing results of index layer data

表5 1 号滑坡突变隶属函数值Tab.5 Catastrophic membership function values of No.1 landslide

同理，求出评价指标体系中剩余部分的突变隶属函数值（表5），系统总的隶属函数值为0.872，根据公式（10）转换后得0.354。

依照上述步骤对其余8 个滑坡的总隶属函数值进行计算，根据公式（10）进行转换，改进前后的滑坡分级判定准则见表6，计算结果见表7。

表6 改进前后滑坡判定准则Tab.6 Judgment criteria for landslide before and after improvement

表7 滑坡评价计算结果Tab.7 Calculation results of landslide evaluation

由表7 可知，对比前后计算结果，改进前隶属函数值较大且贴近1，难以区分评价结果的优劣，改进后隶属函数值均匀分布在[0，1]区间，且未造成信息失真，数据分辨率更高。以1 号滑坡为例，孕灾诱灾因素、管体承灾属性和监测治理措施隶属函数值对应的失效可能性等级分别为低、较低、中，总的隶属函数值对应的失效可能性等级为较低，可见1 号滑坡中监测治理措施是影响管道失效的主要因素。根据有限元分析，1 号滑坡的最大Mises 应力为258.7 MPa，X70 管线钢最小屈服强度为485 MPa，说明该处管道暂时不会超过屈服应力而断裂，可在管道中心及滑动与非滑动的过渡区域设置应力监测和位移装置掌握管道变化，进行实时预警。

9 处滑坡中2 号、3 号较高风险滑坡隶属函数值位于较高等级上限，说明当某些指标发生变化时，容易从较高风险转为高风险，应重点关注；5 号、7 号、8 号、9 号滑坡虽然目前处于中等风险，但隶属函数值在较低风险与中等风险之间，可采取正确的治理措施，如清除滑坡体，完善灾害影响区域内的排水措施，截流地表和地下水流，将水体引出坡体范围，对斜坡采取减压反重措施，对坡脚加抗滑桩，对坡体采用锚固等方式，降低风险区间，提升滑坡稳定性。仅有1 处现场勘察结果与评价结果不相符，但9 处滑坡的失效可能性总体趋势与实际勘察结果相符。