带杆件弯曲的网壳结构稳定极限承载分析

裴云亮柳锋任参邴卿德

(1.山东建筑大学 土木工程学院，山东 济南250101；2.山东建大建筑规划设计研究院，山东 济南250000)

0 引言

网壳结构属于缺陷敏感型结构，初始缺陷对其稳定极限承载力的影响较复杂。 初始缺陷可分为整体缺陷和杆件缺陷，其中整体缺陷主要指节点位置偏差，而杆件缺陷包括杆件初弯曲、内力初偏心以及残余应力等。 MORRIS[1]发现初始几何缺陷可使结构的临界荷载下降35%，稳定分析中需考虑缺陷的影响；对于考虑节点偏差和不考虑节点偏差的结构，杆件初弯曲将明显降低结构承载力，并且能够改变结构的塑性发展程度[2-3]；与仅考虑结构整体初始几何缺陷的计算结果相比，杆件初弯曲会进一步降低结构的稳定承载力，且当杆件初弯曲幅值较大时，杆件初弯曲对结构稳定承载力的影响不容忽视[4]；马腾飞等[5]在考虑节点缺陷和杆件缺陷的基础上，通过削减不同位置处的杆件截面，使被削减的杆件在网壳结构整体失稳之前屈曲，不同位置处的杆件屈曲会不同程度的降低网壳结构稳定极限承载力；赵阳等[6]和田伟等[7-8]对网壳结构整体稳定分析时发现，结构整体失稳之前存在杆件失稳的网壳结构，有必要引入杆件缺陷，考虑其对杆件失稳的影响，若不考虑杆件失稳会过高估计结构的承载能力，局部构件的失稳退出并不会导致结构整体承载力的突然丧失，结构仍会继续承载。

为了不影响结构的安全和正常使用，规范对上述缺陷限值是有明确规定的。 在实际的大跨网壳结构中不可避免的存在杆件几何缺陷，文章以某大跨度网壳结构实际工程为研究对象，基于对结构中弯曲杆件的实测数据，研究几何缺陷对实际网壳结构稳定承载性能的影响。

1 实际大跨网壳结构现场检测和设计复核

某网壳结构是一个跨度为151.8 m、矢高为45 m的双层球面网壳，此网壳共有10 302 根杆件，杆件材料为Q235B 钢，共有2 647 个节点，节点采用的是螺栓球节点，网壳结构如图1 所示。 在使用过程中，发现该网壳结构存在部分弯曲的杆件，如图2所示。 为了解杆件弯曲对网壳结构性能的影响，对此网壳结构进行了现场检测和设计复核工作。

图1 网壳结构图

图2 杆件弯曲图

1.1 杆件尺寸与变形检测

采用三维激光扫描仪、游标卡尺等测量工具对网壳进行检测。 网壳结构共有11 种杆件规格，分别为Φ75.5×3.75、Φ88.5×4、Φ114×4、Φ140×4、Φ159×6、Φ159×8、Φ159×10、Φ180×10、Φ180×12、Φ219×10、Φ219×12，杆件的几何尺寸、截面规格与设计图纸相符，尺寸偏差满足要求[9]。 在对网壳结构变形检测时，发现其中有16 根杆件产生挠曲变形，这16 根杆件实际分布位置如图3 所示，杆件各参数见表1。

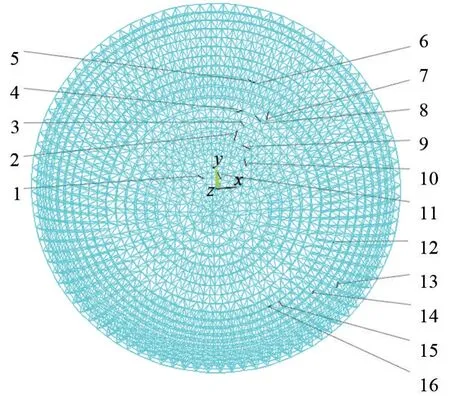
图3 弯曲杆件位置示意图

表1 弯曲杆件参数表

1.2 设计复核

采用3d3s 钢结构设计软件设计复核了网壳结构，此结构在建模时支座采用固定铰支座。 对结构进行弹性静力分析和弹性全过程稳定分析，网壳结构荷载取值如下:网壳上、下弦永久荷载分别为0.5 和0.1 kN/m2；活荷载、风荷载和雪荷载均为0.5 kN/m2；温度荷载为±40 ℃；地震荷载为地震设防烈度7 度(0.15g)，主要荷载组合为:(1) 恒荷载＋活荷载；(2) 1.20 恒荷载＋1.40 活荷载；(3) 1.35 恒荷载＋140×0.70 活荷载；(4) 1.20 恒荷载＋140×0.50活荷载＋1.30 水平地震；(5) 1.20 恒荷载＋1.40 风荷载；(6) 1.20 恒荷载＋1.40 活荷载＋1.40×0.60 风荷载；(7) 1.20 恒荷载＋1.40×0.70 活荷载＋1.40 风荷载；(8) 1.20 恒荷载＋1.40 活荷载＋1.40×0.60 温度荷载。

对设计结构在上述8 种荷载组合下分别进行计算，复核结果如下:杆件最大强度应力比为0.89，最大稳定应力比为0.98，结构最大挠跨比为1/1 494，整体稳定系数为24，因此网壳结构在设计荷载作用下，杆件最大应力比、结构最大挠跨比以及安全系数均满足要求[10]，结构具有良好的设计承载力，杆件出现弯曲变形不是因为设计承载力不足引起的。 为探讨弯曲的杆件对大跨网壳结构稳定极限承载能力的影响，对网壳结构进行稳定极限承载分析。

2 缺陷模态的确定

目前，在钢结构整体稳定分析中主要考虑结构几何缺陷的影响，选用缺陷模态法引入初始几何缺陷，主要有随机缺陷模态法和一致缺陷模态法两种方法[11]。 随机缺陷模态法能够较好的反映结构的实际工作性能，但计算量大，不适合网壳结构非线性分析；一致缺陷模态法概念清晰、计算简便，认为缺陷模态是结构失稳时的位移倾向，有利于了解结构的整体稳定性，因此选用一致缺陷模态法确定结构的几何缺陷分布。

2.1 杆件缺陷

假定上述16 根弯曲杆件的形状为正弦半波曲线，由式(1)表示为

式中l为杆件长度，mm；δ为弯曲幅值，其值取杆件弯曲实测值，弯曲方向为实测方向。

正弦半波曲线是一种理想化的简单弯曲形状，采用多段梁法模拟杆件弯曲[7-8，12]，其余钢杆件按理想直杆模拟。

在有限元分析中，杆件的划分段数会影响到计算结果的精确性，文献[4，7，13]是通过考察单杆有限元分析模型来确定划分段数，由于杆件与结构之间的刚度相互影响，为了更加符合结构真实受力状态，将弯曲杆件划分单元后引入到整体结构中进行线性屈曲分析，并通过比较邻近特征值变化的大小来确定杆件合理的划分段数。 将分析模型中弯曲的杆件分别划分为1、2、4、6、8、10、12 段，各模型在第1 阶屈曲模态的特征值如图4 所示。 随着杆件划分单元数量的增加，在第1 阶屈曲模态中，特征值越来越接近，当单元数量＞8 个时，特征值相差不大，考虑到杆件划分的单元越多结构计算量越大，因此在分析结构时对杆件采用8 单元的划分。

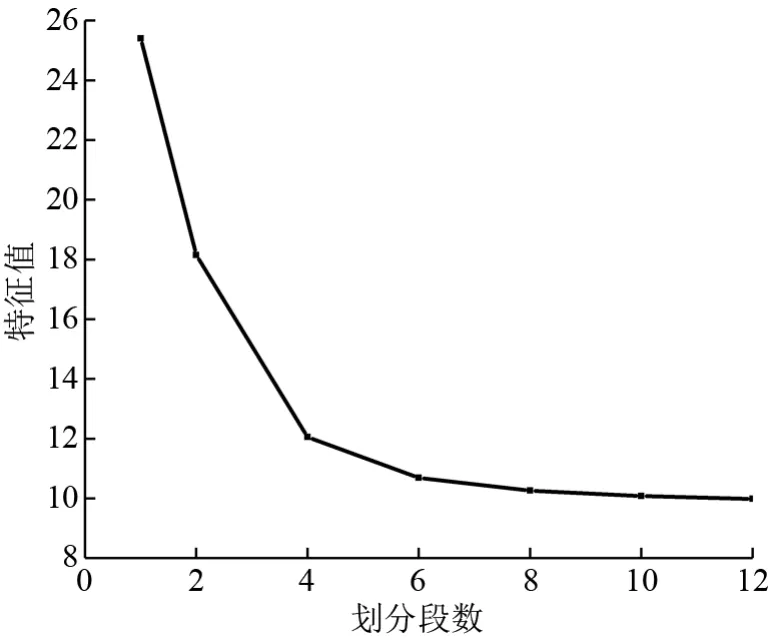
图4 第1 阶屈曲模态特征值图

2.2 整体缺陷

对网壳全过程分析时，初始几何缺陷分布可采用无缺陷结构的最低阶屈曲模态[10]，但由于特征值屈曲分析是线性分析，刚度矩阵是建立在结构未受载时的初始结构上，因而求得的最低阶屈曲模态不一定反映结构在整个非线性分析过程中的变形趋势[14]，尤其考虑到杆件弯曲的影响，这就可能不是结构最不利的初始缺陷分布形式；文献[15]提到大跨空间结构在失稳前可能已经产生很强的几何非线性甚至材料非线性，导致结构在发生整体失稳时的变形模态已不同于第1 阶线性屈曲模态。 因此将特征值屈曲分析得到的多阶屈曲模态分别作为缺陷分布形式引入模型中进行几何非线性分析，通过比较极限承载力系数(结构稳定极限承载力与荷载标准值的比值)大小确定最不利的整体缺陷。

2.3 最不利缺陷模态

将带有弯曲的杆件引入到模型中，对网壳结构进行线性屈曲分析，由于屈曲模态是网壳结构失稳时的位移倾向，对于跨度较大且形式复杂的网壳结构来说，高阶屈曲模态的影响不可忽略，选取网壳前30 阶屈曲模态作为初始几何缺陷分布，缺陷幅值取网壳实测挠度的最大值，通过修正初始网壳模型的节点坐标，形成30 个模型样本，然后分别对这30 个模型进行几何非线性分析，并通过比较极限承载力系数的大小，确定最不利的缺陷模态。 经计算得出第23 阶屈曲模态作为初始几何缺陷分布时对应的极限承载力系数最小，所以第23 阶屈曲模态是最不利的缺陷模态，如图5 所示，网壳结构发生局部凹陷现象。

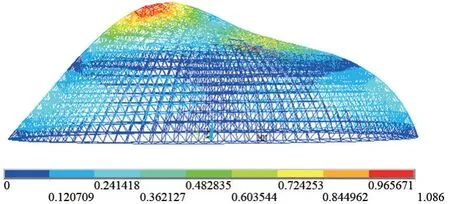
图5 最不利缺陷模态图/m

3 带杆件弯曲的网壳结构稳定极限承载分析

为了研究杆件弯曲对网壳结构稳定极限承载力的影响，分别建立以下3 种网壳分析模型:模型1 不考虑任何初始几何缺陷；模型2 将结构第1 阶屈曲模态作为整体初始几何缺陷，缺陷幅值取L/300(L为网壳跨度)；模型3 考虑弯曲杆件，采用最不利缺陷模态建立模型。

3.1 稳定极限承载力

采用有限元软件ANSYS，建立网壳有限元模型，杆件选用空间梁单元beam188，材料为Q235B钢，其本构关系采用理想弹塑性模型，分别对3 种模型进行几何、材料双重非线性分析，图6 给出了这3 种模型的极限承载力系数—竖向位移曲线，极限承载力系数和相应竖向位移见表2。

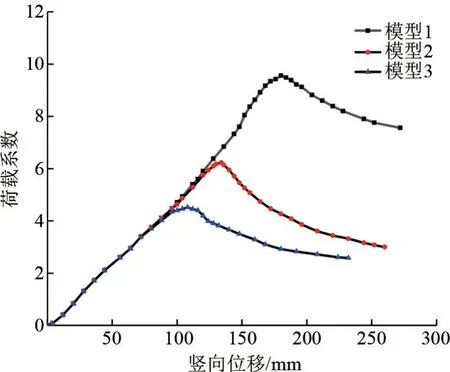
图6 极限承载力系数—竖向位移曲线图

表2 各模型极限荷载表

模型2 考虑整体缺陷，相比于模型1，其稳定极限承载力下降了34.1%；模型3 考虑杆件弯曲缺陷与整体缺陷，相比于模型2，其稳定极限承载力又下降了28.4%，可见杆件弯曲缺陷与整体缺陷对网壳结构稳定极限承载力影响较大。

3.2 失稳机理

为研究弯曲杆件对网壳结构失稳过程的影响，对模型3 在加载过程中发生失稳的杆件进行路径跟踪，确定杆件失稳的顺序及杆件轴力的变化，探讨网壳结构的失稳机理。 杆件失稳顺序及杆件失稳时的荷载值见表3，轴力负号表示杆件受压[16]。

在加载初期，网壳杆件的轴力和节点位移均随荷载的增加呈线性增长，当极限承载力系数增加到4.20 时，15 号杆件发生失稳，同时观察到15 号相邻两根杆件极限承载力系数—轴力曲线的斜率发生了变化，可见15 号杆件失稳后，向其相邻杆件卸载，结构内力重分布，由图6 可知，此时网壳结构的极限承载力系数—竖向位移曲线处于上升阶段，结构仍能继续承载。 15 号失稳杆件以及相邻杆件的极限承载力系数—轴力关系曲线和局部放大图如图7所示。

表3 失稳杆件及失稳时荷载与内力表

图7 15 号失稳杆件的轴力变化及放大图

当极限承载力系数增加到4.31 时，7 和9 号两根杆件同时失稳，此时7 和9 号相邻杆件极限承载力系数—轴力曲线的斜率发生了变化，可见两个杆件失稳后，向其相邻杆件卸载，结构内力重分布。 由图6 可知，此时网壳结构的极限承载力系数—竖向位移曲线处于上升阶段，结构仍能继续承载。 7 和9号失稳杆件以及相邻杆件的极限承载力系数—轴力关系曲线如图8 所示。

图8 7 和9 号失稳杆件的轴力变化及放大图

当极限承载力系数增加到4.42 时，2 号杆件发生失稳，同时观察到其相邻两根杆件极限承载力系数—轴力曲线的斜率发生了变化，可见2 号杆件失稳后，向其相邻杆件卸载，结构内力重分布。 由图6可知，此时网壳结构的极限承载力系数—竖向位移曲线处于上升阶段，结构仍能继续承载。 2 号失稳杆件以及相邻杆件的极限承载力系数—轴力关系曲线和局部放大图如图9 所示。

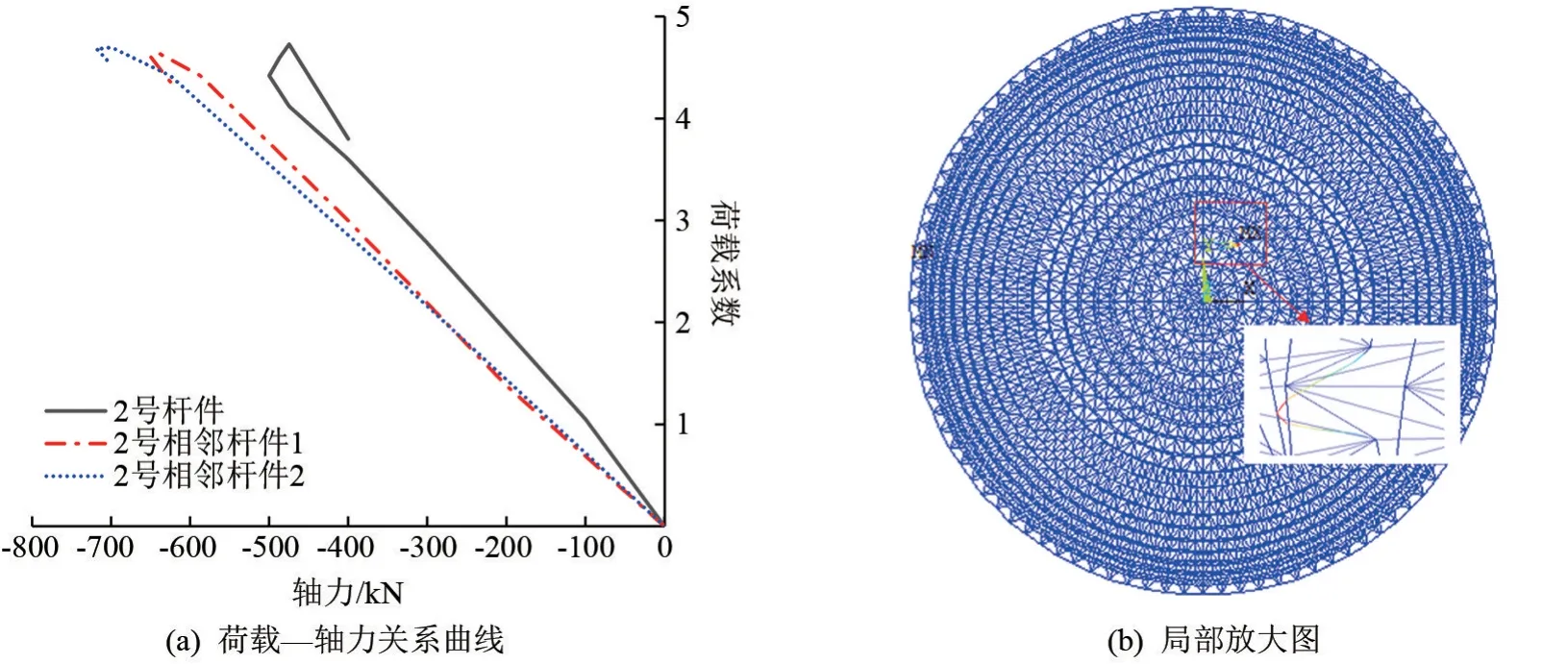
图9 2 号失稳杆件的轴力变化及放大图

当极限承载力系数增加到4.51 时，11 号杆件发生失稳，同时观察到其相邻两根杆件极限承载力系数—轴力曲线的斜率发生了变化，可见11 号杆件失稳后，向其相邻杆件卸载，结构内力重分布。 由图6可知，此时网壳结构的极限承载力系数—竖向位移曲线处于上升阶段，结构仍能继续承载。 11 号失稳杆件以及相邻杆件的极限承载力系数—轴力关系曲线和局部放大图如图10 所示。

图10 11 号失稳杆件的轴力变化及放大图

当极限承载力系数增加到4.59 时，8 和10 号两根杆件同时发生失稳，同时观察到其相邻杆件极限承载力系数—轴力曲线的斜率发生了变化，其轴力不再随荷载线性增加，可见两杆件失稳后，向其相邻杆件卸载，结构内力重分布。 由图6 可知，此时网壳结构的极限承载力系数—竖向位移曲线处于上升阶段，结构仍能继续承载。 8 和10 号失稳杆件以及相邻杆件的极限承载力系数—轴力关系曲线和局部放大图如图11 所示。

当极限承载力系数增加到4.73 时，网壳节点位移较大，结构整体出现偏移，发生整体失稳破坏，各杆件的轴力均随着荷载的卸载而减小，如图12所示。

由上述分析可知，网壳结构的最终破坏源于带有弯曲杆件的率先失稳，杆件的失稳使结构发生内力重分布，结构不会突然丧失承载力，仍能继续承载，随着荷载的增加，失稳杆件数量的增多，最终导致结构整体失稳。

图11 8 和10 号失稳杆件的轴力变化及放大图

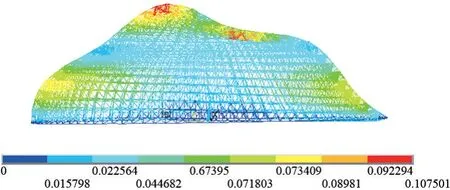
图12 网壳结构达到极限承载时的变形图/m

4 结论

通过对带有弯曲杆件的网壳结构进行几何、材料双重非线性承载力分析，得出以下主要结论:

(1) 网壳结构的最终破坏源于带有弯曲杆件的率先失稳，杆件失稳后向其相邻杆件卸载，致使结构内力发生重分布，结构不会突然丧失整体承载力而是继续承载。

(2) 网壳结构考虑了杆件弯曲缺陷与整体缺陷，较仅考虑整体缺陷时的承载力下降了28.4%，杆件弯曲缺陷对网壳结构稳定极限承载力的影响较大。