基于多轴载荷的汽车控制臂疲劳载荷块编制

2021-04-29胡浩炬邓小强余家皓郭绍良罗欢

汽车零部件 2021年4期

胡浩炬，邓小强，余家皓，郭绍良，罗欢

(广州汽车集团股份有限公司汽车工程研究院，广东广州 511434)

0 引言

汽车的耐久性是影响汽车产品竞争力的主要因素之一，因此耐久性试验是汽车产品开发的重要环节[1]。通常汽车的耐久性设计与开发需要经大量的实物台架试验验证，以底盘悬架零件为例，一般包含整车级、系统级、零部件级的耐久性试验[2]。零部件级台架耐久性试验一般为加速试验，整车路试采集的路谱信号通常很难直接应用于零部件级的结构疲劳试验。通过损伤等效方法获得等效于路试损伤的载荷块，再用于零部件台架耐久性试验，是目前国内外汽车厂商广泛应用的一种台架试验方法[3]。利用此方法，在保证产品质量的同时又可以缩短台架验证周期。但目前为止国内的大多数整车企业缺乏有效的技术手段定义零部件级的台架疲劳载荷，且在制定零部件级台架耐久性试验时大都只考虑单一方向的载荷，忽略了零件载荷的多轴性，适用性与可靠性通常不理想。如何制定合适的零件台架耐久性试验载荷以确保零件设计的可靠性，已显得尤为重要。

本文作者以某车型控制臂为研究对象，对其试验场路谱载荷进行单轴和多轴雨流分析、伪损伤计算、单轴与多轴载荷块编制，同时建立控制臂有限元模型，进行疲劳计算及对比分析，在结合控制臂路试应变采集数据，验证了基于多轴载编制的疲劳试验载荷块的有效性。

1 控制臂载荷谱与分析

1.1 载荷获取

图1为控制臂结构及试验应变采集位置。

图1 控制臂结构及试验应变采集位置示意

文中涉及的某车型控制臂结构为前麦弗逊悬架下控制臂，包含连接点：(1)与转向节连接的球铰点；(2)两个与副车架连接衬套点。根据控制臂的受载情况，通常其台架试验为约束与副车架连接的两个衬套点，球铰点作为加载点。

根据整车耐久性开发需求，底盘零部件应满足整车试验场道路耐久性试验。试验场道路包含路面见表1，经表中各路面不同循环次数组合，再与目标用户里程进行关联，得到试验场耐久循环，用于整车开发耐久性与可靠性验证[4]。

试验采集了该车型试验场道路的轮心六分力信号及控制臂两个位置的应变信号，应变信号采集位置如图1所示，部分典型工况应变信号采集结果如图2所示。以采集的轮心六分力作为输入经多体动力学载荷分解得到控制臂球铰点的试验场一个大循环的疲劳载荷如图3所示。方法中的车辆动力学模型已经过在车型开发中得到验证，载荷精度已获得验证，可满足车辆开发需求。

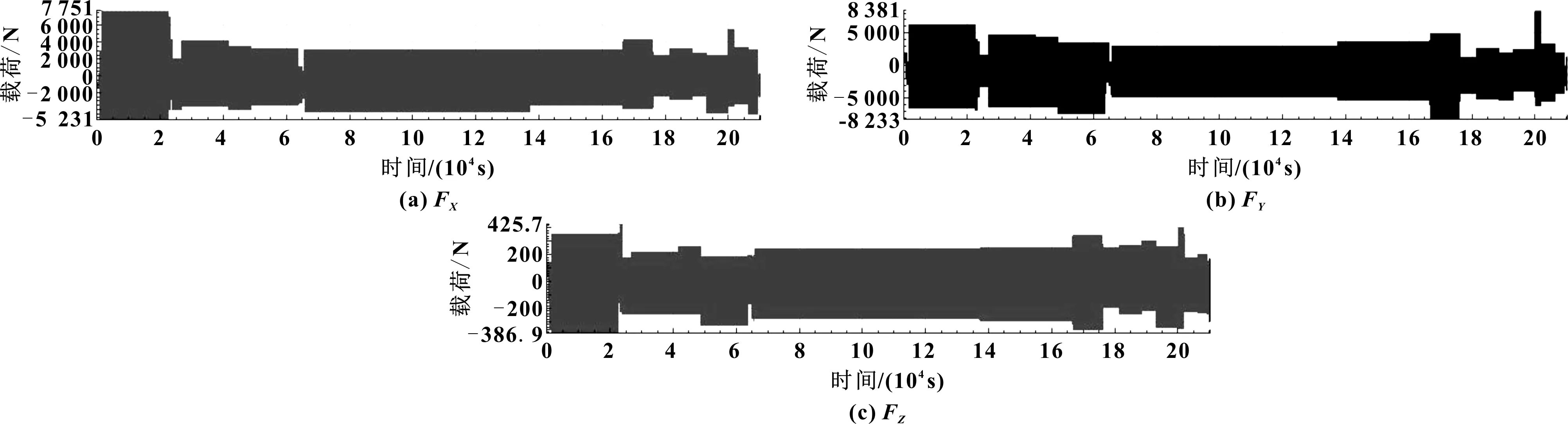
图3 控制臂球铰处的试验场道路谱载荷

1.2 幅值统计与伪损伤计算

控制臂球铰点处的载荷如图3所示，包含X、Y、Z3个方向的多轴随机载荷，X、Y、Z3个方向的载荷信息见表2。从表2可知球铰点处Z向载荷幅值较小，约为X与Y方向幅值的5%。

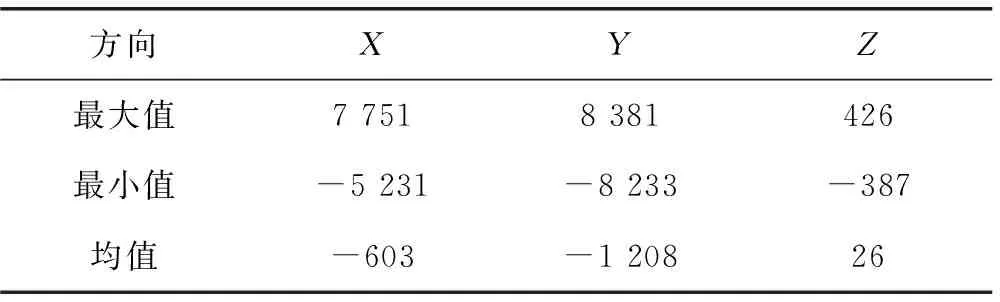
表2 控制臂球铰点载荷信息 N

伪损伤是指通过载荷直接计算疲劳损伤，其计算理论基础是基于局部应力-应变法[3,5]：通过选择进行相应的材料S-N曲线进行载荷谱的损伤统计得到控制臂球铰点的X、Y、Z各方向的伪损伤值如表3所示。

表3 控制臂球铰点三方向的伪损伤值

对比控制臂球铰点处三向载荷伪损伤值发现：Y向损伤值最大，X向次之，Z向非常小，可认为球铰处Z向载荷几乎不会对零件产生疲劳损伤。故控制臂台架耐久性试验可省去Z向载荷，只考虑X和Y方向载荷。另文中研究涉及的载荷块编制暂不考虑小载荷对疲劳结果的强化作用影响[6-8]。

1.3 载荷多轴性分析

为研究控制臂球铰点载荷的多轴性，文中采用LMS-Tecware软件提供的多轴雨流投影方法分析控制臂球铰点载荷的损伤分布，通过损伤分布情况来表征其载荷的多轴情况，其方法[9-11]如下：

假设一多轴载荷Lk(t)，将Lk(t)投影至β方向得到Lβ(t)：

(1)

选取所有可能的投影方向，基于上式将Lk(t)转换为Lβ(t)，再通过雨流计数和伪损伤计算得到各个β向的Lβ(t)的雨流计数统计与伪损伤值。β方向的选取可根据载荷Lk(t)的维数d进行确定，如d=2，β值见表4。

表4 β方向选取与转换比

因控制臂球铰处Z向载荷较小可省去，故选取X与Y载荷通过LMS-Tecware软件进行多轴雨流投影分析，得到球铰点测试载荷Lk(t)的X与Y组合的12个方向的伪损伤值与雨流计数结果，如图4所示。

图4 多轴雨流投影结果(X与Y组合的12个方向伪损伤分布)

由图可知，疲劳损伤最大的方向为(-0.50，0.87)，伪损伤值为17.66;疲劳损伤最小的方向为(0.87，0.50)，伪损值为1.27。

2 载荷块编制

2.1 单向载荷块编制

文中提到的单向载荷编制是不考虑X与Y两个方向载荷耦合，分别对X和Y方向的载荷进行载荷块制定。载荷块程序谱幅值一般分为3～8级，由德国工程师GASSNER于1938年首次提出，并得到广泛应用。各级载荷大小的划分按照幅值比系数法，幅值比系数分别取为：1，0.95，0.85，0.725，0.575，0.425，0.275，0.125[12]。基于此方法进行载荷谱分级，根据第2.1节中X与Y方向的单轴雨流统计结果，分别得到X和Y单轴方向的8级载荷谱见表5。

表5 单轴载荷分级结果

零件台架试验通常为加速试验，实际物理台架试验时会将8级载荷谱简化成1～3级载荷谱。

2.2 多轴载荷块制定

(2)

图5 零件受载图示

根据控制球铰点载荷分析可知，此车型控制臂Z向疲劳损伤非常小，其受载可视为X与Y两轴组成的随机载荷Lk(t)，故其等效的两轴载荷Leqk(t)可表示为

(3)

式中：Leq1、Leq2分别为X和Y方向的正弦载荷;A1、A2分别为X和Y方向正弦载荷的幅值;θ为Leq1与Leq2的相位差;N0为总循环次数;A1、A2、θ为未知量;0≤t≤N0。

若规定试验总循环次数N0为1×105次，依据上述方法求得Leqk(t)其X和Y两个输入方向的一级载荷Leq1、Leq2，其中A1=3 385.6 N，A2=4 140.3 N，θ=111.6°，载荷块结果见表6。测试载荷Lk(t)与等效载荷Leqk(t)的多轴雨流投影对比结果如图6所示。从图6可以看出等效载荷12个投影方向的伪损伤值与原测试载荷基本一致，且各方向的伪损伤值相差较小，损伤较大的几个方向的误差值在5%以内，说明等效载荷Leqk(t)与原载荷Lk(t)的多轴性基本一致。

表6 多轴载荷块

图6 控制臂载荷Lk(t)与等效载荷Leqk(t)雨流投影对比

3 疲劳计算与试验对比

3.1 有限元模型建立及标定

根据三维数建立控制臂有限元模型：控制臂金属钣金及焊缝采用壳单元模拟，控制臂球坐实体件采用四面体网格处理，衬套采用衬套单元处理，衬套刚度为实测值，整个控制臂有限元模型共计36 946个单元及48 625个节点。

有限元模型标定，通过已采集的前进制动、倒车制动、冲坑3个典型工况的应变采集数据进行有限元模型计算标定。典型工况应力计算结果图如图7所示。

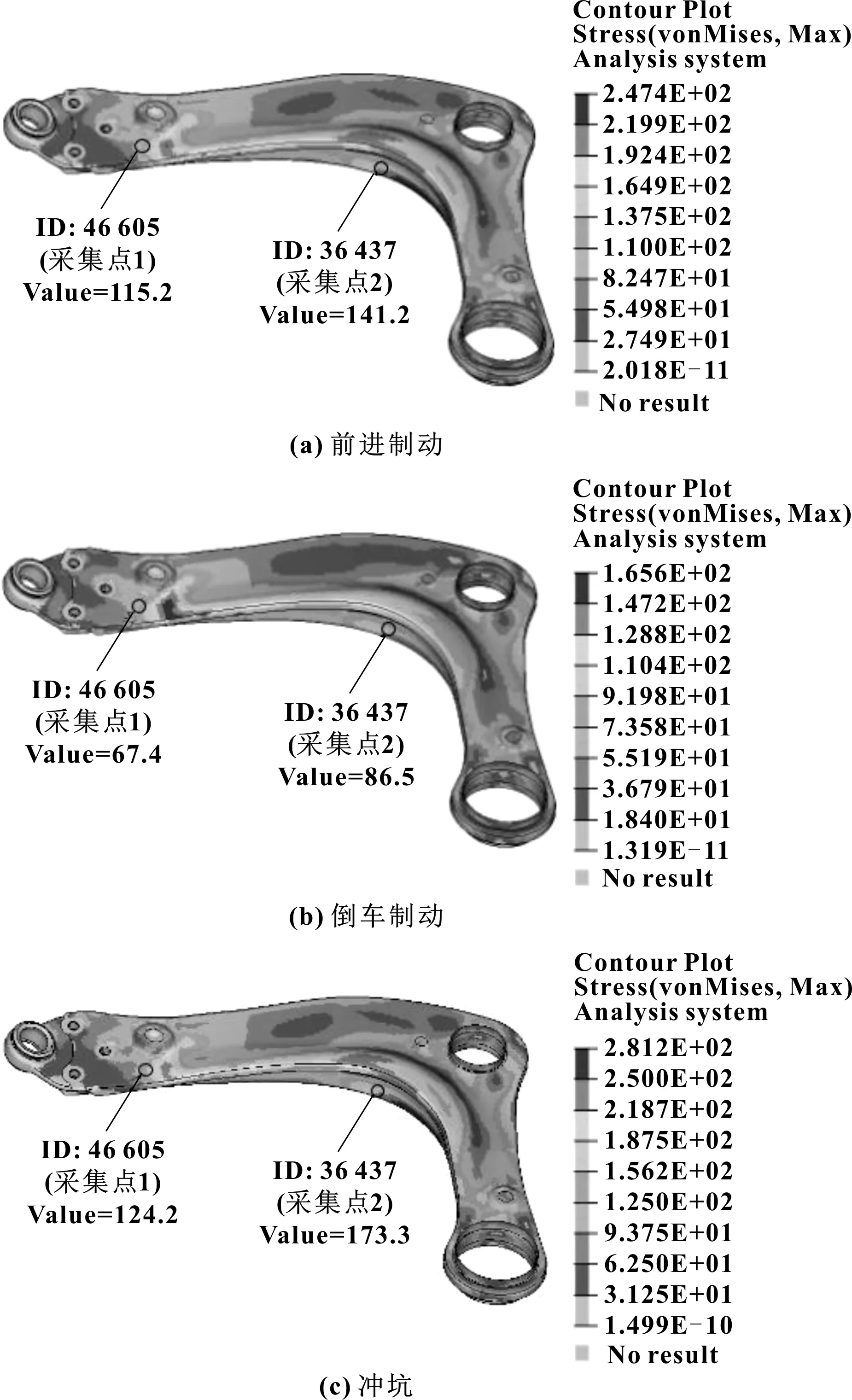
图7 典型工况下应力计算结果

表7中对比了两个采集点的应力计算结果与试验结果。从表7中可知：计算值与试验值最大相对误差+14.8%，最小误差+3.9%，平均误差9.4%。计算结果与测试结果有较好的一致性，误差在可接受范围内。

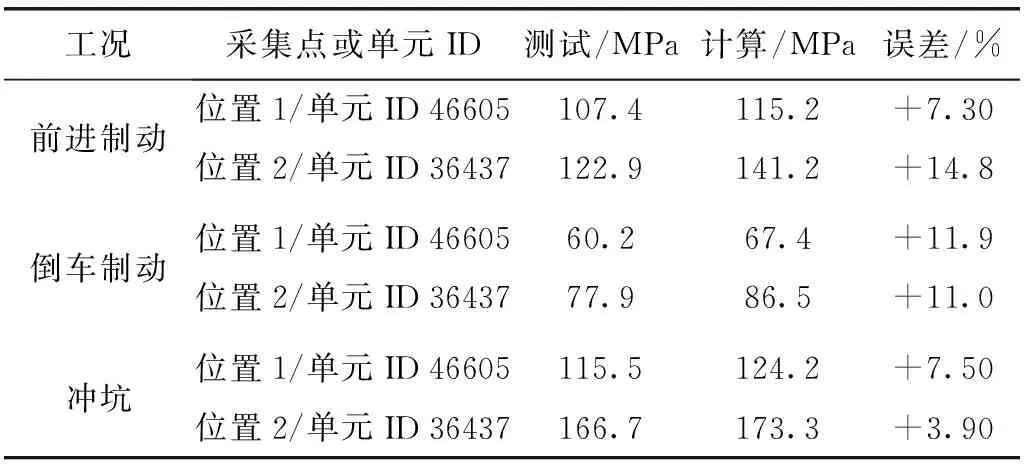
表7 典型工况下的计算与测试对比结果

3.2 疲劳计算与测试结果对比

疲劳计算需先完成单位载荷应力的计算，根据上述已标定的有限元模型进行单位载荷下的应力计算。计算单位载荷应力时，模型边界处理与实际台架试验情况一致。再分别编辑好单轴载荷块与多轴载荷块对应的载荷块谱循环文件，再采用nCode-Design life模块进行疲劳计算。

分别计算得到单轴和多轴两种载荷块的台架疲劳寿命结果如图8所示。对比区域A、B各单元计算结果见表8。

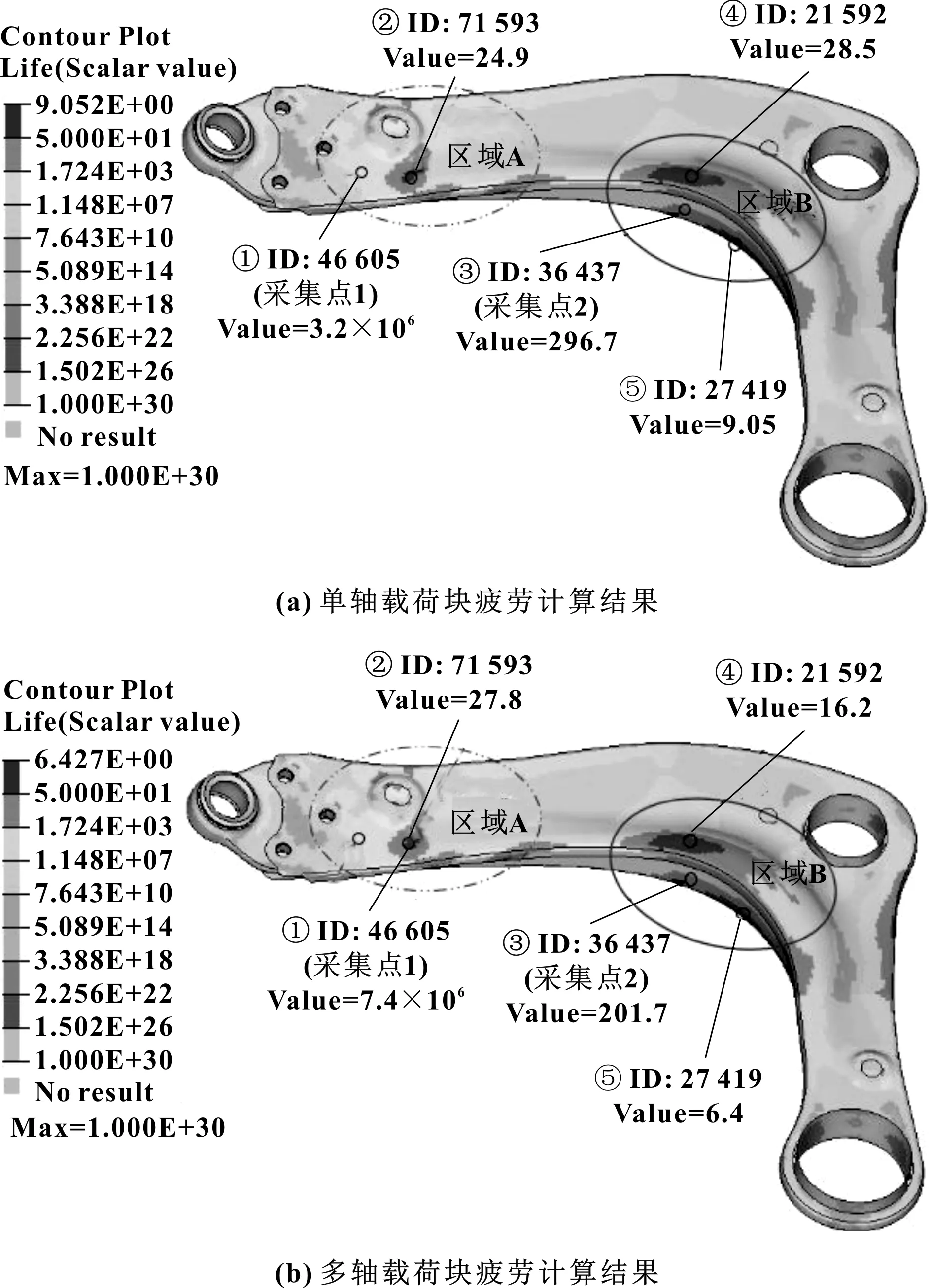
图8 两种载荷分块疲劳计算结果

区域A与区域B试验已采集测试点1和2试验场道路的应变结果，再根据该材料的S-N曲线计算得到位置1和2的真实寿命值见表8。

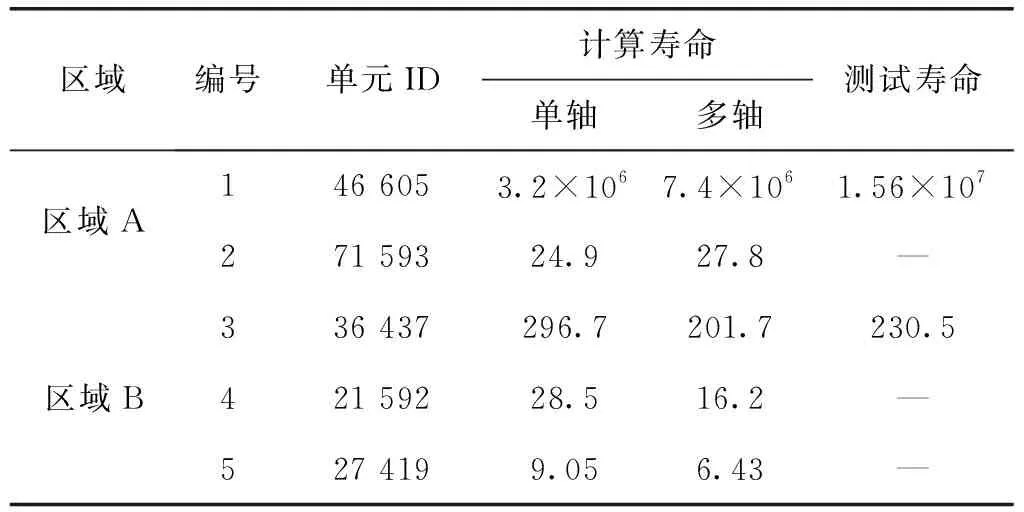
表8 两种载荷分块疲劳计算结果对比

经对比单轴载荷分块与多轴载荷分块疲劳计算结果与实测对比结果发现：(1)两种载荷分块分级方法预测的寿命分布基本一致，但寿命存在梯度差异，单轴载荷块分级预测的最小寿命为9.04，多轴载荷块分级为6.43。(2)两种方法预测的寿命分布存在差异：图中区域A单轴块对寿命预测结果相对于多轴载荷块寿命偏低；区域B单轴载荷块对寿命的预测相对于多轴载荷块寿命偏高。(3)另对比区域A、B采集点1和采集点2的测试结果，发现多轴载荷块相对于单轴载荷块对寿命的预测更为接近，精度相对较高。