北斗三号卫星导航信号接收机端伪距偏差建模与验证

毛飞宇，龚晓鹏，辜声峰，王琛琛，楼益栋

1. 武汉大学卫星导航定位技术研究中心，湖北 武汉 430079; 2. 北方信息控制研究院集团有限公司，江苏 南京 211153

北斗三号全球导航卫星系统(BDS-3)由中国自主建设运行，是北斗系统建设三步走中的最后一个阶段，于2020年7月31日宣布正式开通，包括24颗中圆地球轨道(MEO)卫星，3颗地球同步轨道(GEO)卫星和3颗倾斜地球同步轨道(IGSO)卫星[1-3]。与北斗二号相比，BDS-3不仅向下兼容B1I和B3I信号，还增加了B1C、B2a、B2b和B2(B2a+B2b)这4个新信号[4-5]。

为了简化GNSS数据处理，通常认为硬件延迟较为稳定，且对于码分多址(CDMA)的导航卫星系统，硬件延迟为卫星端和接收机端硬件延迟之和，其中卫星端对所有接收机相同，而接收机端则对同一系统内所有卫星相同[6]。但是相关研究表明，上述硬件延迟处理方法忽略了硬件延迟时空变化以及与接收机类型相关的偏差。

一方面，在北斗二号卫星中发现了由卫星星内多路径引起的与高度角相关的群延迟变化，其幅度可以超过1 m[7-8]。针对这一问题，文献[9—11]相继提出几种不断优化的改正模型，经验证，模型改正可以显著提升宽巷小数周偏差(FCB)解算精度[12]。文献[13]对新一代BDS-3信号进行了初步评估，结果表明，所有信号均不存在与高度角相关的群延迟变化问题。另一方面，接收机的不同硬件配置(例如相关器间隔、前端带宽等)会使GNSS信号在码元对齐时引入偏差，进而导致不同类型接收机、不同卫星的伪距观测值产生系统性偏差(即伪距偏差)[14-18]。该偏差无法被卫星钟差或接收机钟差吸收，会影响基于混合类型接收机网的GNSS精密数据处理，如卫星差分码偏差(DCB)估计[19]、卫星钟差估计[20]、模糊度固定和精密定位等[21-22]。针对该偏差的建模改正，文献[20]的研究表明，对不同类型接收机B1I/B2I无电离层组合的伪距偏差进行按接收机类型建模改正，可以显著提升初始钟差估计结果及双频伪距定位精度。在此基础上，文献[21]分别计算了B1I、B2I和B3I这3个频率上与接收机相关的伪距偏差，并验证了其可以提升模糊度固定成功率、定位精度及收敛时间。然而，对于BDS-3卫星，还缺乏对其伪距偏差建模的相关研究。

为了进一步提升基于混合类型接收机网的BDS-3多频精密数据处理性能，有必要研究不同接收机类型间BDS-3的伪距偏差特性。本文首先对偏差建模方法进行了简单介绍；然后对BDS-3与接收机类型相关的伪距偏差进行了特性分析与建模；最后通过卫星DCB估计与单频伪距定位对改正模型的有效性进行了验证。

1 数学方法与模型

1.1 GNSS基本观测方程

传统的GNSS观测模型将硬件延迟分为接收机端与卫星端两部分，表达式如下

(1)

当考虑伪距观测值存在与接收机类型相关的伪距偏差时，式(1)中的伪距观测方程可转化为如下形式

(2)

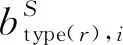
1.2 接收机伪距偏差建模方法

(3)

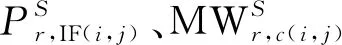
(4)

(5)

(6)

(7)

基于式(5)—式(7)，可以求得不同频率与接收机类型相关的伪距偏差如下

(8)

2 试验与分析

本节基于以上方法，首先对BDS-3不同类型接收机的伪距偏差进行分析与建模，接着将其用于卫星DCB估计和单频伪距定位以验证模型的正确性和有效性。

2.1 数据说明

国际GNSS服务(IGS)组织2012年提出了多GNSS试验计划(MGEX)项目[25-26]，由中国建设的国际GNSS监测评估系统(iGMAS)近年来也建成了数十个可采集多GNSS信号的跟踪站[27-28]。本文采用MGEX、iGMAS两个测站网部分站点数据进行研究，数据时间为2020年DOY 177—DOY 210，表1按接收机品牌及版本分类总结了本文使用的站点名称及可观测到的BDS-3伪距类型。

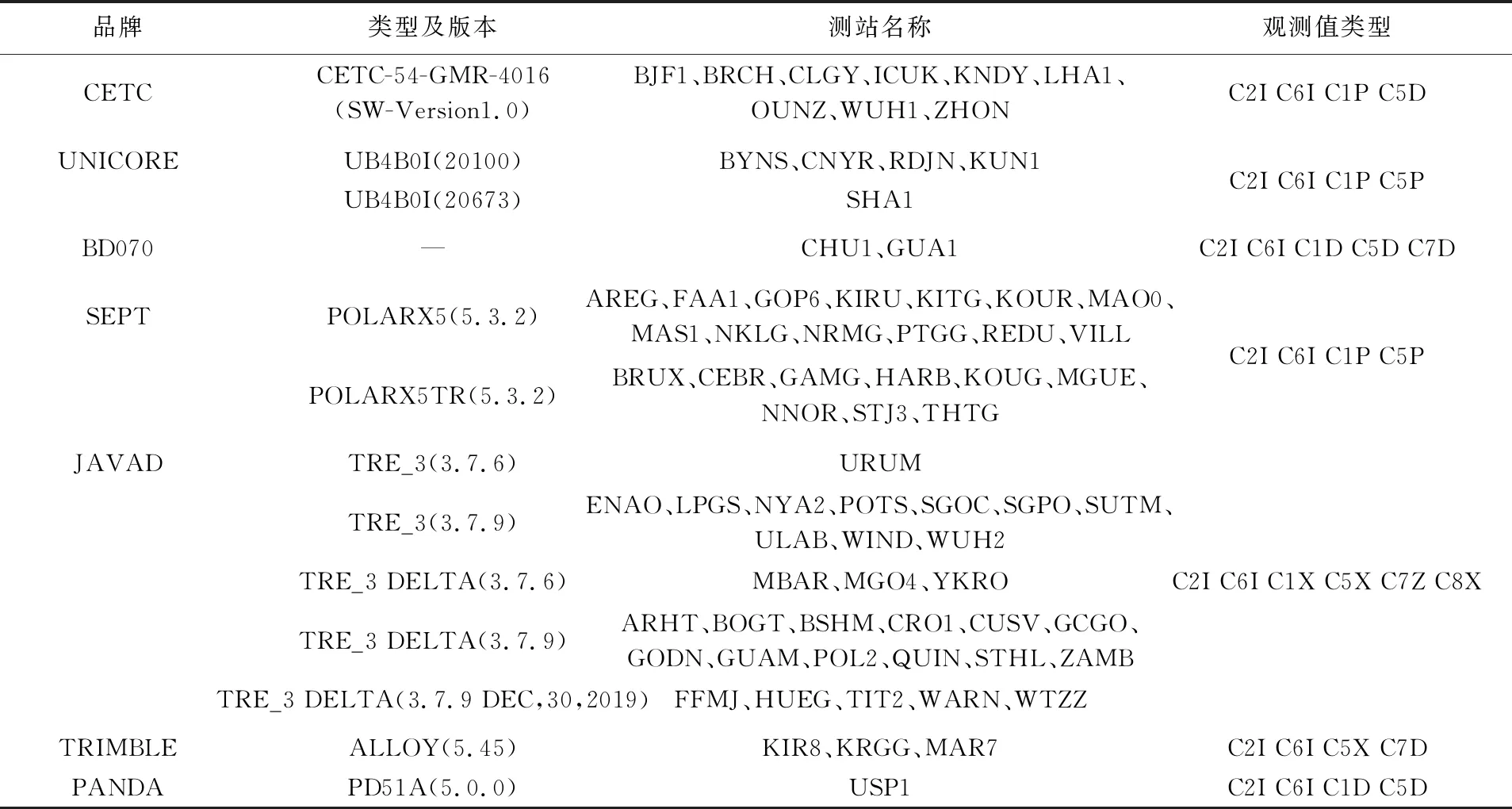
表1 不同品牌接收机信息、相应测站列表及可观测BDS-3伪距信号类型

2.2 伪距偏差分析与建模

由式(4)—式(8)，本文采用C2I/C6I观测值计算MW及IF组合，对于IFGF组合，计算了C2I/C6I与多种BDS-3新信号(C1P、C5P、C7D等)组合的伪距偏差。其中，计算伪距残差采用了德国地学研究中心(GFZ)提供的精密星历，且测站坐标以事后静态解固定。

图1以C19和C30两颗卫星为例，给出了不同品牌接收机从2020年DOY 177—DOY 210的MW/IF组合平均伪距偏差值，不同颜色代表不同品牌接收机。从图中容易看出，不同品牌接收机之间BDS-3卫星C2I/C6I的MW和IF组合均存在与接收机类型有关的偏差。例如，TRIMBLE与SEPT两个品牌接收机C19卫星的MW组合伪距偏差相差在1.1 ns左右，它们的IF组合相差则高达6.0 ns；而同品牌接收机则比较一致，但是JAVAD品牌某版本的接收机与其他版本也存在一定偏差，因此将其单独分为一类，在图中表示为JAVAD DEC。这两类因版本不同被区分的接收机对于C19和C30卫星的MW组合均相差了大约0.2 ns，IF组合则分别相差约1.2 ns和0.9 ns。

图2给出了C19和C20两颗卫星不同站点的IFGF组合伪距偏差情况，图中不同的颜色代表不同的接收机，三角形、圆及五角星不同形状分别代表1D/5D/7D、1P/5P及1X/5X/7X，标注的1D、1P为与C2I/C6I组合的信号类型，如1D表示为C2I/C6I/C1D的IFGF组合。由图2可知，IFGF组合伪距偏差也表现出和MW/IF组合类似的性质，在不同品牌接收机甚至同品牌不同版本接收机间存在一定的系统偏差，例如CETC品牌接收机C30卫星C2I/C6I/C1P的IFGF组合伪距偏差分布在-0.6 ns左右，而UNICORN和SEPT两个品牌则分别分布在-1.6 ns和0.9 ns左右；JAVAD两类接收机C19卫星C2I/C6I/C5X的IFGF伪距偏差差异约为0.6 ns。

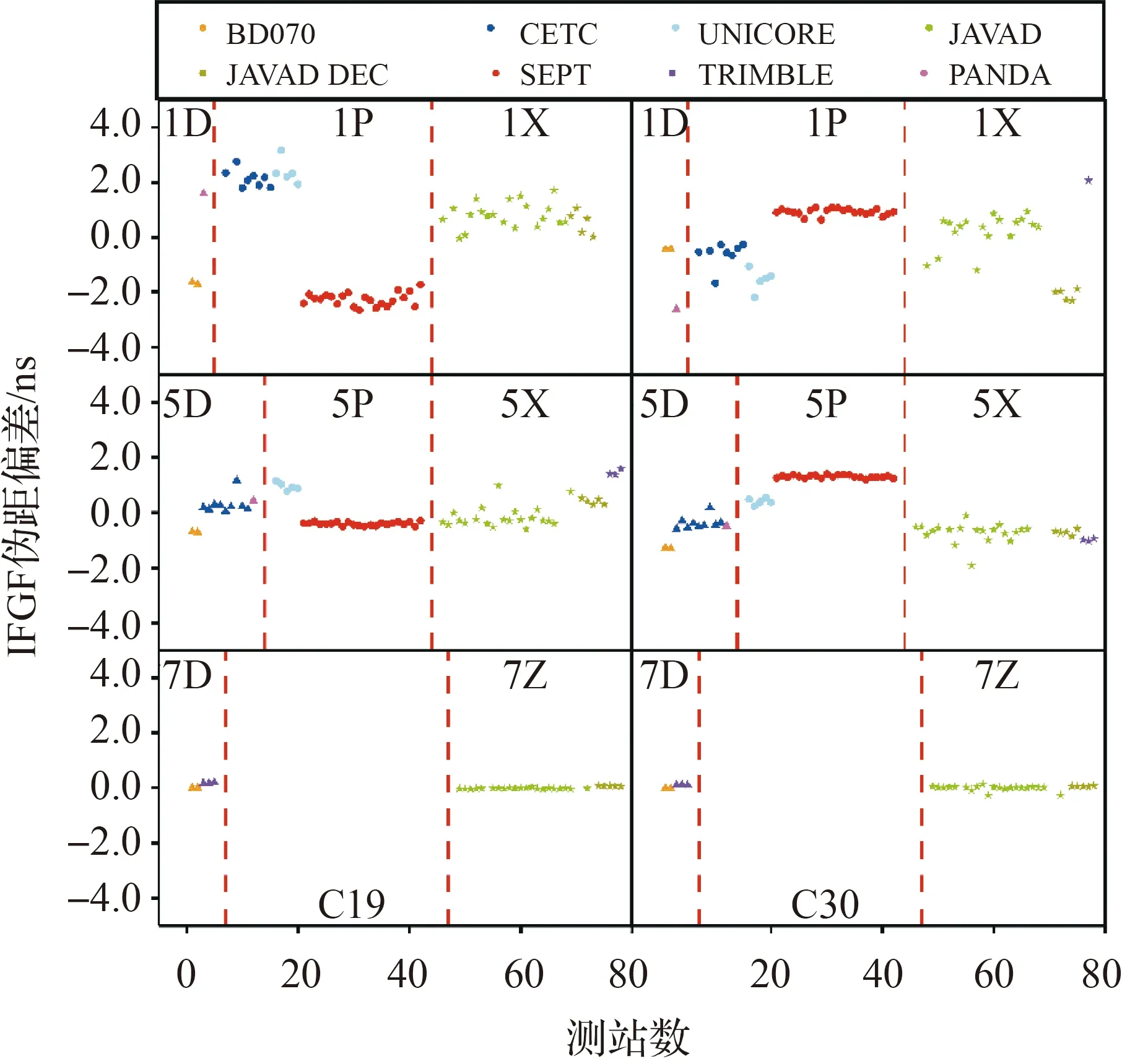
图2 IFGF组合平均伪距偏差Fig.2 Average pseudorange bias of IFGF combination

图3是不同品牌接收机每天平均IFGF组合伪距偏差在不同日期间的STD值。虽然IFGF组合放大了原始观测的噪声，但从图中可以看出，绝大部分接收机BDS-3卫星IFGF组合不同日期间的STD均处于0.05 ns以下，而PANDA接收机表现相对较差可能因为仅有的一个站点观测质量不理想，但总体可以说明BDS-3卫星与接收机类型相关的伪距偏差比较稳定，因此可以用一个常数对其进行改正，这与文献[21]中北斗二号伪距偏差特性一致。

图3 IFGF组合伪距偏差不同日期间STD值Fig.3 STD values of pseudorange bias for IFGF combination across different days

基于MW/IF/IFGF组合伪距偏差结果，利用式(8)可以计算BDS-3不同频率原始与接收机类型相关的伪距偏差改正值(限于文章篇幅，改正值可从该网址下载使用：https:∥www.researchgate.net/project/GNSS-Biases/update/5cd2cff83843b0b9825 1d8ed)。图4给出了BDS-3不同接收机的部分伪距偏差改正值结果。由图可知，BDS-3 C2I和C6I的伪距偏差在不同接收机之间可以达到±1.0 ns，例如C19卫星的C2I信号中，BD070和TRIMBLE接收机的差异达到了2.2 ns。而BDS-3新信号上的伪距偏差则大部分在0.5 ns以内，这可能与BDS-3新信号的调制方式有关。

图4 BDS-3与接收机类型相关的伪距偏差改正值Fig.4 Correction values of receiver-related pseudorange bias of BDS-3

2.3 伪距偏差模型DCB估计验证

通过以上分析可知，当采用混合接收机类型的数据估计卫星DCB时，仅将DCB分为卫星端和接收机端两部分会导致伪距偏差部分被吸收到DCB产品中，导致不同基准站网估计的卫星DCB存在偏差。基于文献[29]中提出的DCB估计模型，改正本文的伪距偏差模型可表达成式(9)

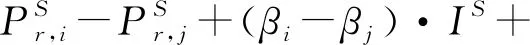
(9)

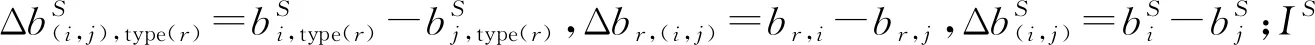
本文使用上述站点及另外61个MGEX站点(JAVAD：2；SEPT：51；TRIMBLE：8)2020年DOY 211—DOY 241的数据，分别基于不同的测站组，通过以上方法计算了BDS-3卫星未改正与改正偏差模型后的DCB结果，通过3种方案比较卫星DCB一致性来验证本文伪距偏差模型。表2给出了3种方案的详细信息。

表2 3种方案比较策略

图5给出了3种方案部分信号间的DCB差异，蓝色和红色分别代表未改正和改正后的不同方案BDS-3卫星DCB差异，标注的统计值为差异值的平均值。由图5可以看到,在未改正及改正后，不同站网估计的卫星DCB差异值变化明显。其中，在未改正本文模型时，方案1估计的北斗三号C2I-C6I、C1P-C5P和C2I-C7D信号间DCB差值分别为0.58、0.33和0.67 ns。当改正本文模型之后，iGMAS和MGEX两类站网估计的卫星DCB的差异分别减小0.05、0.12和0.19 ns，分别降低91.6%、64.7%和71.9%。此外，C1P-C5P的DCB差异值在未改正前已处于较低的水平，这可能是以上两种观测信号在不同类型接收机间的伪距偏差量级较小或者目前接收机类型较少引起的，仍需要更多可以观测到这两种信号的接收机来进一步研究。方案2估计的北斗三号C2I-C6I、C6I-C1P信号间DCB差异在使用本文模型改正后分别降低了96.0%和90.0%。而方案3中所有站点估计的C2I-C6I信号间DCB值与广播星历TGD值的差异在模型改正后降低较少，仅为24.4%，这是因为本文估计卫星DCB的接收机与TGD估计的接收机类型不一致。

表3列出了3种方案BDS-3卫星所有信号DCB差异统计值，由表可知，通过本文伪距偏差模型改正可以提升所有类型的卫星DCB一致性，iGMAS和MGEX两个接收机站网估计的卫星DCB差异可以减少16.3%～91.6%。除SEPT接收机外，所有站点与仅用SEPT接收机站点估计的卫星DCB差异可以减少26.6%～96.0%。

表3 3种方案BDS-3卫星DCB差异均值

2.4 伪距偏差模型定位验证

本节利用单频伪距单点定位验证本文伪距偏差模型的有效性。由于目前IGS提供的卫星钟差和卫星DCB产品尚未考虑伪距偏差影响，因而需要重新估计卫星钟差与卫星DCB产品[20]。其中卫星轨道产品使用德国地学中心(GFZ)提供的事后精密轨道，电离层采用欧洲定轨中心提供的CODG产品，卫星钟差产品和卫星DCB产品则利用MGEX网和iGMAS网基准站分别改正和不改正伪距偏差产品解算得到两组产品，限于篇幅，详细的处理策略参考文献[21]。

图5 3种方案估计DCB的差异Fig.5 BDS-3 satellite DCB difference for three cases

图6给出了15个iGMAS站是否改正本文伪距偏差的单频伪距定位精度，统计值为各个测站2020年DOY 211—DOY 241的平均RMS值。由图可知，所有站点水平方向和高程方向定位精度在模型改正后均有不同幅度的提升，水平方向和高程方向模型未改正时平均RMS分别为0.65和1.06 m，模型改正后分别为0.56和0.94 m，精度分别提升了13.9%和11.0%。

图6 单频伪距单点定位精度对比Fig.6 Comparison of single frequency single point positioning

3 结 论

本文采用iGMAS网与MGEX网数据分析不同接收机类型间BDS-3卫星伪距偏差特性，试验结果表明，不同品牌接收机BDS-3卫星伪距偏差存在一定差异，例如TRIMBLE与SEPT两个品牌接收机C19卫星的MW组合和IF组合伪距偏差分别相差约1.1 ns和6.0 ns；而同品牌接收机的BDS-3伪距偏差相对比较一致，且该伪距偏差在一个月内较为稳定，绝大部分接收机类型的偏差STD优于0.1 ns。

根据偏差特性，本文按接收机类型建立了北斗三号伪距偏差改正模型。通过不同接收机类型估计的卫星DCB产品一致性和单频伪距定位对模型有效性进行了验证。结果表明，在未改正本文模型时，使用iGMAS和MGEX网估计的BDS-3卫星存在最大0.74 ns的差异，而改正本文的伪距偏差模型后，两种接收机站网估计的卫星DCB一致性得到了显著提高，其差异小于0.19 ns，相比未改正模型时，卫星DCB差异降低了16.3%～91.6%。此外，模型改正后单频伪距定位水平和高程方向平均RMS值分别降低了13.9%和11.0%。