不同孔隙率对高应力水平下混凝土强度的影响研究

彭 哲， 万 勇， 刘文劼， 黄圣平， 秦 倩

(1.湖南省水运建设投资集团有限公司， 湖南 长沙 410011; 2.湖南省交通科学研究院有限公司， 湖南 长沙 410015)

桥梁作为交通线路的咽喉要道，对于保证交通的安全运营起着重要作用，到 2017 年底，仅公路领域，桥梁的总数已经达到83万座以上，其中混凝土桥梁占 90%以上[1]。大体积混凝土在长大桥梁中的应用日益广泛，且主要用于重要结构的承载部位。即使不考虑温度应力，大体积混凝土中的应力水平也可以达到很高，若其值接近或超过混凝土强度或极限应力时，混凝土结构将存在巨大安全隐患。因此，了解高应力水平下混凝土的强度成为了保障混凝土结构安全的关键之一[2]。

在混凝土三轴压缩试验中，通常可采用一系列标准来定义混凝土的极限状态，例如可以将应力 — 应变曲线趋于水平时作为极限状态考虑，或者将试样从体积收缩到体积膨胀过渡时作为极限状态考虑，混凝土的极限状态往往与骨料组分、水灰比、外加剂、湿度等因素有关。Wang等[3]对大体积混凝土进行了三轴静力和动力试验，发现相比干燥混凝土，饱和状态混凝土抵抗变形的能力明显更低，更容易达到极限状态，这归因于孔隙水粘稠度的变化。Forquin等[4]和Piotrowska等[5]评估了孔隙游离水对混凝土在静态和动态荷载作用下受力性能的影响，发现饱和样品的强度比干燥样品平均少23%。Farhad等[6]开展了不同尺寸的高强混凝土三轴压缩试验，通过对试验数据进行最小二乘拟合而得到高强混凝土的破坏面。Setunge等[7]指出添加硅粉后超高强度混凝土的强度值明显增加，并采用双参数模型对受侧限混凝土的破坏包络进行表述。国内方面，李青松等[8]对混凝土进行三轴压缩试验，发现混凝土的破坏存在一个极限围压值，当围压超过该值时，混凝土的变形由应变软化向应变硬化过渡。杨海峰等[9]研究了围压、再生粗骨料成分对高强混凝土的影响，发现再生骨料混凝土的破坏形态较普通混凝土有特殊性，其一般的破坏形态为斜面剪切破坏，并提出了高强混凝土应力 — 应变曲线的本构方程。闰东明等[10]对处于三向应力状态下混凝土的强度和变形进行了研究，提出了基于应力的混凝土结构强度和变形经验公式，可为混凝土的工程应用提供指导。阎培渝等[11]研究了养护条件对高强混凝土强度的影响，对比了不同温度下混凝土抗压强度的变化。

上述研究从应力状态、骨料成分、养护条件等角度探讨了混凝土强度或极限应力的影响因素，除此之外，孔隙率也是影响混凝土强度的重要指标，混凝土的孔隙率由连通孔隙、半连通孔隙以及封闭孔隙3部分组成，连通孔隙和半连通孔隙可以使水通过、排出或储存，所以称为有效孔隙；而封闭孔隙由于是完全闭塞，水流不能进入其中，相应被称为无效孔隙[12]，而有效孔隙和无效孔隙各自对混凝土的影响研究鲜有开展。本文从混凝土的孔隙率角度出发，通过对3种不同类型的混凝土开展三轴压缩试验，研究混凝土应力 — 应变关系和强度的变化规律，探讨在不同围压下有效孔隙和无效孔隙各自作用的显著程度，并建立体现孔隙率影响的强度预测模型，为工程中计算混凝土的强度提供参考。

1 试验过程

1.1 试验材料

试验用的3种混凝土均为自搅拌生成，表1列出了其配比和主要参数。其中OC(普通混凝土)大致按照普通C35混凝土要求进行配置，立方体抗压强度标准值fck为22.6 MPa，另外2种混凝土为LPC(低性能混凝土)和HPC(高性能混凝土)，为了有针对性地体现孔隙率和饱和度对混凝土性能的影响，3种混凝土的骨料组分尽可能保持相同。对于LPC，加入引气剂以增加含气量和孔隙率，其fck最低，约18.2 MPa；对于HPC，调低水灰比(0.33)以增加强度，加入增塑剂以改善和易性，同时加入硅粉来填充孔隙、降低孔隙率，这使得HPC的fck达到约60.3 MPa。

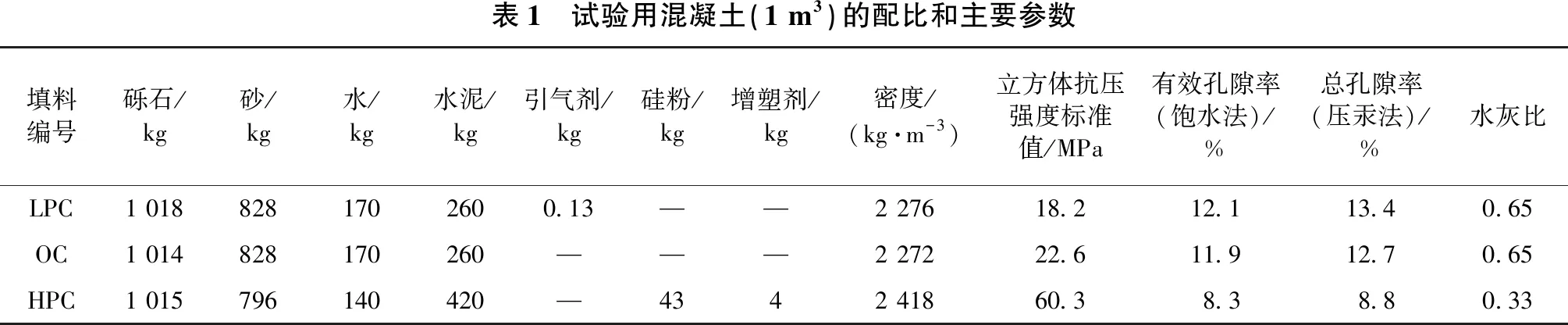
表1 试验用混凝土(1 m3)的配比和主要参数填料编号砾石/kg 砂/kg 水/kg水泥/kg引气剂/kg硅粉/kg增塑剂/kg密度/(kg·m-3)立方体抗压强度标准值/MPa有效孔隙率(饱水法)/%总孔隙率(压汞法)/%水灰比LPC1 0188281702600.13——2 27618.212.113.40.65OC1 014828170260———2 27222.611.912.70.65HPC1 015796140420—4342 41860.38.38.80.33

1.2 试样制备及加载

参照《公路工程水泥及水泥混凝土试验规程》(JTE E30—2005)[13]，在自制的正六面体(150 mm×150 mm×150 mm)模具中浇筑混凝土试块，放入养护室中24 h后拆除模具，继续养护28 d，进行轴心抗压强度标准值测试后，在混凝土块上钻芯取样作为三轴压缩试验的试样，试样的尺寸为直径150 mm、高度300 mm，再将端面进行磨平处理。

对3种类型的混凝土均设置2个饱和度进行研究，分别为12%和100%，其中干燥样直接在烘干机中烘干24 h，经测定其饱和度大致为12%，饱和试样在蒸馏水中浸泡7 d，直至其质量不再明显变化，认为其接近100%饱和度，并通过式(1)进行验算[14]：

(1)

式中：msat为饱和试样质量；msr为预计达到指定饱和度时试样的质量；mw为孔隙水质量。

此外，对OC还设置了另外3个中间饱和度，分别为44%、78%、93%，为达到上述中间饱和度，参照文献[14]的做法，将饱和混凝土试样放入湿度控制密封容器，将相对湿度设置为44%、78%、93%，温度控制为20 ℃，期间不断通入CO2，待试件质量基本不变时，认为其接近指定的饱和度，同样采用式(1)进行验算。

试验仪器为微机控制电液伺服岩石三轴试验机，最大加载围压为100 MPa，最大加载轴力为9 MN。所有试验均按同一加载路径进行加载，即按0.17 MPa/s的速率施加围压，达到指定围压后，在轴向施加轴压，位移速率控制在20 μm/s左右，在试验过程中测定试样的轴向应变εx。

2 偏压下力学行为

在本文中，定义εx为轴向应变，σx为轴向应力，p为围压，平均应力σm=(σx+2p) / 3，轴向偏应力q=σx-p，简称Sr≈12%的试样为干燥样。图1显示了5、20、60 MPa围压下HPC和LPC试样轴向偏应力q与轴向应变εx的关系。

可以看出关系曲线可以分为A、B两类，A类曲线即偏应力到达一定值后趋于稳定，饱和样主要为此类曲线；B类曲线即偏应力持续增加，干燥样主要为此类曲线。可以看出，在低围压下，同一轴向应变下HPC的偏应力明显更高，抵抗变形的能力更佳，但在高围压下二者的偏应力比较接近。事实上，对于HPC而言，在高围压下孔隙率下降、密度增加，水泥的胶凝作用逐渐削弱，力学性能逐渐被粗骨料所控制，由于HPC与LPC的粗骨料组分相似，因此在高围压下二者的偏应力或强度十分接近。

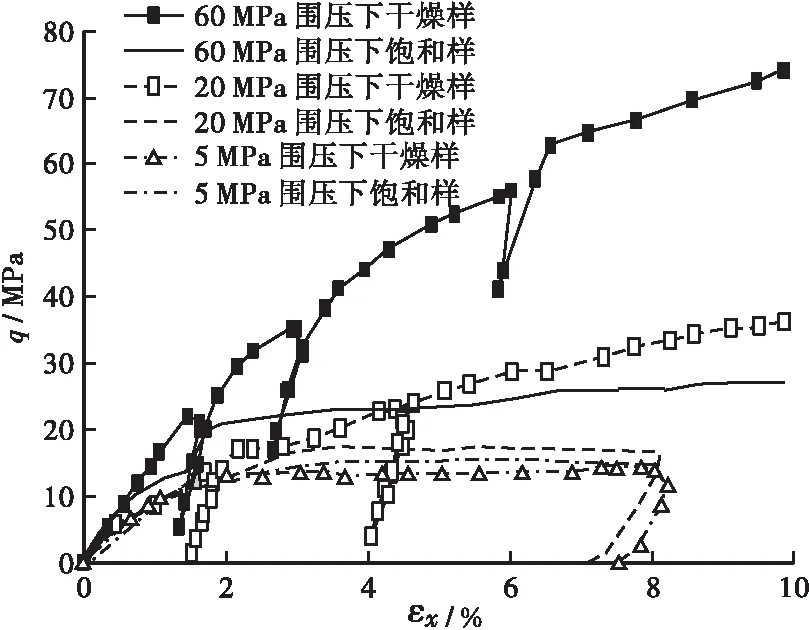
a) LPC

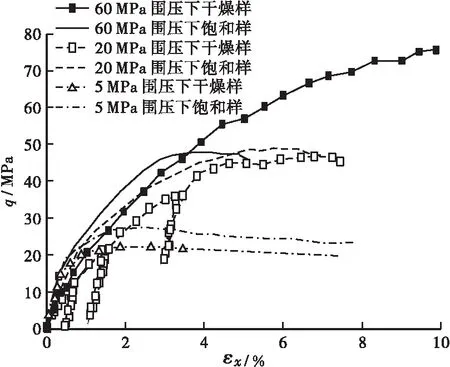
b) HPC

图2显示了围压为40 MPa时3种混凝土偏应力q与轴向应变εx的关系。3种混凝土孔隙率的大小排序为：LPC>OC>HPC，由此可以看出孔隙率越大，饱和度对力学性能的影响越显著。对于LPC和OC的饱和样，q最大值约为20 MPa，这可能是由于LPC和OC二者的有效孔隙率比较接近所致，而对于HPC的饱和样，q最大值约为50 MPa。对于干燥样，3种混凝土的关系曲线比较类似，偏应力持续上升，但在同一轴向应变下，HPC的q值并不是最大，这可能是由饱和度轻微的差异所致。由于对3种混凝土实际上采用了相同的养护条件，HPC更加致密，渗透性偏低，其干燥样在烘干后的饱和度可能略高。

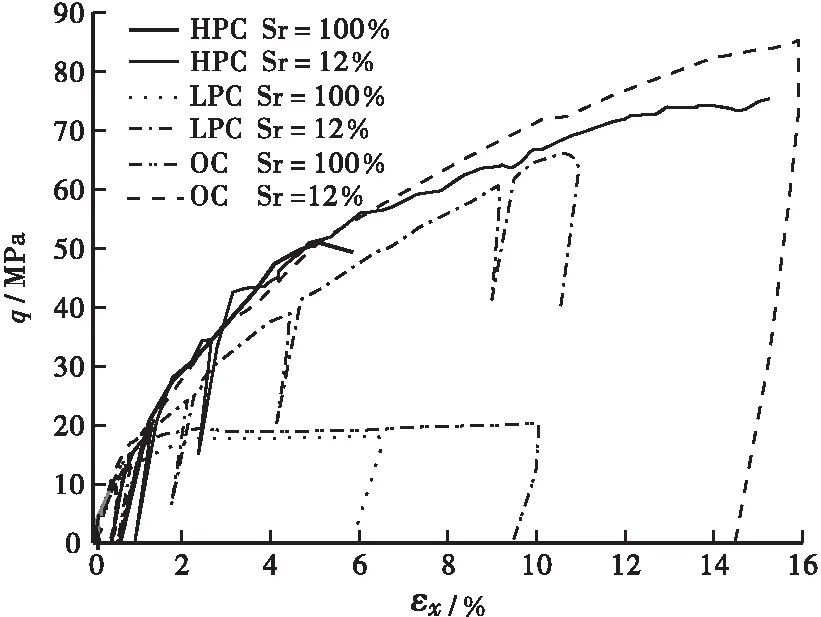
图2 围压为40 MPa时3种混凝土的偏应力 — 轴向应变关系

对于A类曲线，将曲线趋于水平时的偏应力作为强度或极限应力qmax考虑，而对于B类曲线，将试样从体积收缩到体积膨胀过渡时对应的偏应力作为强度或极限应力qmax考虑。图3分别为LPC和HPC在2种饱和度下强度qmax与平均应力σm的关系。可以看出，在平均应力较低时饱和样和干燥样的数据点基本重合，但超过某一平均应力的临界值σcr后，饱和样的qmax几乎不再随着σm增加而上升。HPC、LPC的σcr分别约为39.7 MPa和18.9 MPa，可以看出临界平均应力σcr是随着孔隙率增大而减小的。

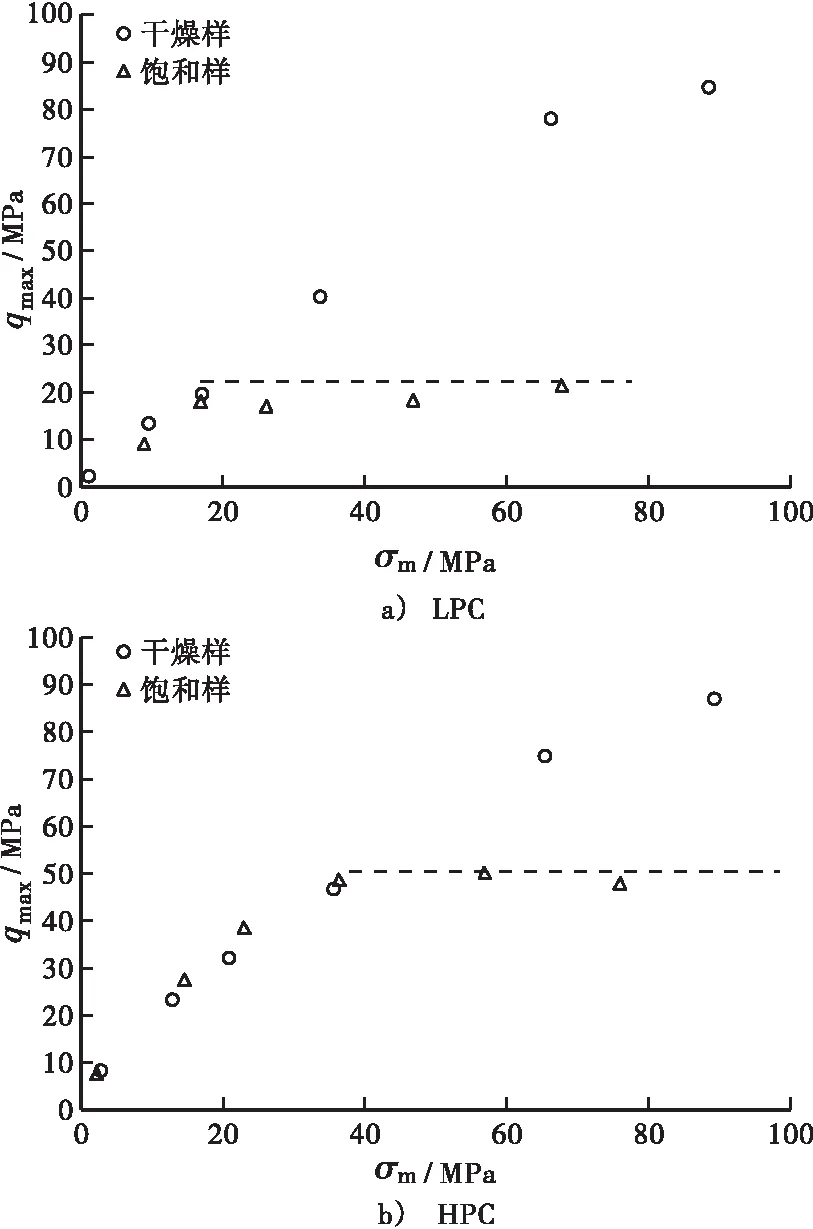
图3 不同平均应力下的强度

图4显示了OC在5种饱和度下强度qmax与平均应力σm的关系。总体来看，当孔隙率一定时，饱和度越大，qmax越小；qmax与σm成正比，但饱和度越大，qmax随σm增加而上升的趋势越弱。与HPC和LPC相比，OC也存在类似的临界平均应力。

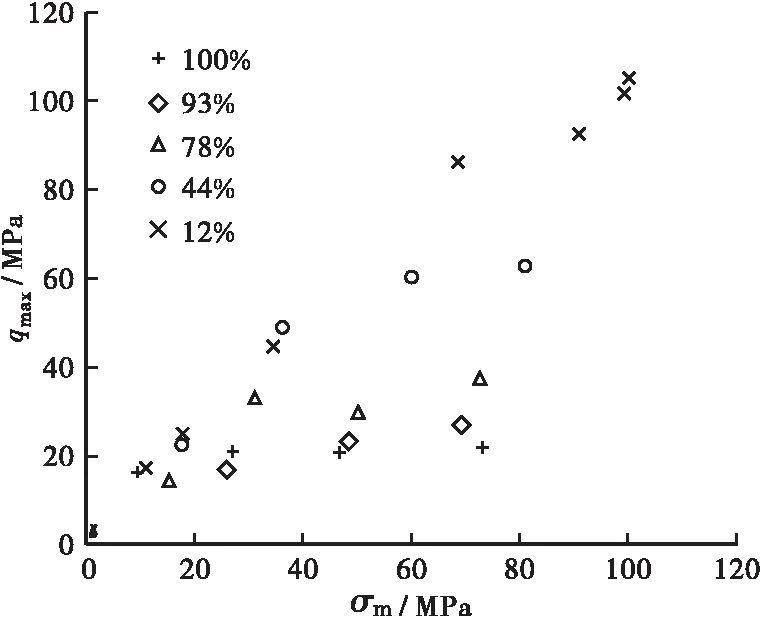
图4 OC在5种饱和度下的强度

图5显示了干燥样qmax，dry与饱和样qmax，sat的比值与围压的关系。可以看出，在各个围压下，随着饱和度由12%向100%变化，HPC强度的扰动较小，但对OC和LPC，扰动明显较大，qmax，dry/qmax，sat值达到HPC该值的2倍以上，说明随着孔隙率增大，强度受饱和度变化的敏感性也在增强。

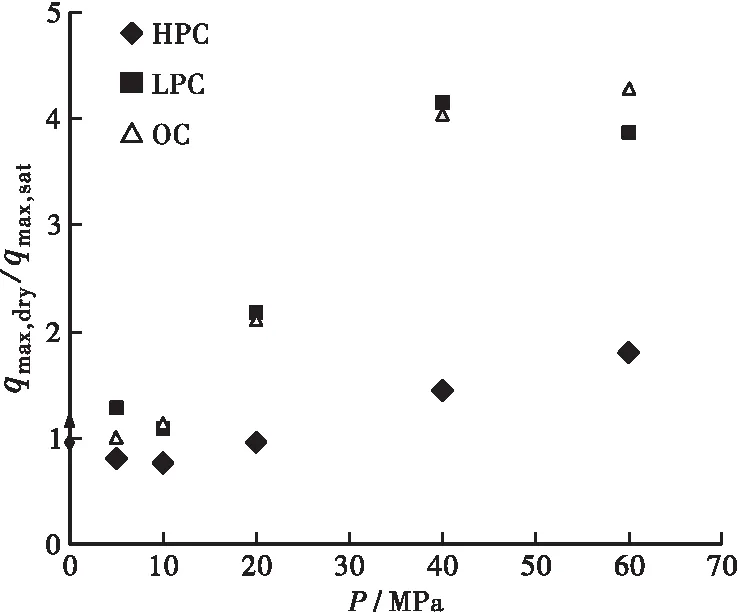
图5 qmax，dry/qmax，sat与围压的关系

3 强度预测

目前对于混凝土强度的描述准则包括线性模型(M-C模型、D-P模型等)、抛物线模型和幂函数模型。在较低的平均应力下，线性模型和抛物线模型往往会高估混凝土的强度，本文的模型既要能适应高应力水平，也要能适应低应力水平，从而具备普适性，因此没有选择线性模型和抛物线模型。本文采用幂函数模型来对试验结果进行描述，其基本形式如下：

qmax=a(b+σm)α

(2)

该公式还可以写成如下形式：

(3)

式中：q1为参考剪应力；α为对数图上的直线斜率；σ0为参考平均应力。

q1和α主要受完全致密时混凝土的骨料组分影响，由于本试验中3种混凝土的组分类似，因此假设3种混凝土的q1和α是相同的；而σ0可考虑为无侧限条件下混凝土的某一强度指标，本文采用立方体抗压强度标准值fck。图6为采用式(3)对本文干样试验数据的拟合，其中拟合参数为q1=98 MPa，α=0.81，可以看出尽管这3种混凝土的力学性能差异很大，但总体的qmax～(fck+σm)关系与幂函数十分接近，而且假设3种混凝土的q1和α相同也是可靠的。

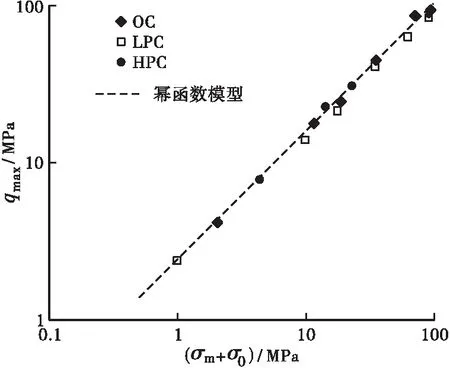
图6 采用式(3)对最大偏应力的拟合

在混凝土立方体抗压强度试验中，围压为0，此时混凝土的qmax与轴心抗压强度标准值fck接近，而平均应力σm则等于fck的1 / 3，在式(3)中用fck和(fck/ 3)分别替换qmax和σm，可推导出：

(4)

将式(3)和式(4)联立，可以依赖fck的破坏准则或极限应力预测模型：

(5)

利用上述模型，可在仅掌握fck的情况下预测不同σm条件下的qmax，最大预测误差仅为8.6%。

此外，根据图3和图4可知，3种混凝土均存在临界平均应力σcr，当σm超过σcr后，强度qmax几乎不再受σm的影响，基本保持恒定。如前所述，σcr是随着有效孔隙率增大而减小的，因此定义σcr与有效孔隙率φ的关系如下：

σcr=σc p 0-κφ

(6)

式中：σc p 0为极限平均应力，为完全致密(φ=0)条件下混凝土的平均应力，通过线性拟合得出该值约为85.1 MPa；κ为控制σcr随孔隙率增加的衰减程度，大约为547.4 MPa。最终建立的临界平均应力预测模型如下：

σcr=85.1-547.4 φ

(7)

4 结论

通过对OC、LPC、HPC等3种混凝土开展三轴压缩试验，得出如下主要结论：

1)在低围压下，由于HPC的孔隙率更小，产生同一轴向应变时HPC所需的偏应力明显更大；而在高围压下，HPC和LPC干燥样的偏应力比较接近。

2)总体来看，在孔隙率一定时，饱和度越大，qmax越小；qmax与σm成正比，但饱和度越大，qmax随σm增加而上升的趋势越弱，这表明对于饱和度较高的混凝土，通过提高侧向约束来增加强度是不经济的。

3)OC和LPC的qmax，dry/qmax，sat值达到HPC该值的2倍以上，说明随着孔隙率增大，强度受饱和度变化的敏感性也在增强。

4) 利用本文式(5)模型，可在掌握fck的情况下预测不同σm下的强度qmax，而且最大预测误差仅为8.6%；利用式(6)模型，可以预测不同孔隙率下混凝土的临界平均应力σcr。