浅析船舶旋回过程及MATLAB仿真

李纪强 张国庆

（大连海事大学 航海学院 大连116026）

引 言

旋回圈几何参数是表示船舶旋回性能的重要指标，是判断船舶旋回优劣的直接依据。一般选择具有实际意义的特征参数来描述船舶的旋回性能。IMO操纵性标准中已经把进距和旋回初径两个参数作为船舶旋回性能的衡准。

船舶大型化已是当今船舶发展的一个趋势，但是由于大型船舶相对较重且惯性大和停船距离长等特点，其均应具备良好的旋回性能。在特殊会遇情况下，为避免发生突发性危险，大型船舶所采取的避碰措施与普通船舶也存在差异，并且大型船舶在船舶旋回过程中所表现出的较明显速度下降这一现象，已引起众多学者的研究和航海驾驶员在实际航行中的运用。

满舵旋回是船舶避碰领域中船舶紧急避让时经常采用的一种避让方法，因此，研究船舶旋回运动过程，分析船舶旋回运动过程中各特征参数的变化以及旋回速降对于船舶避免碰撞，有一定的实际意义。Kempf于20世纪40年代首先提出一种衡量船舶机动性能的试验方法，即Z型试验。此后，在20世纪50年代，野本谦作和诺宾发展了一种对Z型试验结果进行理论分析的新方法——

K

、

T

分析法，其中的

K

、

T

指数可描述船舶操纵性能，所以称其为操纵性指数。戴维逊和李宗波等人又根据大量实船试验和船模试验绘制了回转速降系数与相对回转直径之间关系的曲线。

1 Nomoto模型与K、T指数

1.1 Nomoto模型的建立

1.1.1 船舶平面运动描述

船舶运动数学模型主要建立在两种坐标系上，即惯性坐标性和附体坐标系，如图1和图2所示。

图1 在惯性坐标系和附体坐标系中描述船舶的运动

图2 船舶平面运动描述

船舶运动研究通常仅考虑船舶在水平面内的运动，因此船舶的前进、艏摇和横漂三自由度的运动情况如图2所示。

1.1.2 二阶响应型数学模型

船舶水平面操纵运动的二阶响应模型是将船舶运动线性方程的后两个式子中的

v

消去，仅考虑船舶的两个自由度横漂速度

v

和转艏角速度

r

，船舶操纵运动的线性方程如下

式中：

δ

为舵角输入，系数

a

、

a

、

a

、

a

、

b

、

b

由船舶的基本参数确定。

式（1）可转换为一个描述操舵对艏摇响应的简单方程，即

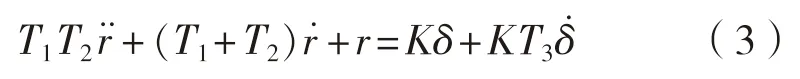
1.1.3 一阶响应型模型

对式（3）作拉氏变换，可由二阶方程推出一阶

K

、

T

方程，并设定初始值为

由此可得到船舶转首对操舵响应的传递函数

式中：

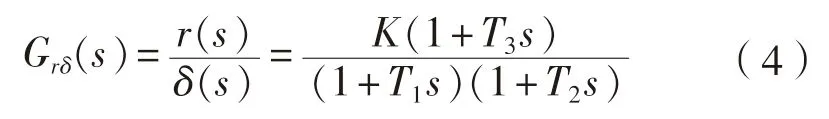
s

为拉普拉斯算子。

此外，对一阶惯性环节的传递函数按幂级数展开，得

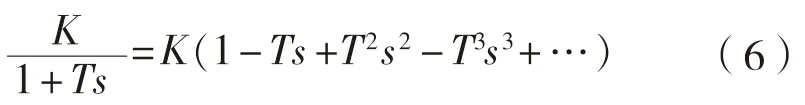
和

该式等价于

这就是船舶操纵运动一阶线性

K

、

T

方程（对于

r

来说），也称为Nomoto模型。

1.2 操纵性指数 K、T

式（10）是描述船舶操纵运动的简单实用方程。野本谦作认为，

K

、

T

是一种描述船舶操纵特性的特征参量，具有明确的物理意义。1.2.1 船舶操纵性指数

K

K

指数是操舵后转船力矩系数与阻尼力矩系数之比所决定的常数，反映了船舶的旋回性的优劣，称“旋回性指数”。

K

值越大，表示舵产生的回转力矩大而阻尼力矩小；反之，

K

值越小，表示舵产生的回转力矩越小而阻尼越大。实际操船中，操船者总是希望

K

值越大越好，表示舵效越好。1.2.2 船舶操纵性指数

T

T

指数是船舶绕其重心

G

竖轴的惯性矩与阻尼力矩系数之比所决定的常数，代表船舶对舵的快速应答性和航向稳定性，反映船舶追随性的优劣，称为“追随性指数”。

T

值越大，表示船舶惯性大而阻尼力矩小；反之，

T

值越小，表示船舶惯性小而阻尼力矩大。

T

也被称为时间常数，该时间越短越好，则舵效越好。所以对于操纵性良好的船舶应具有大的正

K

值和小的正

T

值。

2 旋回要素与参数变化

2.1 旋回圈特征参数

船舶旋回性最能代表船舶的变向性能，历史上对旋回性的研究也最多。当船舶以速度

u

直线航行时，操舵后船舶即在水平面内作曲线运动，其轨迹如图3所示。

图3 船舶旋回圈

船舶重心的瞬时位置为旋回运动起始点，称为执行操作点。由于船舶惯性较大，艏向角

ψ

需改变一定数值后，其轨迹才进入曲率半径为常数的定圆，艏向角再改变一定数值后，转首角速度才变为常数，此时船舶达到了定常旋回，旋回圈的主要参数为：（1）纵距：船舶从旋回开始，艏向转过90

°

时，船舶重心距离初始位置的纵向距离

A

。该值越大，船舶的旋回性越差。（2）横距：船舶从旋回开始，艏向转过90

°

时，船舶重心距离初始航线的长度

T

，该值越小，船舶的旋回性越好。（3）反移量：从船舶初始直航线至运动轨迹向回转圈相反方向横移的最大距离

L

，满舵时约为船宽的1.0～1.5倍。（4）旋回中的船速

V

：船舶旋回过程中，船速不断下降，旋回中的船舶速度与初始船舶速度的比值为船舶旋回速降系数。

2.2 旋回运动过程分析

从船舶运动学角度考察船舶的旋回运动，其运动过程可分为3个阶段，即转舵阶段、过渡阶段和定常旋回阶段。旋回运动过程中运动参数的变化如图4所示。

图4 旋回运动过程中运动参数的变化

2.2.1 初始阶段

在舵角达到规定值之前为船舶旋回初始阶段。在此阶段，船舶发生内倾，产生各自由度的加速度和速度及角速度，在操右舵时，舵横向力的方向为负（向左），转舵力矩的方向为正值（顺时针），且由于船舶惯性较大，因此船舶在此阶段基本保持原直线运动。

2.2.2 过渡阶段

在过渡阶段，舵角达到（

δ

）且不变，船舶前进、横漂、艏摇等自由度上均存在加速度和速度，且加速度在不断变化，船舶发生外倾。

2.2.3 定常阶段

在船舶旋回过程中，在经过一段时间后，船舶各自由度上加速度均为0，速度和角速度为一定常量，此时，船舶进入定常旋回阶段。

2.3 旋回过程速降研究

在船舶旋回运动过程中，会产生船舶运动速度降低的现象。其原因之一是由于旋回运动过程中，横向速度

v

和角速度

r

的存在使船舶处于斜航和和旋转状态，船舶阻力比直航时大为增加；其原因之二是由于螺旋桨通常设计为直航状态时的推进效率最高，而船舶旋回过程中

v

、

r

、

δ

的存在使螺旋桨推进效率大为降低。另外，船舶旋回过程中由于阻力的增大，螺旋桨转速也会相应降低。因此，这些因素都导致船舶旋回运动过程中的船速下降，称为“旋回速降”。

船舶旋回速降与初始船速、船型、载况等诸多因素有关。万吨级船舶一般旋回降速达25%～50%，大型船舶旋回速降更为剧烈，有时甚至可达65%以上。

李宗波等人在研究了国内外关于速降系数的研究后，综合了速降系数的影响因素可以取3个代表性的因素来衡量，分别为旋回性指数

K

′、舵的法向力系数

C

和航向改变量Δ

ψ

。在43艘船舶的基础上，李宗波等人又搜集了4艘超大型船的

K

′、

T

′指数资料，利用47艘船的资料回归分析得到修订的

K

′、

T

′估算公式为

式中：

L

、

B

、

d

分别为船长、船宽和吃水，m；

A

为舵面积，m；

C

为方形系数。修订后的

K

′、

T

′估算公式的拟合优度指标即复相关系数 略有增加，分别达到了0.792和0.851。由修正后的

K

′、

T

′，进行多次最优回归分析，可以得到船舶旋回速降系数估算公式。

式中：Δ

ψ

的单位为（°）。

表1 给出了OPALIA轮压载状态下满舵旋回试验中的速降记录结果。可见定常旋回时的船速约为初始船速的1/5，同样，旋回方向对旋回降速影响不大。

表1 OPALIA轮压载状态下的速降记录kn

本文采用李宗波等人提出的速降估算公式，对30万吨油轮OPALIA轮进行MATLAB仿真验证并与实船结果进行比较，验证了对于李宗波等人研究结果对超大型船舶旋回速降的预报性。进行了压载状态下全速满舵（

δ

= 35

°

）旋回的速降预报。该轮主尺度为：两柱间长

L

= 320 m、船宽

B

= 60 m；试验时，平均吃水

d

= 10.660 m、方形系数

C

= 0.743 4，舵面积比

A

/（

Ld

）=1/35.04。经式（12）计算得到

K

′=1.396 6；舵角35

°

时，舵的法向力系数

C

=1.257 4。图5和图6分别表示OPALIA轮在压载左满舵和压载右满舵（

δ

= 35

°

）情况下的旋回速降实验对比图。图中：蓝色实线表示旋回速降的实时预报，黑色离散点表示OPALIA轮在实际旋回实验中监测到的旋回速降数值。从图5和图6可以看出，旋回速降预报曲线和实际速降数值变化曲线基本一致，由此说明旋回速降预报公式的有效性。

图5 OPALIA轮压载左满舵（35°）旋回速降图

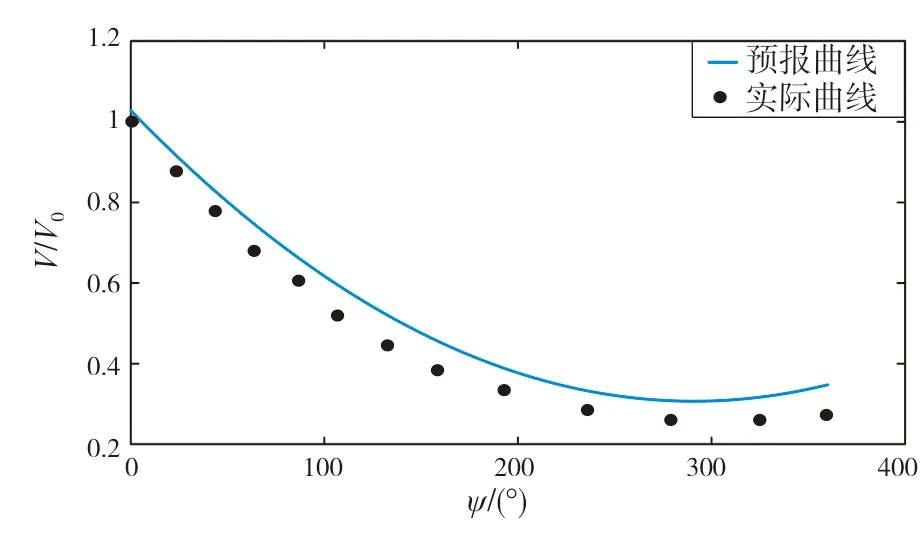
图6 OPALIA轮压载右满舵（35°）旋回速降图

2.4 旋回试验与MATLAB仿真

本节利用MATLAB仿真响应型数学模型，试验对象为大连海事大学教学实习船“育鲲轮”。本节考虑航海仿真条件给出了基于“育鲲轮”的仿真测试结果，外界环境干扰等效为式（14）。

图7表示旋回试验MATLAB仿真流程图。

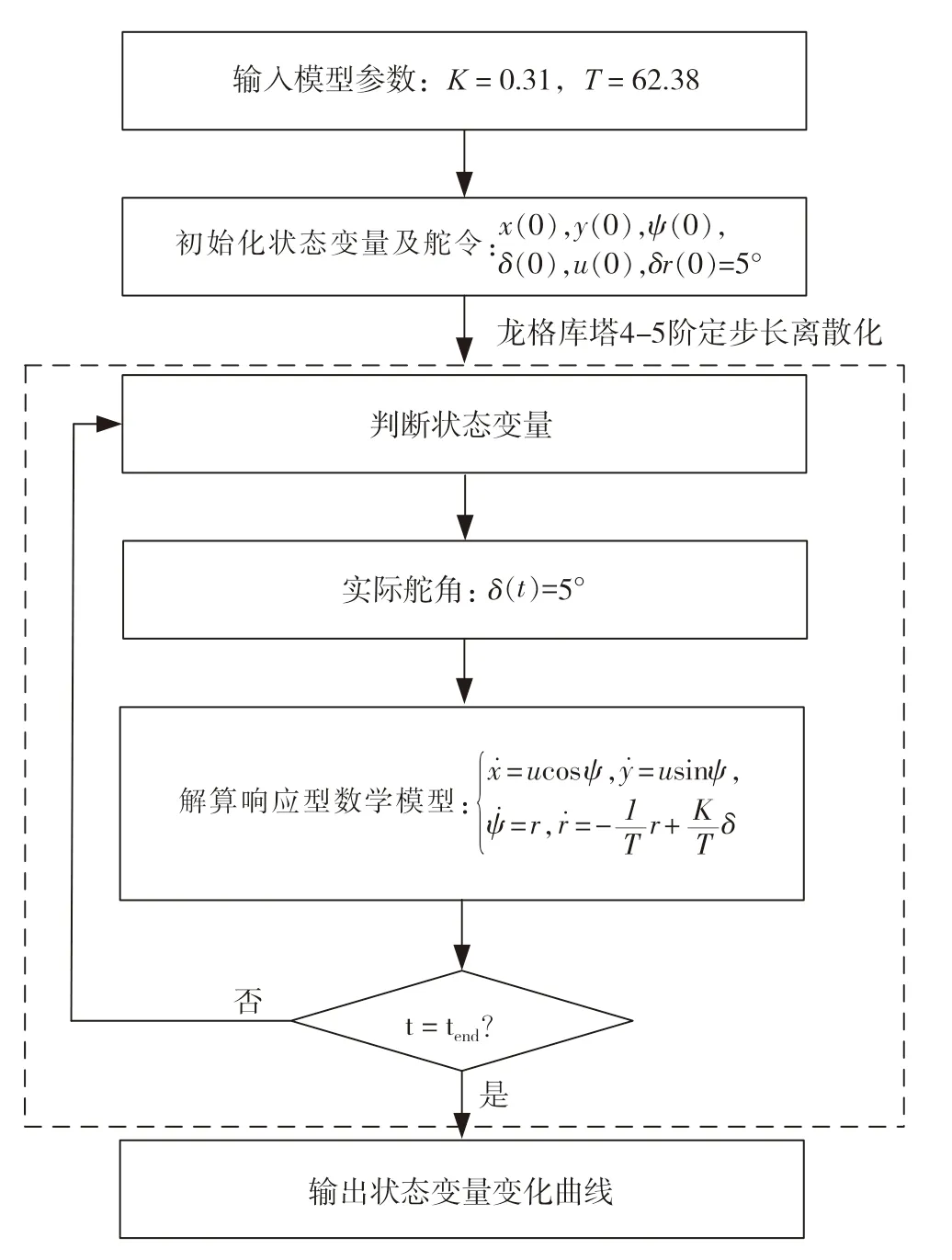
图7 旋回试验MATLAB仿真流程图

在船舶定速直航状态下，当转舵角

δ

= 5

°

时，图8、图9和图10给出了船舶旋回运动的仿真结果。从图8可以看出，航向

ψ

、

r

在200 s之内非线性增大，在200 s之后，船舶进入定常旋回阶段，航向匀速增大到360

°

，转艏角速度稳定在1.5

°

/s。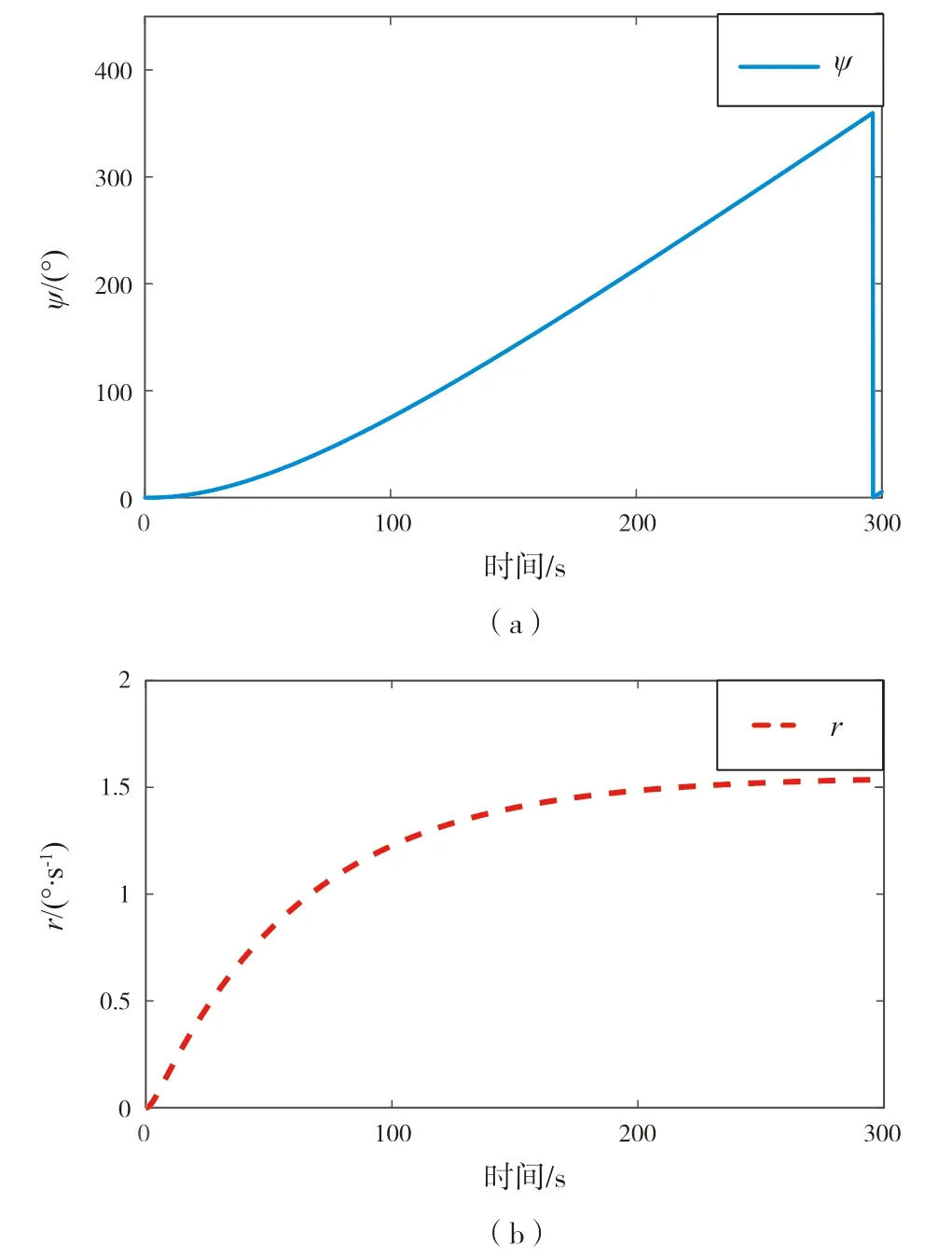

图8 旋回试验r，ψ-t仿真曲线

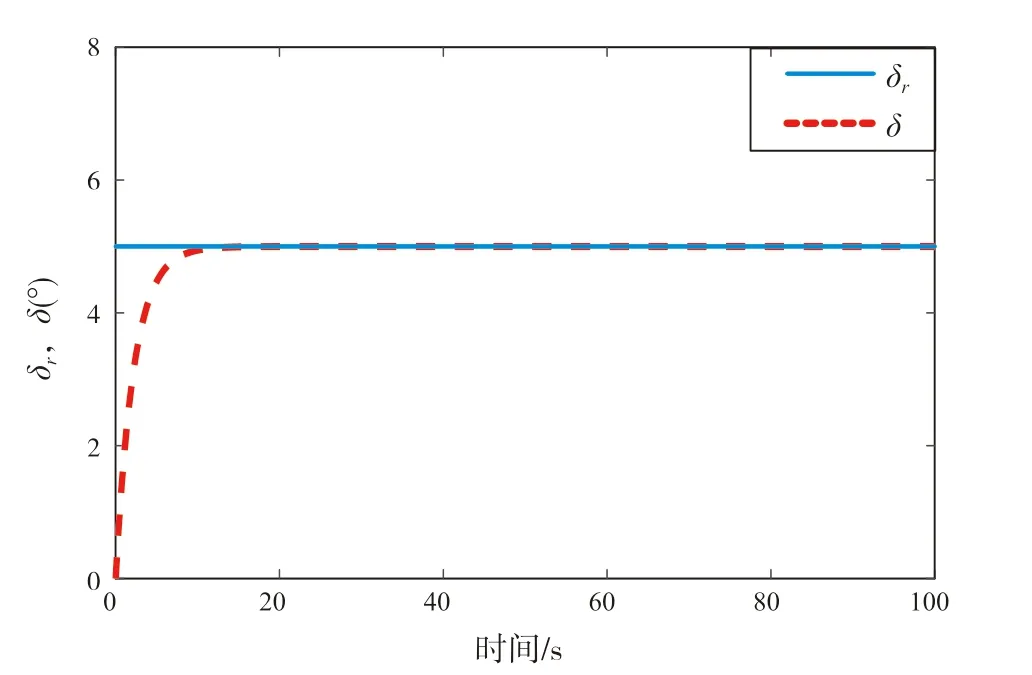
图9 旋回试验δr，δ-t仿真曲线

图9舵机伺服系统可以看出，命令舵角

δ

与实际舵角

δ

之间的关系：在初始一段时间内，实际舵角

δ

非线性增大；在15 s后，实际舵角

δ

与命令舵角

δ

达到一致。图10给出船舶旋回运动轨迹图。当命令右舷舵角5

°

时，船舶重心在纵轴方向发生移动，这段距离即图注

A

；此外，可见船舶旋回圈，而旋回圈直径（

D

）大小，将会反映定常旋回过程中占用水域的范围。由图10可见，旋回直径约是实际船长的5倍左右。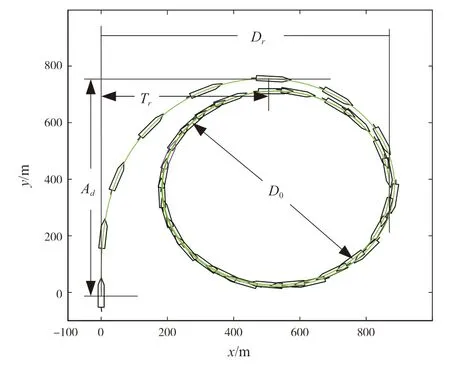

图10 旋回试验船舶运动仿真轨迹图

3 结 论

本文针对船舶旋回运动过程进行研究，分析了旋回过程中的3个阶段，并且针对旋回过程中的速降问题进行深入分析，利用速降估算公式对“OPALIA”轮压载状态下的左满舵与右满舵旋回速降进行预报，并与实际速降曲线进行对比，结果验证了速降估算公式的准确性。最后，在模拟海洋干扰环境下，采用龙格库塔4-5阶定步长离散化的方法，对“育鲲”轮进行MATLAB旋回仿真试验。仿真结果显示，旋回直径约为实际船长的5倍，这与实际工况相符，进一步说明了仿真试验的有效性与准确性。

本文尚存在以下不足：

（1） 船舶运动数学模型采用最简洁的Nomoto模型，该模型存在不足；

（2） 船舶旋回速降影响因素较多，没有确切的数学模型，因此，本文采用的速降估算公式尚存在一定误差。