基于改进正余弦优化神经网络的水体余氯预测
2021-04-27安小宇鲁奎豪崔光照赵复兴
安小宇 鲁奎豪 崔光照 赵复兴


摘 要:为保证居民用水安全,搭建更加准确、稳定的水质余氯预测模型,提出了一种改进正余弦算法优化神经网络的水体余氯预测模型。在正余弦算法(SCA)位置变化中加入非线性权重,平衡全局勘探和局部开发能力;同时在粒子更新后融入Levy飞行,丰富种群多样性,强化局部搜索能力;将改进正余弦算法用于BP神经网络参数优化,搭建ISCA-BP水体余氯预测模型。利用在线水质监测设备的监测数据进行余氯含量预测,不同预测模型结果对比表明,ISCA-BP模型预测结果相对误差的平均值为4.04%,均方根误差为0.011 3 mg/L,与BP、RBF神经网络模型相比,误差最小,模型预测结果与实际值最接近,泛化能力更强,预测结果精确度高,稳定性好。
关键词:余氯;ISCA-BP神经网络;正余弦算法;Levy飞行;非线性权重
中图分类号:TP183;X824 文献标志码:A
doi:10.3969/j.issn.1000-1379.2021.04.020
引用格式:安小宇,鲁奎豪,崔光照,等.基于改进正余弦优化神经网络的水体余氯预测[J].人民黄河,2021,43(4):111-116.
Abstract: In order to ensure the safety of residents water use, a more accurate and stable prediction model of residual chlorine in water quality was established. In this paper, an improved sine cosine algorithm was presented to optimize the prediction model of neural network. Add nonlinear weight to the position change of Sine Cosine Algorithm (SCA) to balance the global exploration and local development capability; at the same time, Levy flight was integrated after particle updating to enrich the diversity of the population and enhancing local search capabilities; then the improved sine and cosine algorithm was used for BP network parameter optimization to build the ISCA-BP prediction model. Finally, using the online water quality testing equipment for prediction of residual chlorine content and comparing different results of forecasting models, it found that the results of relative error of ISCA-BP model predicted is 4.04%, the average root mean square error is 0.011 3 mg/L, the error is lower than BP and RBF model. The prediction results of the model are the closest to the true value, the generalization ability of the ISCA-BP model is stronger, the accuracy of the prediction results is high and the stability is good.
Key words: residual chlorine; ISCA-BP neural network; sine and cosine algorithm; Levy flight; nonlinear weight
人口數量逐年递增、用水量日益增加使得用水量增加,与此同时人类生产和生活中污水排放导致水体污染、水质恶化,水资源更加紧张。供水公司通常利用二氧化氯杀死水体中的有害微生物达到消毒目的,在消毒的同时二氧化氯与水管壁上附着的生物膜发生反应,导致管网中因余氯含量降低而不能达到消毒目的。但余氯含量过高时,会对人体带来一定损害[1]。因此,通过预测余氯变化情况,精确控制加氯量,确保日常饮用水安全是当前研究的热点。谢昕等[2]运用RBF神经网络构建预测模型对余氯含量进行预测,但RBF神经网络参数选取较为困难,且模型预测精确度一般;王海霞等[3]利用多元线性回归方法得出了余氯含量与多个自变量的线性关系,构建了线性预测模型,但该模型存在数据不连贯等问题,使得余氯预测精确度下降;罗旭东等[4]通过在线水质监测设备实时采集数据,利用线性回归和非线性神经网络建立余氯预测模型,研究表明非线性神经网络模型的预测效果优于线性回归模型的;高爽[5]基于主成分分析法、遗传算法、BP神经网络提出了一种混合智能算法,通过遗传算法优化神经网络参数构建水质预测模型,从而提高模型的精确度;苏彩红等[6]利用改进人工蜂群算法优化神经网络水质预测模型,并对溶解氧含量进行了精确预测。
神经网络预测模型应用广泛,但存在收敛速度慢、易陷入局部最优、对初始权值和阈值敏感等问题,可将其与正余弦优化算法相结合,运用改进的正余弦算法优化神经网络预测模型对余氯含量进行预测。首先,将正余弦算法[7]位置变化中加入非线性权重,使算法达到全局探索与局部寻优的有效平衡;然后,在粒子位置更新后加入Levy飞行,提高种群的多样性,强化局部搜索能力,避免过早收敛情况出现,并采用6个基准测试函数对改进正余弦优化算法(ISCA)、粒子群优化算法(PSO)[8]、差分进化算法(DE)[9]、飞蛾扑火优化算法(MFO)[10]等的性能进行验证;最后,利用ISCA算法优化BP神经网络,建立ISCA-BP模型对水体中余氯含量进行预测,并将预测结果与RBF、BP神经网络模型预测结果进行对比,进一步验证该预测模型的性能。
1 供水信息化管理平台
为改进传统水质监测方式存在的過程烦琐、不具实时性、数据误差大等问题,设计了一种新型供水信息化管理平台。该平台依据实际需求将自来水公司管辖下的泵站、水源等重要供水单元纳入全方位监控与管理,运用物联网、云平台、大数据处理等技术构建包含数据实时采集系统、智能控制系统、数据传输和处理系统等的供水信息化管理平台,系统总体设计框架见图1。
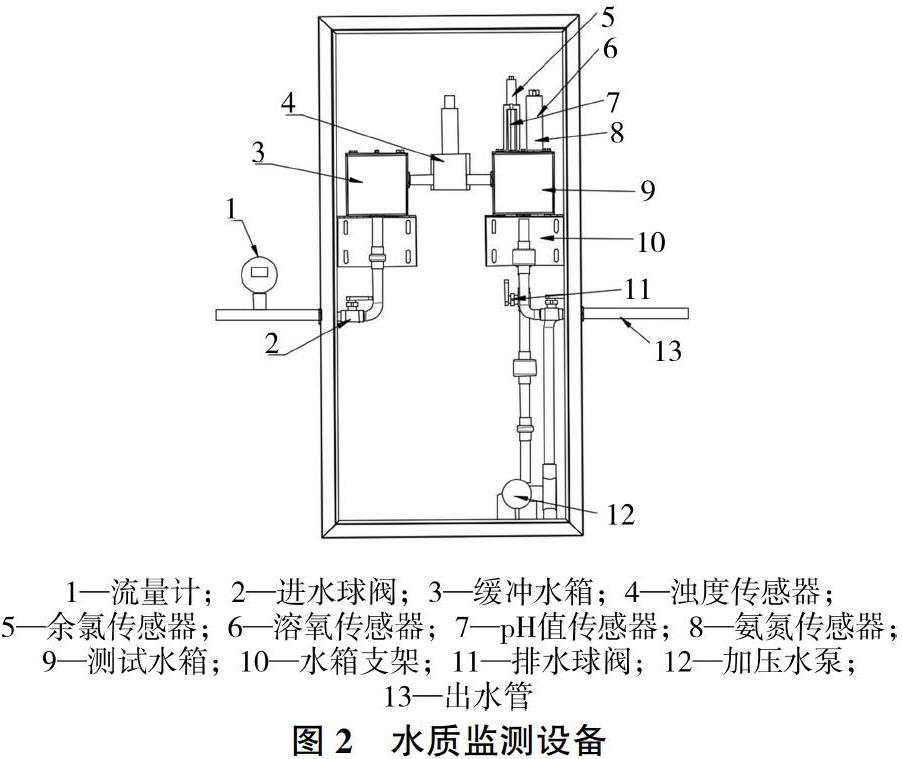
水质监测设备见图2,在线水质监测设备监测的数据主要包括余氯、pH值、温度等。通过水质在线监测系统实时传输数据,对水体中余氯含量进行预测,保障水体中二氧化氯的含量不小于0.05 mg/L。
2 余氯预测模型
2.1 标准正余弦算法
SCA算法是2015年Seyedali与Mirjalili提出的一种基于正弦余弦模型的优化算法[7],该算法以一组随机解开始,通过在目标函数下不断勘探和开发提高算法的精确度,其位置更新公式为
SCA算法具有局部开发和全局勘探能力。当函数的返回值在-1~1时,种群会在期望的搜索空间寻优;当函数返回值在-1~1之外时,种群将在更远的空间勘探。
2.2 改进正余弦算法
(1)非线性权重。针对SCA算法存在的后期局部开发能力弱、收敛精确度不高、收敛速度慢问题,加入非线性权重对SCA算法进行改进,较大的权重有利于提高算法的全局勘探能力,而较小的权重可以提高算法在目标值附近的寻优能力,能够更好平衡算法的全局勘探和局部开发能力。非线性权重ω为
(2)基于Levy飞行改进SCA算法。Levy飞行是一种描绘随机步长的方法,其探索过程长时间短距离与偶尔长距离的移动方式随机切换,保证算法的探索能力,丰富种群的多样性,加强跳出局部极小值的能力,防止出现过早收敛的情况,其计算公式为
基于Levy飞行改进SCA算法使得算法实现搜索域的多样化,更加高效探索目标位置,从而取得更好的寻优结果。
2.3 ISCA-BP预测模型
神经网络训练成果与初始权值、阈值有关,随机选取初始值时,训练周期长、稳定性差、预测性能差[11-12]。针对这些问题,采用ISCA算法优化神经网络初始状态权值、阈值[13-15],构建余氯含量预测模型。模型建立步骤如下。
步骤1:参数初始化。种群粒子数为N,粒子维数为D,输入层节点数为M,隐含层节点数为q,输出层节点数为1,BP网络结构为M-q-1,则空间维数为
步骤2:数据处理。将样本数据进行归一化处理并分类。
步骤3:确定适应度函数。选取式(8)作为适应度函数,当函数值满足设定值时为最优解。
步骤4:粒子初始位置、初始权值和阈值的初始化。
步骤5:通过式(8)计算适应度值,确定正余弦算法初始时刻适应度值。
步骤6:粒子位置更新。利用改进后的位置更新式(6),对粒子的位置进行更新。
步骤7:计算适应度值。对更新后粒子的适应度值进行计算,对比当前粒子与之前最优粒子的适应度值,将两者中适应度值最优的视为最优解。
步骤8:重复步骤6、步骤7,直到适应度函数值达到标准或者满足最大迭代次数,此时的结果为全局最优解。
步骤9:将最优的权值、阈值代入BP神经网络得到余氯含量预测模型。
3 仿真试验
3.1 ISCA算法性能测试
选取6种基准测试函数[7]验证ISCA算法的收敛性能,基准测试函数见表1,其中F1、F2、F3为单峰测试函数,F4、F5、F6为多峰测试函数。比较ISCA算法与PSO算法、MFO算法、DE算法、SCA算法的收敛效果,并观察其收敛曲线、平均值和标准差。
为了对比5种算法的收敛效果,设置5种算法的参数:种群大小为30,维数为30,迭代次数为500;ISCA算法中非线性权重的最大权重为0.8,最小权重为0.000 4;DE算法中比例因子为0.5,交叉常数为0.2;PSO算法中学习因子ca=2、cb=2。从收敛精确度和收敛速度对5种算法的结果进行评价,结果见图3。
从图3可以看出,无论是单峰函数还是多峰函数,相对于其余4种算法,ISCA算法收敛精确度更高、收敛速度更快。为进一步验证试验的准确性,每种算法在基准测试函数下进行30次试验,其最优解的平均值、标准差见表2。
从表2可以看出,对于测试函数F1、F2、F3、F4、F6,ISCA算法能够找到其理论最优结果,对于测试函数F5,ISCA算法相较于其他4种算法精确度最高。进一步说明,相较于其余4种算法,ISCA算法收敛速度快、收敛精确度高、稳定性强,是一种综合性能较强的算法,适用于余氯预测模型的参数优化。
3.2 余氯预测试验
管道中影响余氯含量的因素很多,包括季节、温度、pH值、浊度、溶氧含量等。温度升高将促进余氯与水中相关物质发生化学反应,从而加快氯的消耗,而且温度升高将加快水中微生物的生长与繁殖,增加二氧化氯的消耗,所以温度越高氯消耗越多;氯与水相溶生成盐酸与次氯酸,次氯酸分解为H+与OCl-,当pH值大于7.5时,次氯酸根含量较高,当pH值小于7.5时次氯酸含量较高,所以当pH值较高时水体中余氯含量较高;水的浊度不仅与水体中悬浮物的含量有关,而且与悬浮物的大小、形状及折射系数等有关,颗粒状物质会带来大量营养物质促进微生物生长,浊度越高微生物含量越多,对消毒剂的需求越大,使得余氯含量降低;溶氧含量对余氯含量影响较小,但是溶解氧含量是水体污染情况的反映。随机选取60组平顶山某地区水厂5月的温度、pH值、浊度、溶氧含量进行试验,水体采样数据见表3。对采样数据进行归一化处理,将其中50组数据作为训练样本,10组数据作为测试样本。
ISCA算法参数设置:种群大小为30,维数为73,输入层节点數为4,输出层节点数为1,隐含层节点数为12。其中,隐含层的选择通过对比训练样本在不同隐含层下的训练误差得到,隐含层节点数为3、4、…、13时,训练误差分别为0.793 2、0.725 7、0.479 1、0.127 0、0.217 9、0.031 2、0.021 0、0.022 3、0.022 0、0.020 2、0.021 6 mg/L,当隐含层为12时训练误差最小,因此取隐含层节点数为12。
ISCA-BP模型训练样本预测值与实际值对比见图4,可以看出对于训练样本ISCA-BP模型能够准确拟合。由图5可知,对于测试样本BP、RBF神经网络模型余氯含量预测曲线与实际曲线偏差较大,ISCA-BP模型余氯含量预测曲线的拟合精确度更高,说明其具有较强的泛化能力。测试样本预测误差曲线见图6,由图6可以看出,与BP、RBF神经网络模型相比,ISCA-BP模型曲线更加平稳,更接近于0,说明其预测精确度更高。
为了更好体现ISCA-BP预测模型的性能,通过绝对误差的平均值、相对误差的平均值、均方根误差3个指标来评价预测结果,见表4。从表4可知,ISCA-BP预测模型绝对误差平均值为0.008 1 mg/L,相对误差平均值为4.04%,均方根误差为0.011 3 mg/L,与其他两种模型相比,数值最小,表明其预测结果与实际值最接近,模型预测精确度高,稳定性好。进一步证明了ISCA-BP预测模型具有更强的泛化能力和更高的预测精确度。
4 结 论
通过在线水质监测设备对饮用水进行实时监测,利用温度、pH值、浊度、溶氧等监测数据对水体中余氯含量进行预测,从而控制加氯设备运行,保证水体中余氯含量不小于0.05 mg/L。6种标准测试函数对ISCA算法、PSO算法、MFO算法、DE算法、SCA算法进行对比试验表明,ISCA算法是一种优化性能更强的算法。在此基础上建立ISCA-BP余氯预测模型,与BP、RBF神经网络模型相比,该模型预测结果的绝对误差、相对误差、均方根误差最小,表明ISCA-BP模型具有更强的泛化能力和更高的预测精确度。
参考文献:
[1] 唐洋.配水管网余氯及DOM分布变化规律与余氯预测研究[D].西安:西安理工大学,2018:2-3.
[2] 谢昕,郭鹏飞,詹小丽.基于RBF神经网络的余氯浓度预测模型研究[J].传感器与微系统,2012,31(8):64-65,68.
[3] 王海霞,张信阳.供水管网余氯预测的研究[J].天津工业大学学报,2003,22(6):34-36.
[4] 罗旭东,廖静.城市给水管网余氯的预测模型[J].城市环境与城市生态,2006,19(1):11-13.
[5] 高爽.主成分分析-BP神经网络法在漳河水质评价中的联合应用[D].邯郸:河北工程大学,2018:5-6.
[6] 苏彩红,向娜,林梅金.基于ABC优化算法的神经网络水溶解氧预测[J].计算机仿真,2013,30(11):325-329.
[7] MIRJALILI S. SCA: A Sine Cosine Algorithm for Solving Optimization Problems[J]. Knowledge-Based Systems, 2016(96): 120-133.
[8] KENNEDY J, EBERHART R C. Particle Swarm Optimization[C]//IEEE.Proceedings of IEEE International Conference on Neural Networks. Perth: IEEE, 1995: 1942-1948.
[9] STORN R, PRICE K. Differential Evolution: a Simple and Efficient Heuristic for Global Optimization over Continuous Spaces[J].Journal of Global Optimization, 1997, 11(4): 341-359.
[10] MIRJALILI S. Moth-Flame Optimization Algorithm: a Novel Nature-Inspired Heuristic Paradigm[J]. Knowledge-Based Systems, 2015,89: 228-249.
[11] 赵振国,刘丽,徐建新.基于BP神经网络预测区域农业用水量[J].人民黄河,2007,29(9):59-60,62.
[12] 杨永宇,尹亮,刘畅,等.基于灰关联和BP神经网络法评价黑河流域水质[J].人民黄河,2017,39(6):58-62.
[13] 龙盼.基于优化BP神经网络的油田回注水余氯预测模型研究[D].武汉:武汉科技大学,2016:28-29.
[14] 桑宇婷,赵雪花,祝雪萍,等.基于CEEMD-BP模型的汾河上游月径流预测[J].人民黄河,2019,41(8):1-5.
[15] 卜松,王军,郭力文.ACA-BP网络在冰塞水位预测中的应用[J].人民黄河,2009,31(5):45-47.
【责任编辑 吕艳梅】
