山区双车道公路摩托车事故黑点及致因集成分析
2021-04-27戢晓峰邓宇泽杨文臣覃文文普永明
戢晓峰,邓宇泽,杨文臣,覃文文,普永明
(1. 昆明理工大学 交通工程学院, 云南 昆明 650500; 2. 昆明理工大学 云南省现代物流工程研究中心,云南 昆明 650504; 3. 云南省交通规划设计研究院 陆地交通气象灾害防治技术国家工程实验室,云南 昆明 650200)
0 引 言
目前,在我国山区双车道公路途径的农村地区,摩托车是当地农村居民的主要出行方式.由于山区公路线形复杂,造成摩托车事故频发[1].统计发现,山区双车道公路的交通事故发生率占全部公路的15%以上,而摩托车事故更是占据山区双车道公路事故的主导地位[2].因此,针对摩托车进行事故黑点鉴别与致因分析,已经成为山区公路事故治理的迫切需求.
近年来,山区公路交通安全逐渐成为研究热点,但多以全路段为研究单元,如戢晓峰等[3]基于事故数据探讨了事故致因的时间演化机制,鲜有研究考虑山区公路对摩托车事故的影响.摩托车事故研究早期以分析碰撞机理、提出驾驶员保护措施为主[4-5],逐步涉及摩托车事故的影响因素及伤害程度评估,如Xiong等[6]建立了摩托车驾驶员受伤严重程度的Logistic回归模型,发现了增加摩托车驾驶员重伤可能性的影响因素;Chang等[7]获取了摩托车驾驶员伤害严重程度的影响因素;Alexander等[8]以美国俄亥俄州摩托车事故为基础,建立混合Logit模型发现了与事故伤害程度相关的主要因素;温惠英等[9]利用美国印第安纳州摩托车数据,分别建立Nested Logit与Random Parameters Logit模型分析了摩托车事故伤害严重程度的因素.然而,由于山区双车道公路的运行环境及交通流特征较为特殊,现有相关研究成果无法直接应用.为科学治理山区双车道公路摩托车事故,急需开展摩托车事故黑点鉴别与事故致因集成分析.现有事故黑点鉴别方法多将研究路段以固定的步长进行划分,一方面会夸大或遗漏事故黑点,另一方面现阶段事故黑点鉴别未能与事故致因集成分析,尚未形成系统化的山区摩托车事故黑点治理方法.
综上,本文针对山区双车道公路的事故治理实际需要,提出摩托车事故黑点鉴别及致因集成分析方法,研究结果对山区双车道公路交通安全具有现实意义.
1 集成分析流程
1.1 山区双车道公路摩托车事故黑点鉴别
1)数据采集.采集山区双车道公路的线形数据及摩托车事故数据.线形数据包括起点桩号、终点桩号、路段长度、平曲线类型、平曲线半径、平曲线偏角、竖曲线类型、竖曲线半径、纵坡坡度等.
2)确定基本单元及步长.首先,需划分路段单元,选择1 km作为基本单元[10];其次,确定移动步长,选用200 m、300 m、400 m、500 m四种步长分别对路段进行划分,如图1所示,通过比较事故密度选取适用于研究路段的最佳移动步长.在确定路段单元步长的基础上,输入摩托车事故数据,将其匹配到路段,并按路段单元和移动步长划分路段.

图1 移动步长法Fig.1 Moving step method
3)初选事故黑点提取.输入摩托车事故数据,考虑其严重程度,借鉴当量事故法赋予事故次数、死亡人数、受伤人数、财产损失四个指标相应的权值,输出当量事故数据,如式(1)所示:
ETAN=αF+βJ+γC+TAN
(1)
式中: ETAN为当量事故数,F为死亡人数,J为受伤人数,C为事故财产损失数,TAN为发生的事故次数,α为事故死亡权重,β为事故受伤权重,γ为财产损失权重.参考国内外研究[11],设定死亡权重为2.0,受伤权重为1.5,财产损失权重为1.0,即α=2.0,β=1.5,γ=1.0.
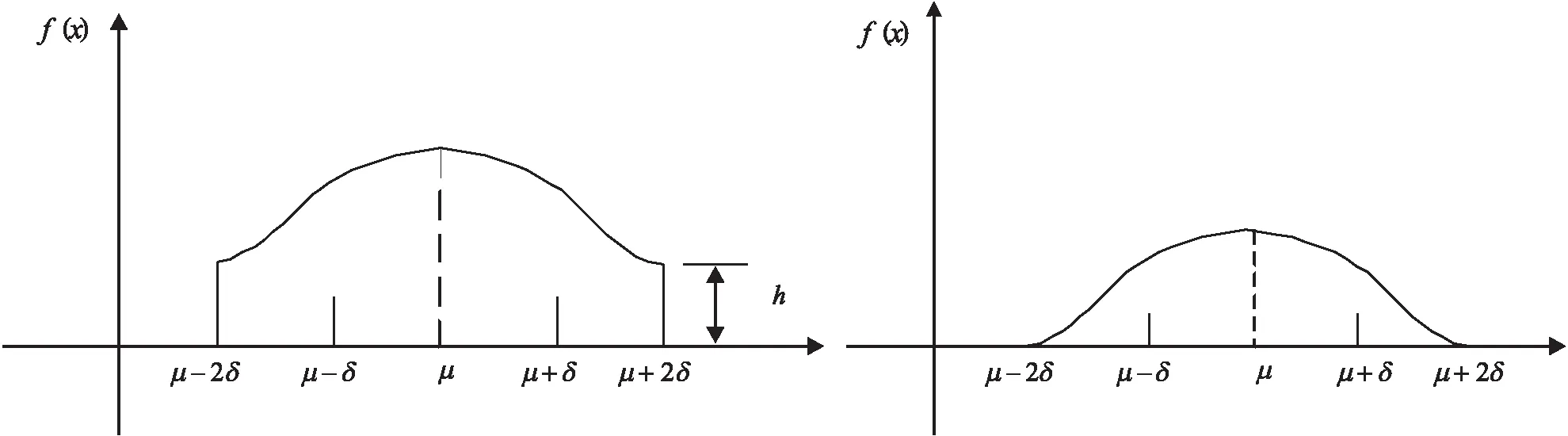
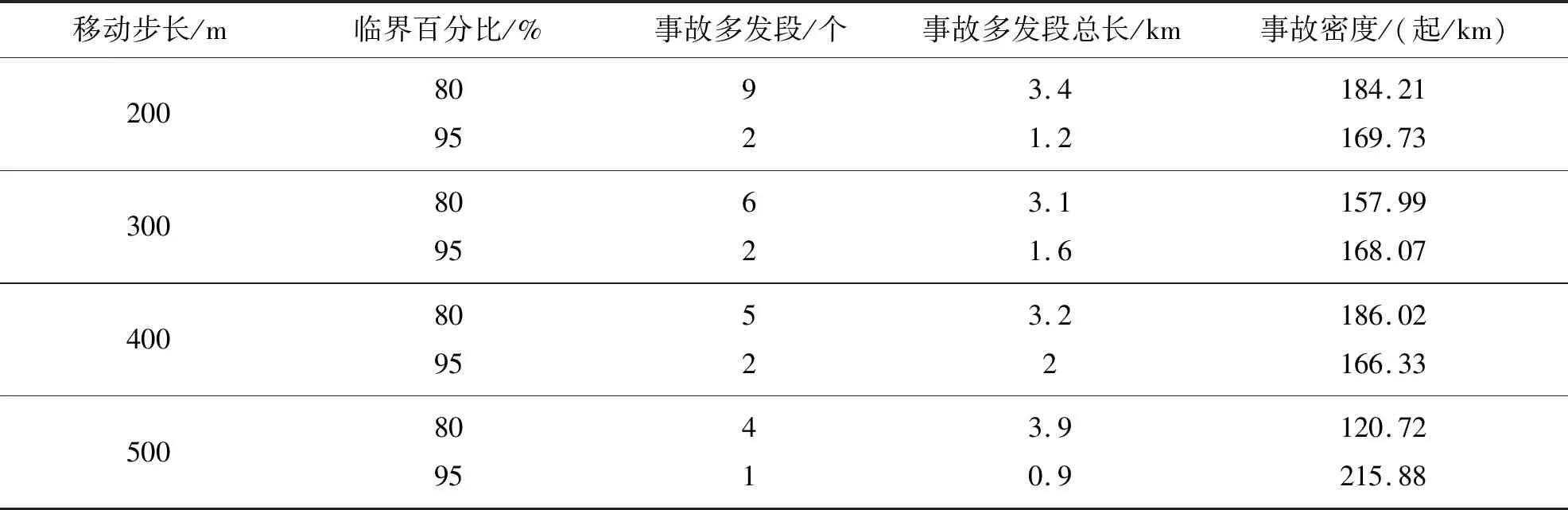
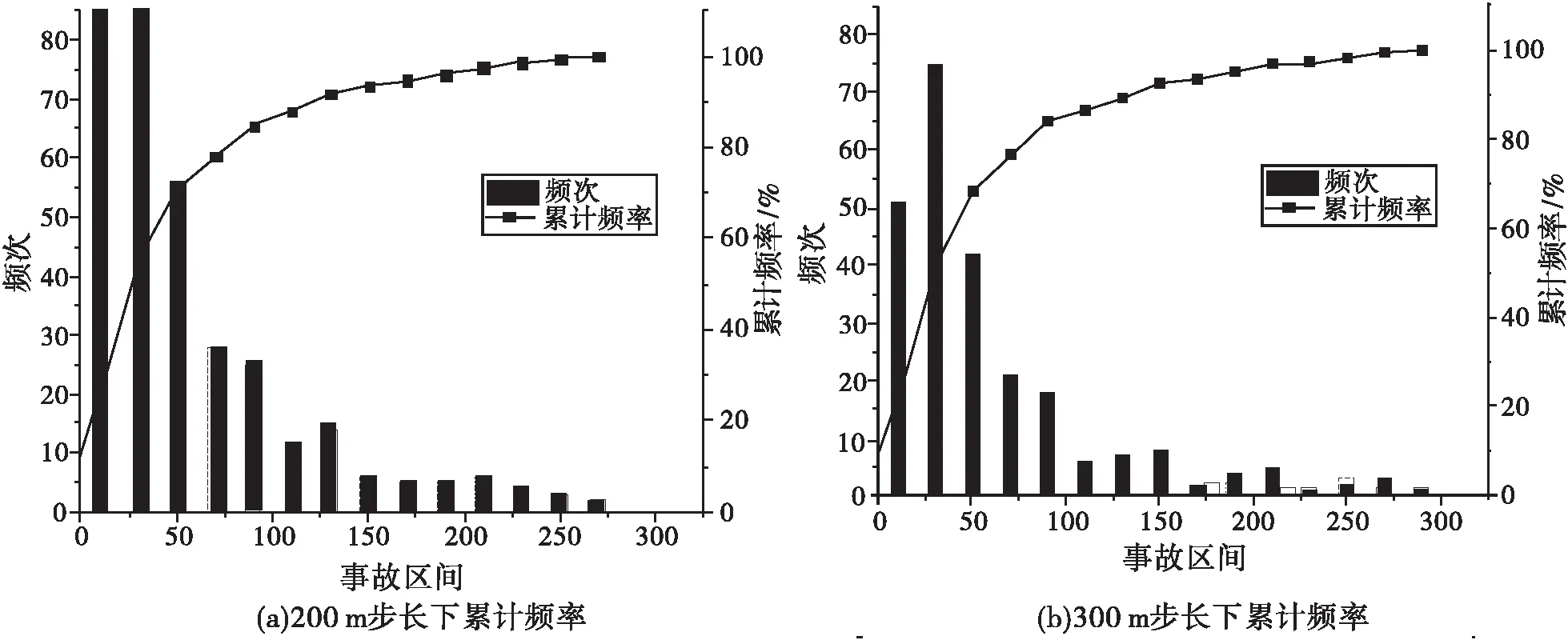
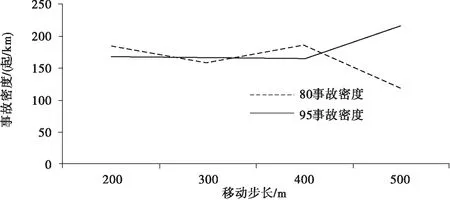
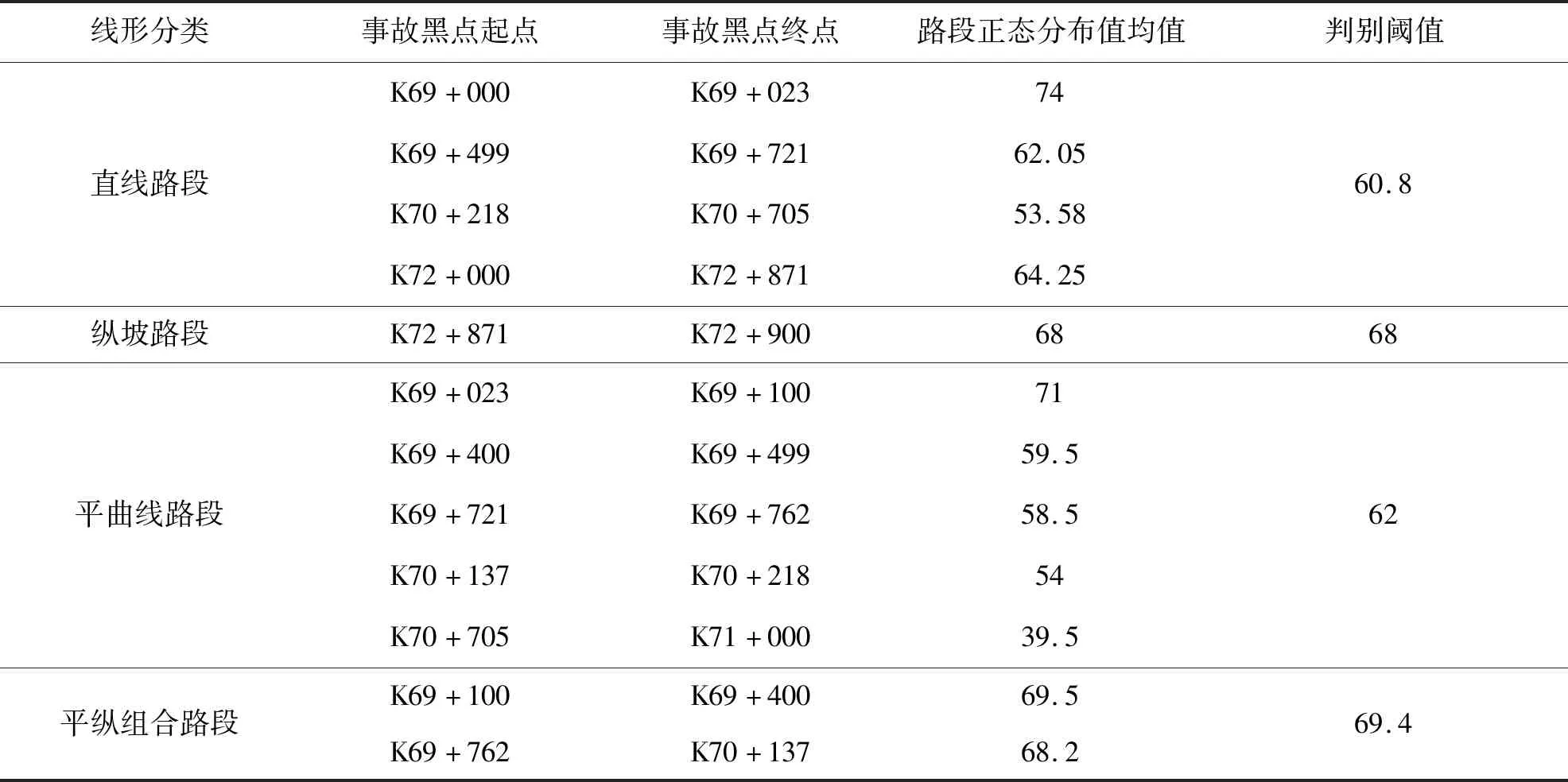
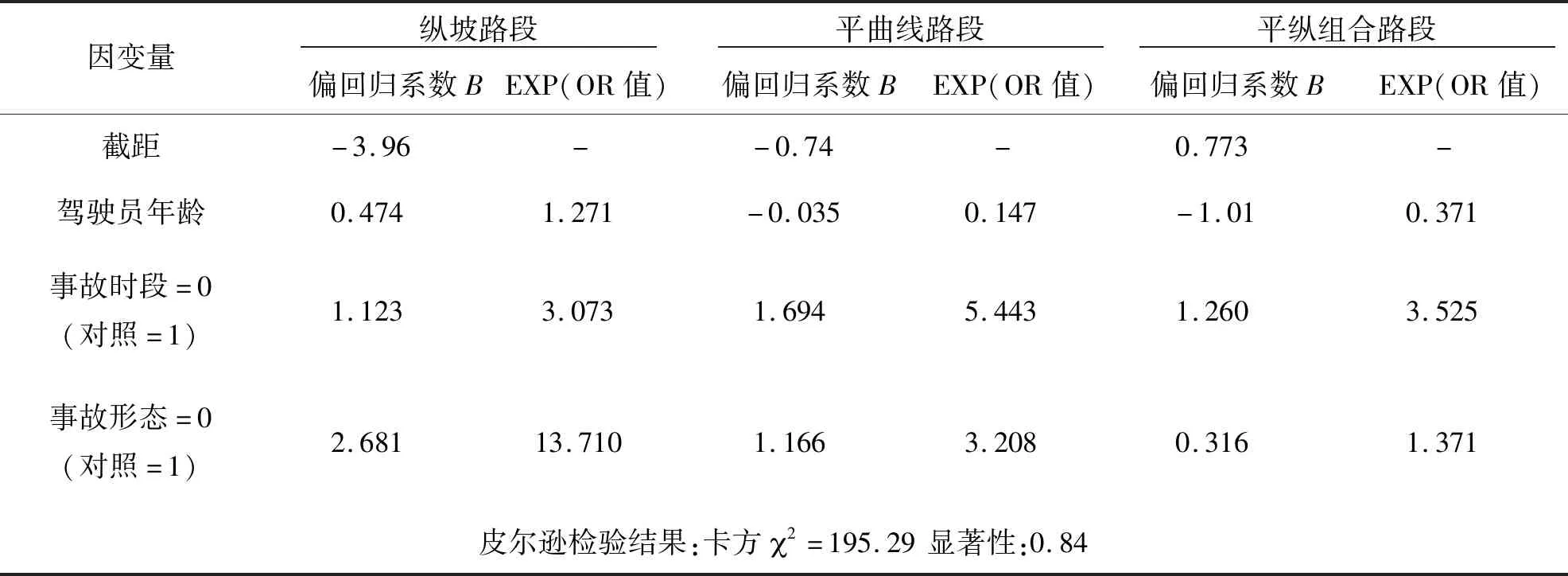
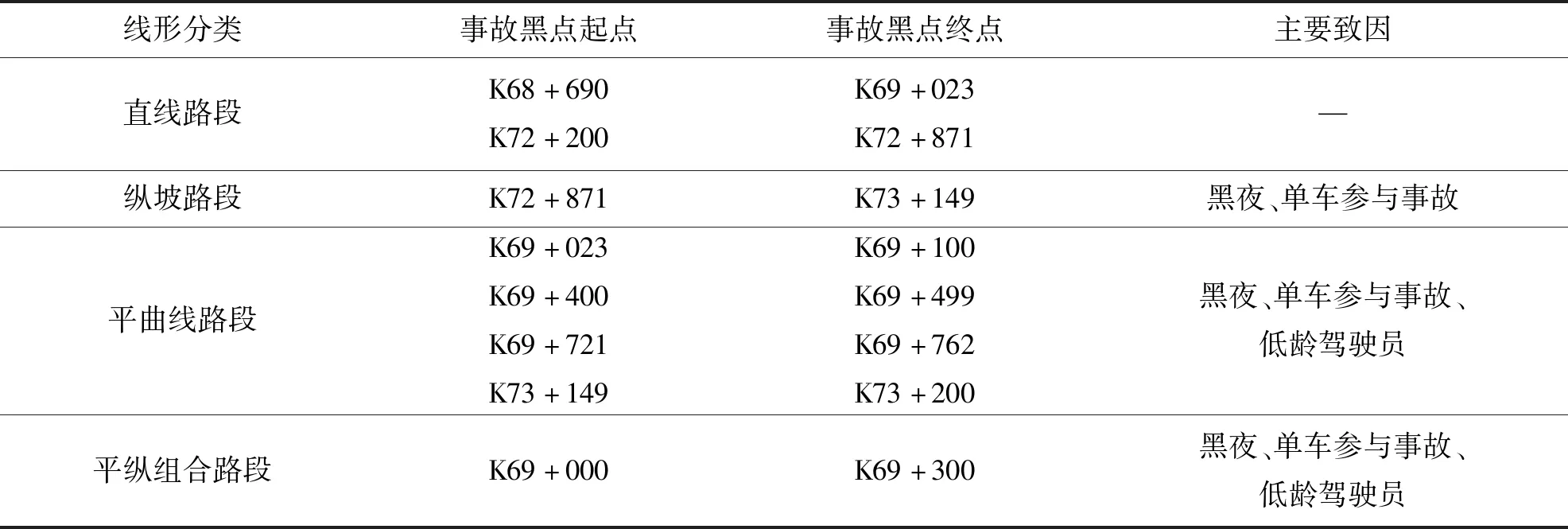
考虑到传统事故黑点鉴别方法的局限性,将当量事故法与累计频率法相结合,选择当量事故数据,拟合累计频率散点图,突变点即为初选事故黑点.定义当量事故数为N,将事故累计频率大于80%和95%的当量事故数N80、N95作为临界值,如图2所示.其中,在N>N95范围内对应的路段为事故多发点,在N95>N>N80范围内对应的路段为潜在事故多发点,在N 图2 累计频率法Fig.2 Cumulative frequency method 4)初选路段线形分类.山区双车道公路线形复杂,需在事故黑点初选的基础上,针对线形开展事故黑点精确识别.根据初选事故黑点,依据纵坡坡度和平曲线半径将其划分为直线路段、纵坡路段、平曲线路段和平纵组合路段四类[12],如表1所示. 表1 路段划分标准Tab.1 Division criteria 5)引入并改进正态分布曲线模型.事故黑点由多个事故地点组成,为精确识别事故黑点,需定量分析事故地点严重程度,故引入正态分布曲线模型. 正态分布曲线是一条向两端无限延伸的曲线,为便于黑点精确识别,需对其改进.区间[μ-2σ,μ+2σ]的概率为0.95,已符合交通工程的要求,故可忽略两侧数值较小部分.然而,边界部分的函数值突变成0,不符合事实规律.为进一步优化模型,将曲线整体下降h,h为标准函数位于2σ的数值,示意图如图3所示.改进正态分布曲线模型f1(x)如式(2)~式(3)所示: (2) (3) 式中:μ代表了自变量x的均值,σ代表了正态分布曲线的标准差.由于基本单元选为1 km,为保持一致标准,选择1 km为正态分布曲线的自变量范围,即4σ=1,σ取1/4. (a)正态分布曲线改进前示意图 (b)正态分布曲线改进后示意图图3 改进正态分布曲线模型Fig.3 Improved normal distribution curve model 为更好地对自变量的危险性进行区分,选定当量事故法为依据,输入摩托车事故数据,将当量事故数赋予标准函数进而输出正态分布值,修正后的正态分布曲线模型f2(x)如式(4)所示: (4) 式中:L代表事故地点,xL代表事故地点横坐标,FL、JL、CL、TANL分别为该点的死亡人数、受伤人数、事故财产损失数及事故数. 6)确定事故黑点判别阈值.首先,以初选路段线形分类结果为研究单元,计算同一路段全部事故地点的正态分布值并均值处理,然后将同一种线形的不同路段按当量事故数进行加权计算,得到特征量作为每种线形路段的事故黑点判别阈值. 7)精确识别事故黑点提取及排序.输入全路段正态分布值,将路段事故危险性以曲线形式表示,考虑到事故的扩散性及事故地点间的相互影响,故对所有曲线重叠部分进行叠加,通过对曲线的拓展,最终得到全路段正态分布曲线. 以获取的山区双车道公路摩托车事故黑点为研究对象,构建无序多分类Logistic回归模型. 1)自变量选取.从人、车、路、环境四方面选取山区双车道公路摩托车事故的潜在影响因素为自变量.为保证模型的可靠性,需筛选与因变量显著相关的自变量,剔除ρ>0.1的变量,最终进入似然比检验的变量均较为显著. 2)构建无序多分类Logistic模型.在鉴别各类线形事故黑点的基础上,需对摩托车事故主要诱因进行辨析.由于因变量类别为四类,且类别间无次序关系,引入无序多分类Logistic回归分析因变量与自变量间的关系,基于山区双车道公路摩托车事故特性,以直线路段为参照,分别与纵坡路段事故、平曲线路段事故、平纵组合路段事故构建三个广义Logistic回归模型,提取影响事故的潜在因素作为输入变量,构建山区双车道公路摩托车事故致因分析模型,输出不同线形路段事故黑点致因,如式(5)~式(7)所示,并通过拟合优度检验及准确度检验验证模型是否成立: (5) (6) (7) 式中,y1、y2、y3、y4为因变量发生概率.某自变量的偏回归系数β的自然指数eβ表示该变量增加一个单位时,因变量取值水平发生的概率增加eβ倍.具体来说,偏回归系数为正,表明事故易在纵坡路段、平曲线路段、平纵组合路段三个路段发生;偏回归系数为负,表明事故易在直线段发生. 选取典型的山区双车道公路云南省楚雄州元双公路为研究对象,开展事故资料收集和交通调查工作.截至2018年底,楚雄州摩托车拥有量达43.12万辆,每百人摩托车拥有量高达15.67辆,摩托车已经成为当地重要的出行方式.元双公路全长78 km,设计速度60 km/h.摩托车约占交通流的20%左右,且行车环境较复杂,其平曲线最小半径为200 m,最大纵坡为6%.采集2011—2017年摩托车事故数据,数据字段包括事故编号、案情摘要、事故地点、死亡人数、失踪人数、受伤人数、直接财产损失、天气、路表路面情况、事故形态、照明条件、涉事车辆等. 将摩托车事故次数当量处理,计算不同步长取值情况下的累计频率.采用80%和95%两个判别临界百分比对路段进行黑点鉴别,计算移动步长为200 m、300 m、400 m、500 m时的累计频率,如图4所示. 图4 不同步长累计频率曲线Fig.4 Asynchronous long cumulative frequency curve 统计并整合不同步长的黑点、黑点总长、事故密度三项指标,刻画移动步长与事故密度的关系,如表2、图5所示. 表2 初选事故黑点指标统计Tab.2 Statistics of black spots in primary election accidents 图5 移动步长与事故密度关系Fig.5 Relationship between moving step size and accident density 分析摩托车事故初选黑点可知,随着移动步长增加,事故多发段的事故密度整体呈平稳趋势,其中500 m步长下事故密度最大,路段总长呈现减少趋势;潜在事故多发段事故密度整体呈下降趋势,其中400 m步长下事故密度最大,路段总长呈平稳趋势.因此,事故多发路段选用500 m作为移动步长,潜在事故多发段选用400 m作为移动步长.整理分析可知,事故多发段为K69+600~K70+500,累计0.9 km,占研究里程的1.2%,事故数占研究事故总数的6.4%;潜在事故多发段为K69+000~K71+000、K72+000~K72+900,累计3.2 km,占4.38%,事故数占21.92%. 在事故黑点初选的基础上,依据表1对初选事故黑点按线形划分为12段,以此确定各类线形路段的事故黑点判别阈值.以K69+000~K69+023.64段为例,得到此段12次事故的正态分布值均值,并将直线路段的四路段均值按当量事故数加权,得到直线路段的事故黑点判别阈值,如表3所示. 表3 各类线形路段黑点判别阈值Tab.3 Threshold for each segment of black spot 通过比较各类线形路段的事故黑点判别阈值,发现曲线路段黑点的危险性整体高于直线路段黑点,有坡路段黑点危险性整体高于无坡路段黑点.整合全段路所有事故点及当量事故值,通过对不同事故点正态分布曲线进行叠加,得到全路段正态分布曲线,如图6所示,并以每种线形黑点判别阈值为基准筛选黑点.筛选过程以直线段为例,参考表3,已知直线段判别阈值为60.8,首先筛选全路段中危险指数大于60.8的路段,再挑选出其中的直线路段确定为直线段事故黑点;同理,提取其他线形路段事故黑点.综上,元双公路获取精确识别摩托车事故黑点8段,共计2.8 km,并按特征量对精确识别事故黑点进行排序,如表4所示. 表4 各类线形路段事故黑点统计Tab.4 Statistics of accident black spots on various linear sections 图6 事故黑点精确识别Fig.6 Precise identification of accident black spots 2.2.1 变量选取 依据元双公路运营特征[13],筛选调研数据,选取天气、事故发生时段、事故形态、是否涉及大客车和大货车、驾驶员性别、违章类型、驾驶员年龄七项典型因素为自变量,其中年龄为连续变量,其余为类别变量.将它们选择为对照组,自变量编码如表5所示. 表5 自变量的取值与编码Tab.5 Value and encoding of independent variables 2.2.2 结果分析 为保证模型可靠性,筛选与因变量显著相关的自变量,剔除ρ>0.1的变量,最终进入似然比检验的变量均较为显著.经筛选,得到整体显著的变量有驾驶员年龄、事故时段和事故形态.似然比结果显示,事故时段在0.01水平上显著,驾驶员年龄和事故形态在0.05水平上显著,回归结果如表6所示. 表6 模型回归结果Tab.6 Model regression results 模型整体在0.01水平上显著,模型正确百分比为85.0%,模型拟合效果较好、准确度较高.以直线段为参照分别建立无序多分类Logistic模型,公式如式(8)~式(10)所示: (8) (9) (10) 基于模型分析,将各因素结合获取事故黑点,得到各类线形路段黑点的主要致因,纵坡路段黑点主要致因为黑夜、单车参与事故;平曲线路段和平纵组合路段黑点主要致因为黑夜、单车参与事故、低龄驾驶员,如表7所示. 表7 各类线形路段事故黑点主要致因Tab.7 Inducing factors of black spots in various linear road accidents 1)本文集成移动步长结合累计频率法、正态分布模型、无序多分类Logistic模型,构建了山区双车道公路摩托车事故黑点鉴别及致因集成分析方法,尝试建立山区双车道公路摩托车事故治理的系统化流程.通过元双公路进行实例分析,该方法适用于山区双车道公路,获取了摩托车事故黑点及主要致因. 2)元双公路摩托车事故初选黑点12段,共3.2 km,精确识别黑点8段,共2.8 km.曲线路段的危险性整体高于直线路段,有坡路段危险性整体高于无坡路段.直线路段、纵坡路段、平曲线路段和平纵组合路段事故黑点判别阈值分别为60.8、68、62、69.3. 3)驾驶员年龄、事故时段和事故形态与各类线形路段的黑点事故相关性较高.纵坡路段事故黑点的主要诱发因素为黑夜、单车参与事故;平曲线路段和平纵组合路段事故黑点的主要诱发因素为黑夜、单车参与事故、低龄驾驶员.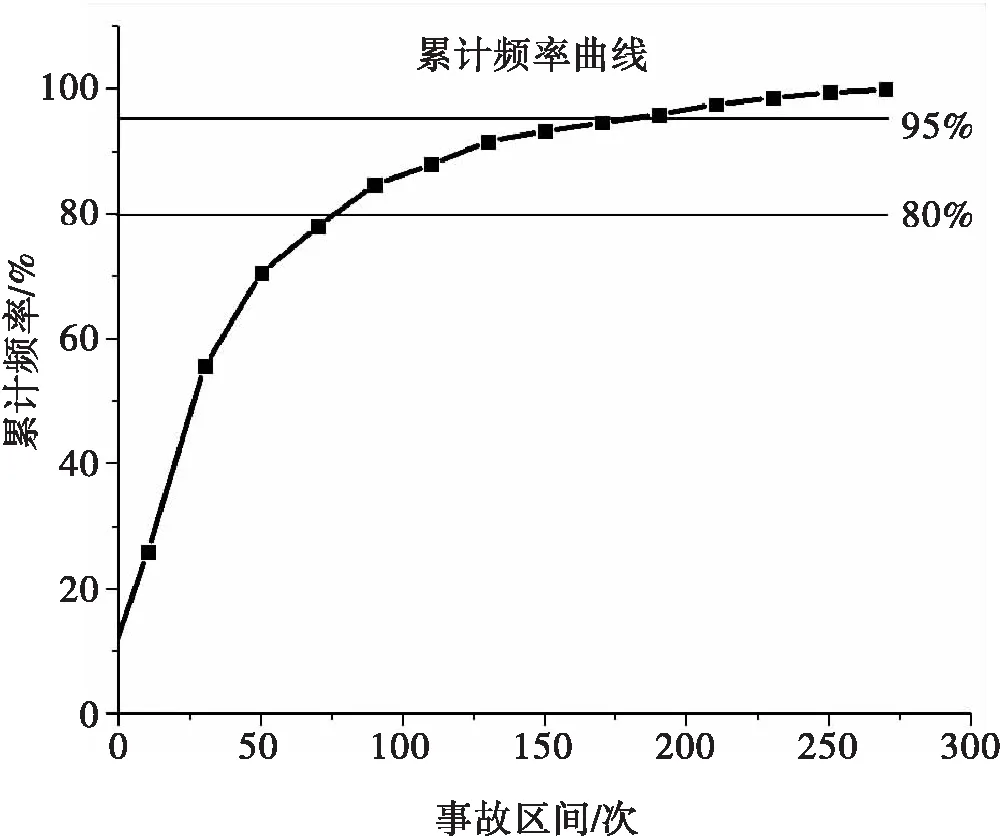

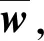
1.2 摩托车事故黑点路段的事故致因分析
2 实例分析
2.1 山区双车道公路摩托车事故黑点鉴别



2.2 摩托车事故黑点路段事故致因集成分析

3 结论
