基于多变量时间序列及向量自回归机器学习模型的水驱油藏产量预测方法
2021-04-27张瑞贾虎
张瑞,贾虎
(“油气藏地质及开发工程”国家重点实验室 西南石油大学,成都 610500)
0 引言
近年来,随着人工智能技术在石油工业领域的应用与推广,油田进入信息化、智能化时代[1-2]。油田开发的各个环节都积累了大量的历史生产数据,且数据形式多样、结构复杂,传统的分析预测方法已经无法满足需求,因此,需要发展一种智能化生产数据分析预测方法。
合理地引入人工智能方法,建立适应于油田数据的机器学习模型,是进行油田数据智能分析的关键。2004年Li等[3]提出了基于支持向量机(SVM)技术的油藏预测方法。2005年邢明海等[4]建立了基于模糊神经网络的油田产量预测模型。2009年Weber等[5]通过线性及非线性回归方式表征注入井和生产井间连通性,在此基础上建立了容抗模型(CRM),并通过该模型确定使油藏产出最大化的注水方案。2011年Anifowose[6]回顾了人工智能技术在石油工程中的应用,并总结了人工智能技术在油藏建模及产量管理等方面的用途。2012年Gherabati等[7]将任意注采井在任意地层内的位置作为模型中节点,以此建立神经网络模型,并通过将模拟结果与实际生产数据之间的均方差最小化完成模型拟合。2012年Salazar等[8]通过叠加原理将衰减曲线与容抗模型相结合,对任意生产井的产量进行预测。2013年Holdaway[9]建立了集引导、聚类和数据挖掘于一体的概率模型来进行产量预测。2013年张方舟等[10]将BP神经网络与灰色网络的优点相结合,提出了基于改进灰色网络的产量预测模型。2014年Gupta等[11]提出了基于数据挖掘技术和时间序列分析的产量预测方法。2014年 Zhou等[12]采用多变量回归分析、聚类分析以及主成分分析等数据挖掘技术来识别生产井的产能与地质工程参数的相关性。2016年 Li等[13]以产液剖面及注入剖面数据为目标变量,以渗透率、储集层厚度、注采井距、注入速度和产液量作为影响因素,建立了以支持向量机为核心的多层水驱油藏注水分配模型。2016年Cao等[14]利用地质模型、生产历史数据和生产制度等信息,采用机器学习算法对非常规油气储集层中老井和新井的生产现状进行了预测。2016年赵辉等[15]先将油藏分层离散成一系列由井间传导率和连通体积等参数表征的井间连通单元,再建立针对水驱开发油藏的多层注采井间连通性反演模型,最后给出了相应的模型参数反演方法。2017年Maqui等[16]通过将传统数值模拟方法与纯数据预测方法相结合,将流场转化为适合于最优化方法的注采井网络连接图。2017年武志军[17]基于Spark建立油藏数据处理与分析方法,利用数据挖掘技术对油藏数据进行挖掘,分析油田产量数据与油藏参数之间的关系。2017年Martin等[18]提出了一种采用两步机器学习方案进行产量预测的自动化数据驱动方法。2018年贾虎等[19]基于流线聚类人工智能的方法,开展流场精细化描述,找出潜在优势流场。2019年 Khan等[20]采用人工神经模糊推理系统(ANFIS)和SVM算法建立了一种原油流量估算经验模型,预测人工气举井的产油率。2019年Noshi等[21]探讨了梯度增强树(GBT)、Adaboost和支持向量回归(SVR)3种机器学习算法在产量预测方面的潜在应用。
可以看出,前人主要通过建立预测模型来解决油田生产数据分析预测的问题。然而,井数众多的大型油田往往生产历史较长,井史比较复杂,并且不同井组的流场在不同时刻差异极大,因此有必要建立可对复杂多过程时间序列进行精确预测的模型,以准确表征井组内采出井产油量与注入井注水量之间的关系。本文提出一种基于多变量时间序列(MTS)及向量自回归(VAR)机器学习模型的水驱油藏产量预测方法,在井网分析的基础上通过MTS分析对注采井组数据进行优选,并将井组内不同采出井产油量及注入井注水量作为彼此相关的时间序列,建立VAR模型,从多个时间序列中提取出相互作用规律,挖掘注采井间流量的依赖关系,通过模型拟合来预测生产井产量,并采用不确定性分析及脉冲响应分析方法进行评价。
1 理论基础
1.1 多变量时间序列分析
时间序列是按发生时间顺序排列的具有相同统计指标的一系列值,如果某一变量可以进行时间序列观测,并且过去的数据包含该变量未来变化的信息,则可以使用过去观测数据的某个函数对该变量的未来值进行预测[22]。水驱油藏历史生产数据中就存在时间序列观测数据,如采出井产油量,并且过去的产油量数据包含了未来产油量的变化信息,因此可以利用产油量历史数据去预测采出井未来产油量。在处理历史生产数据变量时,通常一个变量不仅依赖于该变量的过去值,而且还与其他变量在时间上相关。例如,水驱油藏中某一口采出井的产油量变化规律可能还依赖于多口注入井注水量的变化。针对井数众多的水驱油藏的历史生产数据,单变量时间序列分析难以挖掘多口注采井之间的数据关系,因此需要进行多变量时间序列分析。
MTS分析的关键是相关性分析。相关性分析是指对两个或多个变量之间的相互依存关系进行分析,从而衡量变量之间的相关程度及相关方向,挖掘变量之间的内在关系[23]。相关系数是衡量两个变量之间相关程度的指标,其中Pearson相关系数用来衡量两个变量之间的线性相关程度[24]。设有n个关于a和b两个变量的数据对(aq,bq),q=1,2,…,n,则Pearson相关系数的计算公式为:

(1)式中r的取值范围为[-1,1];r的符号表示变量之间的相关方向,r>0表示线性正相关,r<0表示线性负相关;|r|的大小可用来定量分析变量之间的线性相关程度。Pearson线性相关程度评价标准为:|r|=0表示线性无关,0<|r|<0.3表示低度线性相关,0.3≤|r|<0.8表示中度线性相关,0.8≤|r|<1.0表示高度线性相关,|r|=1.0表示完全线性相关。
对于水驱油藏注采井流量而言,可以将不同采出井产油量与注入井注水量作为多变量时间序列,并利用 Pearson相关系数进行相关性分析。依据(1)式可以推导出针对多口注采井流量的 MTS相关性分析公式:

为了增强机器学习模型训练过程的稳定性以及产量预测结果的合理性,可以利用MTS相关性分析结果,对水驱油藏注采井流量数据进行优选。依据Pearson线性相关程度评价标准,并结合(2)式计算的 Pearson相关系数,可以得到如下注采井流量数据优选公式:

(3)式所代表的数据优选过程可以确保某一口采出井(注入井)流量至少与一口注入井(采出井)流量之间存在中度以上的线性相关关系,有利于机器学习模型挖掘注采井间流量的依赖关系。
1.2 向量自回归模型
机器学习模型按照可使用的数据类型分为两大类:监督学习模型和无监督学习模型,其中监督学习模型主要包括用于分类和用于回归的模型。向量自回归模型是一种用于回归的机器学习模型,该模型主要用来处理多变量时间序列数据,通过VAR模型可以挖掘多个时间序列数据之间的相互线性依赖关系。VAR模型是自回归模型与方程联立的结合与延伸,是一种非结构化的多方程回归模型,模型中任意变量均可通过其自身的滞后值、其他相关变量、常数项及误差项组成的方程表示,并可以通过迭代对其未来值进行预测[25]。
注采井间流量的VAR模型并不以油藏工程理论为基础,而是基于注采井流量数据的统计性质来建立。首先将不同采出井产油量与注入井注水量作为彼此相关的时间序列,并构造如下向量:

然后通过注采井间流量的相互关系可以建立如下VAR模型:



其中

最后通过最小二乘法进行求解,总参数矩阵D的最小二乘解ˆD可以表示成如下形式:

对于(5)式给出的 VAR模型,其中重要的参数为滞后阶数p,其代表了假设最多以往p个月的采出井产油量(Yt-1,Yt-2,…,Yt-p)将影响当月采出井产油量Yt。滞后阶数的选择将直接影响到VAR模型的稳定性和准确性,滞后阶数过大会导致估计参数增多,影响模型参数估计的有效性;滞后阶数过小会导致误差项自相关,影响模型参数估计的一致性。滞后阶数一
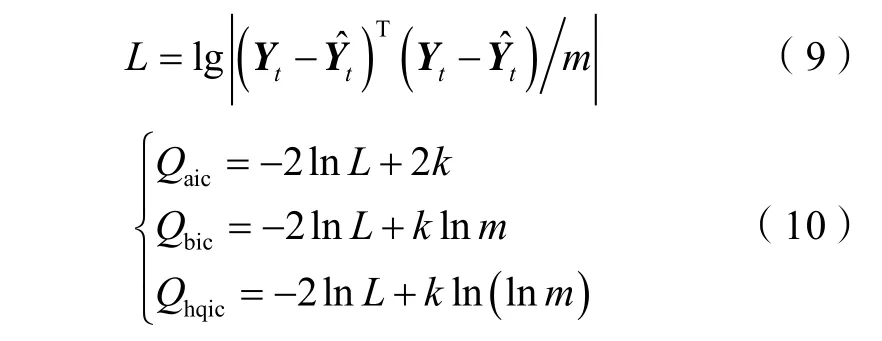
尽管滞后阶数分析可以保证VAR模型的稳定性和准确性,但当给定的数据量较小时,预测结果仍具有一定误差,而不确定性分析可估计以往数据导致的模型误差大小,并给出模型对于预测结果的把握性大小,从而进行更为安全的预测,即在预测不确定性较大时谨慎决策。因此,对模型预测结果进行不确定性分析十分必要。对预测结果不确定性大小的推导主要基于将原本的时间序列过程考虑为随机过程[25],其简洁的矩阵表示如下:

同时考虑到参数的持续影响,未来某一时刻的累计影响矩阵与估计预测误差存在如下关系:

VAR模型不仅可以进行不确定性分析,也可以通过脉冲响应分析对系统进行评价[25],即在模型拟合完成后可通过脉冲响应分析对注入井进行评价,评价依据是将任意注入井日注水量增加固定数值(通常为 1 m3),观察其对整个模型系统影响,注入井的脉冲响应分析公式可以写成如下形式:
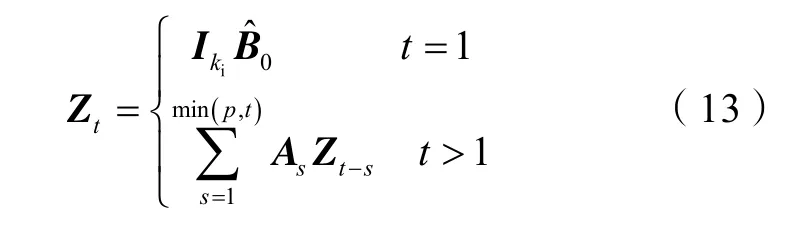
2 模型框架
利用MTS及VAR机器学习模型可以对水驱油藏采出井的产油量进行预测,其模型框架如图 1所示,主要包括以下5个模块。
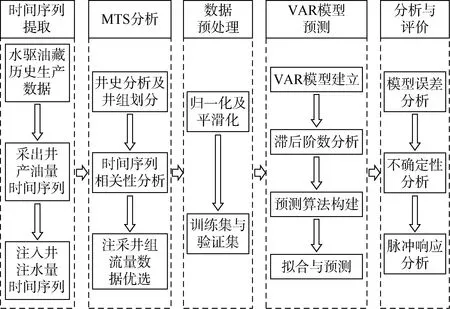
图1 MTS及VAR机器学习模型框架图
①时间序列提取模块。将水驱油藏历史生产数据作为模型的输入,并根据产油量与注水量数据标签以及时间索引提取采出井产油量及注入井注水量时间序列。
②MTS分析模块。在井史分析的基础上进行井组划分,从所有注采井时间序列中截取井组开发时间段内的时间序列,再利用(2)式进行MTS相关性分析,并应用(3)式对注采井组流量数据进行优选。
③数据预处理模块。对优选后的注采井流量数据进行归一化及平滑化处理,增加数据的平稳程度从而降低拟合难度,并将数据划分为训练集与验证集。
④VAR模型预测模块。该模块为模型的核心模块,大致可分为 4个步骤:首先,按照(5)式建立 VAR模型;其次,根据(10)式给出的信息准则进行滞后阶数分析并确定最佳滞后阶数;然后,按照(6)式构建采出井产油量预测算法;最后,利用训练集数据进行VAR模型拟合并预测验证集数据。
⑤分析与评价模块。首先进行VAR模型误差分析,以验证集预测数据与验证集实际数据之间的误差作为评价标准,确保预测结果的准确性,然后利用(12)式进行不确定性分析,提升预测结果的安全性,最后利用(13)式进行脉冲响应分析,进而对注入井的采油贡献量进行评价。
3 实例应用
以国内大港油田某区块的断块油藏作为研究对象,断裂主控区域内共有105口采出井和66口注入井,该区域断层发育,储集层非均质性较强,建立的油藏地质模型共有54个小层,由于油藏地质模型复杂,油藏数值模拟方法收敛性较差,历史拟合比较困难,精度难以保证。本文利用该断块油藏的历史生产数据,根据月度日产油量与日注水量数据标签以及时间索引,提取采出井产油量及注入井注水量时间序列,一共提取了171组数据,每组数据共573个时间样点,时间范围从1970年7月到2018年3月,图2给出了采出井西42-7-3井和注入井西43-67井两口井的历史生产数据。下面在井组分析的基础上,利用 MTS及VAR机器学习模型对该水驱油藏的注采井组流量时间序列进行处理,并对采出井的产油量进行预测与分析,同时对注入井的采油贡献量进行评价。

图2 采出井西42-7-3井与注入井西43-67井的历史生产数据
3.1 MTS相关性分析
在井史分析的基础上进行井组划分,为了降低开发调整与措施对生产数据的影响,同时保证预测结果的可靠性,主要考虑了以下井史:①加密,井组内不增加新井;②调层,主力开发层不调整;③转注,井组开发时间段内所有井不存在转注;④关井,允许短暂的关井。表1给出了井史分析基础上井组划分结果,共选出了10个井组,每个井组的注采井数、主力开发层、开发时间段不尽相同。
利用(2)式对提取出的 10个井组内采出井产油量时间序列与注入井注水量时间序列进行相关性分析,得到注采井组流量时间序列相关图,其中 4个井组的时间序列相关图如图3所示。结合Pearson线性相关程度评价标准,从图3中可以看出,6号井组注采井间流量相关性整体较强,4号和10号井组的注采井间流量相关性整体较差。图4为6号井组中相关性最高的一对注采井的流量时间序列图,其相关系数为0.86,属于高度线性相关,从时间序列图中可以看出注采井流量表现出同增同减的情况。对于4号井组和10号井组,由于两个井组处于断裂带附近,地层中的流体流动规律复杂,因而井组内的注采井间流量相关性整体较差。

图3 注采井组流量时间序列相关图(图中蓝色圆形中的数值为相关系数,圆形的大小代表相关系数绝对值的大小)

图4 6号井组中相关性最高的一对注采井的流量时间序列图
利用(3)式对注采井组数据进行优选,保留相关性较高对应注采井组的数据,表 2给出了注采井组数据优选后的结果。用|Rij|的平均值来表征不同井组的相关性程度,可以发现不同井组的相关性存在一定差异。另外,与表 1中数据对比可知,优选后部分相关性不高的井组将不再进行产量预测分析,如4号井组和10号井组,同时优选后一些井组中部分相关性不高的注采井将不再被考虑,如图3所示1号井组中的采出井西 47-4-2。经注采井组数据优选后便可有针对性地对注采井网系统建立VAR模型。

表1 井史分析基础上井组划分结果

表2 优选后的注采井组数据
3.2 VAR模型拟合与预测
为了保证模型拟合与预测结果的稳定性,对优选后的注采井组流量数据进行归一化及平滑化处理,增加数据的平稳程度,并选取井组开发时间段最后10个月的数据作为验证集,剩下的数据作为训练集。在对数据进行预处理后,对8个井组进行VAR模型拟合与预测,重点讨论整体相关性最高的6号井组结果,图5给出了 6号井组的井位图。进行模型拟合之前,需要先进行滞后阶数分析来确定最佳滞后阶数。利用(9)式和(10)式计算了滞后阶数取不同值时对应的AIC、BIC以及HQIC信息准则评价值。表3给出了6号井组的VAR模型滞后阶数分析结果,可以看出,3种信息准则评价值最小时对应的滞后阶数均为2,因此可以选择2作为最佳滞后阶数。

图5 6号井组的井位图

表3 VAR模型滞后阶数分析结果
最佳滞后阶数确定后,即可开始模型拟合与预测。图6展示了6号井组中西50-5-1井和西50-7-2井两口采出井验证集数据的预测结果,可以看到预测日产量与实际日产量基本吻合,两口井每个产量数据点相对误差的平均值分别为0.036 49和0.012 60,预测数据与实际数据之间的偏差较小,说明了预测结果的准确性。

图6 6号井组中采出井西50-5-1井和西50-7-2井验证集数据的预测结果
分析 6号井组中所有采出井验证集数据的预测情况,并与数值模拟历史拟合结果进行对比分析,结果如表4所示。可以看出,除采出井西51-5-1井的机器学习预测结果较实际结果相对误差较大,其他采出井预测结果的精度都比较高。由图3中6号井组的时间序列相关图分析可知,采出井西51-5-1井与注入井之间的相关性不高,所以对机器学习模型的预测精度有一定影响。对误差较大的采出井西51-5-1井进行不确定性分析,结果如图 7所示,发现虽然该井的预测误差较大,但其预测不确定性范围基本包含了实际数据,确保了预测结果的安全性。

表4 6号井组中所有采出井产量预测结果
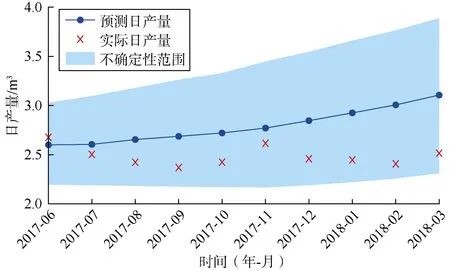
图7 6号井组中采出井西51-5-1井预测结果不确定性分析
对比表 4中机器学习和历史拟合结果可以发现,历史拟合整体相对误差较大,其中采出井西50-5-1井的历史拟合相对误差最大,结合该井的历史拟合曲线(见图8)可以发现,由于油藏模型复杂,开发中期历史拟合精度较高,但开发早期和后期历史拟合较困难,特别是后期历史拟合结果产量有所上升,与实际产量变化有较大差异,因此相对误差较大,相比而言,该井的机器学习结果相对误差非常小,结合该井的机器学习曲线(见图8)可以发现,尽管在历史拟合较困难的开发早期阶段产量数据波动较大,但数据的预处理增加了数据的平稳程度,保证了VAR模型拟合与预测的稳定性;在开发的中后期,产量数据比较稳定,VAR模型能很好地拟合及预测产量的变化趋势,预测效果更好。

图8 6号井组中采出井西50-5-1井产量数据拟合结果
机器学习模型的适应性主要取决于数据的数量和质量两个方面。表5给出了8个井组所有采出井累计产量预测结果,可以发现 3、6、8号井组的相对误差较小,1、9号井组的相对误差较大,结合表1中数据量分析可以发现,数据量的多少对VAR模型的拟合预测精度影响并不显著;相比而言,数据的质量是保证VAR模型可靠性和可用性的关键,结合表2中|Rij|的平均值分析发现,总体而言|Rij|的平均值越大,井组的机器学习模型预测精度越高,说明该参数可以用来评价不同井组机器学习模型的适应性。同时对比1、9号井组|Rij|的平均值发现,虽然9号井组|Rij|的平均值要比1号井组大,但 9号井组的相对误差较大,同时从表 2中发现,9号井组的注采井数明显多于1号井组,说明注采井数也会对井组累计产量预测结果产生一定影响。对比表 5中机器学习和历史拟合结果可以发现,机器学习模型预测结果整体相对误差比历史拟合要小,说明VAR模型对井组累计产量的预测效果更好。

表5 各井组所有采出井累计产量预测结果
3.3 注入井脉冲响应分析
入量增加1 m3,观察其对其他采出井影响,计算公式如(13)式所示。图9展示了6号井组中西50-6井和西50-7井两口注入井对全体采出井采油量影响,例如,影响为0.05 m3代表使全体采出井日采油量共增加0.05 m3,影响为-0.01 m3代表使全体采出井日采油量共减少0.01 m3,以此类推。可见影响量随时间的延续在逐渐减小。图10给出了这两口注入井随时间延续的累计影响,其结果代表一种长期效应,可以看出两口井的累计影响截然相反,说明两口注入井在短期内的驱油潜能存在明显差异。因此可以将2018年3月不同注入井对全体采出井采油量的累计影响作为评价指标来评价注入井的开发潜能,西50-6井、西50-7井、西50-8井这 3口注入井的累计影响分别为 0.916,-0.156,-0.055 m3,可见注入井西50-6井的累计影响较大,说明具有一定的驱油潜能,而西50-7井和西50-8井这两口井的累计影响为负值,说明对所有井的产量产生了一定的负面影响,其中西50-8井累计影响虽然也为负值,但其绝对值很小,说明该井对所有井产量变化的负面影响较小。在实际生产中,方案决策者可以根据注入井脉冲响应分析结果对井组进行注水优化调整,提高水驱油藏的产量。

图9 6号井组中注入井西50-6井和西50-7井对全体采出井采油量影响

图10 6号井组中注入井西50-6井和西50-7井对全体采出井采油量累计影响
4 结语
本文提出了一种基于多变量时间序列及向量自回归机器学习模型的水驱油藏产量预测方法,该方法以井网分析为基础,利用机器学习模型从多个时间序列中提取出相互作用规律,挖掘注采井间流量的依赖关系从而进行产量预测,同时采用脉冲响应分析方法对注入井注水效果进行评价,为进一步注水开发调整提供理论指导。本文方法主观性较少,无需依靠专家经验即可进行评价,且可进行不确定性分析,确保预测结果的安全性与准确性。需要注意的是,对于部分井组,由于地下流体流动规律复杂,机器学习方法并不完全适用,同时部分相关性不是很高的井组的预测结果精度欠佳,因此有必要将其与油藏工程方法相结合来进行综合评价。
符号注释:
a,b——变量;A1,A2,…,Ap——第 1阶,第 2阶,…,第p阶采出井参数矩阵,用于描述不同采出井之间的流量关系;,,…,,——A1,A2,…,Ap,B0的估计值;B0——注入井参数矩阵,用于描述注采井之间的流量关系;c——偏差因子向量;cˆ——c的估计值;ej,t——第j口注入井t时刻的注水量,m3/d;Et——t时刻的注入井注水量向量,m3/d;i,j——采出井和注入井序号;I,P——优选后的注入井和采出井序号集合;——注入井对角单位矩阵;——采出井对角单位矩阵;k——模型参数的个数;ki,kp——注入井和采出井总数;L——似然估计值;m——可观测数据量;Mi——第i口采出井与所有注入井Pearson相关系数绝对值的最大值;Mj——第j口注入井与所有采出井Pearson相关系数绝对值的最大值;n——数据对个数;N——总时间步数;p——滞后阶数,表征最多以往p个月的采出井流量可对现在采出井流量产生影响;q——数据对序号;Qaic——AIC信息准则评价值;Qbic——BIC信息准则评价值;Qhqic——HQ信息准则评价值;r——Pearson相关系数;Rij——第i口采出井产油量与第j口注入井注水量之间的Pearson相关系数;s,t——时间索引;ut——t时刻的残差值向量,=Yt-,m3/d;——平均预测误差矩阵,m3/d;y(h)——未来h时刻的累计影响矩阵,m3/d;yi,t——第i口采出井t时刻的产油量,m3/d;Yt——t时刻的采出井产油量向量,m3/d;Yˆt——Yt的估计值,m3/d;Zt——注入井在未来t时刻的采油贡献量,m3;α,β——优选后的注入井和采出井序号;σi(h)——第i口采出井在未来h时刻的估计预测误差,m3/d;Φt——t时刻的累计影响参数矩阵。
