基于轻量化GANs的引水隧洞充水试验数据生成分析

方卫华 ，张 慧 ，夏童童

（1.水利部南京水利水文自动化研究所，江苏 南京 210012；2.水利部水文水资源监控工程技术研究中心，江苏 南京 210012）

0 引言

随着时间推移，特别是恶劣环境下，监测仪器难免会出现性能降低甚至损坏现象，从而导致实测数据误差加大甚至缺失，而许多数据建模分析方法都对数据样本容量有一定的要求，因此，对缺失数据的有效填充生成一直是数据分析中的重要问题[1]。随着对各种应急条件下现场数据快速分析要求的不断提高，实现现场快速数据生成不仅具有科学研究价值，还具有工程应用价值。

对于缺失数据的传统处理方法主要有多项式值法、近邻值法和样条等插值法，以及矩阵和张量填充、短期预测模型法等，这些方法使用简单，但对外界因素变化适应性差，泛化能力不够，尤其对极端条件下的样本估计不够。现代方法主要包括生成对抗网络（GANs）、玻尔兹曼机、变分自编码器等基于网络的方法，这些方法能有效克服传统方法的不足。相较于玻尔兹曼机等传统模型，GANs 不需要复杂的马尔科夫链的过程，仅需要简单的反向传播过程；与变分自编码器相比，GANs 没有决定性的偏置和变分下界，可以获得更加逼真的结果。因此，相对于传统模型，GANs 训练过程便捷，可以获得更加逼真的结果，是一种比较好的数据生成方法[2]。

GANs 目前主要应用在图像或者视频等高维非结构数据上，这些都需要有较高的硬软件条件[3–9]，现场移动式数据分析设备往往难以满足要求。在水利水电工程现场条件恶劣且无大型设备的情况下，如何解决数据的有效生成问题，目前相关研究和文献不多。为此，以某大型引水隧洞实测数据为样本，研究采用轻量化 GANs 及简易的软硬件设备解决数据生成问题，并采用概率距离测度分析有效性。

1 GANs 模型分析

GANs 由生成器和判别器网络组成，结构如图1所示[10–14]。

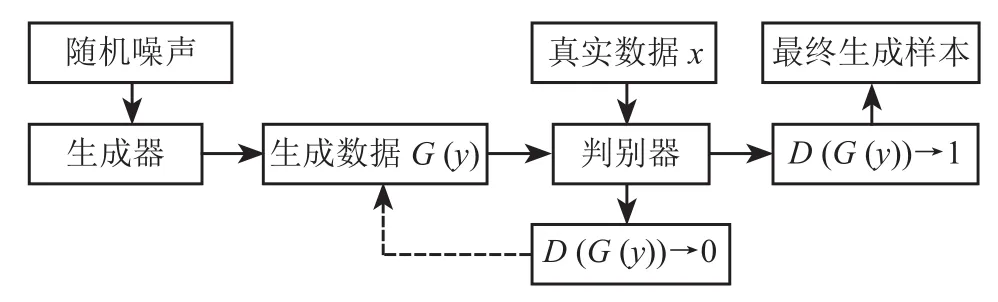
图1 GANs 结构图

用对数损失函数表示目标函数 (V(G，D))，表示为一个极大极小化问题，公式如下：

式中：D(x) 表示判别器输出真实样本的概率；fz(y)为随机噪声的概率分布；fd(x) 为真实样本数据概率分布；D(G(y)) 表示判别器输出生成样本的概率；Ex～fd(x)，Ey～fz(y)分别表示x，y属于某分布时的数学期望算子。

根据测度论中的 Radon-Nikodym 定理，当且仅当生成数据分布等于真实样本数据，即fd(x) =fg(x)，取得全局最优解，这里fg(x) 为x的概率密度函数。当生成器和判别器有足够的学习能力时，通过最优化目标函数，fg将收敛于fd。

GANs 的训练步骤如下：1）固定生成器，最大化值函数V(G，D)，完成对判别器的训练；2）固定判别器，生成器从噪声分布fz(y) 中学习，生成分布为x的数据；3）生成数据G(y) 与真实数据x共同输入到判别器进行数据真伪的判别。在此过程中，生成器的目的是通过不断的循环迭代生成让判别器难以区分真伪的数据，也就是使D(G(y)) = 1；而判别器的目的是尽最大可能地将真实样本数据与生成的假样本数据区分开，也就是使得D(x) = 1 而D(G(y)) = 0。以此循环，直至训练获得理想的数据。

2 网络设计与软件选择

2.1 模型设计

2.1.1 网络层数与节点的选择

考虑到某大型引水隧洞现场数据采集时间短，工况变化快，现场试验训练样本容量不大，模型计算复杂度不能太高，轻量化 GANs 的生成器和判别器网络都选择一个隐含层的 3 层神经网络。

对于输入层和隐含层，其节点数必须小于训练样本数减 1，否则将导致网络无泛化能力；其次，若要得到可靠的网络模型，网络的训练样本数必须要远大于网络连接权的数量。为此，对于输入层，以训练样本的特征数作为节点数目[15–16]。

隐含节点数与输入层和输出层节点数的比例中项属于同一个数量级[17]，因此通过实验模拟给出3 层网络的经验公式：

式中：Ni表示输入层的节点数；No表示输出层的节点数；Nh是隐含节点数。

考虑到本研究分析的数据是一维离散数据，输入层和输出层的节点数都是 5 个，采用式 (2) 计算隐含层节点数大约为 7 个。参照经验公式，在试算的基础上，生成器和判别器网络结构都采用 5×5×5全连接方式，结构如图2 所示。

图2 生成器与判别器网络结构（ y 为输出）

对于生成器，输入 100×5 维的噪声向量，输出也是 100×5 维的向量，其中 100 表示输出的样本量数，5 表示变量个数；网络权重为 5×5 的向量，偏置为 5×1 的向量。

判别器分别对 2 组数据进行训练，一组是生成器输出的数据，另一组是真实数据。判别器的输入是N×5 维的向量，输出是N×5 维的 5 个变量的概率值向量，N表示不定，因为生成数据有100 组，而实测数据为 382 组的训练数据；网络权重也是 5×5的向量，偏置为 5×1 的向量。

2.1.2 激活函数的选择

激活函数的选择直接影响到网络训练结果的好坏。常用的激活函数有 Sigmoid，Tanch，ReLU，Swish 和 Softmax 等函数，根据各激活函数的适用条件、优缺点和使用情况，考虑到 Sigmoid 函数能够抑制误差的传播且应用广泛，对轻量化网络比较适用，因此本研究生成器和判别器的隐含层和输出层的激活函数都采用 Sigmoid 函数，在 Python 软件通过 TensorFlow 自带的 Sigmoid 函数实现。

2.1.3 权重初始化方法的选择

常用的初始化方法有正态分布、Xavier 及 MSRA等初始化方法，由于本研究采用的网络规模较小，因此不考虑 MSRA 初始化方法。通过 Python 软件分别采用正态分布和 Xavier 初始化方式进行训练，标准正态分布和 Xavier 初始化方法训练 1 000 次的训练时间复杂度分别为 4 min 29 s 和 4 min 48 s，训练权重变化分别如图3 和 4 所示。

2 种初始化方法的时间复杂度虽然没有很明显的差异，但从图3 和 4 可以看出，采用标准正态分布初始化训练权重相较于采用 Xavier 初始化训练权重明显是不稳定的，为此权重初始化的方法采用Xavier 初始化方法。

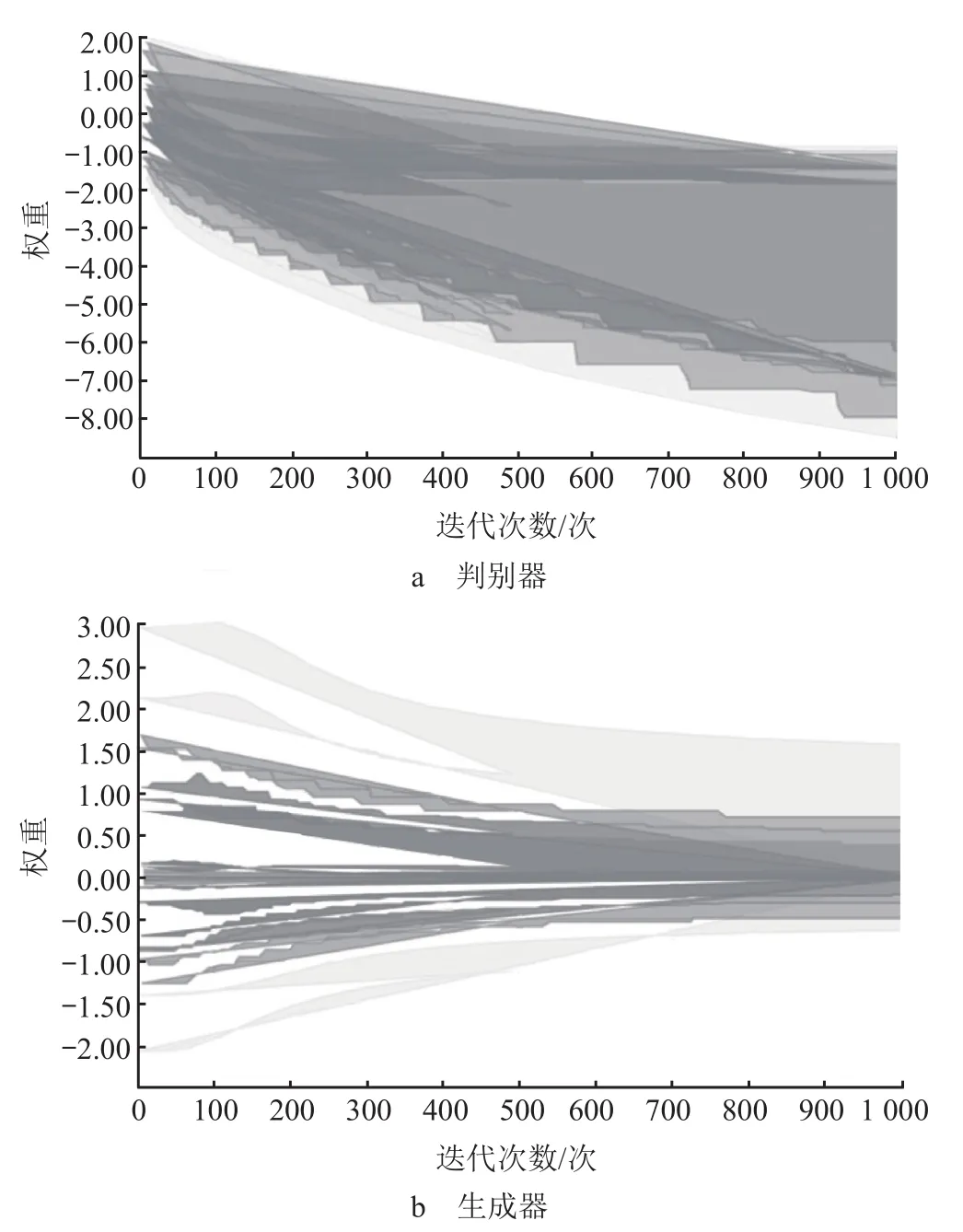
图3 标准正态分布初始化方法训练权重变化

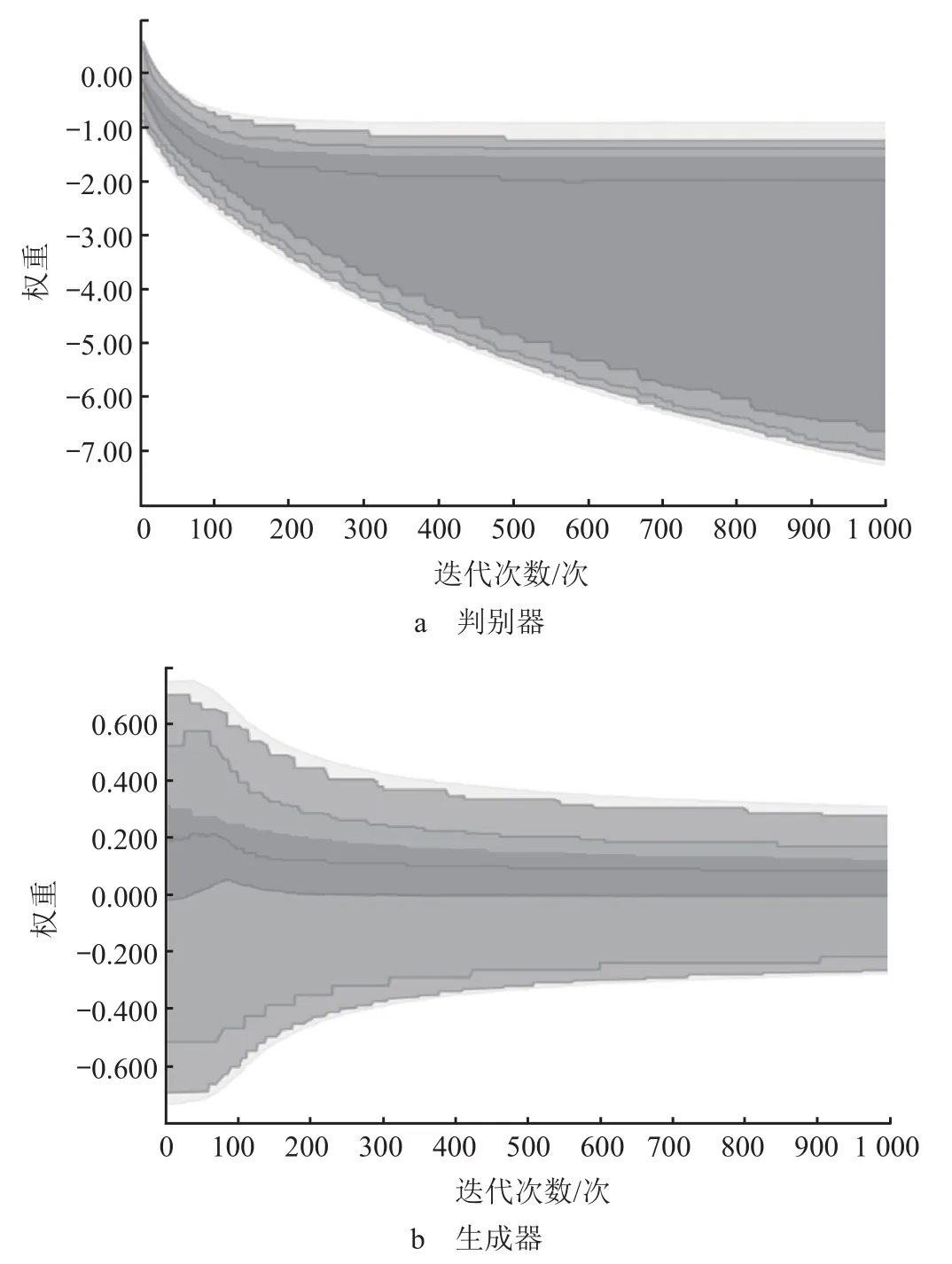
图4 Xavier 初始化方法训练权重变化

2.1.4 损失函数的选择

影响损失函数选择的因素包括网络学习的目标、网络选择的算法、损失函数导数是否容易找到、对网络收敛时间的要求等。根据网络学习目的的不同，可将常用损失函数分为均值平方差和交叉熵 2 类。本研究生成器和判别器的损失函数选择对数损失函数。

2.1.5 参数优化方法的选择

参数优化算法主要有梯度下降法、动量算法和自适应算法三大类，其中梯度下降法应用最为普及。考虑到本研究的数据容量，为避免一次性输入数据导致网络收敛慢及单个输入数据导致优化效果不好，对于参数的优化采用小批量随机梯度优化方法，该优化器可直接通过 TensorFlow 自带的函数实现。网络的训练通过 TensorFlow 的会话计算得到最终结果[18]。

2.1.6 时间复杂度指标的选择

常用 MACCs（乘加操作，实质就是点积运算）计算时间，本研究直接采用训练收敛计算机时间作为衡量网络时间复杂度的指标。

2.1.7 分布间相似性度量的选择

为衡量 2 个样本组分布的相似性，可采用 KL散度、JS 散度和 Wasserstein 距离 3 种基于信息熵的距离公式度量。

采用 KL 或 JS 散度进行概率分布间相似性度量时存在一个问题，即当 2 个概率分布之间完全不相同时，KL 散度值是没有意义的，而 JS 散度值是一个固定不变的常量，即不随着距离的变化而改变。JS 散度本质上是对 KL 散度的改进，在衡量数据分布之间距离上是没有差别的；而 Wasserstein 距离对具有弱关系的 2 个分布也可以有效衡量两者之间的概率距离。因此，采用 KL 散度和 Wasserstein 距离检验数据生成的有效性。

2.2 软件及计算机环境的选择

根据编译和数据分析能力，选择使用 Python 软件完成所有的程序编写和可视化展示，在 TensorFlow学习框架上编程。系统运行硬件平台为笔记本电脑，操作系统为 64 位 Window10 专业版，处理器为Intel (R) Core (TM) i5-4200M CPU @ 2.50 GHz，内存为 4.0 GB。

3 工程实例分析

某引水隧洞为圆形洞，洞径为 7.3 m，设计水压为 0.7 MPa，设计水头为 60 m，隧洞长 99 km。隧洞采用柱塞式充水阀充水，充水阀口径为 500 mm。由于隧洞距离长，采用能进行长距离信号传输的光纤光栅压力式传感器进行水压力监测，共选取 5 个变量进行研究，分别为测值 1（水头波长）、测值 2（温度波长）、水头、温度和水位高程，分别记为x1，x2，x3，x4，x5。采用 2018 年 12 月 28 日 14—22 点间的以 min 为间隔的 482 组隧洞水锤数据作为实测数据样本。

3.1 数据的预处理

3.1.1 数据归一化

由于 5 个测值的单位量纲各不相同，且实测值之间数据量级差异较大（测值 1 的数据基本为1 500 nm 多，而温度只有 3℃ 左右），故首先对数据进行预处理，对 5 组变量分别进行归一化处理。直接通过 Python 软件，用矩阵计算模型 NumPy 进行计算，归一化计算公式如下：

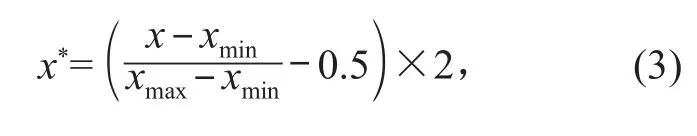
式中：x* 为归一化后数据；xmin，xmax分别为数据的最小值和最大值，数据经过归一化处理后集中在(-1，1) 区间内。

3.1.2 数据分组

将前 382 组数据作为训练集，用于网络训练；后 100 组作为测试集，用于后面的结果检验。

3.1.3 数据读取

CSV 文件作为最通用的一种文件格式，具有存储信息容量小、兼容性高及 Python 处理 CSV 文件更高效等优点，因此原始和生成数据都保存为 CSV文件。采用 Python 软件的 Pandas 库实现对 CSV文件数据的读取与输出，通过 pd.read_csv ( ) 语句实现。

3.2 实验结果的分析

3.2.1 数据流

深度网络的训练过程实质上是一个“黑盒子”，网络训练的结构和过程是无法清楚预知的。在Python 中，充分利用开源库可以简化模型测试、函数调用和输出，由于本模型为轻量化网络，故采用Tensorboard 可视化工具直观展示网络训练过程。在Tensorboard 界面双击矩形节点可以看到详细的训练过程，其中生成器空间包括各层权重和偏置，生成器权重空间包括权重的输入和初始化。

3.2.2 网络收敛性

对于 GANs 收敛情况可采用图示方法显示，通过 Tensorboard 可视化结果，对 382 组样本训练5 000 次，生成器和判别器的损失随着训练次数增加的变化情况如图5 所示。

图5 损失函数收敛过程图

从图5 可以看到：随着网络训练次数的增加，判别器的损失逐渐降低，当网络训练至 3 500 次左右时，判别器损失函数值基本保持在 1.08 上下；生成器的损失随着网络训练次数的增加而不断增加，当网络训练至 3 500 次左右时，生成器损失函数值基本保持在 0.68 上下。此时，网络收敛，网络训练效果较好。

3.2.3 网络时间复杂度

对输入的全部 382 个样本量的 5 个变量训练5 000 次，网络训练时间约为 19 min 30 s。

3.2.4 结果检验

网络训练后最终保存 100 组生成数据，利用这100 组生成数据与 100 组样本测试数据进行结果检验。通过计算 2 组数据的分布间 KL 散度及 Wasserstein距离判断采用的 GANs 训练结果的好坏。

对于 KL 及 JS 散度，首先计算各变量数据的概率分布值（包括 5 个变量各 100 组实测和生成数据），然后用概率分布值计算各变量的 KL 散度值。对于 Wasserstein 距离，不需要计算概率值，直接采用 5 个变量值计算。设定变量各样本数据的权重，从而进行 Wasserstein 距离的计算，本研究采用的数据各样本间不存在差异，因此权重默认为一致。GANs 训练结果检验表如表1 所示。

表1 GANs 训练结果检验表

由表1 可知：5 个变量的 KL 散度值最大值为0.149 7，而 Wasserstein 距离最大值为 2.011 0，2 种方法的计算值表明整体上 5 个变量的生成数据和实测数据之间的差异很小。根据计算结果可以认为采用的 GANs 训练效果很好。

3.2.5 实验对比

为了验证本研究方法的有效性，采用时间序列预测的方法进行分析，并将结果与本研究方法进行对比。对 382 组的训练集进行分析，以变量x1为例，对时间序列建模进行详细分析。

图6 为变量x1的时序图，从图中可以看出：x1明显不平稳，呈现周期性变化趋势。因此，首先对变量x1进行一阶差分，差分后的数据时序图如图7所示。从图7 可知：一阶差分后的x1围绕 0 上下波动，呈现平稳变化趋势。

图6 变量 x1 时间序列图

图7 变量 x1 一阶差分后的时间序列图

然后对变量x1进行 ADF 检验，根据 AIC（赤池信息准则）、BIC（贝叶斯信息准则），模型 ARIMA(2，1，2) 是最优模型。同样的，对变量x2，x3，x4及x5进行分析，最优模型分别为 ARIMA (2，1，4)，ARIMA (5，1，3)，ARIMA (2，1，4) 及 ARIMA (5，1，3)。采用最优模型分别预测各变量的后 100 期的数据。

同样为了检验预测效果，分别采用时间序列预测值和测试集数据计算 KL 散度及 Wasserstein 距离的值，结果如表2 所示。

表2 时间序列分析结果检验表

从表2 可以看出：对于 Wasserstein 距离值，各变量的预测值与训练集数据分布之间的距离不算大，可以说采用时间序列预测效果不算差；对 KL散度值，变量x3的 KL 散度值超过了 1，无解释意义，变量x5的 KL 散度值也高达 0.933 0，而采用GANs 生成的数据与训练集数据计算时，这 2 个变量之间的 KL 散度值都只有 0.080 9[19]，这说明相较于时间序列预测的方法，轻量化 GANs 网络生成的样本更为逼近。

根据 Wasserstein 距离，所提出的轻量化 GANs的数据生成方法的计算结果与时间序列方法的计算结果相比较，5 个变量的数据精确度分别提高了0%，33.3%，1.0%，32.0%，0%，同样说明本研究采用的方法效果更好。

4 结语

很多统计分析方法都对样本数量有一定的要求，对于水利工程现场数据分析而言，由于采样时间、仪器稳定性和数据平稳性等条件限制，许多分析方法难以得到成功应用。以某大型引水隧洞的实测数据为研究对象，采用笔记本电脑，搭建轻量化 GANs，实现了缺失数据的现场便捷生成。概率距离定量分析显示，与时间序列预测方法在生成样本方面相比较，轻量化 GANs 所生成的样本更加逼近真实数据的概率分布。研究表明：本研究方法具有较强的针对性，能在水力学监测和数据分析等高频数据分析中得到应用，对提高数据有效样本数具有一定的实际意义，下一步将把各种作用因素引入 GANs，提升样本生成适应非平稳和变化环境的能力。