巧用定义 数形结合——绝对值的几何意义在最值问题中的应用

赖 倩

（重庆南开两江中学数学组 重庆 401135）

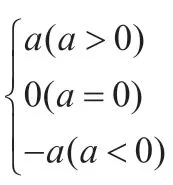
当出现多个绝对值的时候，利用绝对值的代数定义去掉绝对值的“零点分段法”是解决此类问题的主要方法.零点分段法分为找零点，分区间，定符号，去绝对值符号这几个基本步骤，注意有n个绝对值的式子就有n个零点，就会把数轴分成n+1，题目就会分n+1种情况来讨论.

例如：求出满足|2x-4|+|3x+1|=5的x的值.

我们接着来看以下的这个例子：

请回答

（1）若|x-2|+|x+1|=3，则x 能取到的最小值是__________，最大值是___________；

（2）满足|x-2|+|x+1|=2的x有_____个；

（3）满足|x-2|+|x+1|=6的x有_____个，值为_____；

（4）当|x-2|+|x+1|+|x+3|取最小值时，则x的值为__________；

（5）|x-1|+|x-2|+…|x-1 9 9 7|的最小值为____________________.

此题考察的含有绝对值的代数式的最值问题，当然可以用我们前文提到的“零点分段法”来解答，这里就不再赘述.

数轴上表示数a的点与原点的距离叫做数a的绝对值，这既是绝对值的定义又是绝对值的几何意义.数轴上表示数a的点与表示数b的点的距离记作|a-b|，例如|3-5|表示数轴上表示数3的点与表示数5的点的距离，|3+5|=|3-（-5）|表示数轴上表示数3的点与表示数-5的点的距离，|a-3|表示数轴上表示数a的点与表示数3的点的距离.接下来，我们将紧紧抓住绝对值的几何意义，利用数形结合的思想，巧妙的解决这种最值问题.

如本题，当两个绝对值里面x的系数是±1或者说能同时调整为±1的时候，利用绝对值的几何意义，单个绝对值|x-2|可以看做数轴上表示数x的点到2的距离，|x+1|可以看做数轴上表示数x的点到-1的距离，那么整个式子就可以翻译为数轴上表示数x的点到2和到-1两点的距离之和.

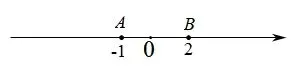
我们利用数轴把题目当中涉及到的数表示出来，利用数形结合，可以看到当点在-1和2之间（即点在图中线段AB上，包含端点）的时候，到两点的距离之和就是这两个定点之间的距离即为AB=|-1-2|=3；当点在线段AB之外（即在-1的左边或者2的右边）的时候，到两点的距离之和就会大于这两个定点之间的距离；并且离这两个点的距离越远，这个值越大.用符号语言来描述上述的结论就是：|X-2|+|X+1|≥3（当且仅当-1≤x≤2时等号成立）.

则此题（1）答案为：若|x-2|+|x+1|=3，则x能取到的最小值是 -1 ，最大值是 2 .

拓展可解决以下问题：满足|x-2|+|x+1|=2的x有_______个；

从前面的分析可以知道，数轴上的点到这两个定点之和的最小值就是这两个定点之间的距离，而本题两个定点之间的距离为3，现在2＜3，∴在数轴上是找不到任何点使得该式子成立的，故答案为0个.

（3）满足|x-2|+|x+1|=6的 有_______个，值为_______；

同前分析，∵6＞3∴在数轴上是找得到这样的点使得该式子成立的.那么这样的点有几个呢？易得，这样的点一定在线段AB之外，我们不妨先来看看当点在-1的左侧的时候，如下图1

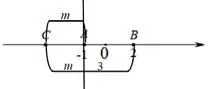
图1

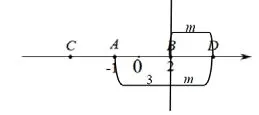
图2

∵2m+3=6 ∴m=1.5 ∴x=-1-1.5=-2.5

而且通过观察可以发现，如图2，当在线段之外与这两个定点的距离相同的点呈现出对称性的性质，即CA=BD时，C、D两点对应的数带入这个式子，到两个定点的距离之和是相等的.∴x=2+1.5=3.5

由此，满足|x-2|+|x+1|=6的x有 2 个，值为 x=-2.5或x=3.5 .

本题的（4）问当|x-2|+|x+1|+|x+3|取最小值时，则x的值为__________；

绝对值增加到了3个，根据前面的分析是数轴上表示x的点到-3，-1，2这三个定点的距离之和.

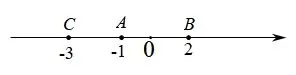
我们知道，x要放在定点的中间，这个距离之和的值就最小，但是此时还有与第三个定点的距离，那放到哪两个定点的中间就需要思考和取舍了，经分析，x要放在最外面的两个定点的中间，即当-3≤x≤2时，x到-3，2这两个定点的距离之和就是这两个定点的距离即为|-3-2|=5，此时还需要考虑|x+1|即与-1的距离，也要尽可能小才行，此时x恰好可以取到-1，使得|x+1|=0，而这个值恰好是绝对值的最小值，两个部分都取到了最小值，而且最小值成立的条件是可以同时成立的，问题得到解决，即|x-2|+|x+1|+|x+3|≥5+0=5（当且仅当 时等号成立）.

可能有同学会思考，x为什么不能放在-3与-1之间或者-1与2之间呢？其实也是可以的，我们不妨以在-3与-1之间为例，当-3≤x≤-1时，|x+1|+|x+3|≥2，那么剩下的第三个绝对值|x-2|在x=-1时，与2最近，|x-2|≥+-1-2+=3，∴|x-2|+|x+1|+|x+3|≥2+3＝5（当且仅当x=-1时等号成立）.

两种方法得到的答案和最小值成立的点都是相同的，但是当绝对值的数量进一步增大的时候，第一种思路会更加方便.

即当|x-2|+|x+1|+|x+3|取最小值时，则x的值为 x=-1 ；

（5）|x-1|+|x-2|+…+|x-1 9 9 7|的最小值为____________________.

这一问的难度就非常大了，一下子拓展到了1997个绝对值的和，乍一看到，很多学生是会无从下手的，需要学生很强的综合能力.但如果学生能充分理解绝对值的几何意义，掌握好前面几个小问的处理方法之后，这个题目也是可以变得相对简单的.整个题目可以翻译为数轴上表示x的点到1，2，…，1997这1997个距离之和.最根本的想法就是让点越往中间走值越小，这1997个数字，有正中间的一个数999，那么当x=999时，整个式子的值最小，最小值为2×（1+2+3+…+998）=997002.

即|x-1|+|x-2|+…+|x-1997|的最小值为 997002 .

这里可以给大家留下几个思考题，参考以上的方法和思路可以得到极大的简化.

补充1：若|b+2|+|a-5|=4-|a-3|-|b+1|，求ab的最大值.

补充2：求|x-2|+2|x+1|+3|x+3|的最小值.

补充3：一条直街上有5栋楼，按从左至右顺序编号为1、2、3、4、5，第k号楼恰好有k（k＝1、2、3、4、5）个A厂的职工，相邻两楼之间的距离为50米.A厂打算在直街上建一车站，为使这5栋楼所有A厂职工去车站所走的路程之和最小，车站应建在距1号楼____米处.

补充4：已知（|x+1|+|x-2|）（|y-2|+|y+1|）（|z-3|+|z+1|）=36，求x+2y+3z的最大值和最小值.

补充5：如图，点O为数轴上的原点，点A、B分别为数轴上两点，对应的数分别为a、b，已知a＝10，AB＝3AO.

（1）若动点P从点O出发，以1个单位长度/秒的速度沿数轴正方向匀速运动，同时动点Q从点B出发以v个单位长度/秒的速度沿数轴负方向匀速运动，经过8秒时，PQ＝16.求v的值；

当然，我们利用绝对值的来表示距离的应用，不仅可以处理距离之和的最值问题，也可以处理距离之差的最值问题，例如：当|x-2|-|x+1|取最大值时，则x的取值范围是____________.

到两个定点的距离之差和到两个定点的距离之和这两种题型之间既有区别又有联系，大家可以利用上述思路去体会一下，同样是可以巧用绝对值的几何意义，数形结合，简化难度，解决题目的.

上文所提到的几个例子由浅入深，层层递进，让我们可以通过这些例子充分体会到绝对值的几何意义在此类最值问题中的重要运用，使用得当可以极大的降低这些最值问题的难度，会让这类学生看起来复杂且无从下手的绝对值相关的最值题目变得简单，希望大家可以在日常教学中充分的讲解绝对值的几何意义，渗透这种数形结合的思想，让学生能够突破难点，掌握此类问题的解题技巧，也能在此过程中体会到定义学习的重要性.