基于遗传算法的分数阶灰色预测模型及其应用

王 安,杨 雨

(1.平顶山学院 数学与统计学院，河南 平顶山 467036；2.平顶山学院 软件学院，河南 平顶山 467036)

0 引言

灰色系统理论是1982年中国学者邓聚龙教授创立的解决“小样本、贫信息”不确定系统问题的新学说[1].吴利丰为了降低模型的扰动，构建了Caputo型分数阶灰色预测模型，并设计了信息优先的规则[2].孟伟建立了分数阶灰色预测模型，并设计了阶数优化的算法[3].惠志昊等人优化了灰色预测模型，并对平顶山市基础教育学龄人口进行预测[4].20世纪国外学者U.Kumar、V.K.Jain使用灰色马尔可夫模型结合了灰色模型和滚动机制以及奇异谱分析(SSA)，预测印度的能源的消耗[5].Chen Zhiqiang等人在能源管理工程采用了灰色GM(1,1)预测模型，为长期预测问题提供更好的预测优势.利用中国能源数据库对改进的GM(1,1)模型的预测性能进行了验证,并与人工神经网络和时间序列的结果进行了比较，实验结果显示明显提高了灰色预测的精度模型[6].Wang Jianzhou等人用多周期Hubbert模型对我国天然气年产量进行了预测,此外，还提出了小样本有效滚动GM(1,1)，实验结果为我国的供需缺口将越来越大[7].分数阶累积GMC(1,1)模型，对原始数据的有效性来优化，该模型能较好地模拟，与传统的灰色预测模型相比，具有显著的预测性能[8].Yang Yang和Xue Dingyu利用分数阶累积法去建立区间灰数的灰色预测模型，与整数阶模型相比，该方法有好的建模和预测性能，可应用于小批量区间历史工业序列样本预测[9].Wei Baolei等人提出了单变量离散灰色多项式模型，并设计了自适应选择模型结构，结果表明了该方法的有效性[10].吴利丰应用最小二乘法的摄动理论解释了累积生成算子违背了灰色新信息优先原则系统论，提出了一种新的分数阶累积灰色系统模型，实例计算结果与传统的预测方法相比，具有非常显著的预测性能[11].Mao Shuhua等人认为经典的GM(1，1)模型有以下缺点：它不能反映新的信息优先原则，如果是为了获得理想的建模效果，原始数据必须满足比率要求[12].王安等人先后设计了灰色组合优化模型[13-14]，以及一类新的灰色耦合模型[15]，并通过算例证明了其有效性.

在大量的数据中，如何提取有价值的数据，利用高质量的数据，构建高效的数学模型已成为当今研究的重要课题，笔者提出了一种基于遗传算法的分数阶灰色预测模型，该方法是提高模型精度，拓展模型的应用范围的一种尝试，通过算例验证了该模型的有效性.

1 模型的建立与检验

分数阶灰色预测模型是利用数据建立分数阶预测模型，然后设计阶数优化的动态模型，先把原始数据序列进行分数阶累加，然后对分数阶累加逐个累加.根据分数阶累加序列进行建模，最后对阶数进行优化，使得分数阶灰色预测模型精度得到提高.具体的分数阶预测模型的建立过程如下：

定义1[3]令X(0)={x(0)(1),x(0)(2),…,x(0)(n)}为原始数据,对X(0)进行分数阶累加，r∈R+,X(r)=(x(r)(1),x(r)(2),…,x(r)(n))是X(0)=(x(0)(1),x(0)(2),…,x(0)(n))的r阶累加生成序列，其中，

k=1,2,…,n.

称xr-1(k)+az(r)(k)=b为分数阶灰色预测模型，其中:

(1)

分数阶灰色预测模型x(r-1)(k)+az(r)(k)=b的时间响应序列为:

k=2,3,…,n.

(2)

还原值为:

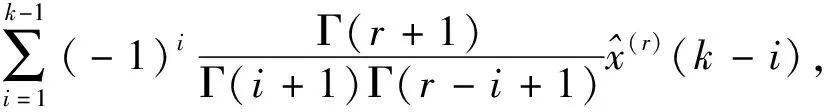
k=2,3,…,n.

(3)

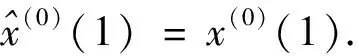
根据分数阶灰色预测模型的原理，算法步骤可概括如下：

步骤1 生成r阶累加序列和r阶累减序列

设X(0)=(x(0)(1),x(0)(2),…,x(0)(n)),r∈R+,X(r)=(x(r)(1),x(r)(2),…,x(r)(n))是X(0)=(x(0)(1),x(0)(2),…,x(0)(n))的r阶累加生成序列，其中:

k=1,2,…,n.

其中:

X(-r)=(x(-r)(1),x(-r)(2),…,x(-r)(n))为X(0)的r阶累减生成算子，其中:

x(-r)(k)=

k=1,2,…,n.

步骤2 建立一阶微分方程

其为分数阶算子GM(1,1)模型白化微分方程.

步骤4 求出分数阶GM(1,1)的时间响应式

k=2,3,…,n.

步骤5 将数值进行r阶次累减还原，得到预测值.

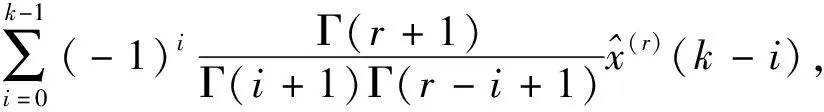
k=2,3,…,n.

步骤6 模型检验

残差检验公式为:

(4)

相对误差检验公式为:

(5)

其中,平均绝对百分比误差检验公式为:

(6)

基于遗传算法的分数阶灰色预测模型阶数优化的算法流程图见图1.

图1 基于遗传算法的分数阶灰色预测模型阶数优化的算法流程

2 算例分析

根据河南省统计年鉴中2000—2017年河南省的能源消费数据，利用构建的基于遗传算法优化的分数阶灰色预测模型和经典的灰色预测模型进行对比，见表1.利用遗传算法，进行全局搜索最优解，在迭代了20代后，得到阶数为r=0.727 15时是最优解，如图2和图3，与上述之前的误差进行对比,见表2.

表1 5个模型的河南省能源需求量的预测结果 万t

图2 分数阶灰色预测模型基于遗传算法阶数r进化过程

图3 分数阶GM(1,1)阶数优化的相对误差总和进化过程

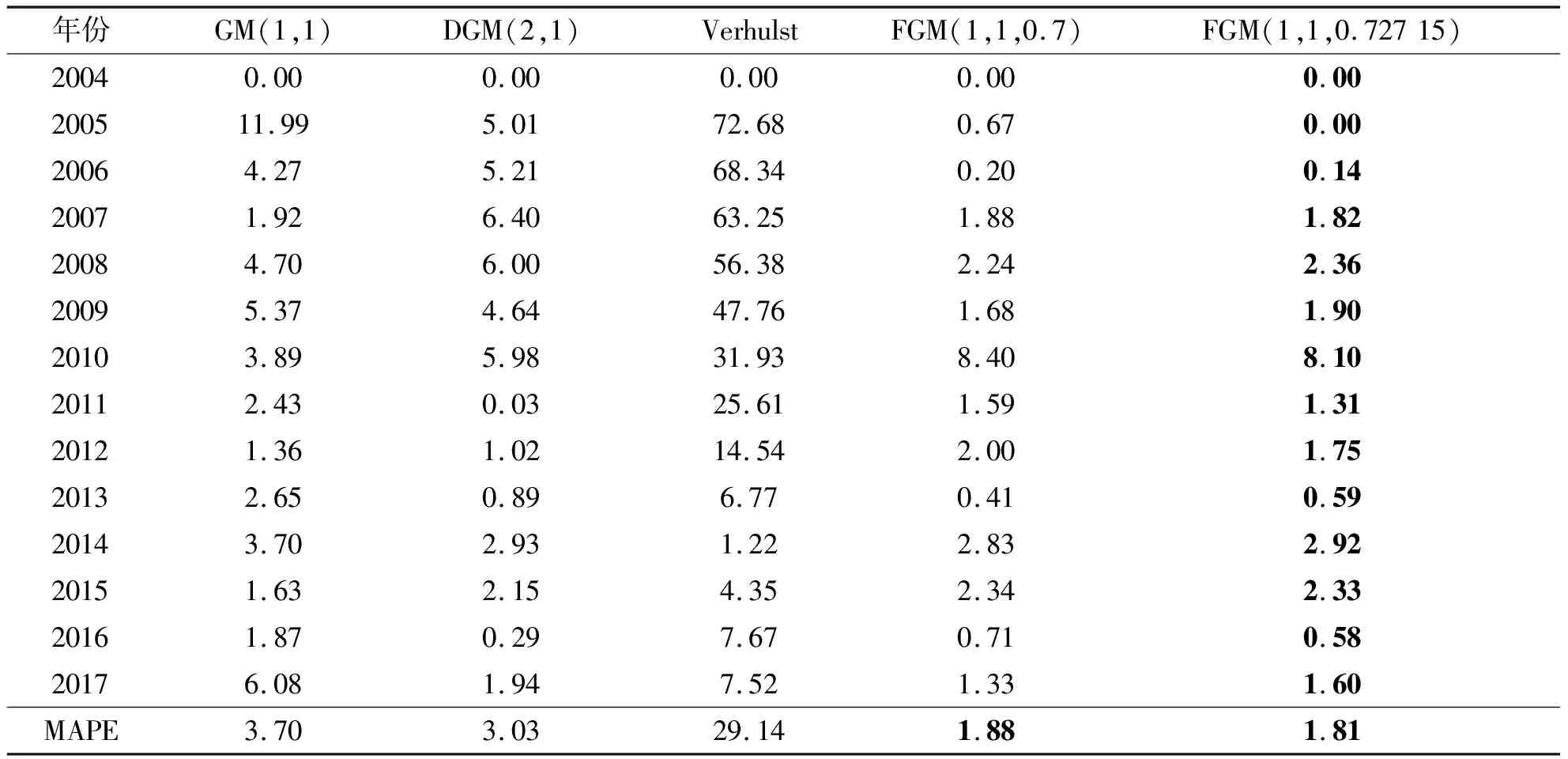
表2 5个模型的河南省能源需求量的相对误差对比

研究结论如下：根据2004—2017年的河南省能源消耗量数据，进行建模仿真，利用遗传算法在全局寻找最优近似解r=0.727 15之后，精度相比之前在单位0.1递增去尝试分数阶灰色预测模型的最好阶数为r=0.7时提高了0.07%的精度，利用遗传算法能够快速准确地解决分数阶灰色预测模型阶数的优化问题.

最优分数阶灰色预测模型与其他灰色预测模型相比较平均相对误差为1.81%最小,预测的模拟精度最高.利用最优分数阶灰色预测模型对河南省未来8年能源需求量进行预测.预测结果见图4和表3.

图4 河南省未来8年能源需求量的预测

表3 河南省未来8年的能源需求量的预测值 万t

从图4和表3可以看出，2018—2025年河南省的能源需求量呈现上升的趋势，分别为23 610.21、23 883.87、24 134.48、24 364.33、24 575.35、24 769.23、24 947.42、25 111.21.

3 结论

构建了基于遗传算法的分数阶灰色优化模型.通过算例发现:相对已有的灰色预测模型，分数阶灰色优化模型的预测结果精度更高.

分数阶灰色优化模型从灰色预测模型的白化方程出发，将GM(1,1)模型的阶数1推广到阶数r，并且对阶数r用遗传算法进行优化，利用优化后的阶数进行预测，精度得到了明显提升.因此,针对不同的分数阶灰色预测模型阶数r的优化，以及分数阶灰色模型的建模机制的改进等问题，值得进一步研究.